基于改进型预估FOPID 的选择性激光烧结预热温度控制研究＊

崔 昊 郭艳玲 肖亚宁 蒋成雷 李 健 王扬威

（东北林业大学机电工程学院，黑龙江 哈尔滨 150040）

选择性激光烧结技术是一种得到广泛应用的增材制造技术[1]。在该工艺加工过程中，存在一个名为预热的关键环节。预热过程对成型件的加工质量以及力学性能有着明显的影响。目前多采用传统比例-积分-微分（PID）控制器来进行预热温度控制，由于被控对象具有纯滞后特性，控制系统时常会出现响应速度慢、超调量过大等现象，无法将工作面温度加热到目标温度并维持恒定，进而影响成型效果[2]。因此，提出一种更加有效的控温策略是有必要的。由于传统整数阶控制器对某些系统已达不到控制要求，因此人们越来越重视分数阶控制领域[3]。分数阶PID 控制器（FOPID）由Podlubny I[4]提出，为分数阶控制理论与PID 控制器的结合。FOPID 相对于整数阶PID 控制器多了积分和微分阶次，从而在控制精度和范围理论上较后者都会有很大的改善，并且FOPID 控制器具有更好的灵活性、适应性和鲁棒性[5]。

元启发式算法源于自然界中的随机现象[6]。阿奎拉优化器（AO）便是其中的一种范式。它由Abualigah L 等[7]于2021 年提出，模仿了阿奎拉的狩猎行为，是一种新型的智能优化算法，尽管标准AO 算法已经具有良好的性能表现，但由于优化问题的复杂度日益增加，其也时常会暴露出探索和开发不平衡，陷入局部最优等缺陷。为此，一些人尝试通过在AO 当中引入改进策略来获得增强型算法。例如，Yu H J 等[8]开发出一种名为mAO 的增强型算法，并通过测试验证了其具有一定优越性和有效性；Zhao J 等[9]删除了AO 的开发阶段，提出了一种名为IAO 的简化AO 算法。上述文献都对AO 的缺陷进行了不同程度的改进。目前，一些元启发算法已经应用在分数阶控制器的参数整定问题中。黄丽莲等[10]开发了一种自适应差分进化算法并将其应用于分数阶PID 的参数整定问题中；陈炫儒等[5]开发了一种改进麻雀搜索算法，并将其应用于分数阶PID 的参数整定，获得了较为优越的控制效果。上述应用都取得了一定成果。

本文在经典FOPID 控制器当中引入了Smith 预估器以消除纯时滞环节产生的震荡，提高被控系统的鲁棒性；为克服AO 在探索和开发阶段的不平衡以及易于陷入局部最优的缺陷，引入了白冠鸡优化算法中的领导者更新机制，自适应切换系数以及折射反向学习策略，提出了一种名为EAOCBO 的增强型混合阿奎拉优化器，并将其用于对Smith 预估FOPID 控制器的模型参数进行最优设计。采用IEEE CEC2017 基准函数对EAOCBO 进行了性能对比测试，证明了其具有更加优秀的性能。通过仿真软件分析了所提出控制器在单位阶跃信号下的动态响应特性，并将其应用于烧结样机预热温度控制当中，开展成型效果试验。结果证明所提控制方法具有出色的响应速度和控制精度，并且在实际应用中也能精确地控制温度，改善预热温度场的均匀性，进而提高成型件的尺寸精度。

1 改进阿奎拉优化器

1.1 阿奎拉优化器

AO 是一种新颖的仿生智能算法[7]，它模仿了阿奎拉鸟的智能狩猎策略包括：①垂直俯冲的高空翱翔；②短滑翔的等高线飞行；③缓慢下降的低空飞行；④降落并近距离攻击。前两个策略为探索阶段，后两个为开发阶段。算法每个阶段的执行条件为：如果t≤(2/3)T，则执行探索步骤；否则，将执行开发步骤，其中t为当前迭代次数，T为最大迭代次数。在优化迭代前，需对所有个体位置进行初始化：

式中：Xi为种群中第i个搜索代理的位置；rand为(0,1)的随机数；UB为搜索空间的上边界；LB为搜索空间的下边界；N为种群大小。

在第一种捕食策略中，阿奎拉的位置更新公式为

式中：Xi(t+1)为第i只个体在第t+1次迭代的侯选位置；Xbest(t)为目前获得的最优解；r1为(0,1)的随机数；Xm(t)为种群的平均位置，计算公式如下：

第二种捕食策略中，阿奎拉的位置更新公式表示为

式中：Xr(t)为随机选取的一个阿奎拉个体的位置；D为问题维度；r2为(0,1) 的随机数；LF(·)为Levy飞行分布函数。

在第三种捕食策略中，阿奎拉的位置更新公式为

式中： α和 δ均为开发调整系数，等于0.1；r3和r4为(0,1)的随机数。

在第四种捕食策略中，阿奎拉的位置更新公式为

式中：QF为用于平衡搜索策略的质量函数；G1为运动参数，是(-1, 1)的随机数；G2为阿奎拉的飞行斜率，其大小是(0, 2)的线性递减；r5、r6、r7、r8都是(0, 1)的随机数。

1.2 领导者机制

白冠鸡优化算法（CBO）是Naruei I 等[11]在2021 年提出的一种无梯度优化方法。在CBO 中，跟随者向领导者靠近的同时，领导者也会不断靠近最优区域，有时领导者必须离开当前最佳位置，才能找到更好的位置，从而提高算法跳出局部最优解的概率。领导者的位置更新公式如下：

式中：gbest为种群内最优个体的位置；R1和R3为[0,1]区间的随机数；R2为[-1,1]的随机数；B的计算公式如下：

1.3 自适应切换系数

在本文中，采用自适应切换系数E来替代原始AO 算法中的探索—开发阶段执行条件（判断当前迭代次数和最大迭代次数是否满足t≤(2/3)T），更好地平衡其探索和开发能力[12]，其定义如下：

式中：r为(0,1)的随机数；当E>1时，算法进行探索阶段，当E≤1时则执行开发阶段。为研究算法不同阶段的转换概率，令θ=2(1-t/T)，则E>1时概率的计算公式如下：

由式（11）可知，在迭代过程当中，算法进行探索与开发阶段的概率大致相同，有利于平衡两者之间的切换，进而增强算法的搜索性能。

1.4 折射反向学习

折射反向学习[13]（ROBL）是在反向学习的基础上引进光线折射原理来生成反向候选解，其数学表达式如下：

式中：Xi,j为当前第i个个体的位置在第j维上的分量；为Xi,j对应的反向解；aj和bj分别为搜索空间中第j维的下限值和上限值；k为比例因子；n为折射率。

1.5 EAOCBO 优化算法

AO 算法存在迭代后期种群多样性低，局部探索能力不足，容易陷入局部最优等缺点。为了全方面提高AO 算法的优化性能，本文尝试将CBO 的领导者机制，自适应切换因子以及ROBL 策略融入到AO 当中。

首先，利用CBO 的领导者机制更新AO 初始化种群位置，当种群位置利用领导者机制更新公式计算完后，评估新一代个体位置与原位置的适应度值，保留取优值参与改进算法之后的迭代计算。新的位置更新公式如下：

其次，通过折射反向学习在每次迭代前对种群位置进行更新，同时评估当前位置解和反向解以提高获得全局最优解的概率，避免陷入局部最优，可以有效增强算法的开发阶段。最后，本文采用自适应切换系数E来替代原始AO 中的执行条件，更好地平衡算法的探索和开发能力，增强算法的性能。EAOCBO 的具体实现步骤如下。

步骤1：初始化算法各参数，利用公式（1）随机初始化种群位置。

步骤2：利用公式（13）更新当前种群位置，计算并比较适应度。

步骤3：若切换因子E＞1 且rand≤0.5，则通过公式（2）更新当前种群位置，计算并比较适应度。

步骤4：若切换因子E＞1 且rand＞0.5，则通过公式（4）更新当前种群位置，计算并比较适应度。

步骤5：若切换因子E≤1 且rand≤0.5，则通过公式（5）更新当前种群位置，计算并比较适应度。

步骤6：若切换因子E≤1 且rand＞0.5，则通过公式（6）更新当前种群位置，计算并比较适应度。

步骤7：通过公式（12）计算反向解Xi，评估其适应度值并与对应当前解进行比较。

步骤8：判断迭代次数t是否达到最大迭代次数，若是，则输出全局最优解，否则返回步骤3 循环执行。

2 预估FOPID 控制器设计

FOPID 控制器为分数阶控制理论与PID 控制器的结合，其一般格式简记为PIλDµ[14]。与传统PID控制器相比，其控制的精度和范围理论上都较整数阶PID 控制器来说会有很大的改善。分数阶PID 控制器的数学表达式如下：

式中：Kp为比例增益调节系数；Ki为积分时间系数；Kd为微分时间系数； λ为积分阶次； µ为微分阶次；r(t)为t时刻系统的输入量；y(t)为系统实际输出量；e(t)为系统偏差量；u(t)为控制器的输出量。

在工业过程控制系统中，被控对象难免会存在滞后现象。具有纯滞后环节的控制系统，当外界扰动发生后会严重损害控制系统的稳定性，甚至导致系统无法工作。Smith 预估器由美国加利福尼亚大学Smith O J M[15]提出，该方法的控制思想是：针对具有滞后环节的被控对象，评估其动态特性并构建补偿环节，将滞后环节的被控量超前反馈到调节器，使得调节器提前动作以达到减小系统超调量的目的。Smith 预估器的原理如图1 所示。

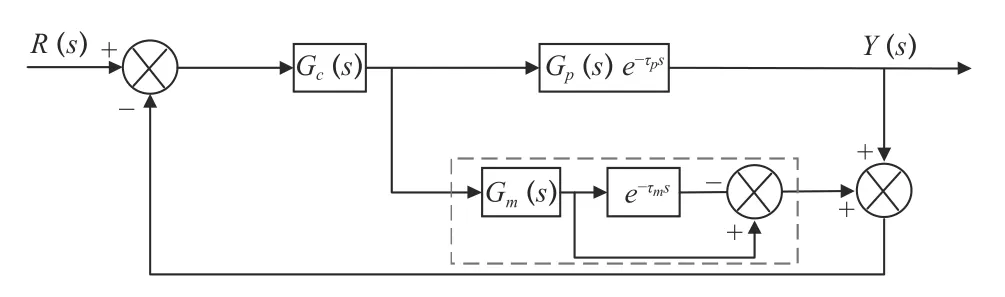
图1 Smith 预估器的结构框图

FOPID 控制器具有5 个可调参数。选择合理的参数组合，可以使控制器获得更理想的控制效果，有效提高系统性能，但控制器设计的复杂性也相应增加。本文利用EAOCBO 来实现对FOPID 控制器的5 个关键参数进行优化自整定，选择误差积分准则（ITAE）作为控制器的性能评价指标，其计算公式如下：

式中：t为时间。利用EAOCBO 进行Smith 预估FOPID 参数整定过程可以简化为一个优化问题。FOPID 的参数组合是EAOCBO 求解的位置向量，而ITAE 是适应度函数。算法的求解过程则为整定{Kp,Ki,Kd,λ,µ}这5 个参数使得适应度函数值达到最低，即EAOCBO 在五维空间Xi={Xi1,Xi2,Xi3,Xi4,Xi5}中寻找最优解。EAOCBO-Smith 预估FOPID 控制器的结构如图2 所示。

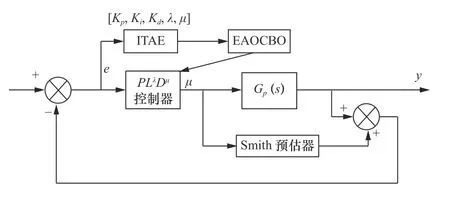
图2 EAOCBO-Smith 预估FOPID 控制器的结构框图

3 仿真案例分析

在本节中，对提出的改进算法以及控制器的性能进行了评估。所有试验均在Windows 10 操作系统上进行，计算机硬件配置为Intel(R) Core(TM) i5-7300HQ CPU@2.50 GHz 和8GB RAM，软件环境为Matlab 2020b。

3.1 基于IEEE CEC2017 基准函数的性能测试

为验证EAOCBO 在解决复杂数值优化问题层面的有效性，本文使用IEEE CEC2017 测试集中的9 个代表性基准函数[16]来测试EAOCBO 的性能。选用了5 种先进的算法进行比较，分别是AO、正余弦算法（SCA）[17]、算术优化算法（AOA）[18]、鼠群优化器（RSO）[19]和黄金正弦优化算法（Gold-SA）[20]。算法的所有参数设置均与原文保持一致。本文采用平均适配度（Mean）和标准偏差（Std）评价指标来评价算法性能。各算法种群大小设置为50，迭代次数为500。所有算法都独立运行了30 次，结果见表1。EAOCBO 可以获得更好的平均适应度值，同时具有更好的标准差，充分说明本文提出的EAOCBO 具有更加优秀求解进度、求解速度和稳定性。测试函数收敛曲线如图3 所示，可以看出，EAOCBO 具有十分明显的收敛优势。在所有函数当中，EAOCBO 都可以在早期搜索阶段保持着很高的收敛速度，这得益于引入的CBO 的领导者机制可以充分利用解空间中的信息，提高了EAOCBO 的种群多样性和全局探索能力。而在后期迭代过程中，EAOCBO 同样可以保持较好的收敛趋势，这得益于折射反向学习的引入，提高了算法跳出局部最优的可能性。而自适应切换系数为算法提供了更好的探索和开发之间的平衡关系。上述结果充分验证了EAOCBO 的有效性和优越性。

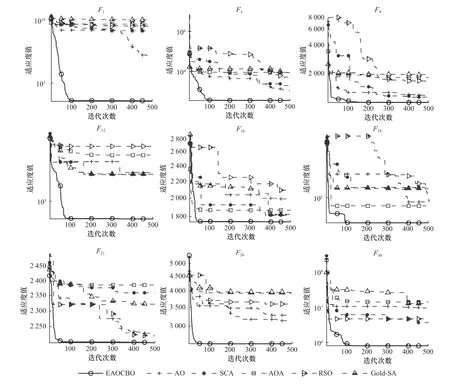
图3 不同对比算法在IEEE CEC2017 基准测试函数上的收敛图

3.2 控制器性能测试

为验证本文所设计的EAOCBO-Smith 预估FOPID 控制器的有效性，本文选取了一个经典被控系统进行验证并与已有控制器进行了对比分析。以典型二阶被控系统为例，传递函数为

采用几种已有文献中的控制器进行对比，黄丽莲等[10]采用改进差分进化算法优化的PID（C1）和FOPID（C2）、陈超波等[21]提出ABC-FOPID控制器（C3）、陈炫儒等[5]提出ISSA-FOPID（C4）以及本文设计的控制器用C5表示。原始文献中4 种算法在解决式（17）对应的传递函数时，参数设置如下：

在EAOCBO 算法中设置5 个参数搜索范围取为Kp,Ki,Kd∈[0,200] ，λ,µ∈[0,2]。由于本例中传递函数中不存在滞后环节，因此控制器中延时时间设置为0，通过算法整定后获得的最佳参数组合为{192.7168,9.2333,44.9397,0.9985,0.9087}。仿真得到的响应曲线如图4 所示，性能指标见表2。从响应曲线以及表中数据可以看出，本文设计的控制器相比于C1，其上升时间，峰值时间以及调节时间都明显缩小，稳态误差减少了0.001，超调量略差于C1；相比于C2，虽然在上升时间，峰值时间以及超调量方面略差，但调节时间缩短了0.384 s，稳态误差减少了0.004；相比于C3，其上升时间，峰值时间以及调节时间都明显缩短，超调量缩短了8.22%，稳态误差减少了0.008；相比于C4，虽然在上升时间，峰值时间方面略差，但调节时间减少了0.068，超调量减少了5.4%，稳态误差减少了0.002。这说明提出的控制器可以获得更加稳定的结果，综上所述，提出的EAOCBO-Smith 预估分数阶PID 控制器具有更好具有优秀的快速性、稳定性、准确性。

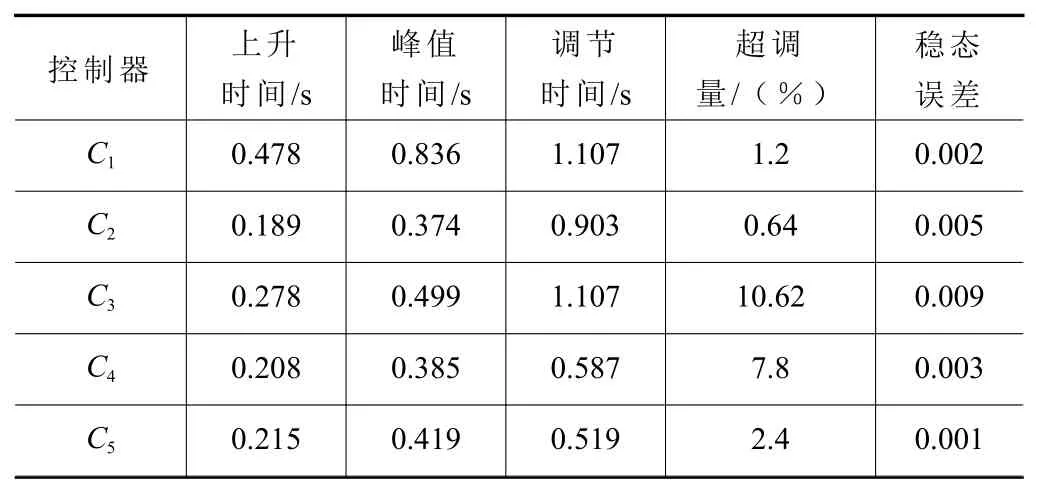
表2 不同控制器的性能参数指标

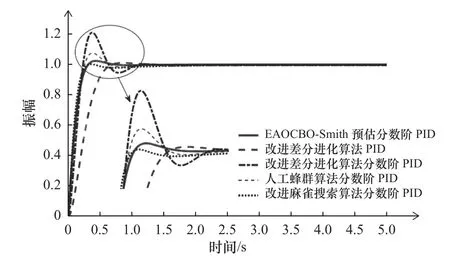
图4 不同控制器的响应曲线对比图

4 应用环境

本节以哈尔滨自由智造科技开发有限公司生产的CX-B200 激光烧结成型机管式预热装置为研究对象，CX-B200 激光烧结成型机如图5 所示，管式预热装置如图6 所示。在该装置中，4 根完全相同的加热管呈中心对称分布安装在粉床正上方以对烧结粉末进行预热。在控制过程中，由于测量元件的时间滞后以及电热丝热惯性，使得控制信号与温度测量值之间存在着一个时滞环节e-τs。在实际应用中，当输入电压为3 V 时，温度稳定在60 ℃，因此放大系数K=60/3=20 ℃/V。输入信号经控制器运算输出整个过程耗时约1 s，因此延时时间τ=1。本文仿真对象的具体数学模型如下：

图5 CX-B200 烧结设备

图6 管式预热装置

通常，对于不同的加工材料会设定不同的预热温度，为探究控制器在变温度条件下的响应输出，设定初始预热温度T=80 ℃，在时间t=15 s 时，温度下降至T=50 ℃；在时间t=30 s 时，温度上升至T=90 ℃，总仿真时间为50 s。在Matlab 环境中搭建SLS 铺粉预热装置温度控制系统的Simulink 模型并进行仿真，仿真曲线如图7 所示，可以看出，当温度产生变化时，本文设计的控制器可以快速响应，在短时间内达到稳定状态，说明提出的控制器能够很好地控制温度，能够适应不同打印材料切换所面临的复杂变温情况，而且可以快速恢复稳定状态，有助于提升打印效率。

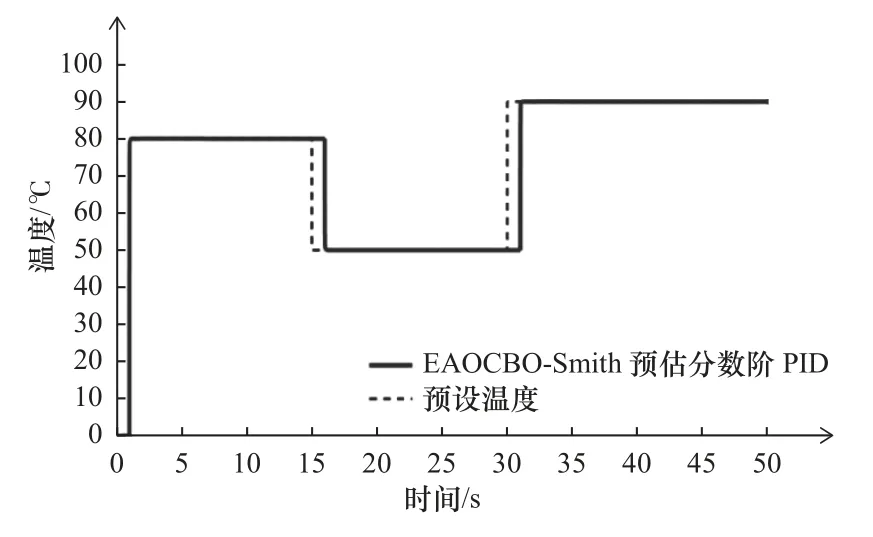
图7 变温条件下控制器的响应曲线

然后，对所提出控制器的实际控制效果进行验证。由于加热元件的布置是对称的，因此可知粉床在受热的过程中温度的分布也是对称的。为精确地了解粉床表面的温度分布，试验中选择粉床的1/4的区域作为主要研究对象，如图8 所示，并增加了12 个特殊点以使区域内部温度分布的情况更加的细化。

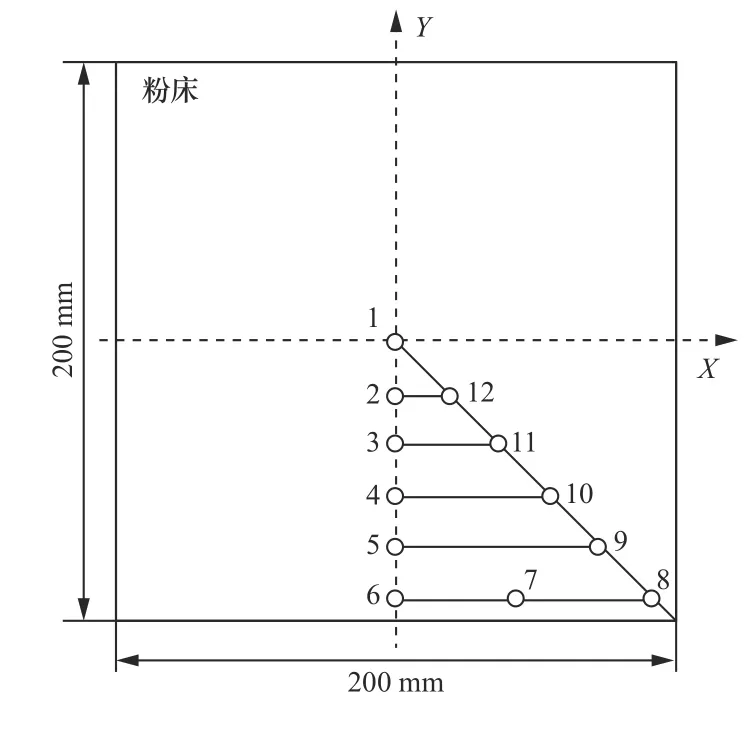
图8 温度采样点的位置分布图

利用聚醚砜（PES）粉末材料进行试验，设定预热温度为85 ℃，环境初始温度为25 ℃，本文选择型号为STM32F407VET6 的芯片作为温度控制系统的主控芯片，温度测量采用SA20BH 非接触式红外温度传感器，将提出的EAOCBO-Smith 预估FOPID 控制器以及当前采用的传统PID 控制器移植到STM32 开发板上，分别使用两者对温度进行控制。为减小外部环境因素引起的突变性扰动导致采集的信号产生尖锐脉冲干扰，采用中值滤波处理原始温度数据。中位滤波是一种典型的非线性滤波器，它运算简单，在滤除脉冲噪声的同时能够很好地保护信号的细节特征。主要操作思路为每个采样点连续采样30 次，各采样点的30 个温度数据经过中值滤波处理后获得的数据为真实采样值。在温度达到稳定状态时，中值滤波处理后各采样点的温度结果如图9 所示。由图9 可知，当采用本文设计的控制器进行温度控制时，粉床不同区域温度梯度变化较小，相较于PID 控制算法更平稳。例如，采样点4、7 两处采用PID 控制算法时，温度差约4.8 ℃；而使用本文设计的控制器时，温差约为1.2 ℃，并且本文设计的控制器总体能获得与设定值偏差更小的温度值。这充分说明了本文设计的控制器具有优秀的控制效果。此外，为验证所设计的预热温度控制系统是否能够提高成型精度，本文还进行了烧结成型试验，打印模型如图10 所示。针对传统PID 控制器和本文设计的FOPID 控制器在相同参数设置下共进行6 次烧结试验，每次同时打印3 个模型，烧结过程如图11 所示，部分成型件实物图如图12所示，使用游标卡尺进行测量，如图13 所示，各成型件在X、Y、Z方向上的收缩率记录见表3。从表3 中数据可以看出，相较于传统PID 控制器，本文设计的控制器可以更有效地控制温度，进而使得成型件收缩率明显减小，PID 控制器的 εx、 εy、εz分别为1.318%、7.55%、6%，EAOCBO-Smith 预估FOPID 控制器的 εx、 εy、 εz分别为1.125%、5.925%、2.416%。相较于传统PID 器，EAOCBO-Smith 预估FOPID 控制器控制下成型件的 εx、 εy、 εz分别减少了0.193%、1.625%、3.584%，意味着该方法可以有效减少出现收缩变形等缺陷，进一步提高成型精度。

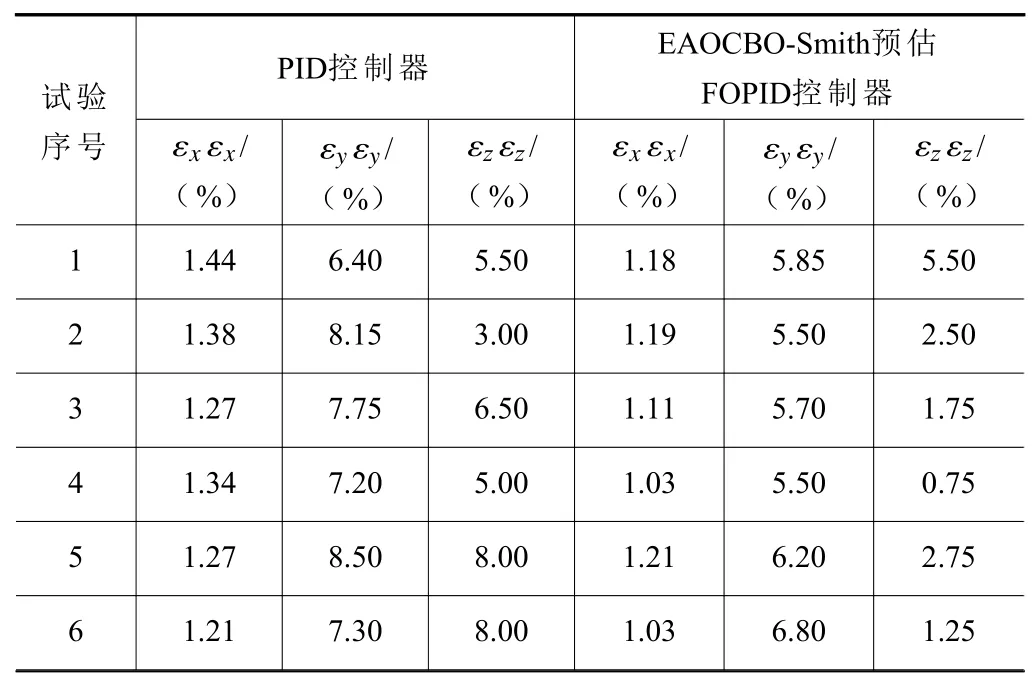
表3 不同控制器下成型件收缩率测量结果

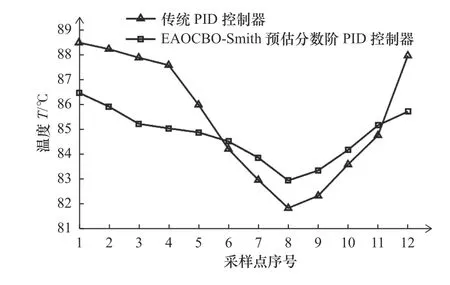
图9 各采样点的稳态温度对比图

图10 打印模型

图11 烧结过程图

图12 成型实物图

图13 模型测量

5 结语

针对SLS 过程中预热温度控制的非线性不确定性和时延滞后等问题，本文提出了一种改进预估分数阶PID 控制器用于温度控制。首先，在FOPID控制器中整合了Smith 预估器以消除纯时滞环节产生的震荡，提高被控系统的鲁棒性。然后，提出了名为EAOCBO 的敏感参数自整定方法，对预估FOPID 控制器的模型参数进行最优设计。为克服AO 探索和开发阶段的不平衡以及易于陷入局部最优的缺陷，引入了白冠鸡算法中的领导者更新机制，自适应切换系数以及折射反向学习策略。通过与5种算法在9 个IEEE CEC2017 测试函数上进行对比测试，证明了EAOCBO 具有更加优越的收敛精度和速度。为验证提出的EAOCBO-Smith 预估FOPID控制器的有效性，通过Matlab/Simulink 软件仿真分析了其在单位阶跃信号下的动态响应特性，本文所提出控制器的性能参数指标分别为上升时间0.215 s、峰值时间0.419 s、调节时间0.519 s、超调量2.4%、稳态误差0.001，相较于其他先进的FOPID 控制器有着更低的调节时间和稳态误差，证明了其出色的响应速度和控制精度。将其进一步应用于烧结样机预热温度控制并开展成型效果试验，当采用EAOCBO-Smith 预估FOPID 控制器时，粉床不同区域温度梯度变化更小、整体温度变化幅度较小，比PID 控制器更平稳，且成型件的 εx、 εy、 εz分别减小了0.193%、1.625%、3.584%。结果证明：本文提出的控制器可以更有效地控制温度，避免成型件出现收缩变形等缺陷，提高了成型精度，为选择性激光烧结预热温度的稳定精确控制提供了新的思路。