含大石块泥石流冲击作用下框架结构房屋动力响应研究

刘 欢, 樊晓一, 姜元俊, 刘浩南, 韩培锋, 田述军, 刘俊新

(1.西南石油大学 机电工程学院,成都 610500; 2.西南石油大学 土木工程与测绘学院,成都 610500;3.雅安市名山区住房和城乡建设局,四川 雅安 625100; 4.西南石油大学 工程安全评估与防护研究院,成都 610500;5.中国科学院 水利部成都山地灾害与环境研究所,成都 610299; 6.西南科技大学 土木工程与建筑学院,四川 绵阳 621010)

泥石流是一种常见的自然灾害,由地震、暴雨、冰雪融水等诱发,是介于挟沙水流和崩塌、滑坡等块体运动之间的固液两相流体,具有爆发突然、运动高速、体积大、破坏强等特点[1]。山区泥石流频繁发生,经常冲毁房屋建筑、道路桥梁等承灾体,掩埋村镇农田和阻塞河流,造成严重人员伤亡、巨大财产损失等灾害后果。

泥石流对建筑物的破坏为泥石流灾害中主要的损害方式,房屋建筑结构遭受泥石流冲刷作用是一种复杂冲击荷载作用下的非线性动力学问题[2],目前许多国内外学者开展了这方面的研究,其研究方法主要有试验方法、理论方法及数值方法。张宇等[3-4]在国内率先开展了铁球撞击砖混墙体的破坏性试验,采用钢板分散铁球冲击力模拟泥石流浆体冲击作用,结果验证了砖混结构墙体在泥石流冲击作用下的平面外受弯破坏形态,墙体振幅及位移随着冲量的增加呈指数趋势变化。曾超等[5]通过对汶川七盘沟泥石流实地调查和测量,分析不同建筑结构受泥石流冲击破坏模式,采用静力学极限平衡理论,提出柱体及墙体的破坏临界计算公式和建筑物五级破坏等级划分。雷雨等[6]基于砌体结构房屋受泥石流冲击的破坏模式,结合墙体弯曲应力破坏准则和冲击力计算方法,建立以泥石流流速和流深表示的砌体墙结构破坏模型和破坏曲线。Soleimankhani等[7]按照水动力学经验公式计算泥石流冲击力,采取数值方法反演意大利Scaletta Zanclea泥石流冲击砖混建筑破坏过程和动力特性,比较分析数值模拟结果与现场调查结果。Lu等[8]以铁球撞击框架柱模拟泥石流冲击过程,通过记录结构应变、位移和加速度来分析普通框架与泡沫铝加固框架在不同冲击能量下的破坏效应。

此外,基于各种数值模拟的方法正在被广泛运用。程选生等[9]采用有限元分析方法建立三维结构模型,从结构的整体变形、系统能量、关键点位移和速度等方面,研究泥石流作用下砌体结构的破坏机理和流固耦合动力特征,同时对比分析了三种防倒塌措施。李培振等[10-11]研究了泥石流冲击作用下砌体结构的破坏机理,讨论了黏性泥石流和稀性泥石流冲击作用下砌体结构的动态响应和破坏形式,同时进行了不同泥石流速度下结构响应的影响分析。Luo等[12]建立典型框架结构有限元模型,采用ALE(arbitrary Lagrangian-Eulerian)数值方法模拟泥石流动力作用,通过分析三种冲击速度下结构动力响应和破坏机理,提出了泥石流冲击作用下钢筋混凝土结构五级破坏等级体系。但在泥石流长距离运动与大变形计算时,上述基于有限元法(finite element method, FEM)的网格方法可能导致严重网格畸变问题,同时存在计算模型中荷载与结构耦合接触问题,比如没有考虑荷载-结构相互耦合接触或仅考虑泥石流浆体与结构的耦合力。

光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法是一种无网格方法[13],具有较强的自适应特性,可以很好地处理大变形问题,避免网格畸变造成的计算失败,可以很好地模拟流体的力学特性[14],但SPH具有施加边界条件困难、计算效率低等固有缺陷。而耦合SPH和FEM,能够同时发挥SPH计算大变形和FEM计算精度、计算效率高的优势。柳春等[15]利用SPH-FEM耦合模型研究了泥石流冲击混凝土拦挡坝的动力学问题,分析了泥石流的冲击被拦挡过程、冲击力时程、坝体关键点位移时程、坝体破坏等动力学行为、块石形状对冲击力影响。同时根据坝体破坏机理和结合工程实践,分析了减小迎坡比、增设防撞墩和增加缓冲层三种防撞优化对策。黄云[16]利用SPH-FEM耦合模型研究了桥墩在泥石流作用下的动力冲击问题。分析含大石块泥石流冲击桥墩的全过程、冲击力时程、关键点位移时程、桥墩破坏情况等动力学行为。这些都体现了SPH-FEM耦合方法在模拟泥石流冲击承灾体的适用性与精确性。

综上文献所述,目前这种含大石块泥石流与房屋框架结构之间的相互耦合动力学行为鲜有文献研究,现有研究成果无法满足实际工程的需要,因此有必要在既有研究成果的基础上,针对框架结构在泥石流冲击作用下的动力响应和力学行为展开进一步的研究,从而为山地建筑规划设计和防灾减灾提供一定的参考。

1 计算理论

1.1 SPH方法基础

SPH方法是模拟流体流动的一种拉格朗日型无网格粒子方法,是将计算域离散为一系列相互作用的粒子。通过这些粒子求解具有各种边界条件的积分方程或偏微分方程,得到稳定的数值解。SPH方程构造常按核函数插值和粒子近似两个关键步骤进行[17]。核函数插值实现场变量或场变量梯度的插值,而粒子近似实现对核函数估计积分表达式的粒子离散。

在SPH方法中,核心为插值,对于一个连续光滑函数f(r)在空间某一点r上的核估计,可通过函数f(r)在定义域中的积分获得

(1)

式中：<>为核近似算子;W(r-r′,h)为核函数,它的值取决于两点间的距离|r-r′|与核函数核半径κh;h为光滑长度,本文取光滑核函数的半径为2h。

光滑核函数不仅决定了函数近似式的形式、定义粒子支持域的尺寸,还决定了核近似核粒子近似的一致性和精度。目前常见的核函数有高斯型核函数、三次样条核函数、高次样条核函数等,本文采用目前常用的三次样条核函数来处理三维问题

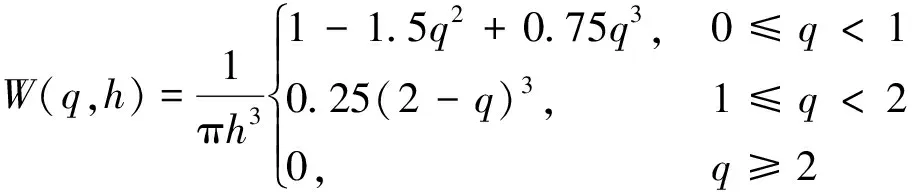
(2)

式中,q为粒子间相对距离,q=|r-r′|。

为了能够得到最终的离散控制方程,采用粒子近似方法对核函数插值离散,需通过对支持域内的一系列粒子的离散化求和来实现。若用粒子的体积Vj来近似积分中粒子j处的无穷小微元dr′,则粒子的质量mj可表示为

mj=ΔVjρj

(3)

式中：ρj为粒子j的密度(j=1,2,3,…,N),N为紧支域内的粒子总数。

对式(1)进行粒子离散化,有：

(4)

最终粒子i处的场函数值通过核函数对该粒子紧支域内所有粒子的函数值加权平均得到,即：

(5)

类似地,粒子i处场函数空间导数的粒子近似为

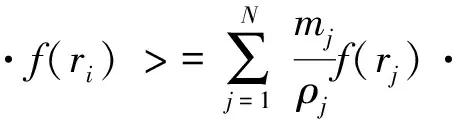
(6)

从式(5)和(6)可见,两式中的粒子近似将函数及其导数的连续积分转换成在任意排列粒子上的离散求和,这是SPH方法不需要网格进行计算的根本原因。同时引入了粒子的质量和密度,SPH粒子成为真实的具有材料特性的粒子,具有明确的拉格朗日特性。

在连续介质力学中,采用拉格朗日方式描述,常用质量守恒方程、动量守恒方程作为控制方程,将控制方程进行核近似和粒子近似可得SPH框架下的力学控制方程。考虑泥石流为弱可压缩流体,离散化方程[18]如下

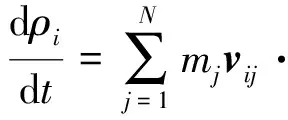
(7)

(8)

式中：vij为粒子i、j的相对速度矢量;σi,αβ和σj,αβ为各向同性压力和偏应力组成的总应力张量,下标α、β表示坐标方向;Fi为各种外力,如重力、摩擦力、接触力等。

1.2 SPH-FEM耦合方法基础

为了耦合SPH和FEM,关键点是计算SPH颗粒和FEM单元在接触界面处的相互作用力。SPH粒子与FEM单元之间的相互作用常采用点面接触形式,SPH粒子为接触从节点,FEM单元为接触主面,接触理论采用罚函数算法,通过罚函数算法将从节点的力施加到有限单元上。罚函数的基本原理相当于在SPH颗粒和FEM单元之间加上接触弹簧与阻尼,以此限制质点穿透主面。接触模型如图1所示。

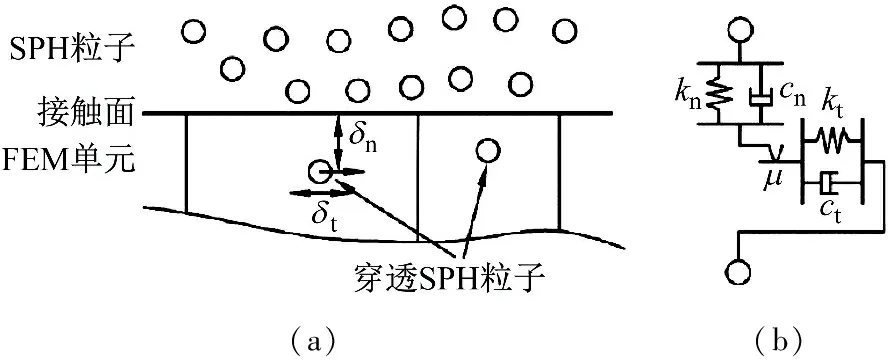
图1 SPH与FEM接触模型

在每个时间步长中,检查SPH粒子是否穿透主面。当穿透发生时,SPH粒子和主面之间将会产生接触力。法向接触力fn、切向接触力ft大小分别为[19]

(9)

(10)

式中：kn、kt分别为法向、切向弹簧刚度;δn、δt分别为法向、切向穿透位移;cn、ct分别为法向、切向阻尼系数;μ为摩擦因数。

kn和kt采用相同的计算方式,大小相等。

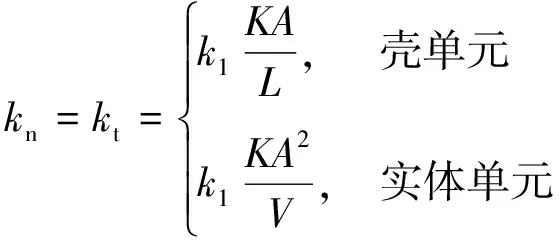
(11)

式中：k1为界面刚度的比例因子,通常默认为0.1;K为材料体积模量;A为接触段单元面积;L为壳单元最大对角线长度;V为接触段单元体积。

在求解耦合方程时,SPH采用条件稳定的跳蛙显式积分方法,FEM也采用条件稳定的中心差分法,两者耦合要求两者积分必须同步,这就要求两者在同一计算框架下每一步计算采用相同的计算步长,时间步长ΔtSPH-FEM取SPH时间步长ΔtSPH与FEM时间步长ΔtFEM的较小值。

2 建立计算模型

2.1 几何模型

利用三维建模软件建立几何模型如图2所示。模型由框架结构房屋、泥石流浆体、大石块、刚性地面及挡板组成。泥石流体积为20 m×20 m×2 m。大石块直径为1 m,考虑为刚性球体,位于泥石流的前端,垂直方向处于泥石流流深的1/2处[20],水平方向正对框架房屋的角柱。刚性地面尺寸为50 000 mm×21 000 mm×20 mm,两侧刚性挡板尺寸为50 000 mm×3 000 mm×20 mm。泥石流前端与框架结构房屋初始间距为3 m。

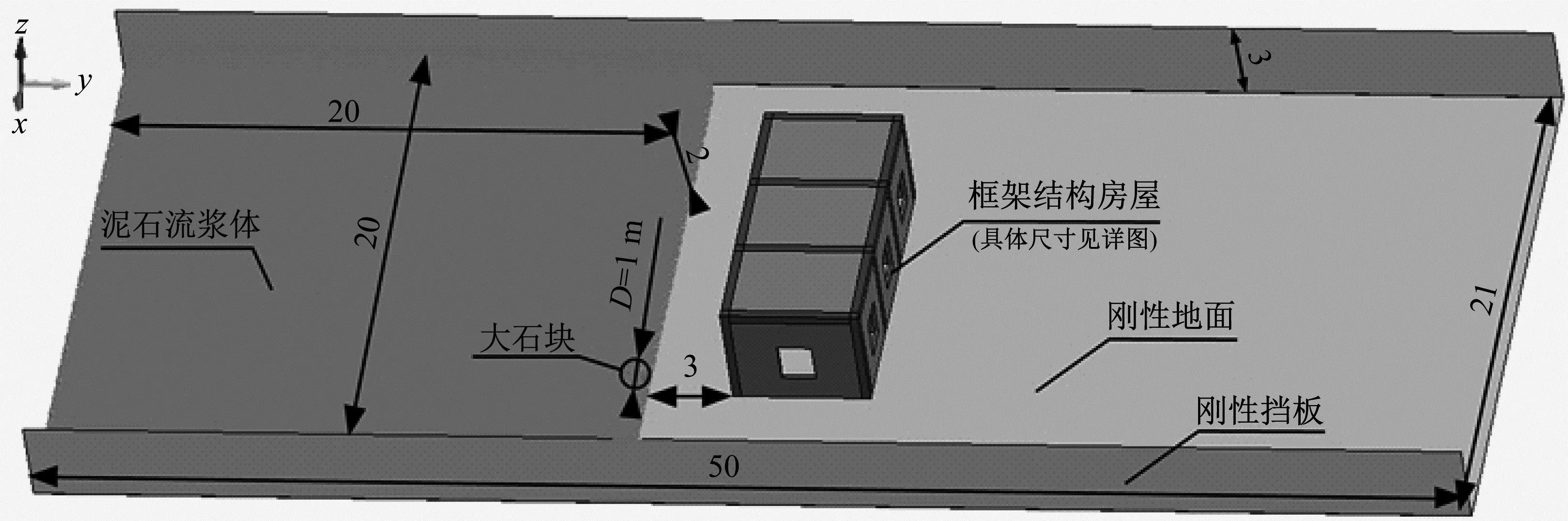
图2 几何模型(m)

房屋模型采用单层钢筋混凝土框架结构,结构总长10.2 m,宽4.5 m,高3.3 m。框架柱和框架梁的截面尺寸均为300 mm×300 mm,填充墙和楼板厚度均为150 mm。框架柱和梁的钢筋由纵向钢筋8Ф14和箍筋Ф8@200组成,楼板的横向和纵向钢筋为Ф14@200。窗户尺寸为1.2 m×1.4 m,距墙底0.9 m。假设门窗对泥石流的冲击没有抵抗力,因此没有对其进行建模。框架房屋的几何尺寸具体如图3所示。

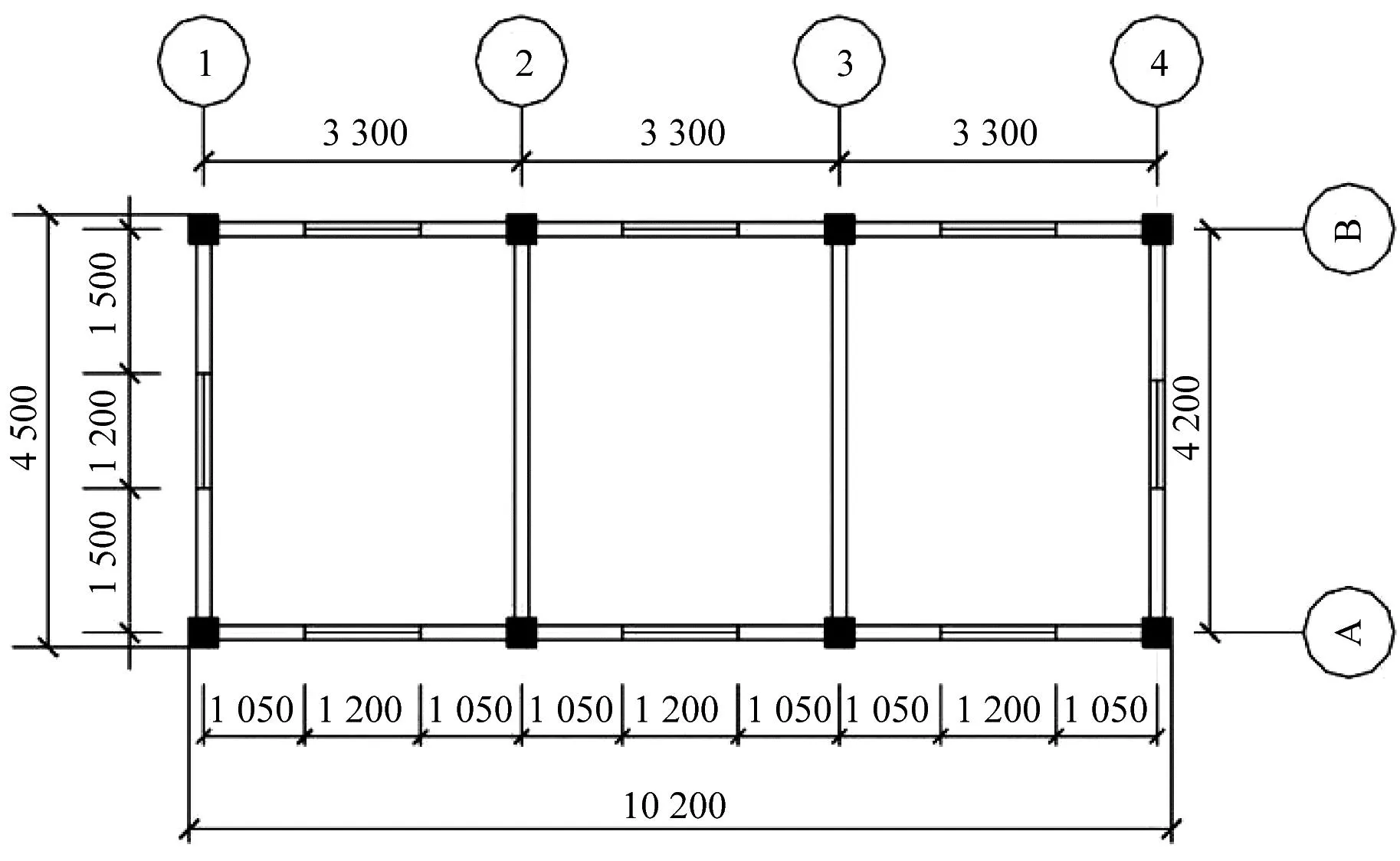
(a) 俯视图

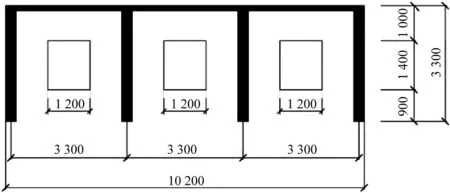
(b) 正视图

2.2 材料模型

混凝土材料：框架柱、梁、板构件由C25混凝土浇筑而成,混凝土材料采用连续盖帽模型[21](MAT_CSCM_CONCRETE),其失效破坏采用最大主应变失效准则[22]。当构件混凝土材料最大主应变超过0.05时,混凝土单元失效。其材料参数如表1所示。

砌体填充墙材料：使用HJC损伤材料模型(MAT_JOHNSON_HOLMQUIST_CONCRETE)对砌体填充墙进行模拟,其失效破坏采用最大主应变失效准则。当最大主应变超过0.003 3时,砌体填充墙单元失效。其材料参数如表2所示。

表1 混凝土材料参数

表2 砌体填充墙材料参数

钢筋材料：采用理想弹塑性材料模型(MAT_PLASTIC_KINEMATIC),材料密度为7 800 kg/m3,弹性模量为200 GPa,泊松比为0.3,屈服强度为335 MPa,失效主应变为0.1。

泥石流浆体材料：泥石流浆体是非牛顿流体,主要成分为碎石和砂土,其本构关系和动力特性非常复杂,采用弹塑性流体动力学材料模型(MAT_ELASTIC_PLASTIC_HYDRO)来近似模拟。状态方程定义为弱压缩性的线性多项式状态方程,暂不考虑黏性力的影响。采用SPH光滑粒子模拟泥石流浆体,SPH颗粒间距为0.2 m。其材料参数如表3所示。

表3 泥石流浆体材料参数

刚性材料：大石块、地面和挡板均采用刚性材料模型[23](MAT_RIGID),使用刚性材料模型不仅可降低分析耗时,提高计算效率,而且可防止分析过程中发生结构穿透。刚体材料密度为2 500 kg/m3,弹性模量为30 GPa,泊松比为0.3。

在数值模拟中,为了避免计算不收敛,经常使用侵蚀技术。如果任何单元达到规定的失效阈值,它将被假定对任何加载都没有阻力,然后从计算中删除。在本文中,混凝土(梁、板、柱)、砌体(填充墙)、钢筋(纵向钢筋、箍筋)的破坏准则是基于模型材料的最大主应变[24]。当达到材料最大主应变时,计算程序则自动删除相应单元。本文利用侵蚀算法可以观察到房屋的渐进倒塌过程。

2.3 计算单元及网格划分

柱、梁、板、填充墙、大石块采用SOLID实体单元模拟,共有41 428个实体单元。钢筋采用BEAM梁单元模拟,共有10 189个梁单元。地面及挡板采用SHELL壳单元模拟,共有21 696个壳单元。泥石流采用SPH粒子模拟,共有102 010个粒子。

利用专业网格划分软件对模型进行网格划分,为节省计算时间和保证计算精度,各构件的最小网格单元大小尽量保持相同或接近。截取其中框架房屋和大石块网格划分模型如图4所示。

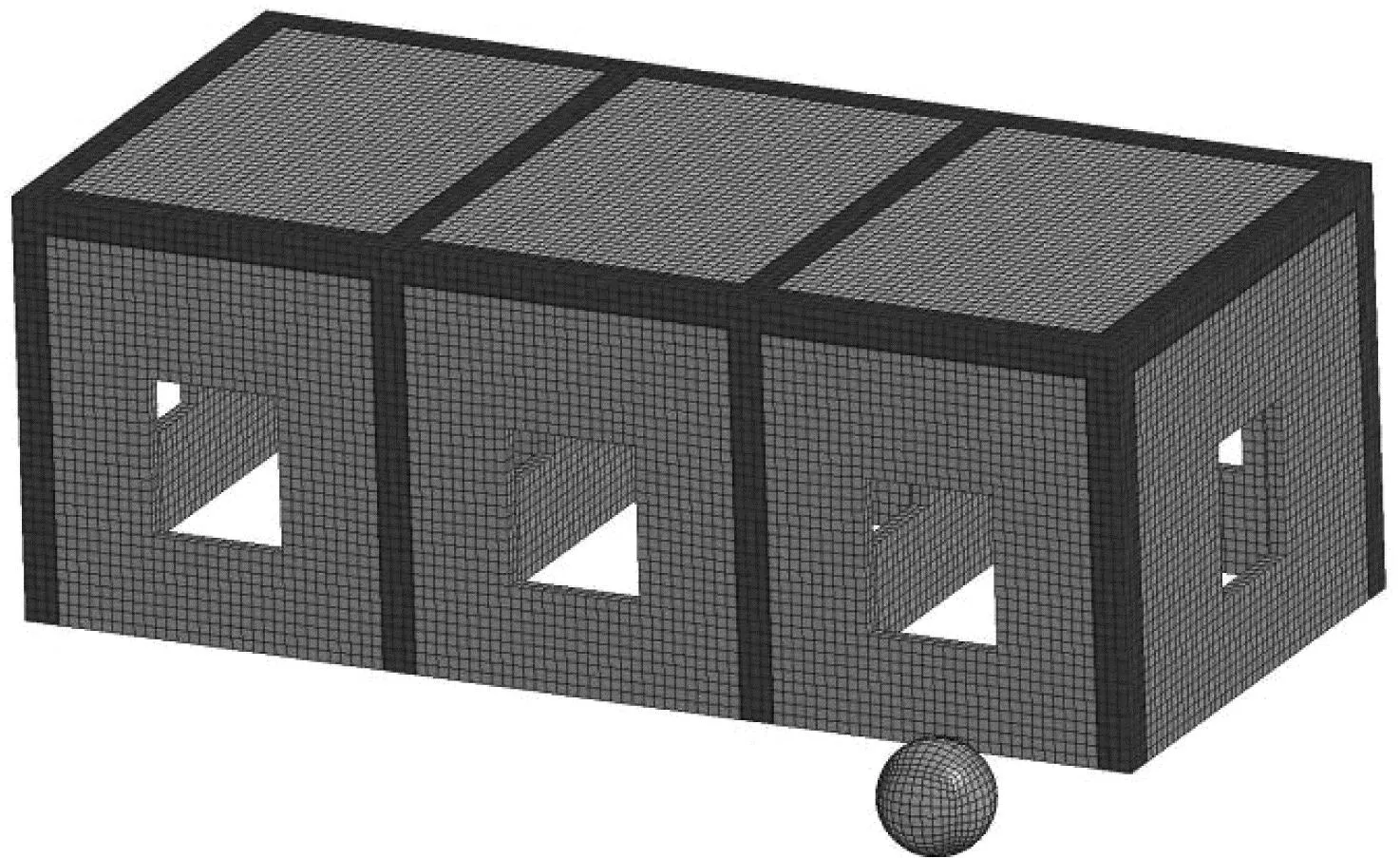
图4 网格划分

2.4 边界条件及荷载施加

泥石流浆体与框架柱、梁、板、填充墙、大石块、地面、挡板之间采用自动点-面接触[25](Contact_Automatic_Nodes_to_Surface),静摩擦因数为0.2。考虑到大石块表面的粗糙度,大石块与框架柱、梁、板、填充墙、地面之间采用自动面-面接触(Contact_Automatic_Surface_to_Surface),静摩擦因数为0.4。大石块与钢筋之间采用自动梁面接触(Contact_Automatic_Beams_to_Surface),静摩擦因数为0.4。

刚性地面和房屋底部采用全固定约束边界。房屋框架柱、梁、板之间采用共节点连接形式。框架柱与填充墙之间的连接采取沿其高度方向间隔0.5 m共节点固结相邻网格单元,以模拟实际中拉结钢筋的连接作用。钢筋单元嵌固在混凝土单元内,用CONSTRAINED_LAGRANGE_IN_SOLID(LS-DYNA程序的关键学)来定义钢筋与混凝土之间的约束,能实现动量守恒和力的平衡,钢筋与混凝土受力变形方式相同。

考虑结构的自身质量,重力加速度为9.8 m/s2。根据GB 50009—2012《建筑结构荷载规范》,在楼面施加2.0 kN/m2的均匀分布荷载,不考虑风荷载、地震荷载等其他荷载。假设泥石流与大石块保持相同的初始速度,泥石流流动方向垂直于框架结构房屋纵向,正面冲击房屋正立面。模拟计算总时间设定为2 s,可以模拟泥石流冲击框架房屋的全过程。

2.5 变量参数

为分析是否含大石块对泥石流冲击特性的影响,本文设置含大石块泥石流和纯浆体泥石流两种工况。同时为考虑不同冲击速度的影响,根据泥石流对建筑房屋冲击破坏程度情况,分别设置了低(流速为6 m/s)、中(流速为8 m/s)、高(流速为10 m/s)三等冲击强度工况。

3 结果分析

3.1 冲击过程及破坏形态

以中等冲击强度的含大石块泥石流为例,演示其冲击框架房屋的过程如图5所示。当t=0时,泥石流浆体与大石块以8 m/s的初始速度流动。当t=0.35 s时,泥石流龙头到达框架房屋。大石块冲击框架角柱,产生较大的局部冲击力,角柱部分钢筋混凝土因最大主应变超过失效应变限值而破坏,并从计算中删除;泥石流浆体冲击框架填充墙,填充墙体由于平面外抗弯能力较低而失效,泥石流涌入房屋框架内部形成过流通道。当t=1.00 s时,泥石流到达框架房屋后排填充墙,后排填充墙失效,大石块冲坏后方角柱。过程中,由于房屋结构的拦挡作用,可以发现部分泥石流浆体顺着墙体与柱攀爬升高,同时部分泥石流浆体绕过房屋向两侧扩散并向下顺流。当t=2.00 s时,框架边跨由于泥石流和石块冲击导致该跨整体失稳破坏。最终由于摩擦作用,泥石流停止流动堆积于房屋周围。全程模拟了泥石流启动运动、冲击爬高、绕流扩散、淤积稳定等过程。

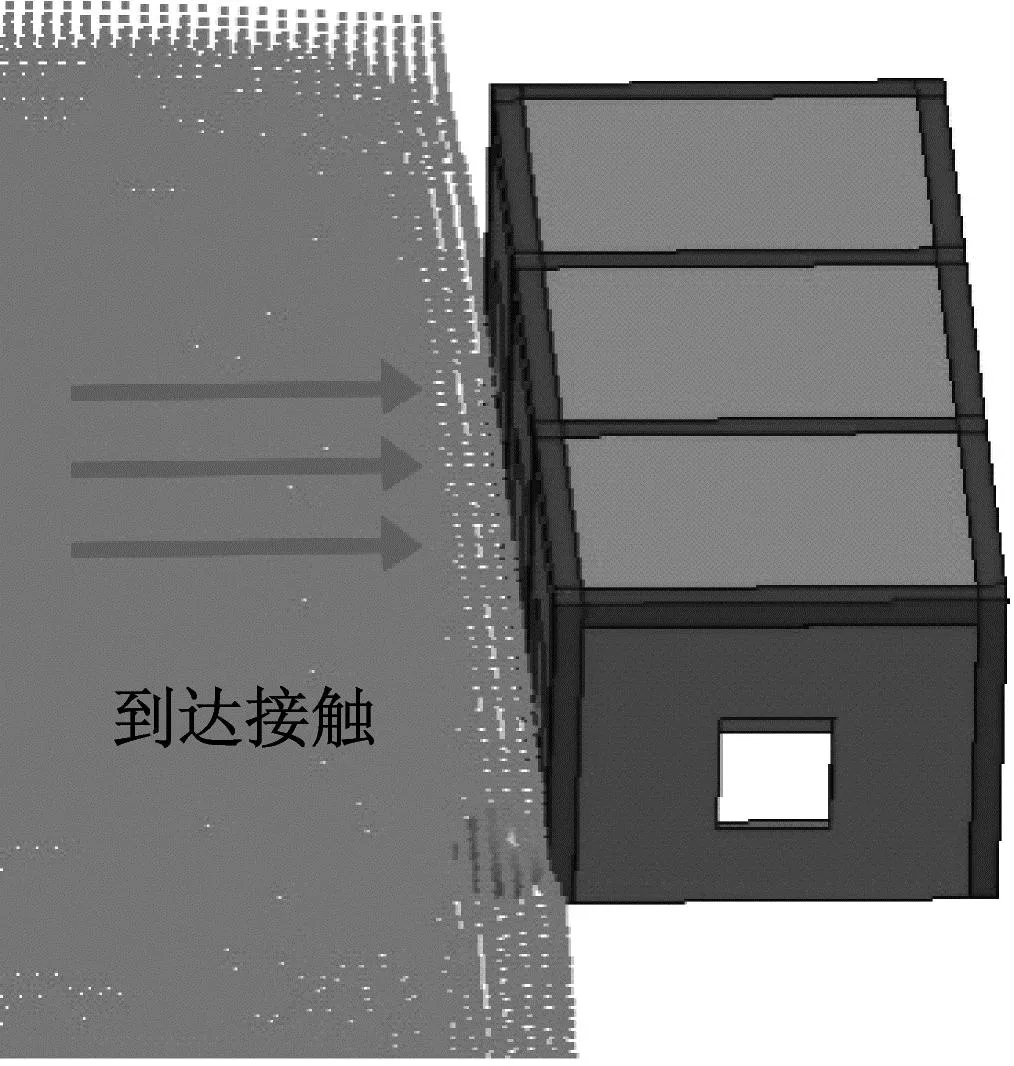
(a) t=0.35 s

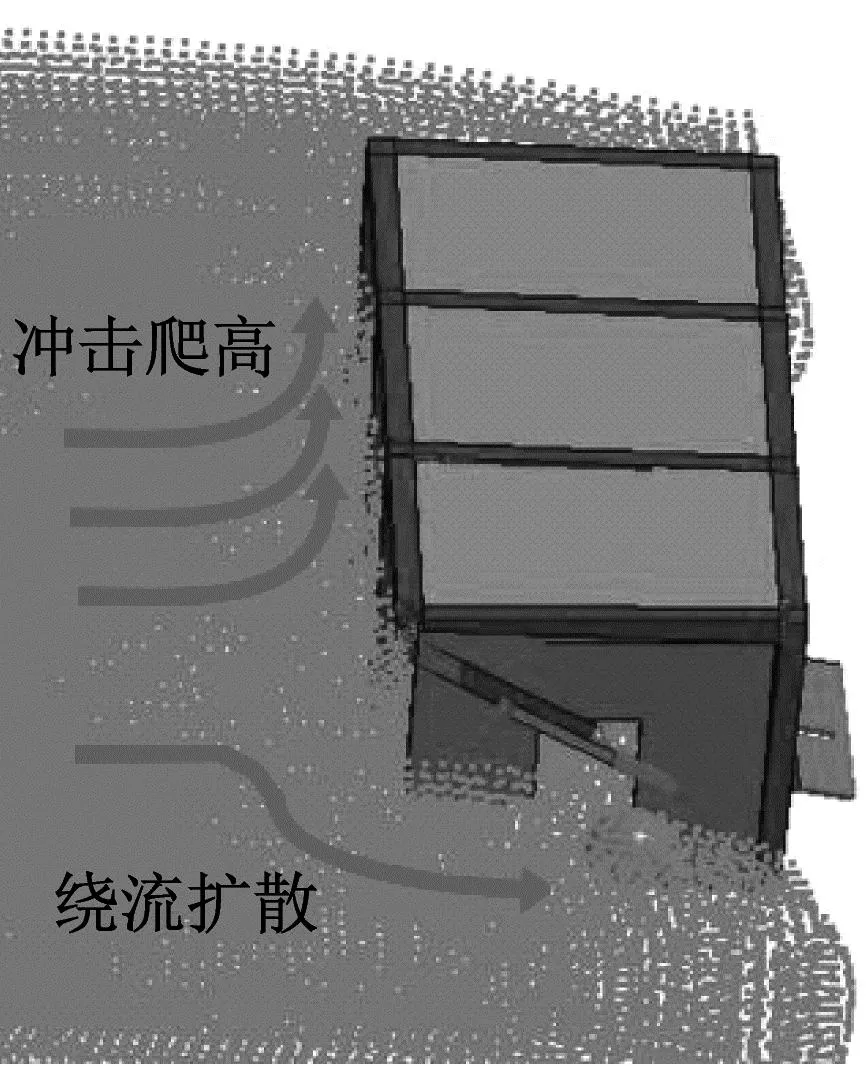
(b) t=1.00 s

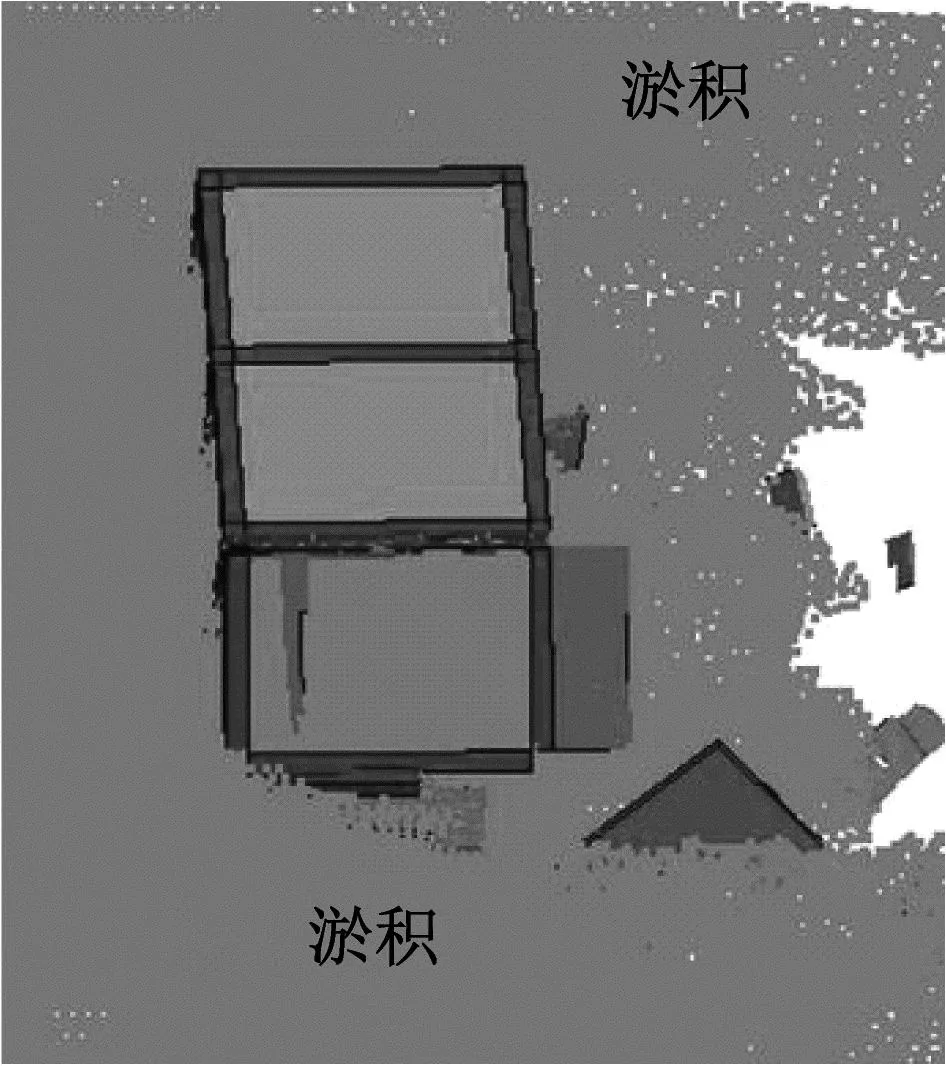
(c) t=2.00 s

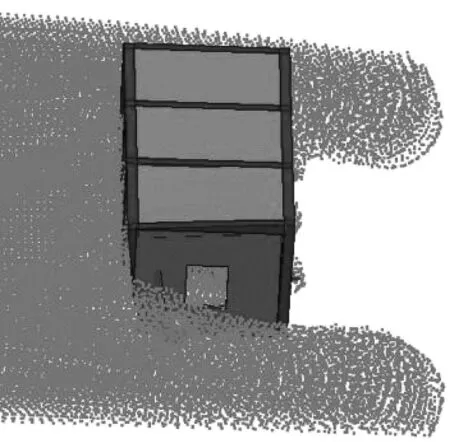
图6显示了低等冲击强度下房屋的破坏形态。在这种情况下,可以观察到房屋前排墙体受到破坏,其破坏的主要原因是面外抗弯能力较低。泥石流流入房屋内部,到达房屋后排墙体。此时泥石流流速约为3 m/s,由于泥石流动能较低,没有冲坏后排墙体,后排墙体和主要结构构件没有损坏。此外,在大石块的局部冲击作用下,前排角柱及其后方侧墙发生局部破坏。

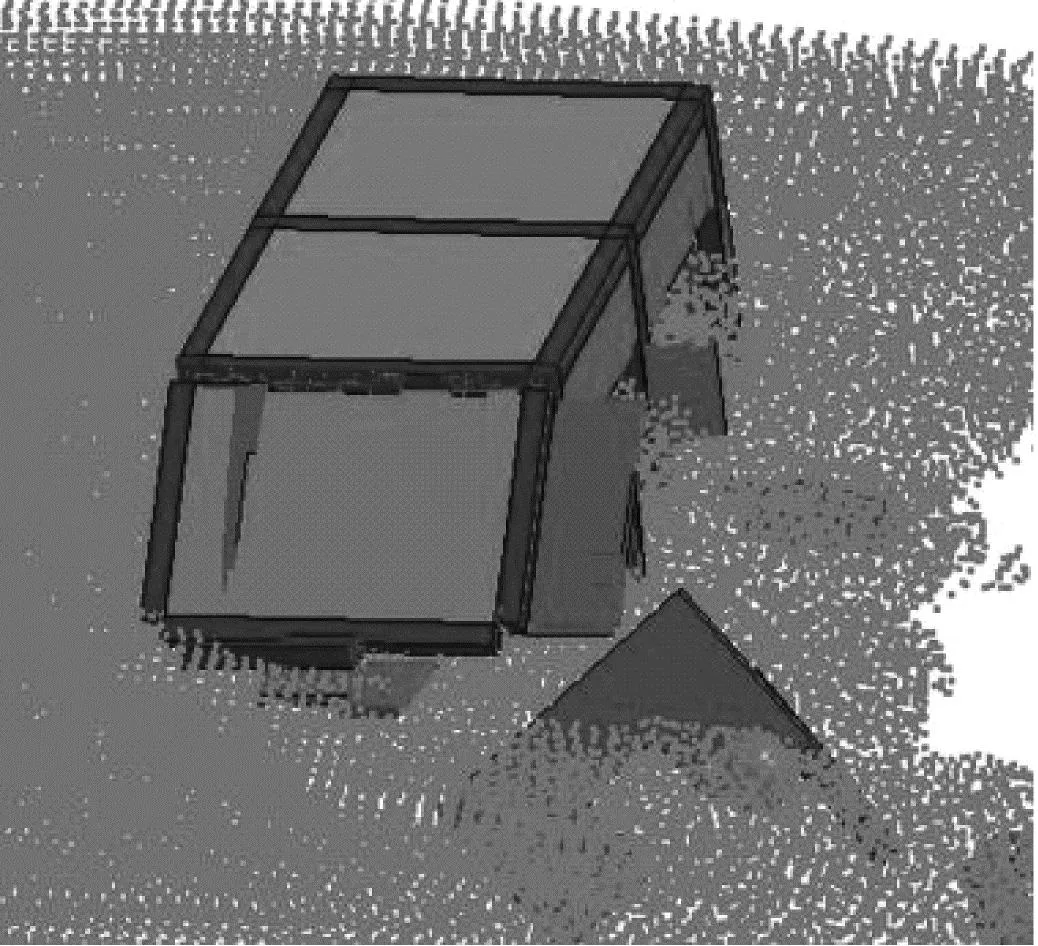
四川都江堰龙池泥石流灾毁现场可以观察到与此类似的建筑破坏形态,如图7(a)所示。该建筑应对泥石流冲击前端有其他建筑遮挡,且位于泥石流的较远端,泥石流到达时前缘动能较小,只造成房屋墙体破坏,房屋结构整体保持稳定。

(a) t=2.00 s

(b) 含大石块

(c) 无大石块

(a) 都江堰龙池泥石流(低等冲击强度)

(b) 都江堰龙池泥石流(中等冲击强度)

(c) 汶川七盘沟泥石流(高等冲击强度)

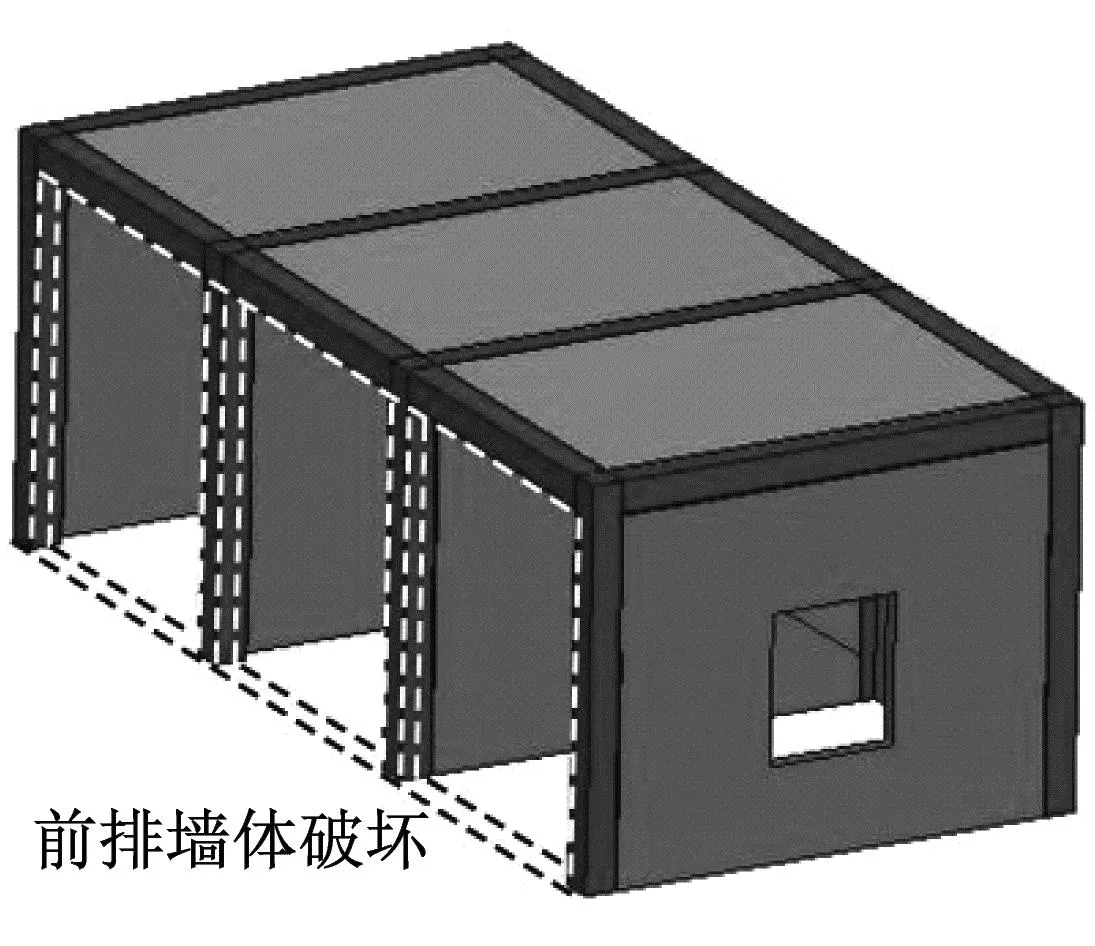
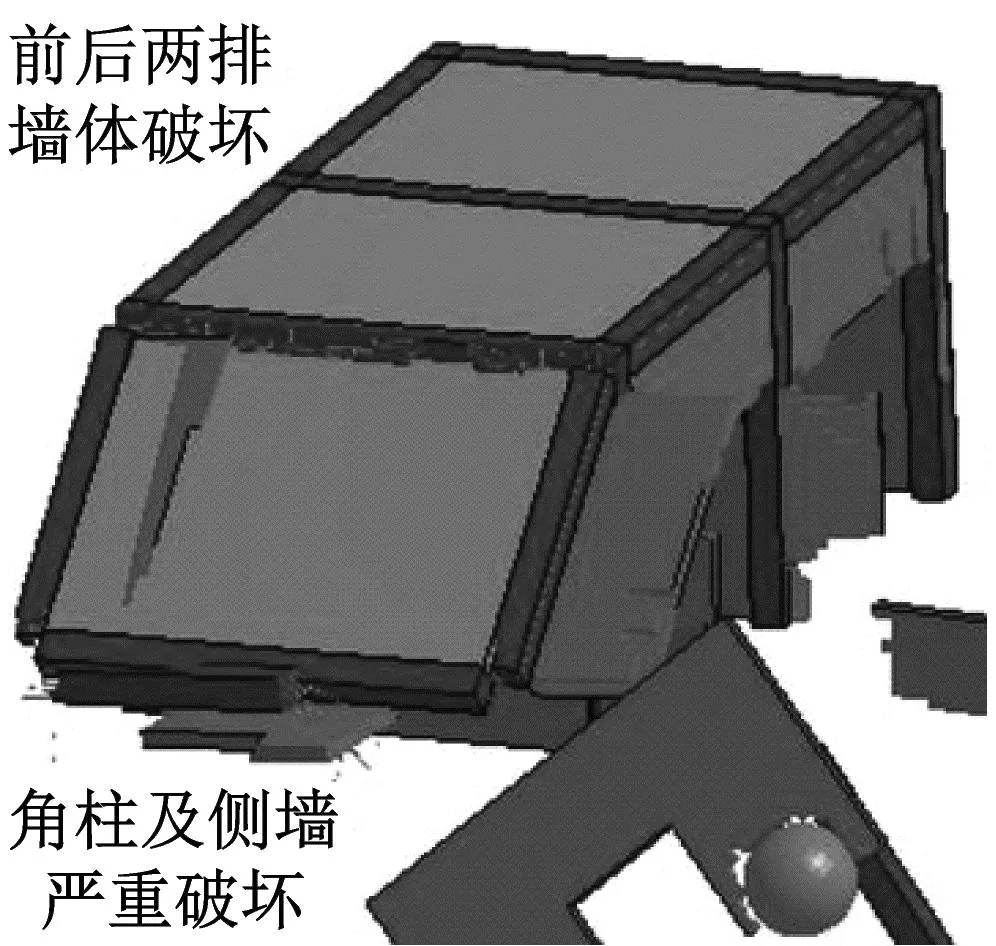
图8显示了中等冲击强度下房屋的破坏形态。在前排墙体失效后,泥石流流入房屋内部,并冲坏了后排墙体。在这种强度冲击下,泥石流的动能不足以导致框架主要受力构件损坏,房屋没有整体倒塌。此外,在大石块的局部冲击作用下,角柱及其后方侧墙发生严重破坏,该跨框架整体失稳。

在图7(b)四川都江堰龙池泥石流灾毁现场可以观察到与此类似的建筑破坏形态。泥石流冲坏房屋墙体,大石块对柱体造成严重破坏。说明大石块的集中冲击作用是造成结构受力构件局部破坏的主要原因,在泥石流模型中不可忽略。

(a) t=2.00 s

(b) 含大石块

(c) 无大石块

图9显示了高等冲击强度下房屋的失稳形态。与中等冲击情况不同的是,由于泥石流高强度冲击,框架柱和墙体遭受严重破坏,整个框架失稳倒塌,房屋主体被泥石流冲走,致其完全破坏。框架柱损坏主要是由于泥石流作用达到其极限弯矩或极限剪力,体现了塑性铰链失效或剪切破坏机制。

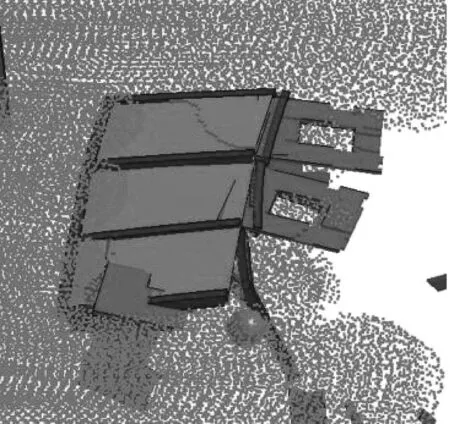
(a) t=2.00 s

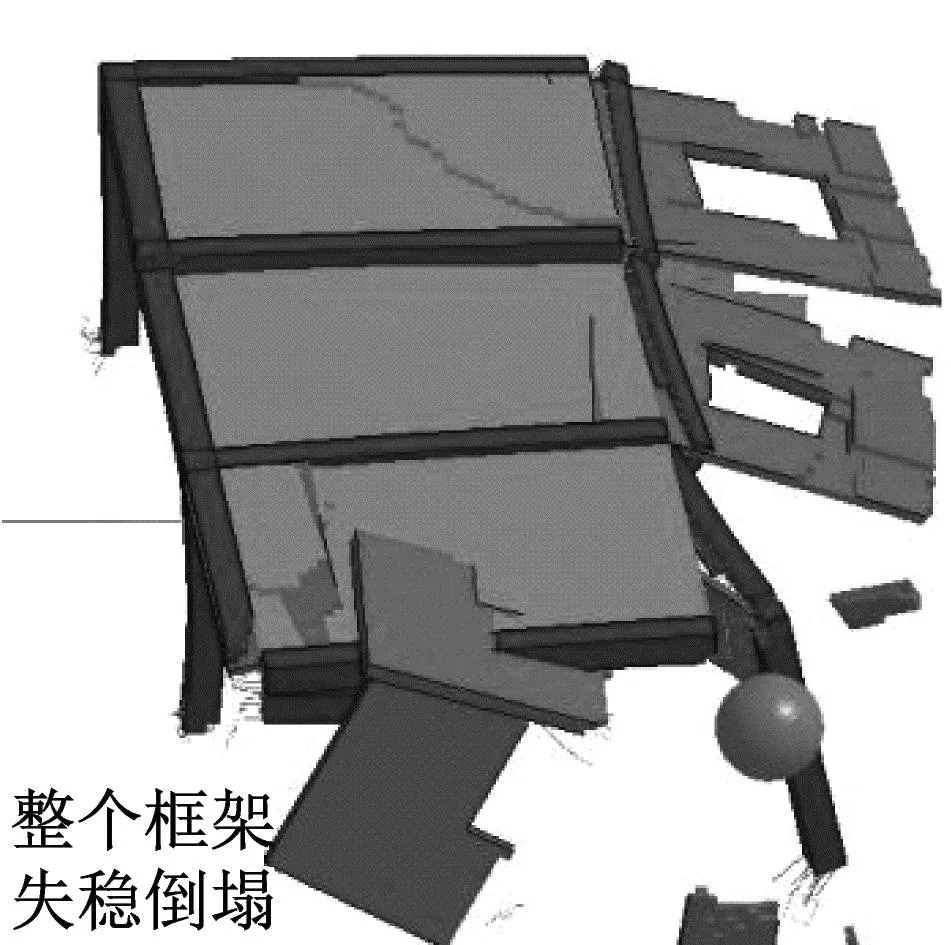
(b) 含大石块

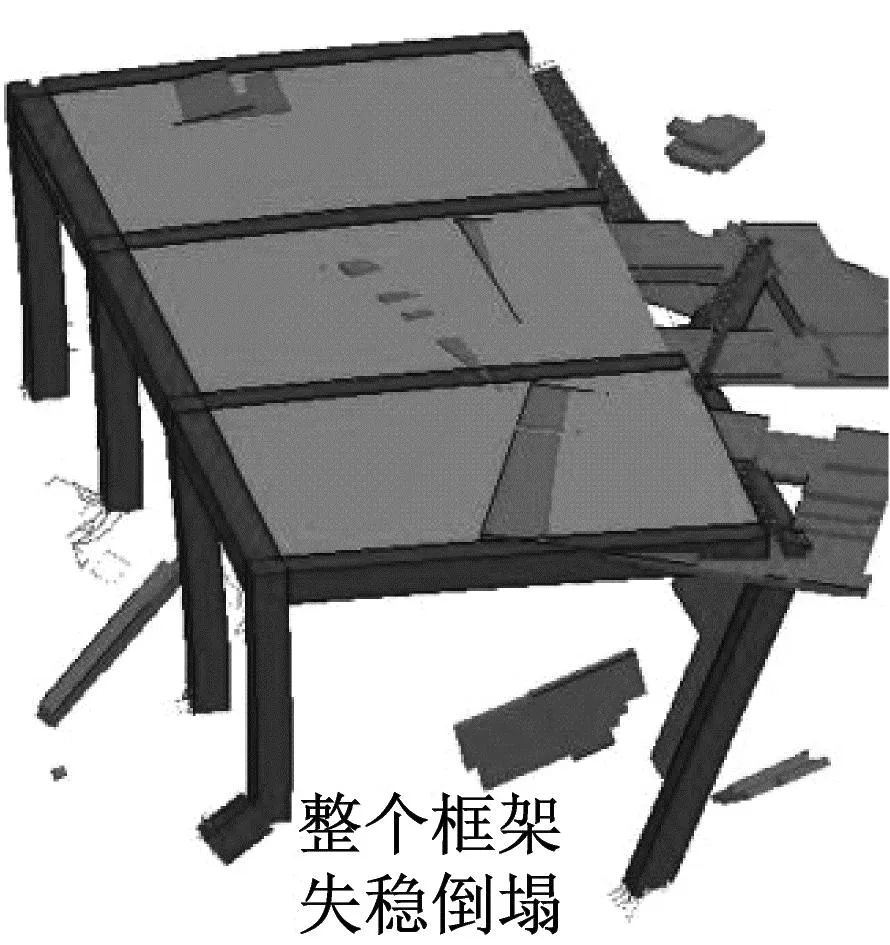
(c) 无大石块

在图7(c)四川汶川七盘沟泥石流中[26]观察到这种高等冲击强度下的建筑破坏形态。框架结构柱与梁被泥石流直接剪断或产生塑性铰,此后框架结构整体向泥石流运动方向倾倒。

3.2 冲击力

泥石流冲击力包括浆体冲击力和大石块冲击力[27]。浆体冲击力整体作用于结构上,其合力往往很大,且作用面积也很大,具有一定的破坏性。大石块冲击结构时作用面积小,瞬时的巨大局部冲击力容易造成结构的局部破坏,由于连锁效应引起结构失效。泥石流浆体和大石块在泥石流中并不是独立的,而是相互耦合作用的。

图10为框架结构承受泥石流浆体冲击力时程曲线。从整体上看,曲线有两个峰值,对应于泥石流冲击框架结构前后两榀。泥石流垂直冲击于房屋正立面,直接承受泥石流冲击的房屋构件为框架柱和填充墙,对于泥石流浆体冲击力而言,是否含有大石块对时程曲线趋势变化没有影响。从图10可以看出,以泥石流流速8 m/s曲线为例,泥石流浆体首先作用在框架前排柱和填充墙上,框架房屋整体所受的冲击力随着前排填充墙的破坏而瞬间下降减小,此时框架柱主要承受泥石流浆体冲击力。之后由于结构的阻力和泥石流的摩擦耗能,使后排的框架柱、填充墙冲击力峰值降低,平均降幅约34.2%。在低(流速6 m/s)、中(流速8 m/s)等冲击强度作用下,框架柱没有破坏,框架结构承受泥石流浆体的冲力随着冲击速度增大而增大;在高等冲击强度作用下,框架柱钢筋和混凝土材料达到失效应变而破坏,造成框架柱部分单元从计算中删除,导致框架结构承受泥石流浆体的冲击力数据失效。

在图11大石块冲击力时程曲线中,低等冲击强度下大石块初始最大冲击力为103 kN,大石块初始速度较小,且泥石流浆体与大石块存在耦合作用,促使大石块加速冲击框架角柱,最大冲击力达到146 kN;中、高等冲击强度下大石块最大冲击力为113 kN和116 kN,与房屋角柱接触到分离历时约0.1 s,表现为集中脉冲荷载形式。

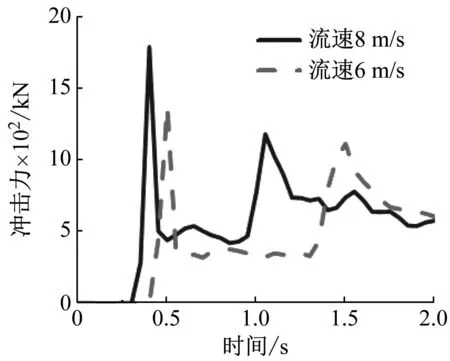
(a) 含大石块

(b) 无大石块

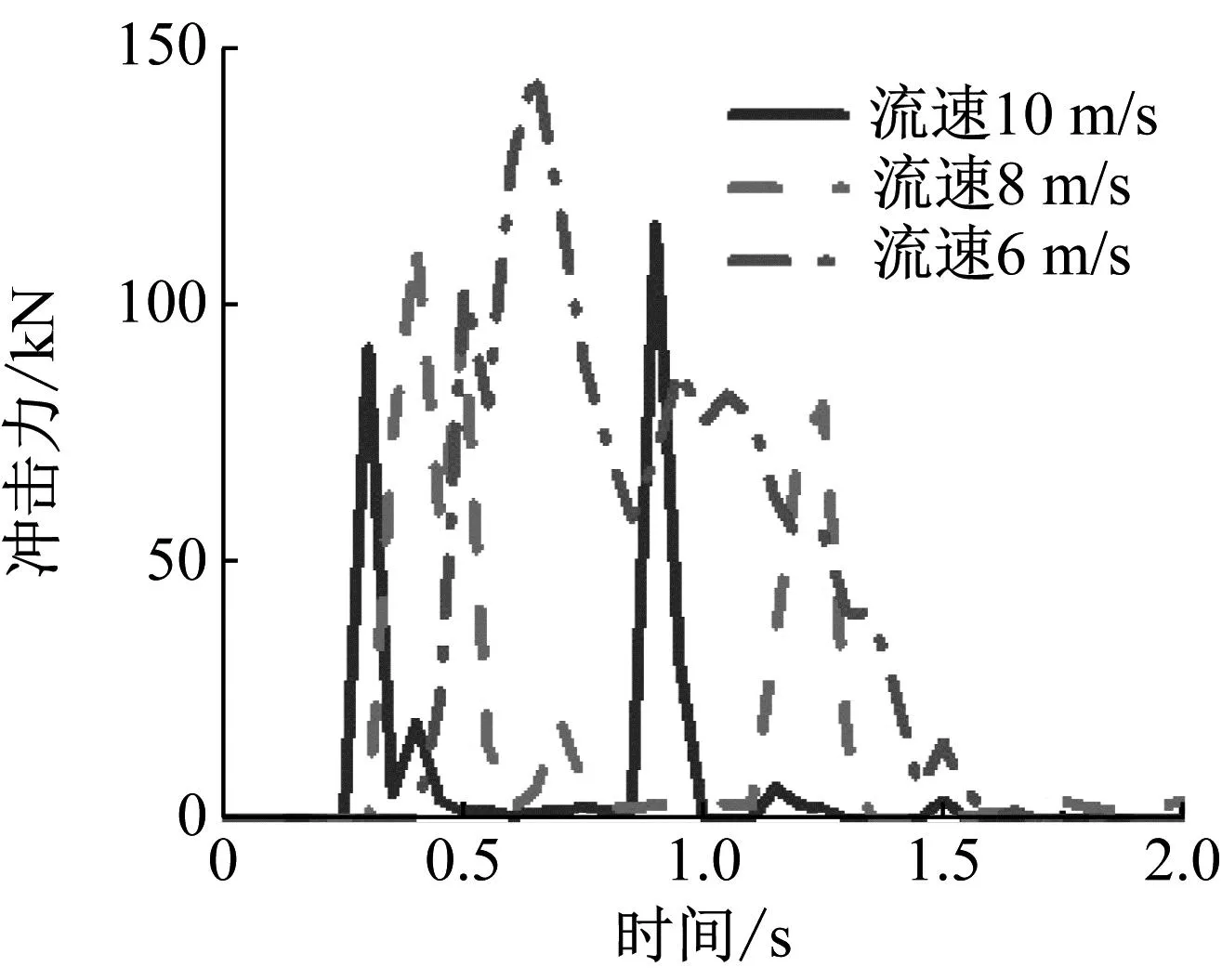
图11 大石块冲击力时程曲线

3.3 关键点位移

在后处理中提取框架柱Y方向位移云图,如图12所示。由图12可知,框架柱在泥石流作用下的最大位移集中在距离地面1.5 m附近的位置。为了获取前排未失效框架柱位移情况,通过绘制柱上关键单元点位移时程曲线来研究其位移变化过程。分别取框架柱高1.5 m处的四个关键单元点A248、B1448、C2396、D3269,如图13所示。由于有石块冲击框架柱,框架A柱破坏,故位移时程曲线里不考虑A点位移。同样当v=10 m/s时,框架柱受到破坏,也不考虑柱上关键点位移。编号B-8(1448)表示：在8 m/s冲击速度下,关键点B1448的位移,下文关键点速度编号表示与此相同。

柱上关键点位移随着冲击速度的增大而增大,如图14所示。在低等冲击强度下,框架柱关键点位移变形曲线几乎重叠,最终位移大小接近0.02 m。在中等冲击强度下,位于两侧的框架柱关键点位移稍小,最终的位移大小在0.06 m左右;中间的两根框架柱关键点位移较大,最终位移大小在0.07～0.08 m。由此可得,在泥石流冲击作用下,结构所受到的冲击力是对称分布的,中间的框架柱承受较大的冲击力。

图12 框架柱Y向位移云图

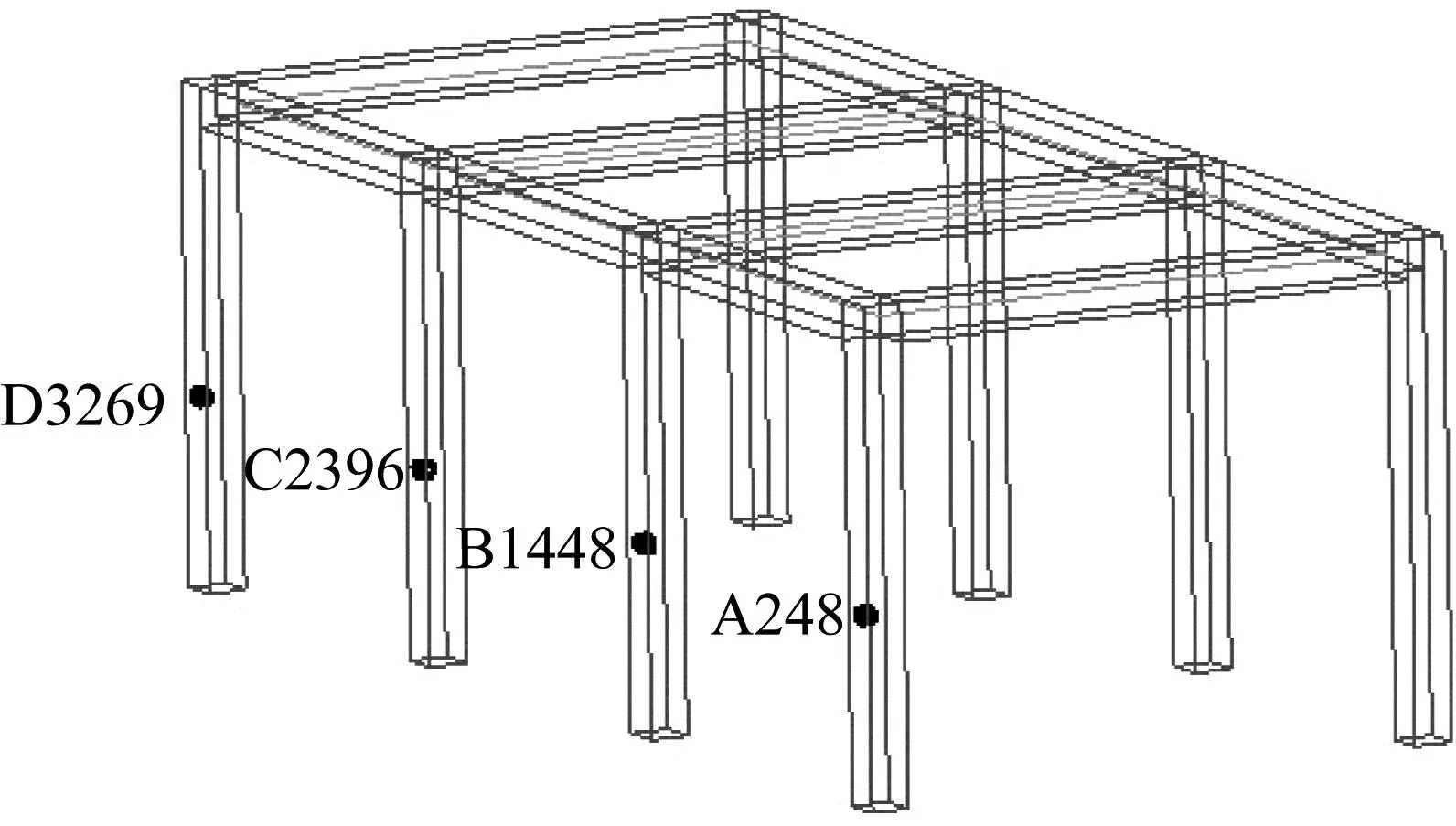
图13 框架柱关键点位置

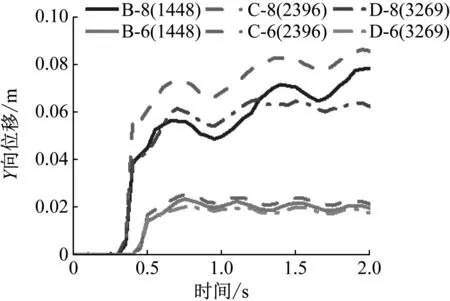
(a) 含大石块

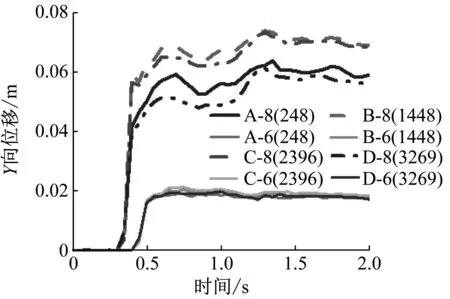
(b) 无大石块

3.4 关键点速度

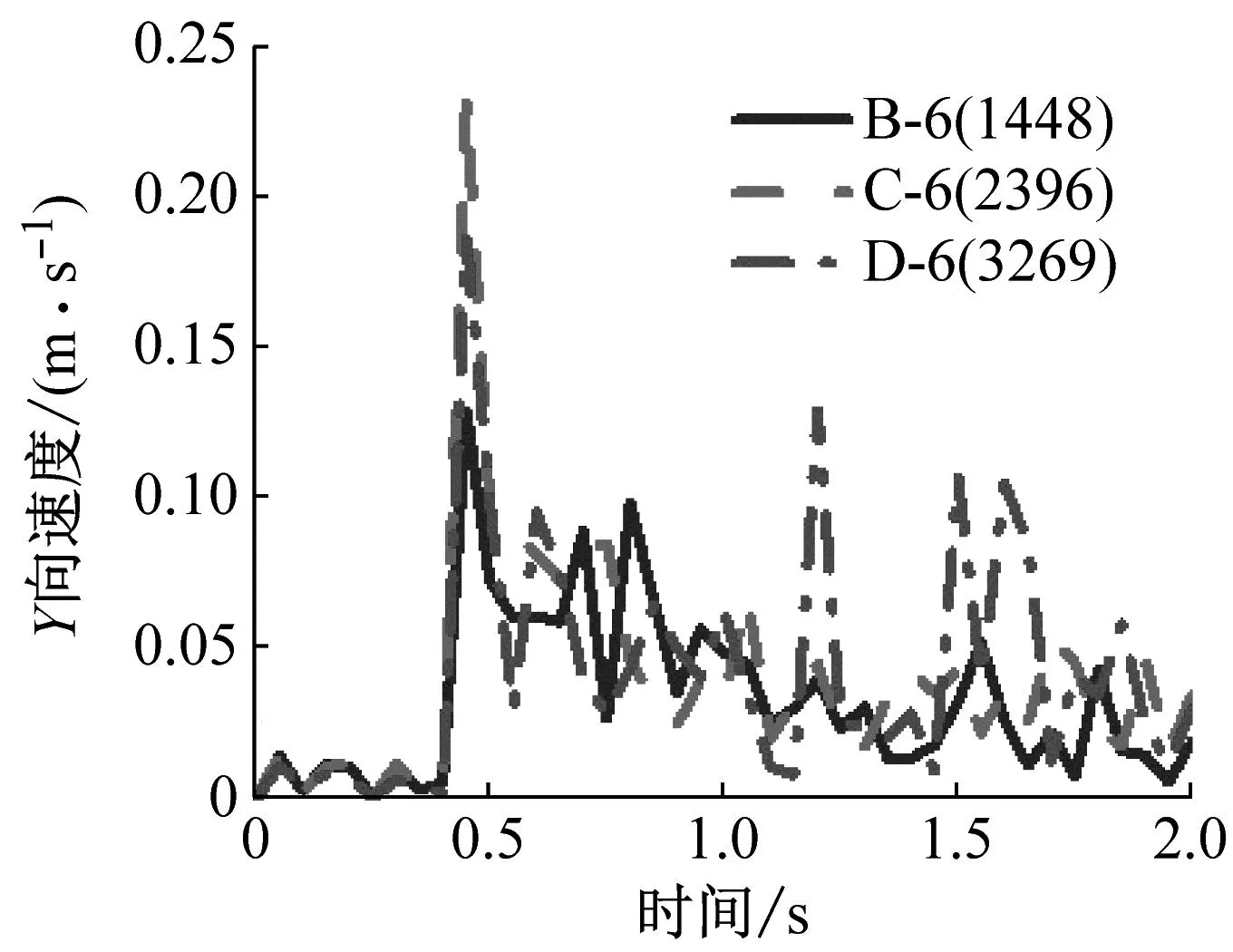
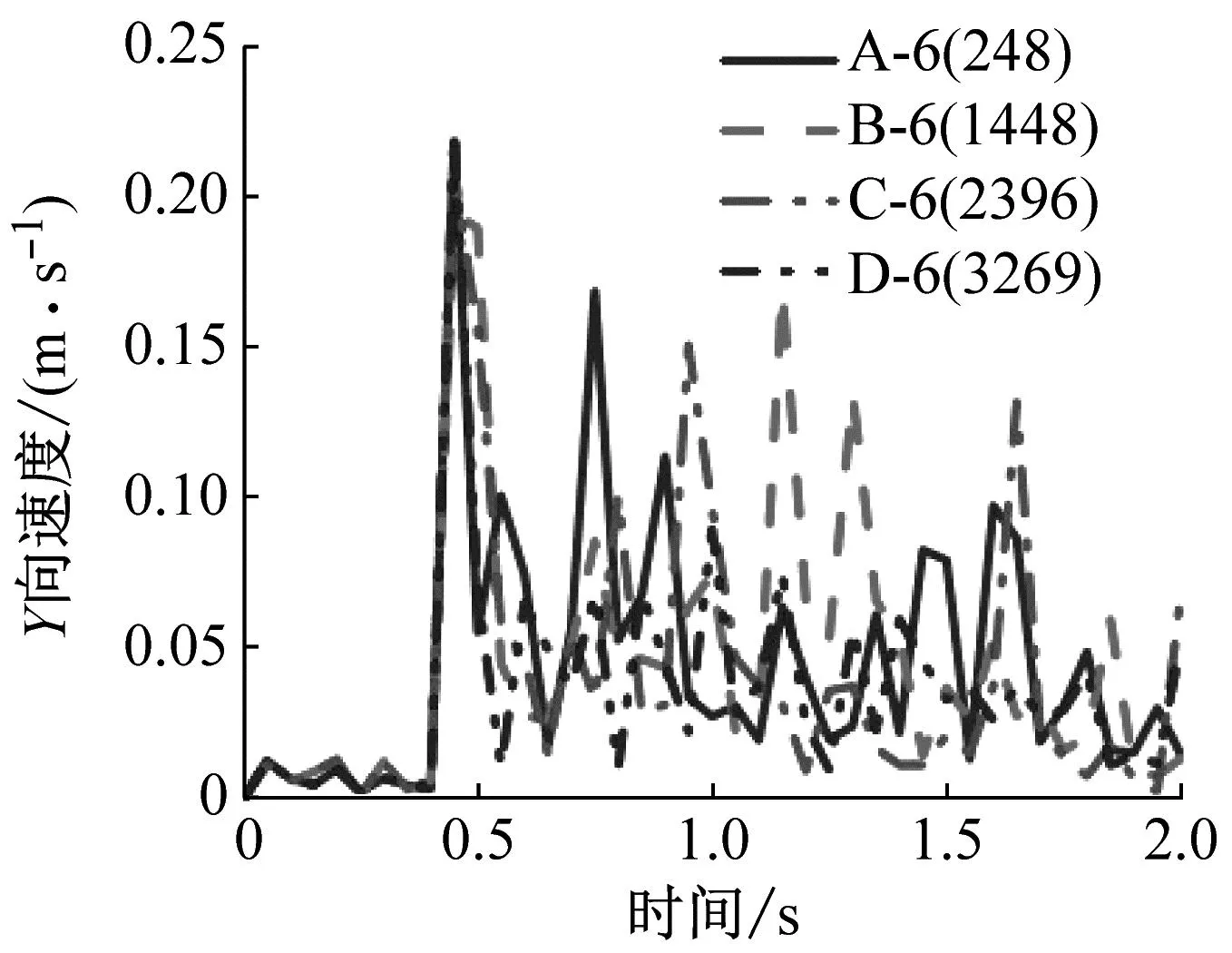
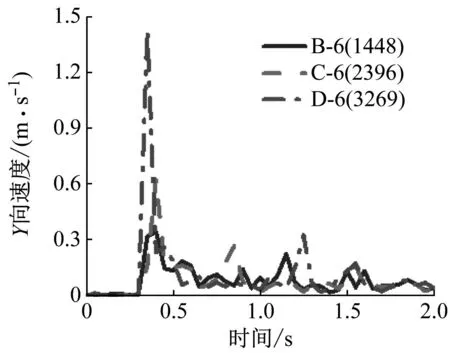
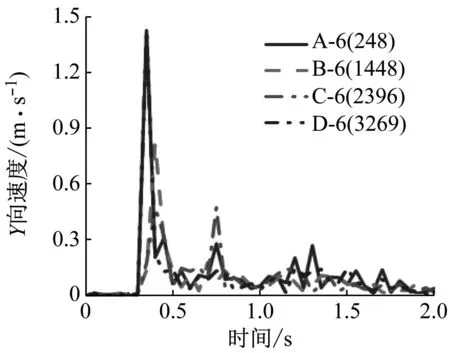
在动力分析过程中,节点速度是一个重要参数,节点速度的过程曲线可以用来衡量结构局部或者整体破坏状态的发展。本文把这四个关键点速度随时间变化的过程用曲线绘制出来,关键点的速度曲线如图15、图16所示。

(a) 含大石块

(b) 无大石块

(a) 含大石块

(b) 无大石块

由图15和图16可知,框架柱发生的变形在很短时间内完成,从产生变形开始到结束约0.15 s,关键点速度在泥石流龙头冲击作用下很快增长到最大值。而后,由于框架结构的阻力,速度急速减小,并保持在很小的范围内波动。由此可得：泥石流的冲击破坏能力主要来自于龙头的冲击力。因此对于结构而言,如果能够承受泥石流龙头的冲击力,就能够避免整体结构倒塌的危险。同时,柱上关键点速度峰值随着冲击速度的增大而增大。

3.5 系统能量

不同冲击速度下泥石流能量的变化如图17所示。该模型是否含大石块对于系统能量的影响很小,可以忽略不计。当t=0时,初始速度为6 m/s、8 m/s、10 m/s的泥石流动能分别为22 823 kJ、40 570 kJ、63 396 kJ。系统能量主要是通过泥石流动能与结构内能、摩擦耗能相互转换体现出来。开始作用之前系统总能量以动能的形式表现,之后逐渐转换为结构内能和摩擦耗能,且主要为泥石流与地面、泥石流之间的摩擦耗能。其中房屋消耗能量较少(17.8%),主要靠摩擦力耗散能量(82.2%)。同样表明,有效的防护措施可以最大程度消耗泥石流的能量,保证结构的安全性。

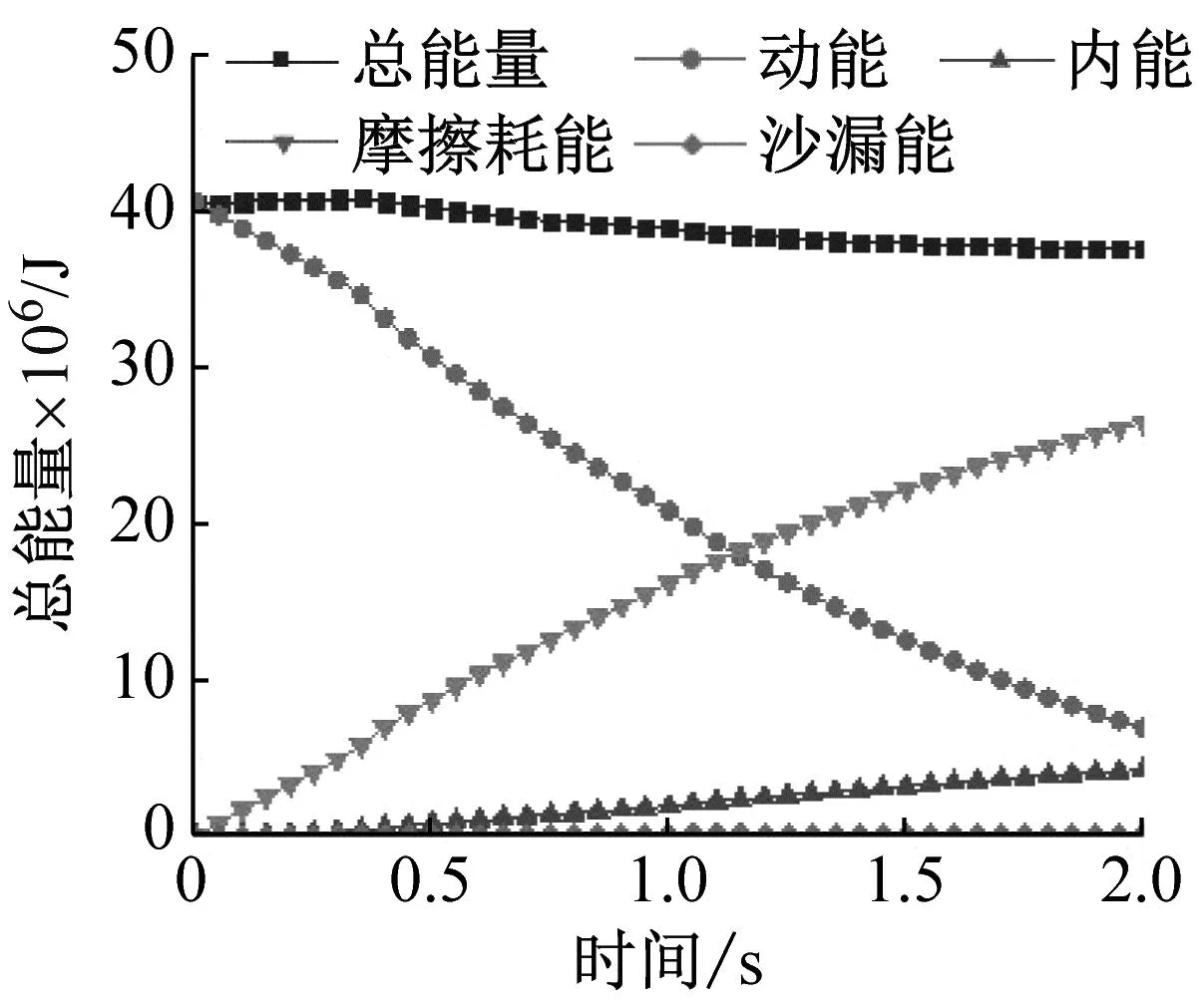
(b) v=8 m/s

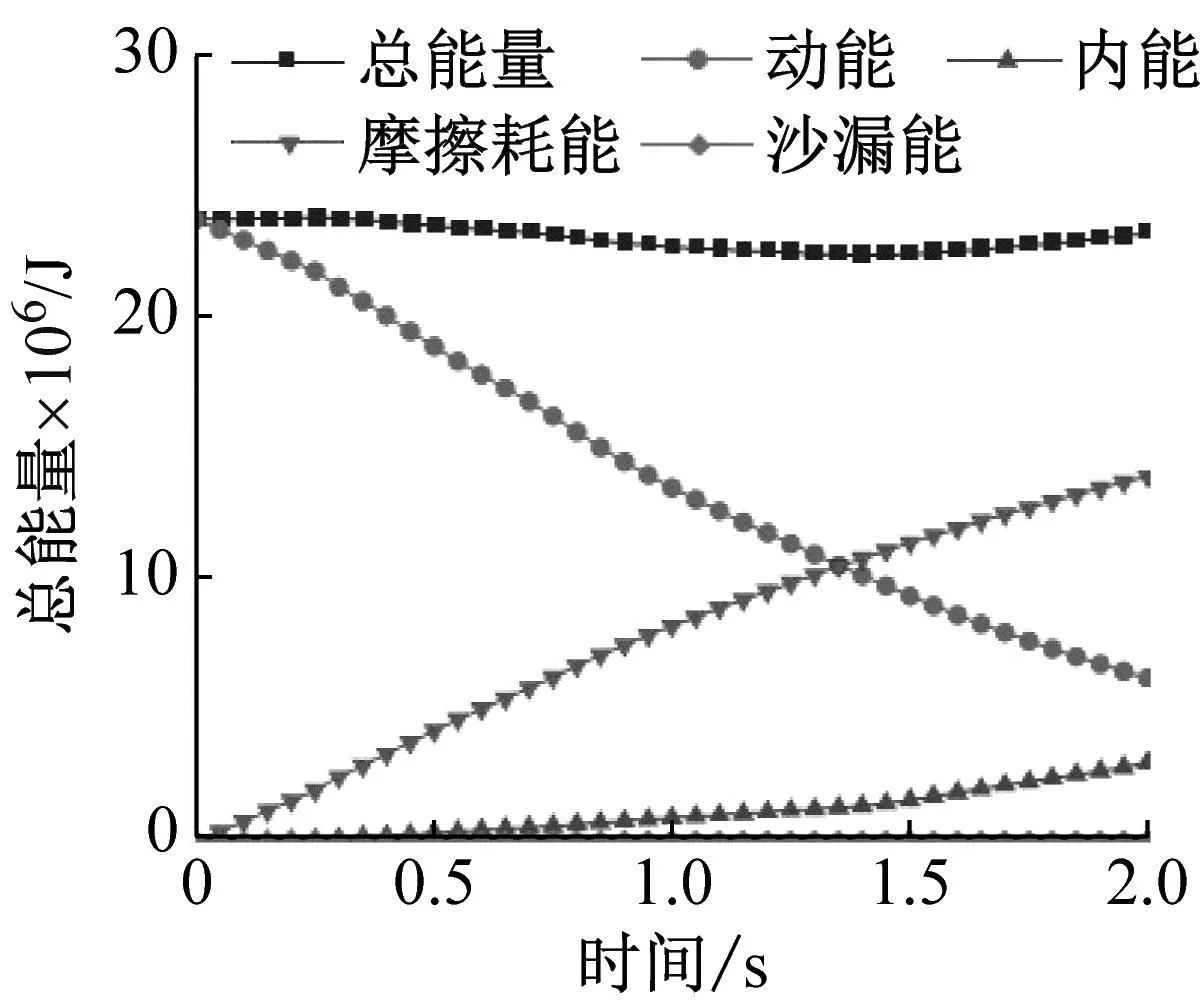
(c) v=10 m/s

4 结 论

通过有限元模拟方法构建框架结构房屋与泥石流耦合数值模型,研究典型框架结构在泥石流冲击作用下的动力响应,得到结论如下：

(1) SPH-FEM耦合的数值方法能够较好地模拟泥石流冲击框架结构时爬高、绕流扩散、淤积稳定等过程,模拟房屋结构的破坏形态与实际泥石流灾毁现场房屋结构受损特征近似,验证了该耦合数值方法和耦合模型的正确性。

(2) 在低等强度泥石流冲击下,框架房屋仅前排填充墙受到破坏,大石块的冲击作用造成前排角柱及其后方侧墙发生局部破坏;在中等强度泥石流冲击下,框架房屋前后两排填充墙受到破坏,大石块和泥石流浆体耦合冲击作用造成角柱及其后方侧墙发生严重破坏,该跨框架整体失稳;在高等强度泥石流冲击下,前后框架柱和墙体遭受严重破坏,整个框架失稳倒塌,致其完全破坏。

(3) 纵向填充墙由于其较低的面外抗弯能力,是最先受损的构件,其临界破坏速度约为3 m/s。框架柱是房屋结构的重要受力构件,房屋倒塌是由框架柱的渐进破坏造成的。大石块的集中作用是框架柱局部破坏的主要原因,在泥石流模型中不可忽略。

(4) 从关键点位移和速度曲线可以看出,框架柱由于泥石流的冲击作用在0.15 s内产生最大变形,之后保持在很小范围内波动。可见泥石流的冲击破坏能力主要来自泥石流龙头的冲击力,龙身冲击力相对于龙头降幅约34.2%。因此房屋结构只要能够抵抗住泥石流龙头的冲击作用,就能够避免整体结构倒塌的危险。

(5) 系统能量主要通过泥石流动能转化为结构内能和摩擦耗能,其中房屋消耗能量较少(17.8%),主要靠泥石流与地面之间的摩擦力和泥石流之间的相互作用耗散能量(82.8%)。