强夯动荷载作用方向对黄土边坡稳定性的影响分析

吴丙权, 倪万魁, 拓文鑫, 任思远, 陈军廷

(1.长安大学 地质工程与测绘学院,西安 710064;2.长安大学 西部矿业资源与地质工程教育部重点实验室,西安 710064)

强夯法是一种加固地基的有效方法[1],它将十几吨至上百吨的重锤,从几米至几十米的高处自由落下,对土体进行动力夯击,使地基承载能力、抗变形能力均达到了工程建设的要求。目前,强夯动荷载作用下地基的稳定性成为学者们研究的热点[2-4]。通过现场实测发现,在同一夯点且夯能相同的情况下,随着夯击数的增加振动加速度峰值大小呈现增加的趋势[5]。Kundu等[6]利用在室内的强夯试验,分析了夯锤直径的大小对地基处理的影响。水伟厚等[7]对高能级(10 000 kN·m)强夯在碎石回填地基上的加速度传播规律及衰减过程进行了研究分析,为地基处理提供了参考。强夯法主要适用于颗粒粒径大于0.05 mm的粗颗粒土,对湿陷性黄土地基的处理效果尤为明显。在施工过程中,强夯影响范围内的土体变形模量逐渐增加,土体的压实度也在增加,黄土的湿陷性也逐渐消除[8]。强夯法处理加固地基作用效果十分明显,但在强夯处理地基过程中,这种工法引起的房屋及周边环境的安全也是工程中经常遇到和需要亟待解决的问题[9-10]。Pourjenabi等[11]利用ABAQUS软件对砂土质地基受到强夯作用下的受力状态进行了三维模拟,分析了夯击振动波的峰值速度及波动加速度对相邻结构的影响,确定了相邻结构之间的安全距离。高能级强夯施工更有可能对周边建筑物的安全和耐久性产生显著的危害[12]。

在强夯动荷载作用下,对边坡的影响问题逐渐受到关注。秦伟华等[13]结合工程实例,分析强夯对填方边坡振动效应的影响,研究发现边坡坡面对水平径向速度有放大作用并呈抛物线衰减,坡顶传播速度呈指数型衰减。在广阔的黄土高原地区,强夯施工的工程项目较为常见。黄土由于其本身的特性,受到复杂环境因素的影响更易于产生滑坡等地质灾害。在强夯振动作用下,黄土坡体原有的约束作用减弱。连续的夯击振动加速了约束作用的改变,使坡体内部的力学关系发生了改变[14],同时减小了土体的摩擦力,降低了黄土体的抗剪切能力,使黄土坡体的安全系数减小,由此引起的黄土边坡滑塌现象也时有发生,因此有必要对强夯荷载作用下的黄土边坡稳定性进行分析。

目前,对强夯作用下黄土边坡的稳定性研究多是对振动波在边坡中的传播机理进行分析,对强夯作用下的边坡稳定性缺少量化评价。边坡的安全系数是评价边坡稳定性的传统方法,而极限平衡法在求解边坡安全系数由于其原理简单、操作方便,在土坡稳定性分析中得到了广泛应用[15]。在其他类型的动力荷载对边坡稳定性分析中,刘华丽等[16]分析了爆破地震动荷载作用下对边坡的稳定性影响,探讨了动荷载加速度方向对边坡安全系数的影响。Terzaghi[17]结合极限平衡理论讨论了地震作用下的边坡稳定性分析。Kramer[18]运用拟静力法分析了地震作用下边坡土体的稳定性,其将动荷载作用力分为水平和竖直方向恒定的惯性力。但实际上地震动荷载作用力是一个动态过程,作用在水平和竖直方向的作用力随着传播方向的改变发生了动态变化。因此,分析动荷载在边坡上的作用时,应考虑其传播方向不同对边坡稳定性的影响。强夯振动加速度产生的作用力会导致边坡失稳,因此有必要分析强夯振动加速度不同的传播方向对黄土边坡安全系数的影响。

本研究采用极限平衡圆弧条分法对强夯作用下的边坡安全系数进行推导计算,把边坡滑体简化为连续的竖向土体条块,将强夯振动产生的力拟为静力作用在条块中,以拟静力系数表达,通过极限平衡分析得出安全系数的计算推导式。在计算安全系数时,采用极限圆弧滑动面搜求法来确定安全系数最小的滑动面为极限滑动面,运用MATLAB编程求出最小安全系数。结合工程实例,使用TC-4850爆破测振仪对现场监测点进行加速度测试。考虑高程差和测点距离的共同影响,采用MATLAB编程对现场数据进行多元回归分析,求出强夯作用下边坡质点振动加速度解析式。最后根据安全系数和拟静力系数进一步分析强夯动荷载作用方向对边坡安全系数的影响,来验证理论推导的合理性。本方法依据传统的极限平衡圆弧条分法,原理简单、易于实现编程计算,可应用于黄土边坡实际工程中。

1 强夯作用边坡稳定性分析

1.1 安全系数求解

采用极限平衡条分法进行分析,这种方法简化为一个滑动土体沿着未滑动土体滑动,只考虑条块的内部受力,忽略条块间的作用力,分析滑面上的极限平衡。根据现场工程实际情况来看,坡体的滑动面呈现出圆弧形滑动,故在强夯作用下,黄土边坡的受力破坏图如图1所示。

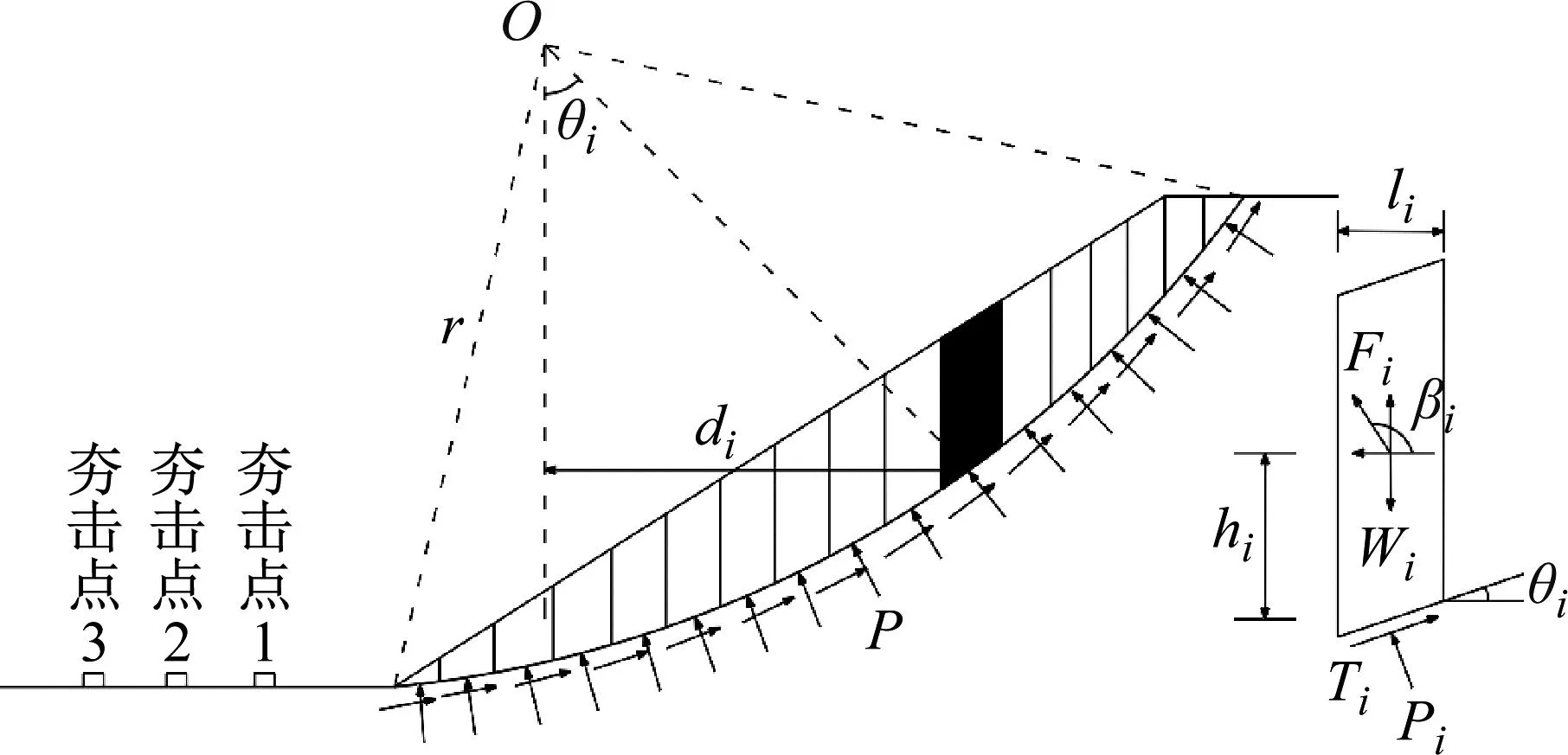
注：Fi为强夯动荷载在土条质心的作用力;βi为强夯动荷载作用方向与水平轴夹角;Wi为土条重度;Ti为土条抗剪切作用力;Pi为作用在土条上的法向支撑力;hi为土条质心高度;θi为土条与水平方向的夹角;r为圆弧半径;di为土条到圆心的作用距离。

将边坡土体离散为n个土条,取某一土条i作为隔离体进行分析,根据滑动面上的极限平衡条件,则有

(1)

式中：Ti为土条抗剪切作用力;Pi为作用在土条上的法向支撑力;Fs为安全系数;ci为土体黏聚力;φi为土体内摩擦角;li为土条底边的长度。

假定条间力的作用力为零,对土条进行分析,考虑径向力的平衡,有

(2)

Fi=Kw·Wi

(3)

式中：Kw为与强夯振动荷载强度关联的拟静力系数;Wi为土条重力;Fi为强夯作用在土条上的力。

所有土条的自质量ΔWi与荷载对圆心O求力矩,作用在土条上的强夯作用力进行水平和竖直方向分解后对圆心O求力矩,则有

ΔWi·di=ΔWi·r·sinθi

(4)

Fi·sinβi·di=Fi·sinβi·r·sinθi

(5)

Fi·cosβi·di=Fi·cosβi·r·cosθi

(6)

当滑动土体处于极限平衡状态时,滑动力矩等于抗滑力矩,则有

(7)

(8)

将式(1)代入式(8),有

(9)

求出安全系数Fs的显式表达式为

(10)

采用MATLAB编程计算强夯作用下黄土边坡的安全系数,在求解过程中运用圆弧滑动面搜索枚举法确定极限圆弧滑动面,对不同半径的滑动面进行稳定性验算,将安全系数最小的滑面视为极限圆弧滑动面,对极限圆弧滑动面进行稳定计算即求出黄土边坡的安全系数。

2 工程实例分析

在黄土高原某工程建设场地,距离边坡的坡脚不远处,利用强夯机械对黄土地基进行处理。边坡情况：坡高H为50 m,斜坡角度α为60°,斜坡总长为57.5 m,夯锤在距离坡脚L=15 m处,强夯施工边坡破坏现场及示意图如图2所示。

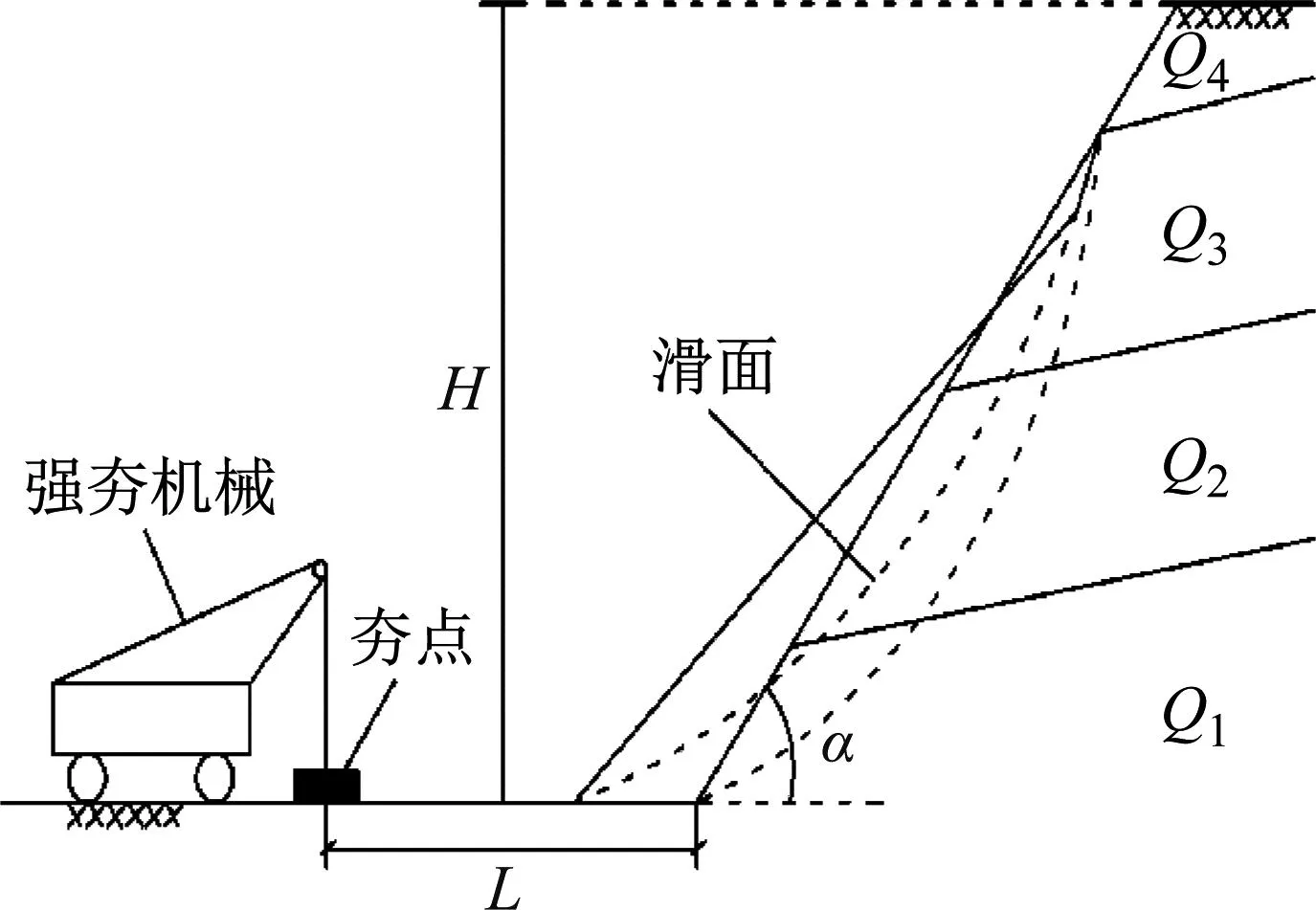
图2 某强夯施工边坡破坏现场及示意图

黄土边坡力学参数如表1所示。强夯参数如表2所示。

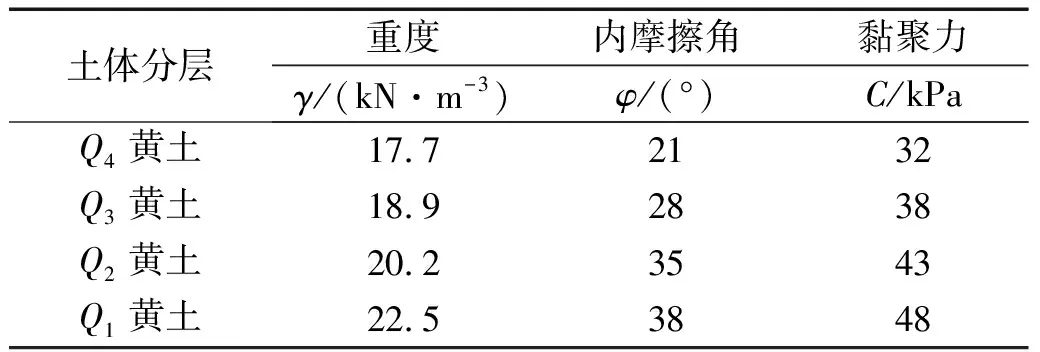
表1 黄土力学参数

表2 强夯参数

现场强夯能级为800 t·m,采用中国地震局TC-4850爆破测振仪对强夯振动加速度进行测试,现场测试如图3所示。

图3 强夯振动加速度现场测试

坡面监测点位布置如图4所示,CD-1布置在坡脚处,CD-2、CD-3、CD-4、CD-5、CD-6、CD-7、CD-8、CD-9根据不同的坡高布置在坡面上。

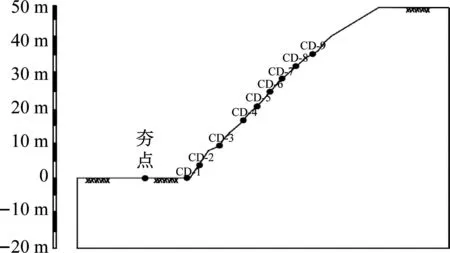
图4 坡面监测点位布置示意图

目前的测试仪器多是三向传感器,分为水平、竖向、径向三个方向,根据波的传播规律,一般测试多为水平和竖向。不同的测试地点有时是水平向最大,有时是竖向最大,这与强夯振动产生的瑞利面波质点运动轨迹有关,根据相关研究,瑞利波沿着介质表面传播,介质的质点运动轨迹为椭圆[19-20]。因此测试仪器所放地点测试出的加速度大小,按照最后一击测试结果取值,并且取测试最大值,测试结果如表3所示。

表3 不同监测点位强夯振动加速度

根据现场夯击试验,随着夯锤数的增加,夯击产生的振动也在增大,因此在进行强夯对黄土高边坡的振动评价时,采用最后一次夯击的振动幅值作为计算数值。因此,强夯动荷载拟静力系数中振动加速度为最后一次夯击产生的加速度为准,强夯动荷载拟静力系数如式(11)所示。

(11)

式中：Kw为拟静力系数;a为强夯振动加速度;g为重力加速度。

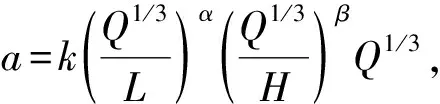
根据现场测试数据,采用MATLAB编程对加速度a进行多元回归分析,得出强夯加速度的解析式,如式(12)所示

(12)

将a代入式(14),可以求出拟静力系数Kw。

按照振动波在传播过程中对坡面最不利的情况考虑,分析坡面上与夯击点距离为20、25、30、35、40、45、55、60、65、70 m处拟静力系数。依据Kw的计算公式,结果表4所示。

表4 不同坡面点拟静力系数

坡面上不同监测点同坡高、夯击点距离拟静力系数变化趋势如图5所示。

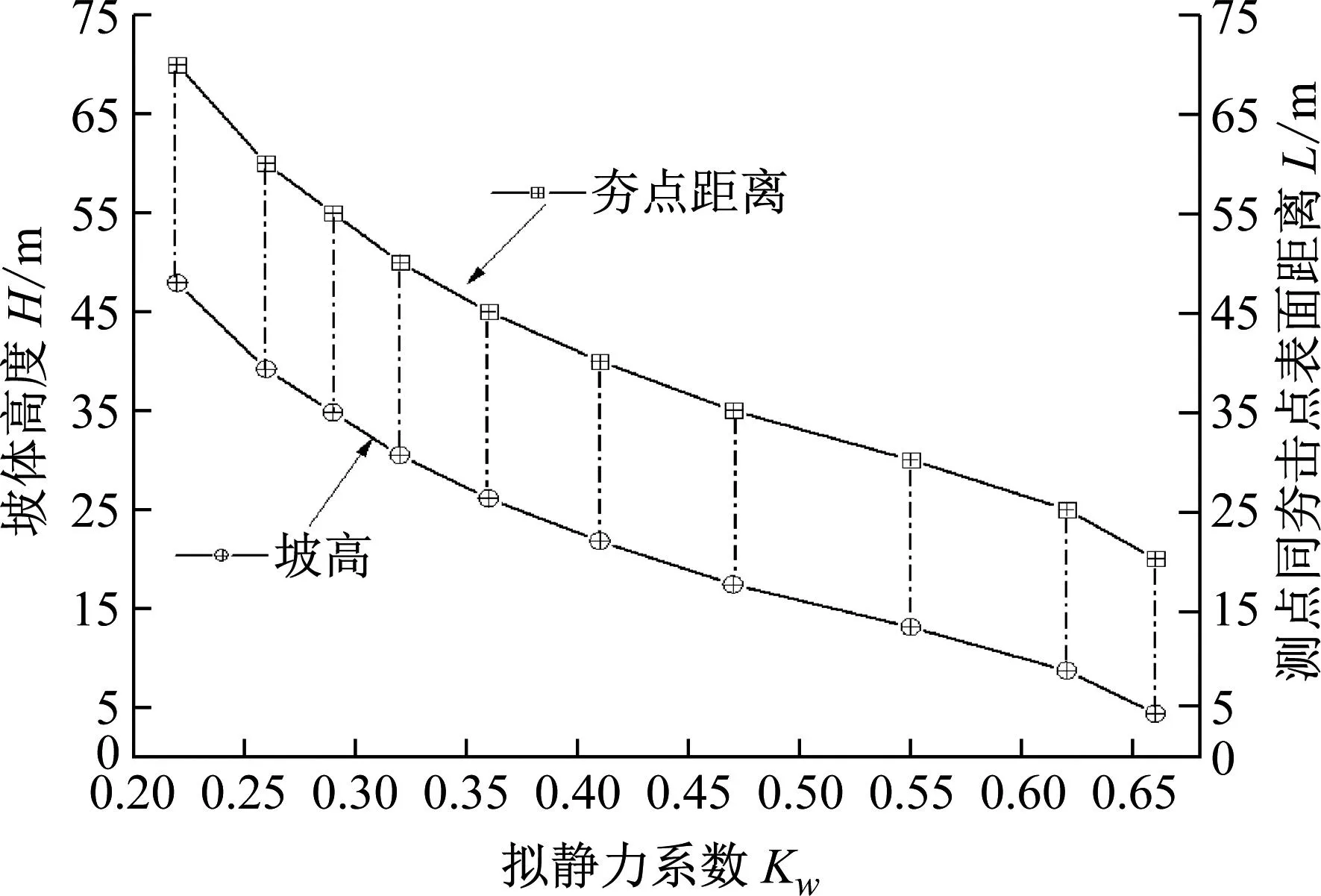
图5 拟静力系数变化趋势

从拟静力系数的变化来看,随着坡高的降低,拟静力系数逐渐变大;坡面上与夯击点距离越远,拟静力系数越小。在坡面上,随着距离或者坡高的增加,拟静力系数大小逐渐降低,坡高和离夯击点的距离等因素对拟静力系数有着相似规律的影响。

3 动荷载方向对安全系数影响

结合现场实际和计算情况,强夯作用在滑面上的作用力,本研究计划用拟静力法将动荷载转化为静荷载。在800 t·m作用下,夯机距离坡脚15 m处,拟静力系数变化范围主要在0～0.70区间。在区间0.35～0.70拟静力系数对边坡的影响趋势同区间0～0.35一致,可选取拟静力系数0.10～0.35区间分析对边坡的影响。因为强夯振动产生的加速度为矢量,矢量的属性决定了边坡稳定性计算时必须考虑强夯动荷载方向。因此假设强夯动荷载方向与水平轴正方向夹角为β,0°≤β≤360°,在确定的坡高坡度情况下,运用圆弧条分法分析强夯动荷载方向和拟静力系数对圆弧形滑坡最小安全系数Fs的影响。分别采用拟静力系数Kw=0.35、Kw=0.30、Kw=0.25、Kw=0.20、Kw=0.15、Kw=0.10、Kw=0.04来进行分析,根据安全系数计算公式(10),利用MATLAB程序编程计算结果如图6所示。

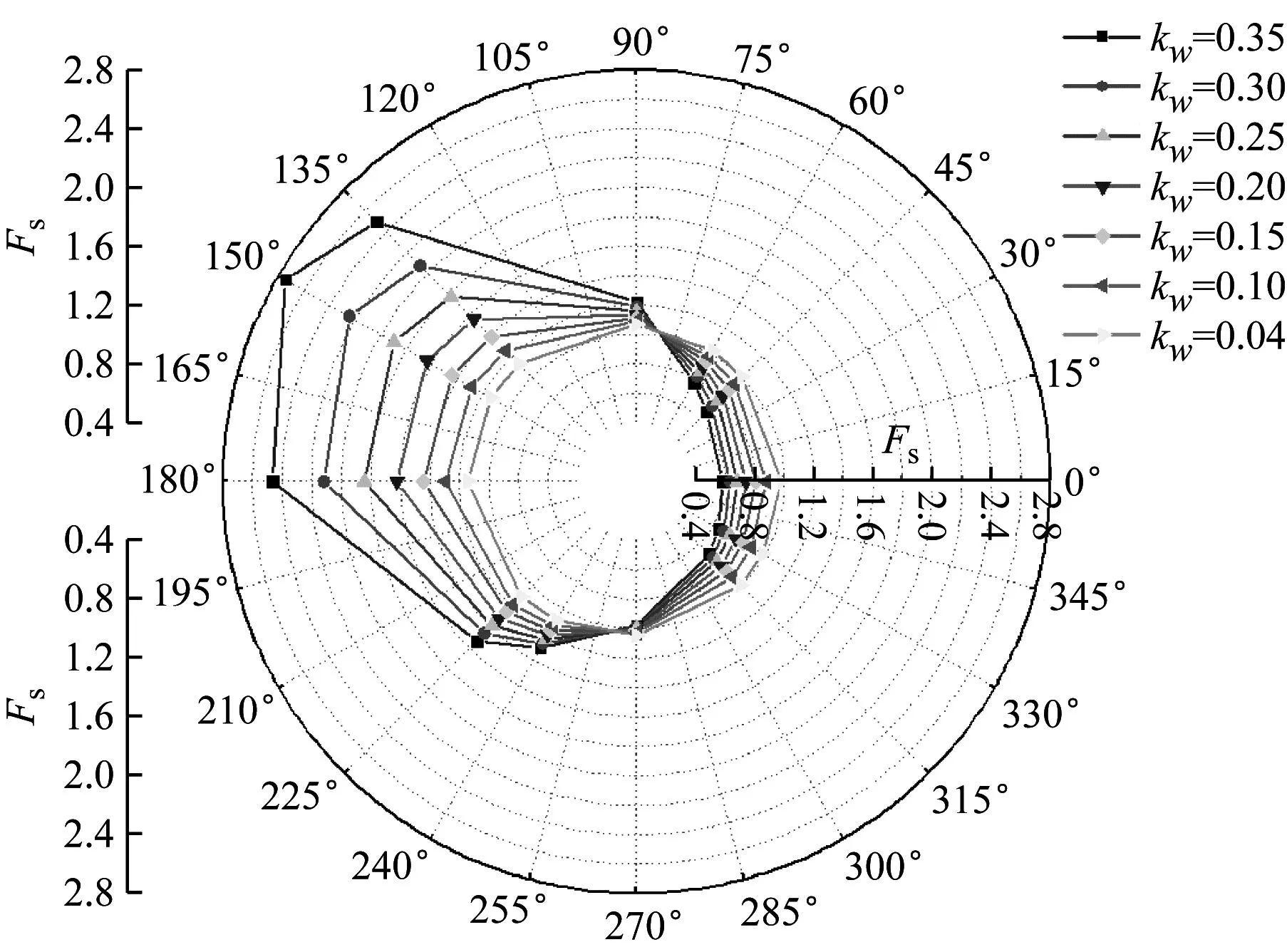
图6 安全系数变化图

由图6可知,当强夯动荷载方向与水平轴正方向夹角为0°时,随着拟静力系数的增大,安全系数逐渐减小且均小于1.00,坡体处于不稳定状态,即滑坡失稳状态;随着强夯动荷载与水平轴正方向夹角增大到80°时,安全系数逐渐增加,但均小于1.00,坡体处于不稳定状态。夹角从75°增加到90°时,安全系数变化较为明显,拟静力系数越大,安全系数呈现出增大趋势,且在夹角为80°时,安全系数趋近于1.00。在夹角为90°时,坡体安全系数已大于1.05,此时坡体整体趋于稳定。

强夯动荷载方向与水平轴正方向夹角为90°～150°时,坡体安全系数随着拟静力系数和夹角度数的增加而逐渐增大,且均大于1.05。当夹角为135°～150°时,安全系数最大值已大于2.6,说明这个方向的角度对于坡体的安全稳定性是有益的,强夯振动反而促进和保证了坡体的安全稳定。当夹角增加到150°～180°时,坡体安全系数随着拟静力系数和夹角度数的增加有逐渐减小的趋势,但坡体总体处于稳定状态,安全系数均大于1.05。随着夹角的继续增加,当夹角为180°～270°之间时,坡体安全系数的大小随着夹角度数的增加有加速减小的趋势,但坡体安全系数总体上大于1.05。当夹角为270°时,安全系数小于1.00,坡体处于失稳状态。当夹角为270°～360°时,安全系数均小于等于1.00,坡体处于失稳状态。

综上所述,在强夯动荷载方向与水平轴正方向夹角为0°、45°、60°、270°、315°、330°、360°时,随着拟静力系数不断增大,安全系数会越来越小,边坡的稳定性越差,且安全系数均小于等于1.00,边坡出现滑塌现象。在强夯动荷载方向与水平轴正方向夹角为90°、135°、150°、180°、225°、240°时,随着拟静力系数不断增大,安全系数也随之增大,边坡的稳定性性较好。安全系数均大于等于1.05,边坡的稳定性较好。不同的强夯动荷载方向能够导致黄土边坡受到的荷载作用力、下滑力、摩擦阻力以及潜在滑移面产生的抗剪强度有着明显不同,因此对边坡的稳定性影响也不同。

当边坡安全系数小于1.00,在强夯动荷载方向与水平轴正方向夹角为0°、45°、60°、270°、315°、330°、360°时,对强夯荷载作用在坡体土条上的拟静力Fi进行分解,在土条质心处分解成竖直作用力和水平作用力。分析发现分解后的竖直和水平作用力不能增加土条的稳定性,反而加速了土体的下滑,从而使得整个边坡滑塌破坏。拟静力Fi的分解如图7所示。

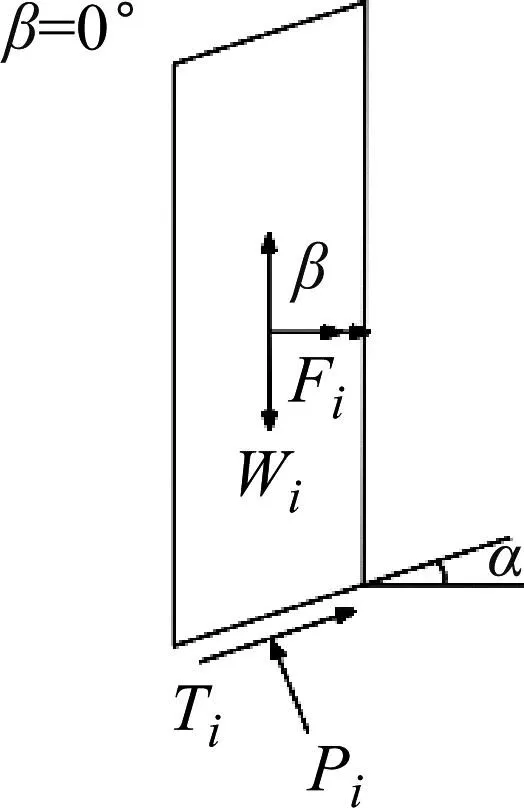
图7 Fs≤1.00时不同角度强夯作用力在土条上的分解图

当边坡安全系数大于1.00,强夯动荷载方向与水平轴正方向夹角为90°、135°、150°、180°、225°、240°时,对强夯荷载作用在坡体土条上的拟静力Fi进行分解,在土条质心处分解成竖直作用力和水平作用力。分析发现分解后的竖直和水平作用力能够增加土条的稳定性,反而进一步加固了边坡,使得边坡更加安全稳定,拟静力Fi的分解如图8所示。

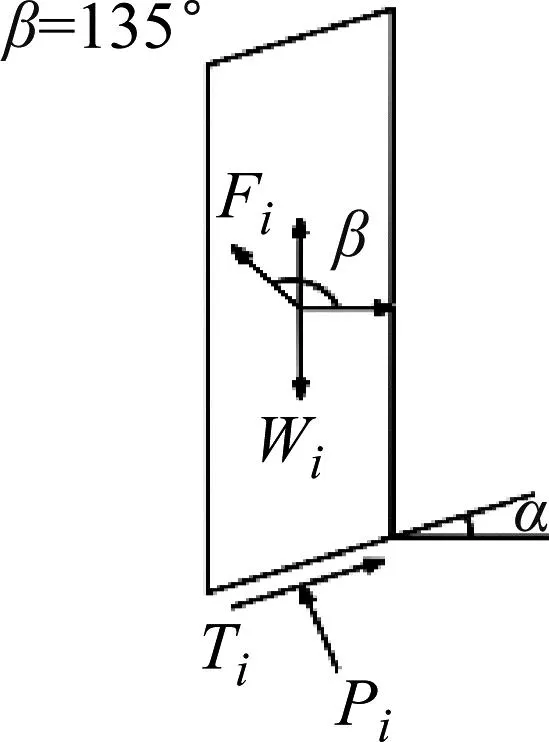
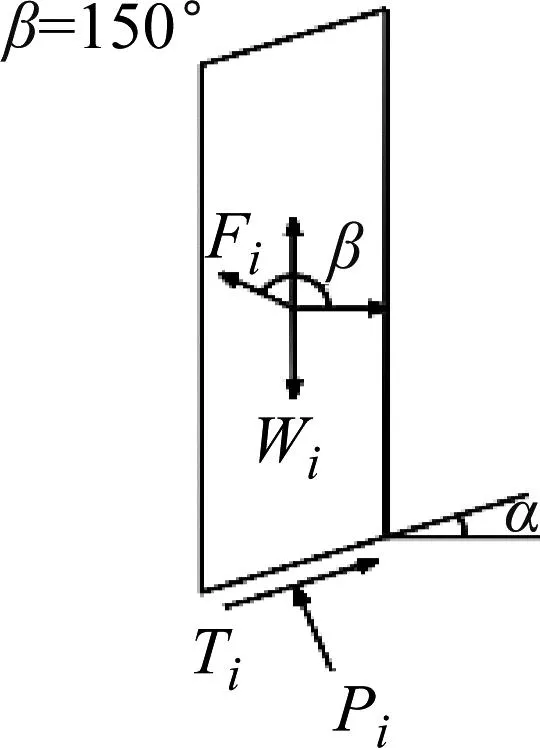
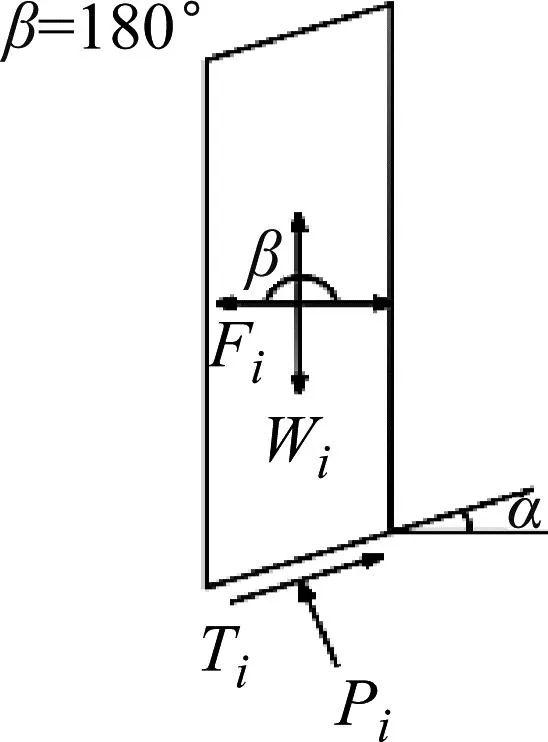
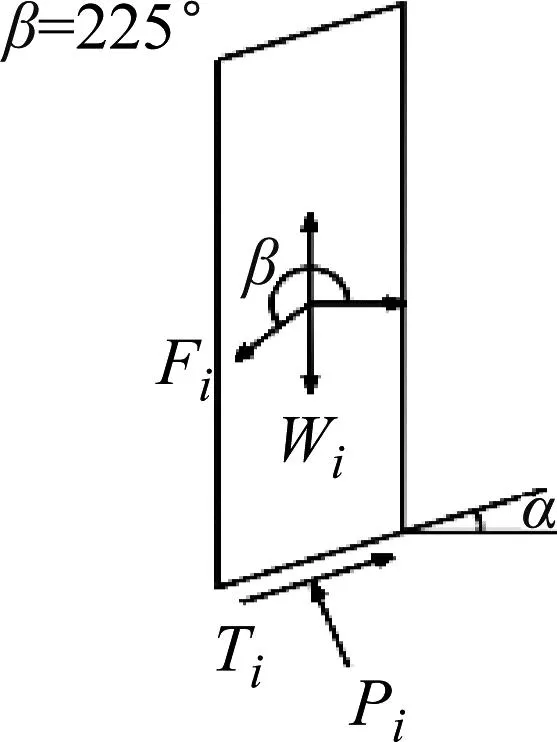
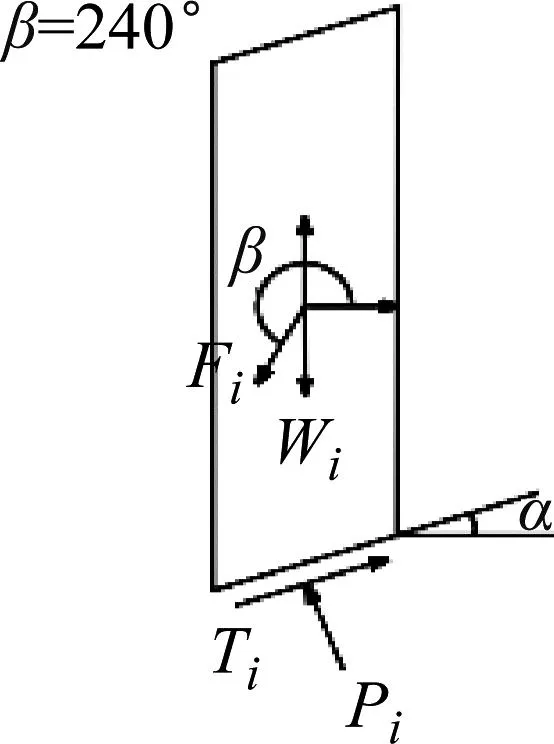
图8 Fs>1.00时不同角度强夯作用力在土条上的分解图

同时根据DBJ 61/T 192—2021《湿陷性黄土地区边坡工程勘察规范》[23],当边坡稳定性系数Fs<1.00时,此时边坡不稳定;当边坡稳定性系数1.00≤Fs<1.05时,边坡处于临界状态,即欠稳定状态;当边坡稳定性系数1.05≤Fs,且大于边坡稳定安全系数Fst时,边坡处于稳定状态。根据拟静力系数、强夯动荷载方向与水平轴正方向夹角以及安全系数之间的关系可知,分析结果符合规范要求。

4 结 论

本文采用极限平衡圆弧条分法对黄土边坡的安全系数进行推导计算,结合工程实例,分析了强夯振动加速度不同方向对边坡稳定性的影响。通过研究分析,我们得出以下结论：

(1) 根据现场工程实际情况来看,坡体的滑动面呈现出圆弧形滑动。采用极限平衡圆弧条分法分析坡体的安全系数,得出在强夯荷载作用下边坡的安全系数Fs计算公式,此方法在分析强夯作用下的边坡稳定性时原理简单,求解程序易于实现。

(2) 同时考虑坡高和夯击点距离的影响,采用MATLAB编程对现场数据进行多元回归分析,求出强夯振动加速度解析式。依据强夯拟静力系数计算结果,分析拟静力系数同坡高和测点同夯击点表面距离的关系。结果表明在坡面上,坡高和离夯击点的距离等因素对拟静力系数有着相似规律的影响。

(3) 在强夯动荷载方向与水平轴正方向夹角为0°、45°、60°、270°、315°、330°、360°时,随着拟静力系数不断增大,安全系数越来越小,且安全系数均小于等于1.00;在强夯动荷载方向与水平轴正方向夹角为90°、135°、150°、180°、225°、240°时,随着拟静力系数不断增大,安全系数也随之增大,且安全系数均大于1.05,结果显示出不同的强夯动荷载作用方向对坡体的稳定性所起效果不一致。本方法依据传统的极限平衡圆弧条分法,原理简单、易于实现编程计算,可应用于黄土边坡实际工程中。