轨道车辆一系螺旋弹簧振动疲劳失效分析

孙文静, 王嘉豪, THOMPSON David, 王腾飞, 周劲松

(1.同济大学 铁道与城市轨道交通研究院,上海 201804;2. Institute of Sound and Vibration Research, University of Southampton, Southampton SO17 1BJ, UK)

螺旋弹簧作为重要的弹性隔振元件,在高铁与地铁等列车的一系悬挂系统中广泛使用,是保证车辆运行安全性和乘坐舒适性的关键部件[1]。但各类轨道车辆在服役工况下螺旋弹簧疲劳断裂故障时有发生,对列车运行安全性与经济性产生不利影响。

某些线路上轨道车辆的一系螺旋弹簧断裂多达几百次,经观察统计其断裂主要包括由于高接触应力及簧条内圈高应力引起的两种失效方式,且断裂大多位于弹簧1～2圈之间[2-4],如图1所示。目前关于接触疲劳断裂的研究较多,王文静等[5]针对某高速列车轴箱弹簧,将线路载荷测试结果作为输入,采用有限元模型分析,结果表明弹簧第一有效圈与端圈产生较大的接触应力是导致弹簧断裂的主要原因。Wang等[6]针对机车螺旋弹簧研究,结果表明其支撑圈与第一有效圈存在明显的不均匀接触线引起疲劳断裂。除此以外,由簧条内侧裂纹萌生扩展引起的疲劳断裂也较为普遍,在某线路地铁一系断簧故障中,其1～1.6圈处断簧裂纹源于簧条内侧的占比达40%以上[7],断口形状如图1(b)所示,但相关研究相对较少。

(a) 簧条接触疲劳

(b) 簧条内侧疲劳

目前,国内外螺旋弹簧设计主要依据EN13906标准[8]及弹簧手册[9],根据额定静载荷计算最大应力用于疲劳强度分析,忽略了高频激励下弹簧自身动态特性影响。轨道车辆采用的螺旋弹簧结构质量与几何参数均较大,运行时在宽频的轮轨系统随机激扰下,弹簧内部由于波动效应引起动刚度特征[10],在相同振动激励下作用力增大,这对系统隔振和弹簧自身抗疲劳性能不利。文献[11-12]分别分析了由于车轮多边形与钢轨波磨引起一系螺旋弹簧断裂故障。目前关于螺旋弹簧疲劳失效的研究,较多集中在材料及制造工艺分析上[13]。虽然提高材料品质对延长弹簧寿命来说十分重要,但通过断簧检查发现大多满足材料与工艺要求[14]。簧条内侧高应力断裂,断口表现为显著的交变载荷作用引起的疲劳失效。近年来国内外开展了一些关于轨道车辆一系螺旋弹簧的振动疲劳研究,如Zhou等[15]为了获得某一系弹簧的异常振动原因,建立了多种复杂程度不同的动力学模型,得出是由P2共振力及钢轨波磨引起的结论。周新建等[16]基于多体动力学建立快速地铁车辆动力学模型,模拟了一系钢簧在不同激励状态下的振动,对比不同轨道不平顺及车轮不圆度对弹簧振动影响。

综上所述,考虑服役状态轮轨激励下的一系螺旋弹簧实际振动状况,对准确分析其疲劳性能十分重要。但上述文献未对弹簧动应力响应特性及疲劳寿命进行分析,无法揭示轨道车辆一系螺旋弹簧断裂的共性问题及失效机理。因而,本文针对上述螺旋弹簧振动疲劳断裂问题,以某最高运行速度120 km/h的地铁B型车辆为研究对象,提出基于频域疲劳分析方法,探究其一系螺旋弹簧疲劳失效机理。建立包含螺旋弹簧动态特性的精细化一系悬挂模型,分析服役状态轮轨宽频激励下一系螺旋弹簧内部结构振动与动应力响应,识别弹簧疲劳薄弱位置及断裂原因,为减少服役工况下该类型断裂故障提供依据。

1 螺旋弹簧动态特性分析

1.1 模态分析

轨道车辆的一系悬挂系统通常采用两个同心且旋向相反的内、外金属螺旋弹簧,并联形成弹簧组,螺旋弹簧组的几何与力学特性参数,如表1所示。基于此,首先建立弹簧组的有限元模型,其中内弹簧共37 506个实体单元,外弹簧共35 569个实体单元。

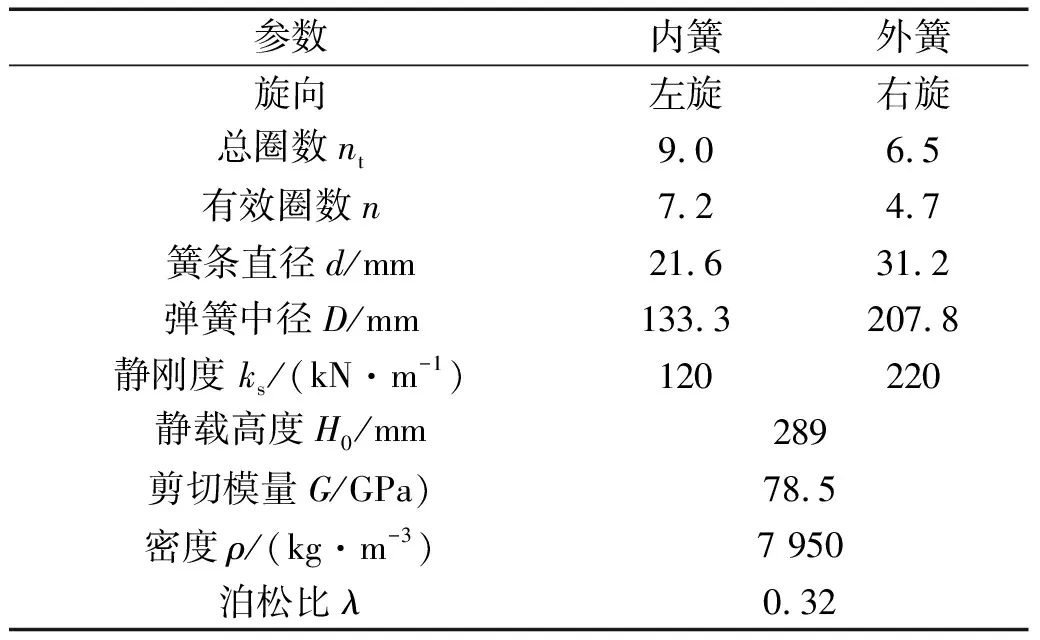
表1 螺旋弹簧组几何与力学特性参数

施加车辆静载模拟螺旋弹簧组在一系悬挂系统中的安装状态,为了分析螺旋弹簧自身动态特性,首先进行模态分析,计算模态振型与模态应力。约束条件下,弹簧组各阶模态频率对应于其动刚度峰值频率[17]。模态振型是每阶固有频率下的结构变形模式,内、外弹簧在100 Hz以内分别包含4阶与5阶模态振型,其模态频率及振型结果,如表2所示。

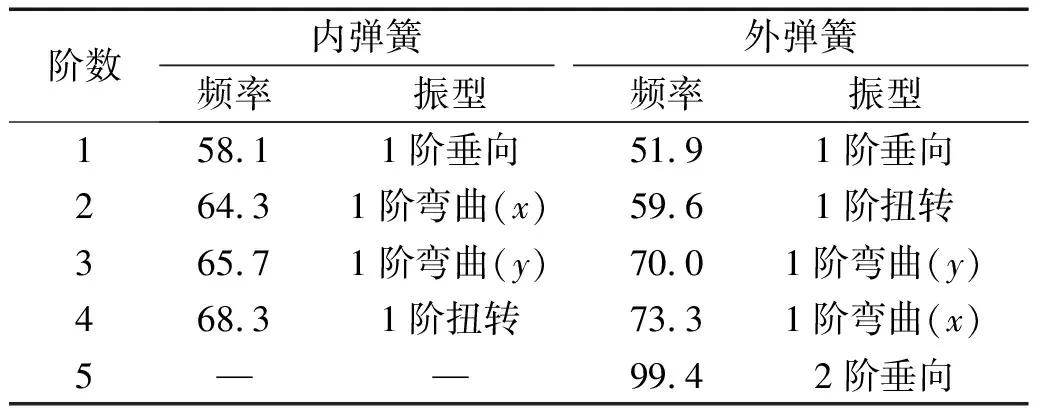
表2 内、外弹簧模态频率

而模态应力与模态振型的相对概念一样,它表征结构各点应力的比例关系。对发生疲劳断裂的内簧进行具体分析,前4阶模态的簧条振动变形及应力分布云图,如图2所示。

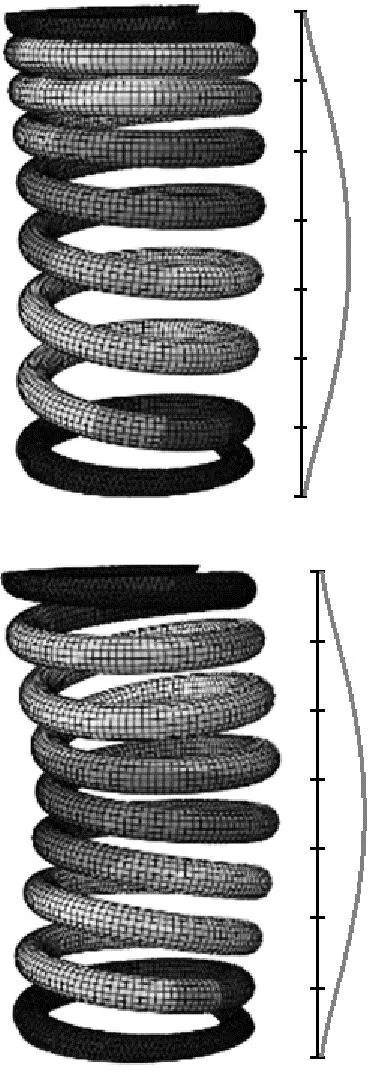
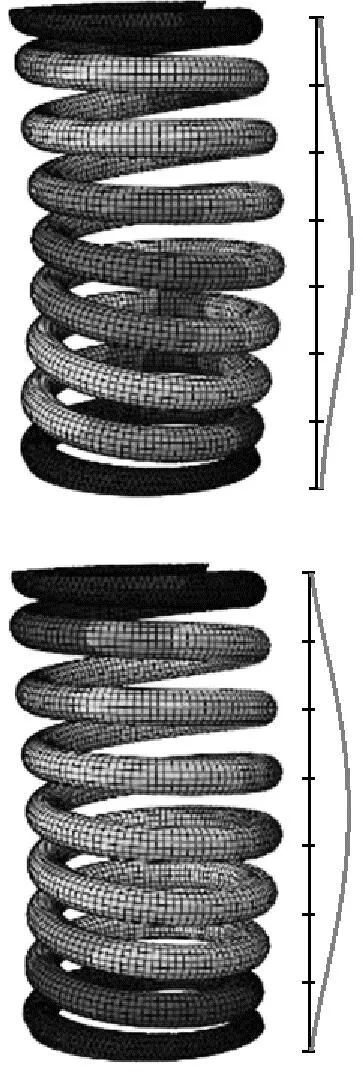
(a) 振动分布

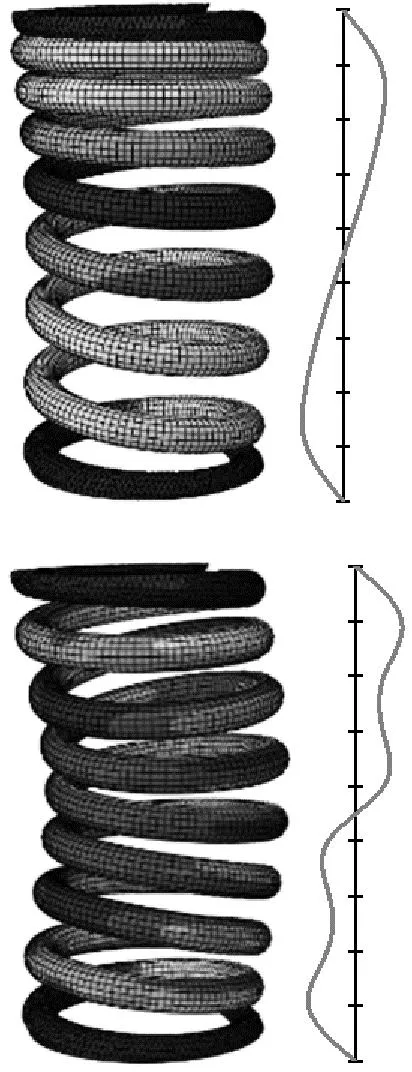
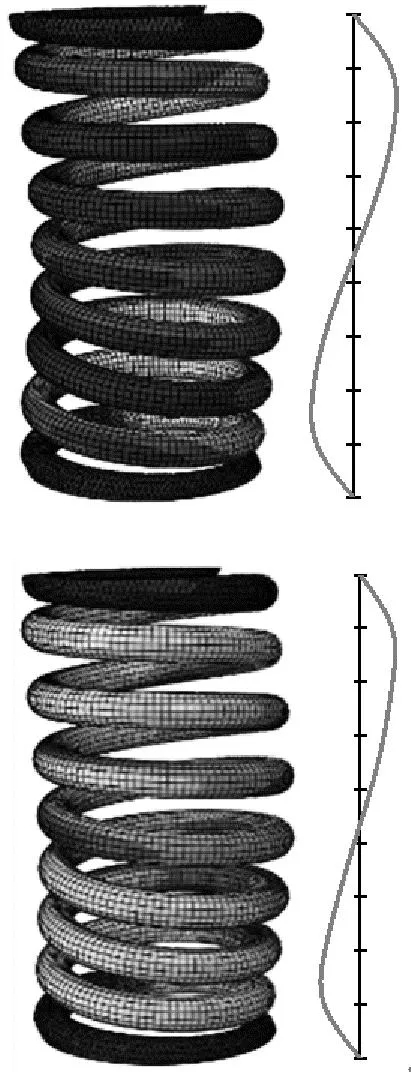
(b) 应力分布

图2中右侧的曲线表示沿簧条内侧位置的振动与应力大小。由图2(a)可见,前4阶模态的最大振动均发生于弹簧中部,向弹簧两端延伸逐渐减小。图2(b)为对应的模态应力云图,模态应力表现出与模态振型不同的趋势,各阶最大模态应力均发生在簧条内侧的1～2圈之间,而模态振动最大的中间位置对应的模态应力则为最小。由此可见,各阶模态频率下振动较小的1～2圈位置,尤其是在1.2圈附近,簧条产生应力集中现象。本文研究的一系内螺旋弹簧断裂多发生于1.2圈处,因而选取该位置进行动应力计算与测试分析。

1.2 螺旋弹簧频响特性

为了获得服役状态螺旋弹簧的动态响应,对螺旋弹簧组进行频响计算。首先,约束弹簧上端,在0～100 Hz进行扫频,采用单位位移激励弹簧下端,计算内、外簧的结构振动及动应力频响。内、外簧中间位置的振动频响如图3所示。由图3可见,在低频时簧条振动与下端的激励接近,弹簧内部跟随激励准静态均匀变形,而随着激励频率增大,弹簧内部出现振动峰值,与表1各阶模态频率完全吻合,在第1阶模态处响应为最大,且内簧在55～70 Hz的振动幅值显著高于外簧。

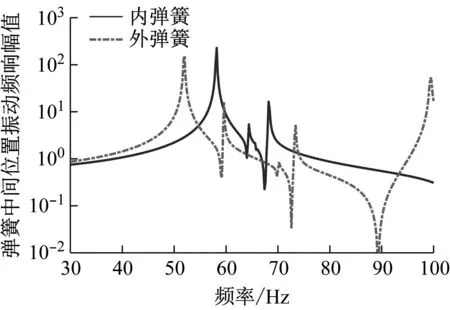
图3 内、外簧中间位置振动频响比较

对单位激励下内、外簧的1.2圈位置动应力频响进行计算,结果如图4所示。弹簧各阶模态频率处均出现动应力峰值,与上述振动峰值频率一致,且第一阶动应力响应最大。

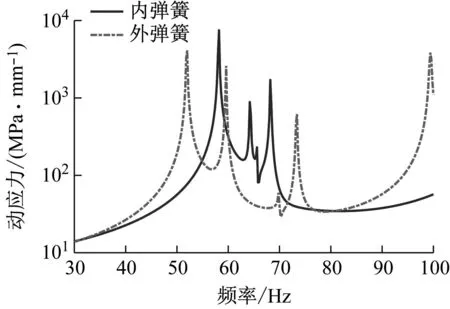
图4 内、外簧1.2圈处动应力频响比较

2 螺旋弹簧服役状态动应力分析

2.1 车辆-轨道耦合系统精细化模型

首先,建立包含轴箱转臂结构(包括转臂橡胶节点)、液压减振器、螺旋弹簧组及簧下橡胶垫构成的一系悬挂系统模型,该模型不仅考虑每个元件的具体位置及其弹性与阻尼参数,同时也包含了螺旋弹簧的动刚度特性,如图5所示。一系悬挂系统参数如表3所示。

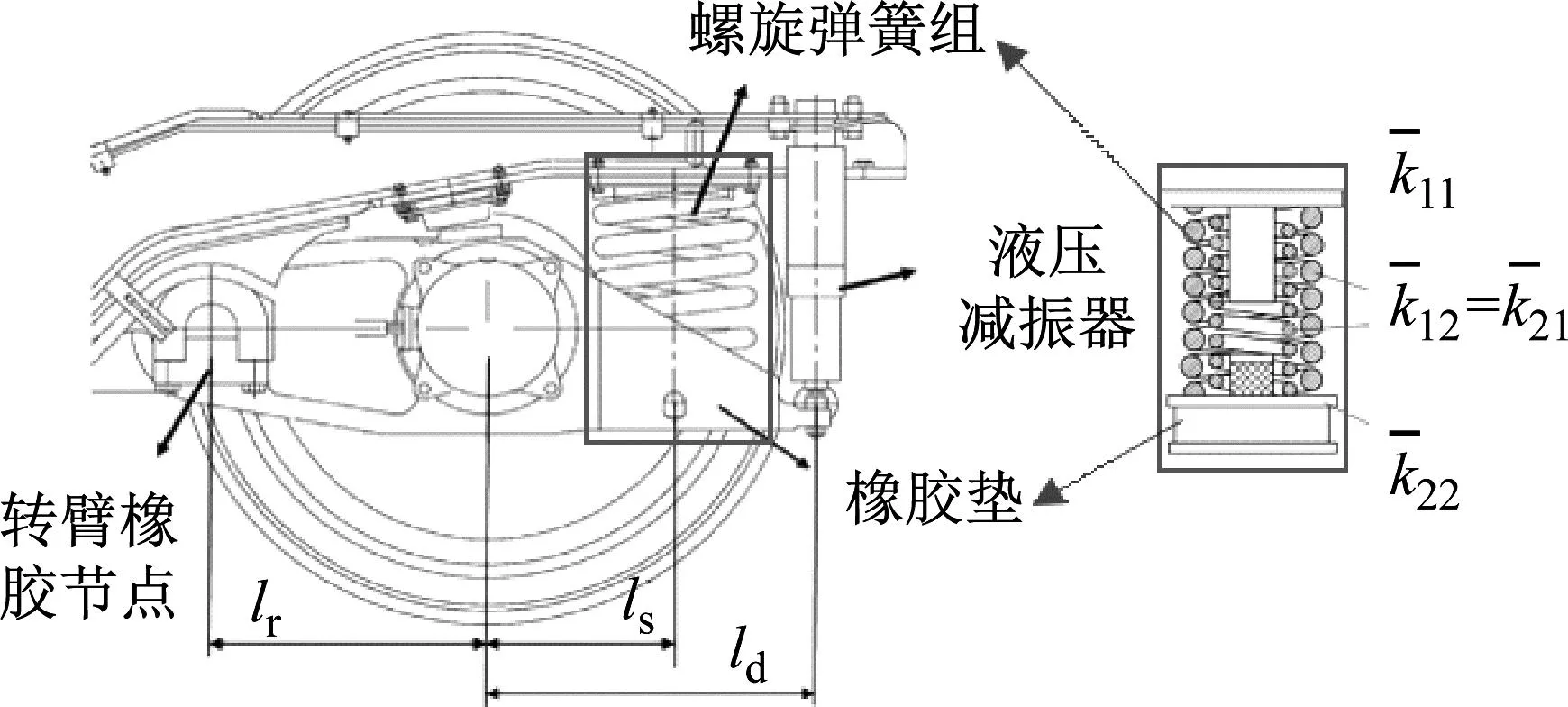
图5 一系悬挂系统结构模型

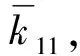
表3 一系悬挂系统参数

由图6可见,该弹性组合系统的动刚度峰值频率与内外弹簧的模态频率保持一致,其两端传递刚度总体上显著高于该组合的设计静刚度值。

将上述包含动刚度特性的精细化一系悬挂模型引入车辆-轨道耦合动力学系统中,如图7所示。kr为转臂橡胶节点刚度,cs1与kd分别为一系液压减振器的阻尼系数与节点刚度,lr、ld、ls分别为转臂节点、液压减振器与弹簧橡胶组距离轴箱中心的距离。轨道为采用普通扣件整体道床的板式轨道结构,轨道垫刚度kp为60 MN/m,轨枕间距ds为0.6 m。

图6 螺旋弹簧橡胶垫组合动刚度

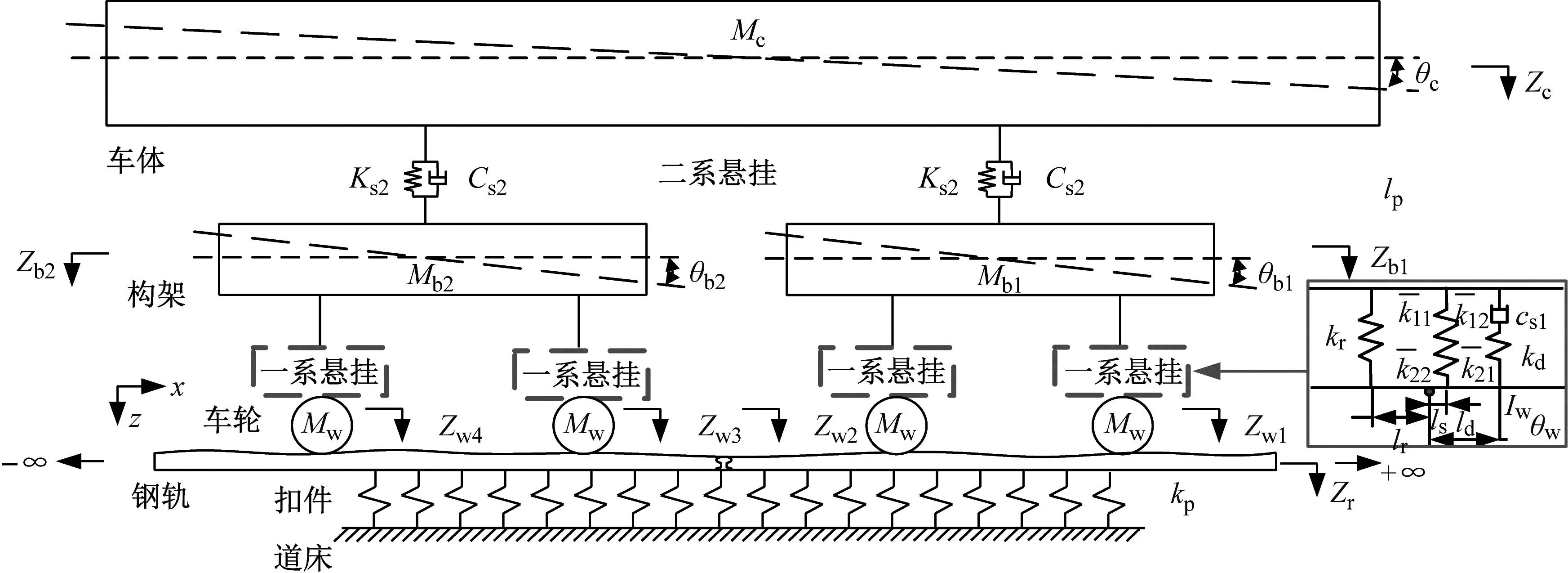
图7 包含螺旋弹簧动刚度特性的车辆-轨道耦合动力学模型

轨道车辆的垂向动力学方程,如下

(1)

式中：M,C与K分别为车辆系统的质量、阻尼及刚度矩阵;Z为14个自由度向量,包含车体、2个构架及4个车轮的垂向自由度,车体、构架及4个轴箱转臂的转动自由度;F为力向量。钢轨视为Timoshenko梁,钢轨弯曲刚度为6.45 MN·m2,采用典型的单层连续支撑地铁轨道模型,支撑刚度s如下

(2)

式中,kp为轨道垫刚度,N/m;ds为轨枕间距。基于格林函数法[18],以美国轨道5级谱[19]作为激励,计算运行速度100 km/h时这一典型工况下的弹簧橡胶垫组合在构架与转臂处的振动加速度功率谱密度结果,如图8所示。

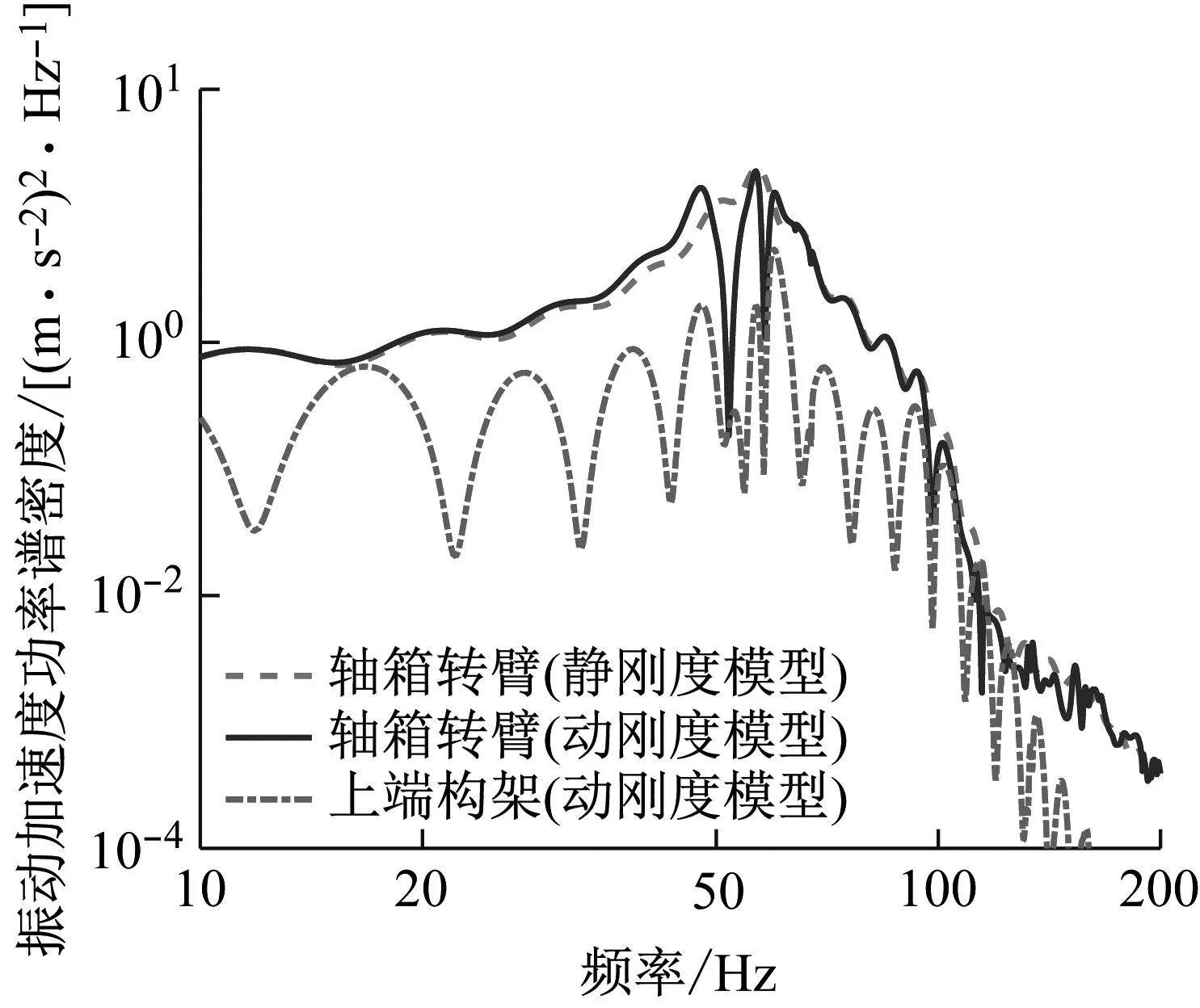
图8 振动加速度功率谱密度

本文所研究的车辆与轨道结构与文献[20]中相同,图8中加入传统静刚度模型结果进行对比,可见轴箱转臂在60 Hz附近具有振动峰值,是由普通扣件整体道床的轮轨P2共振引起。由于内簧与外簧自身模态,在52 Hz与58 Hz的弹簧力与转臂节点力的相位差关系,降低了该频率下的轴箱转臂与构架振动,但由于共振在该频率下螺旋弹簧内部振动剧烈。

2.2 螺旋弹簧两端动载荷计算

对连接构架与轴箱转臂的内外簧与橡胶垫组合两端进行受力分析,如图9所示。

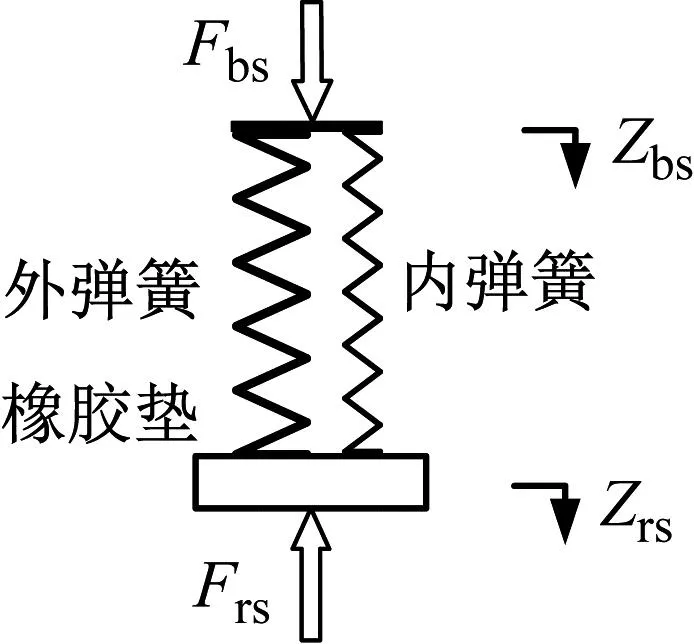
图9 弹簧橡胶垫组受力示意图

依据两端位移及刚度关系,计算弹簧橡胶垫组合上端受力Fbs及下端受力Frs如下

(3)

将2.1节计算得到的弹簧橡胶组合两端的构架及轴箱转臂处的振动响应zbs、zrs与动刚度代入上式,计算得到两端作用力功率谱密度,如图10所示。弹簧橡胶组合若采用传统静刚度模型则两端受力相同,但实际上由于弹簧内部波动效应,考虑动刚度的结构两端受力有所不同,30 Hz后高频动载荷显著大于传统静刚度模型,内、外簧在58 Hz与52 Hz附近由于自身模态的作用力峰值较为显著。

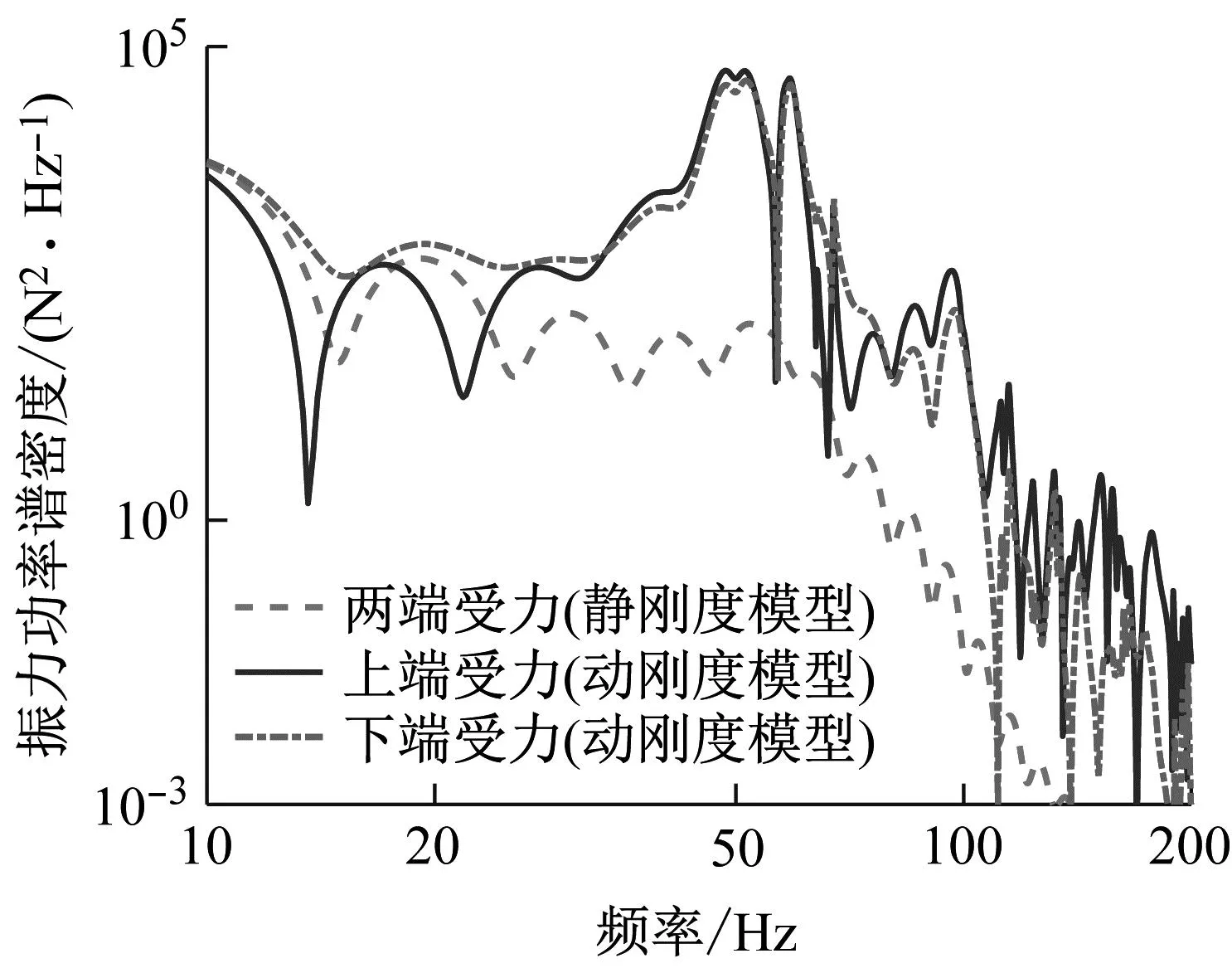
图10 弹簧橡胶垫组合两端受力功率谱密度

2.3 动应力计算

首先依据弹簧手册分析其切应力,弹簧组中的外弹簧具有较大的弹簧中径D及簧条直径d,其静刚度及疲劳强度均大于内弹簧。螺旋弹簧的最大切应力由下式可得

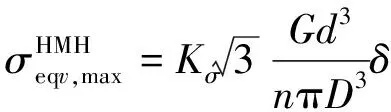
(4)

式中：Kσ为应力修正系数;δ为弹簧上下两端相对变形。内、外簧由于并联,其两端相对变形δ相同,依据表1中内、外弹簧中径与簧条直径大小、有效圈数可知,内簧最大切应力比外簧高出24%。

将2.2节中获得的弹簧两端载荷作为输入,在弹簧有限元模型中进行加载,计算得到该工况下弹簧动应力结果。在车辆一系内簧的1.2圈处粘贴应变片,选取车辆在以时速100 km/h经过普通扣件整体道床区间时,该弹簧位置的动应力测试结果。模型计算与测试条件保持一致,将上述计算结果与测试结果进行对比如图11所示。

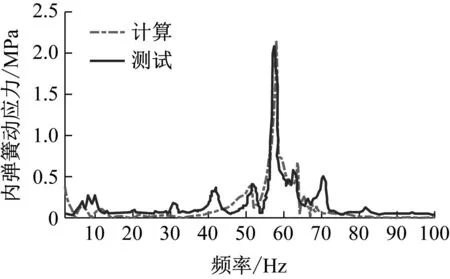
图11 内簧动应力计算与测试结果对比

由图11可见,模型计算与实测结果吻合(应力最大值误差仅为3%),结果表明考虑弹簧动态特性的精细化动力学模型能够较为准确地模拟服役状态下弹簧动应力响应。弹簧在一阶垂向模态频率58 Hz附近的动应力响应最大为2.2 MPa,该处动应力是其它频段应力峰值的3倍以上。根据Miner法则及弹簧材料S-N曲线,动应力增加3倍,结构疲劳损伤增加35倍,5为材料S-N曲线的幂。由此可知,在弹簧的一阶垂向模态频率处的较大的动应力响应,是引起内弹簧在1.2圈位置振动疲劳失效的主要原因。

除此之外,图11中还存在多个实测的动应力峰值,测试时该车辆运行速度v为100 km/h左右,车轮直径dw为0.84 m(新轮),车轮1阶多边形形成的激励频率f为

(5)

由图11可见,测试结果在10.5 Hz、21 Hz、31.5 Hz、42 Hz、52.5 Hz及63 Hz附近应力峰值与车轮1～6阶多边形激励频率相对应,反映了该车辆存在不同程度的多阶不圆,从而引起一系列倍频的应力峰值。而内簧的58 Hz最大动应力峰值与车轮多边形无关,而是由于轮轨P2共振频率与内簧自身一阶模态频率接近。

3 螺旋弹簧结构疲劳分析

轨道车辆服役环境下,螺旋弹簧承受随机动载荷,产生动应力。传统基于静载荷的评估方法(如GOODMAN曲线图)无法考虑结构动应力特性,不适用服役环境下弹簧疲劳寿命分析。基于此,本文采用动强度频域分析弹簧疲劳寿命,即利用上节得到的构架与轴箱转臂对弹簧两端的载荷功率谱密度激励,采用频域疲劳分析方法评估弹簧疲劳寿命。

首先,基于螺旋弹簧频响函数求解其应力响应PSD

S(f)=H2(f)F(f)

(6)

式中：S(f)为应力响应功率谱密度;H(f)为弹簧结构应力频响函数;F(f)为力功率谱密度。通过对弹簧有限元模型进行稳态动力学分析(即谐响应分析)得到,响应频率选至200 Hz。

在该模型中每个模态的节点频响函数的应力幅用作疲劳分析输入,基于应力功率谱密度曲线评估疲劳寿命并定位关键位置,采用Dirlik方法[21]中雨流幅值概率密度函数统计应力幅值-频次结合弹簧材料S-N曲线及Miner法则,基于疲劳损伤准则进行疲劳寿命计算

(7)

式中：N(S)为疲劳循环次数;vp为穿越因子;T为时间长度;p(S)为应力幅值为S的概率密度分布函数;m、C为材料S-N曲线参数。

该弹簧钢材料为60Si2CrVAT,S-N疲劳曲线定义了两点N=1×104,S=700 MPa,N=1×107,S=220 MPa,计算的螺旋弹簧组疲劳寿命云图,如图12所示。弹簧组的疲劳薄弱区域主要位于簧条内侧,其中内簧约1.2圈处附近寿命最短,为1.8×106次循环,该位置与弹簧模态应力最大位置及现场断裂位置一致。

图12 弹簧组疲劳寿命云图与断裂弹簧

为了更加清晰地比较簧条不同位置的疲劳寿命,提取内、外簧簧条内侧不同圈数的疲劳寿命结果,如图13所示。

由图13可见,两弹簧的疲劳寿命基本上呈现出沿弹簧中间位置的对称分布状态,其中间位置的疲劳寿命均为最高,向簧条两端延伸疲劳寿命显著下降,这与1.1节模态分析弹簧在中间位置的模态应力最小这一结果相对应。两者最高疲劳循环次数均接近于1012,而内簧最低疲劳循环次数为1.8×106,外簧最低为6.4×106,外簧最低寿命是内簧的3.6倍。这与1.1节模态分析弹簧在中间位置的模态应力最小这一结果相对应。并且内簧在上下两端1～2圈(即其1～2圈与8～7圈)之间为疲劳寿命最低的区域,这与该位置多阶模态应力为最大的结果也保持一致。

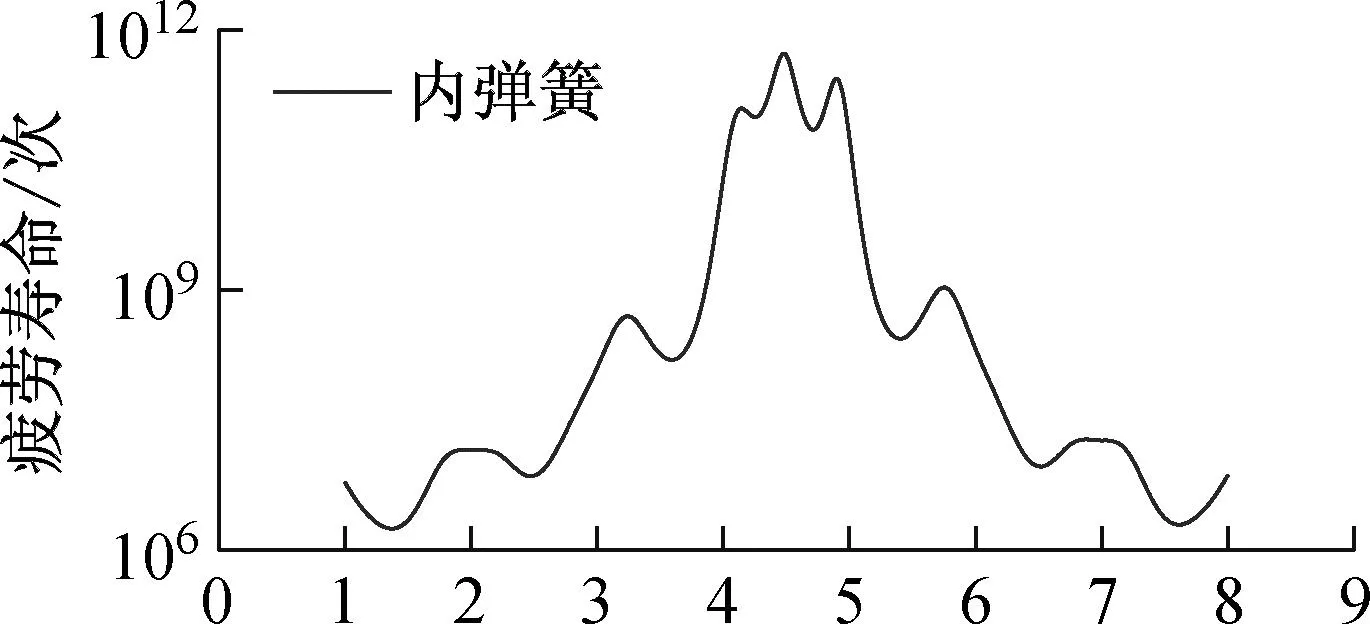
(a) 内簧

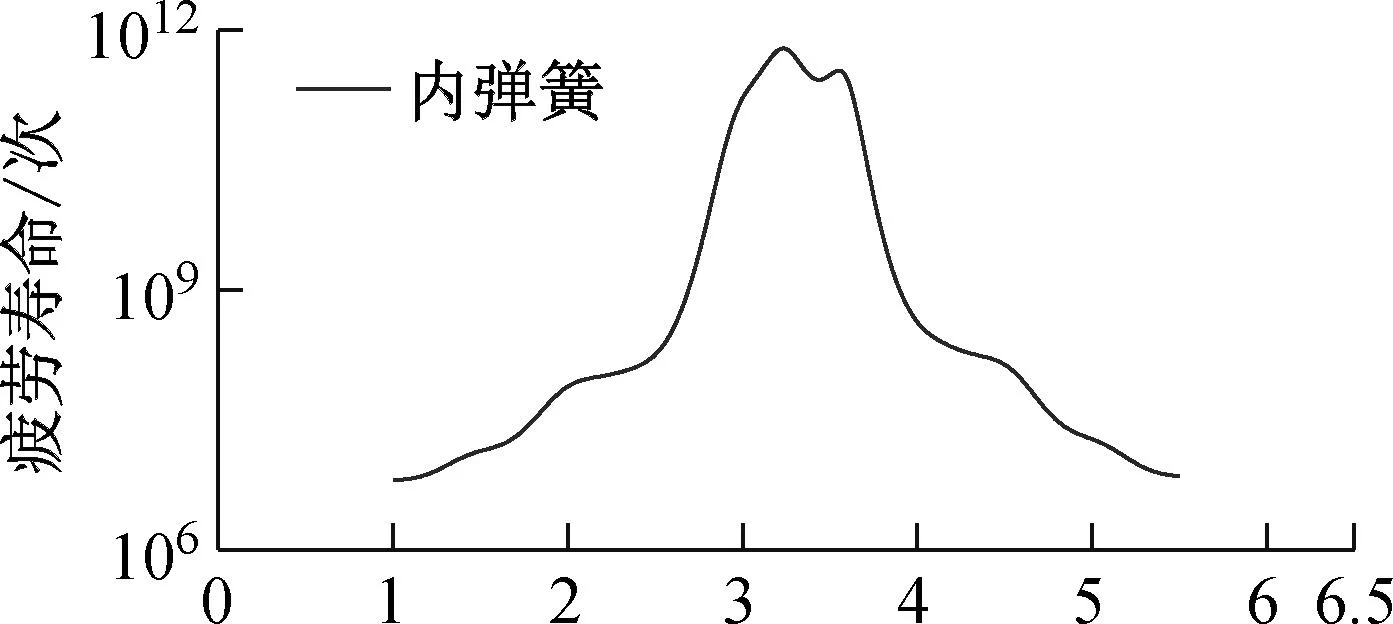
(b) 外簧

结合图11中内簧1.2圈内侧在58 Hz附近的动应力峰值结果,说明了本文研究的内簧在轮轨激励下产生了动态的振动疲劳失效,继而引发该位置的疲劳断裂。内外簧由于并联在一起,两端总体变形保持一致,但由于内簧一阶垂向模态频率58 Hz相对于外簧的一阶频率52 Hz,更加接近轮轨P2共振频率,使得其内部共振更为剧烈,外圈弹簧在其有效圈的端部疲劳寿命最低,但仍高于内簧的最低疲劳寿命数值。

4 结 论

本文针对轨道车辆一系悬挂螺旋弹簧簧条内侧断裂问题,建立包含螺旋弹簧动态特性的车辆 - 轨道耦合精细化动力学模型,求解服役状态由轮轨激励引起的结构两端动载荷,基于结构频域疲劳分析方法,计算簧条动应力与疲劳寿命,阐明一系螺旋弹簧振动疲劳失效机理。主要结论如下：

(1) 螺旋弹簧由于其自身动态特性,在各阶模态频率处,弹簧的振动峰值发生在簧条中间位置,而发生断裂的内簧1.2圈位置附近,其模态应力峰值为最大。

(2) 地铁普通扣件整体道床轨道结构的轮轨系统P2共振频率在60 Hz附近,与本文研究的车辆一系内簧前几阶固有频率接近,轮轨系统激励引起了内簧内部共振。

(3) 基于刚柔耦合动力学模型,计算服役状态下的内簧动应力响应与实测结果一致,在其一阶固有频率58 Hz附近簧条动应力响应为第二峰值的3倍以上,引起的疲劳损伤是其它频段的35倍。螺旋弹簧疲劳寿命计算结果显示,内簧1.2圈疲劳寿命最低为1.8×106疲劳循环次数,而外簧最短疲劳寿命约为内簧的3.6倍,解释了运行时一系内簧该位置频繁断裂的主要原因。

综上所述,本文所研究的一系内螺旋弹簧服役状态下由于轮轨激励引起簧条内部共振,其1.2圈位置在58 Hz附近出现较大的动应力响应峰值,继而引发疲劳损伤与振动疲劳失效。因而,一系弹簧自身模态频率应当远离该轮轨系统P2共振频率60 Hz区间,可减少内簧振动疲劳故障。本研究可为轨道车辆一系螺旋弹簧抗疲劳设计提供参考。