直观想象素养下的球体切接问题

雷 誉

(湖北省咸宁市青龙山高级中学)

空间几何体与球有关的切接问题,在立体几何中常常出现,是命题的热点和难点.本文就锥体的外接球与内切球问题进行探究和推广,帮助学生提升空间想象能力,提高学生的直观想象、逻辑推理和数学运算等核心素养.

1 例题探究

例1 已知四棱锥的各个顶点都在同一个球面上,若该球的体积为36π,则该四棱锥体积的最大值是_______.

方法2 利用基本不等式来求最值,即

当且仅当6－2h＝3＋h,即h＝1时,等号成立.

先将四棱锥的各个顶点放进一个圆锥中,当底面圆的内接四边形为正方形时,该四棱锥体积最大.据此可表示出四棱锥体积与球心到底面的距离h之间的函数关系,进而利用函数的单调性或基本不等式求得最大值.本题可以推广为结论1.

例2 球M是圆锥SO的内切球,若球M的半径为1,则圆锥SO体积的最小值为( ).

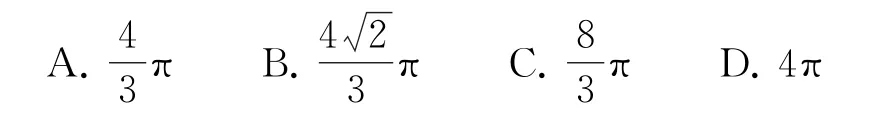
本题是圆锥的内切球问题,利用轴截面面积法或图形相似寻找等量关系,进而表示出圆锥体积,最后利用基本不等式或二次函数的性质求得最值.本题可以推广为结论2～结论4.

例3 现有10个直径为4的小球,全部放进棱长为a的正四面体盒子中,则a的最小值为( ).

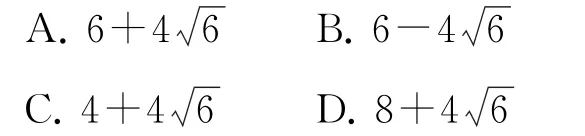
10个小球放进正四面体ABCD中,呈三棱锥形状,有3层,从上到下每层的小球个数依次为1,3,6.当a取得最小值时,每层放在边缘的小球

例4 图2 是某一零件的结构模型,中间的最大球为正四面体ABCD的内切球,中等球与最大球同正四面体三个面均相切,最小球与中等球同正四面体三个面均相切.已知正四面体ABCD的棱长为2 6,则模型中9个球的表面积之和为( ).

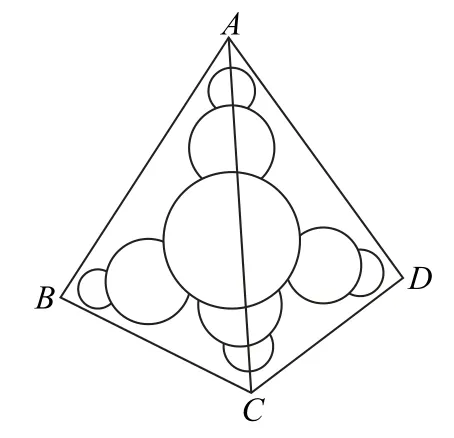
图2

如图3 所示,取BC的中点E,连接AE和DE,F为A在平面BCD上的投影点,则

图3

本题是正四面体和多个大小不等的小球相切问题,还可利用正四面体内切球的半径为棱长的的结论快速求出r＝1.多个大小不等的小球相切问题的处理方法是通过截面图的相似三角形,建立关系,得到这些球的半径之比为2,即最大球的半径是中等球半径的2倍,中等球的半径是最小球半径的2倍.本题可以推广为结论8.

2 结论推广

证明 可将四棱锥看成圆锥来分析,设圆锥的底面圆半径为r,高为h,其外接球的半径为R,则(h－R)2＋r2＝R2,得h2＋r2－2hR＝0,当四棱锥为正四棱锥时,其体积取得最大值

3 巩固练习

练习1 将一个半径为6的球削成一个体积最大的圆锥,则该圆锥的内切球的半径为( ).

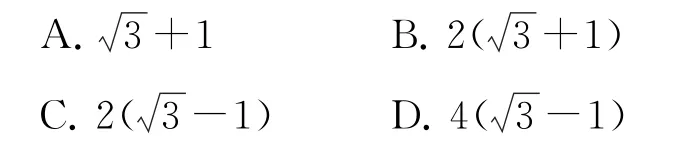
答案 D.

练习2 (多选题)如图4所示,有一个棱长为4 的正四面体P-ABC容器,D为PB的中点,E是CD上的动点,则下列说法正确的是( ).

图4

A.直线AE与PB所成的角为

B.△ABE的周长最小值为4＋ 34

C.如果在这个容器中放入1个小球(全部放入),则小球半径的最大值为

D.如果在这个容器中放入4个完全相同的小球(全部放入),则小球半径的最大值为

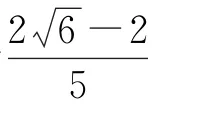
答案 ACD.

练习3 半正多面体亦称“阿基米德体”或“阿基米德多面体”,是以边数不全相同的正多边形为面的多面体,体现了数学的对称美.某半正多面体由4个正三角形和4个正六边形构成,其可由正四面体切割而成,如图5所示.已知MN＝3,若在该半正多面体内放一个球,则该球体积的最大值为( ).

图5

答案 A.

4 小结

求解立体几何中有关球的切接问题,有利于培养学生的直观想象、逻辑推理和数学运算等核心素养.数学问题的解决仅仅是一个开端,更重要的是解题后的反思与回顾.当遇到经典题目,不能仅仅停留在解题的层面,还应反思是否有其他解法,能否将试题进行拓展和推广,试题的本质是什么,这样才能将试题的价值最大化.

(完)