从结构寻解法 用思维提素养——一道解斜三角形统测题的解与思

王 凯 金建军

(1.浙江杭州市源清中学 2.浙江金华第一中学)

解三角形问题是高中数学的一类常见问题,它是初中数学解直角三角形问题的继承和发展,在解题时常结合高中的代数工具(如正弦定理、余弦定理、平面向量等),以解决复杂几何图形中的定量问题.本文以浙江省杭州市2022届高三下学期4月数学质量检测(二模)第16题为例简谈在解三角形问题时学生如何培养和落实自己的数学学科核心素养.

题目 在Rt△ABC中,∠C＝90°,点D在边BC上,3CD＝BD.若,求sin∠ABC.

本题的题干简洁,既有几何关系,又有数量关系.在画出草图后,可以从几何构造、代数运算和数形互助的层面来对问题进行解法建构,在解决问题的过程中提高解题能力,培养思维品质,提升核心素养.

分析1 题目没有直接给出图,所以解题时先要根据题意构图.题干中有一个条件:一个角的正弦值是,根据这个熟悉的值联想到“勾三股四弦五”的直角三角形.因此求解问题的关键在于能否看出数据背后的秘密.

解法1 根据题意,画出图1,因为三角形相似不改变角度大小,不妨设CD＝1,BD＝3(下同).过点D作DH⊥AB,交AB与点H,那么有

在 Rt △ADH中, 因 为,所 以AH＝4sin∠ABC,AD＝5sin∠ABC,则AB＝4sin∠ABC＋3cos∠ABC.因为Rt△BDH∽Rt△BAC,所以,即

化简可得

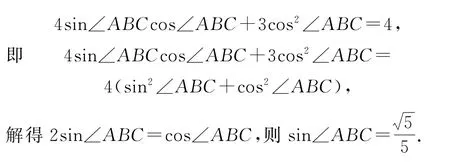
如果没有想到三角形相似,算“两次”也可以是我们解决此类问题的常用方法,如解法2.

解法2 在图1中,设DH＝3k,AH＝4k,AD＝5k,则在Rt△ABC中,有

又因为

所以

解法提炼 “能够在熟悉的数学情境中,借助图形的性质和变换(平移、对称、旋转)发现数学规律”是«普通高中数学课程标准(2017 年版2020 年修订)»(以下简称«课标»)对直观想象素养水平一的要求.欧几里得几何是学生在初中阶段的一个重要学习内容,通过一些常见的几何图形,建立直观想象思维,为后续用代数予以表达提供基础.学习时需要在基本图形中识别常见的图形,利用关联的情境,把问题变回到熟悉的数学情境中,然后利用合适的工具进行求解.

分析2 这个问题还可以借助高中数学中解三角形问题的两大工具——余弦定理和正弦定理,通过代数运算巧妙地替代添加几何辅助线.

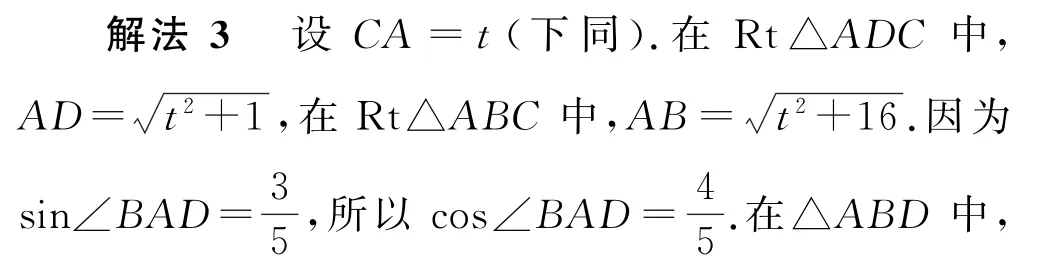
由余弦定理,得

即

解得t＝2,则

把边长用变量t进行表示,借助余弦定理这一代数工具,把几何运算转化成了代数运算.同理,也可以用正弦定理解决,如解法4.

解法4 在△ABD中,由正弦定理,得

即AD＝5sin∠ABC.在Rt△ADC中,得

故有

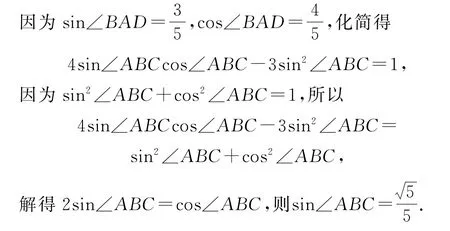
解法提炼 “能够在关联的情境中确定运算对象,提出运算问题”是«课标»对数学运算水平二的要求.事实上,在情境中理解运算是一种演绎推理,若能学会用程序化策略,将会有利于解决数学运算的问题.

分析3 在前面的解法中,利用了几何构图的“巧”和数学运算的“繁”,我们还可以从数形结合的角度,通过形看出一些关系,再用简单的运算得出结论,提升逻辑推理能力.

解法5 由题可知∠BAD＝∠BAC－∠DAC,因为∠BAC在Rt△ABC中,∠DAC在Rt△ADC中,所以这两个角的三角函数值非常容易算出,结合差角公式(在等号两边取正弦,直接用题中的正弦值;因为斜边结构比较复杂,可以在等号两边取正切值,这样计算更为简单),就能很快的建立等量关系,解得t＝2,则

如果采用这个解法,这个问题就可以看作是人教A 版必修第二册50页例10(如图2所示,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物高度AB的方法,并求出建筑物的高度)的一个改编题.教材中并没有把解三角形作为一个单独的章节,而是作为平面向量的应用,这也说明我们可以用向量的视角去审视问题,如解法6.

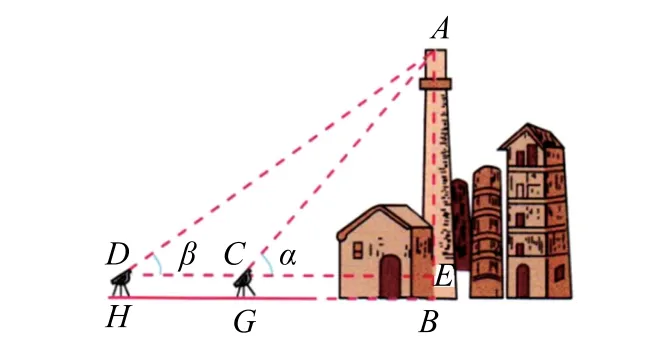
图2

图3

解得t＝2,则

解法提炼 “能够在综合的情境中,用数学的眼光找到合适的研究对象,提出有意义的数学问题”是«课标»对逻辑推理水平三的要求.从问题表征找到数量关系,培养从方法层面考虑问题,提升逻辑推理能力.

在日常解题中,既要重视通性通法,同时还要会从不同角度来思考问题,充分解读数学学科知识,挖掘数学知识背后的思维,不断提高自己的数学能力,以实现数学学科核心素养的提升.

(完)