初中数学几何最值问题的解题思路分析

刘桂景

【摘  要】  与几何图形有关的最值问题，既能考查学生对几何图形的掌握情况，也能探查学生的代数运算能力，具有十分重要的意义.求解几何最值问题主要从几何定理和代数运算两个角度切入，不同解题思路具有各自的特点.本文结合具体例题对不同解题思路做出分析，帮助学生多方面思考问题，提升综合能力.

【关键词】  初中数学；平面几何；最值；解题技巧

1  几何定理思路

运用几何定理解答几何最值问题，具体方法是灵活利用常见几何性质对几何图形中点、线、面进行等价转化，使最值问题等价转化为熟悉已知的图形，进而对问题作出解答.常见的几何定理或性质有两点之间线段距离最短、三角形两边之和大于第三边、两边之差小于第三边等，灵活运用这些几何定理，能解答大部分几何最值问题.

例1  如图1，直线与轴分别交于点，点在动点右侧的轴上，且始终满足，点在直线上，其横坐标为，请问：当为何值时，四边形的周长最小？最小值是多少？

剖析  四边形中的边长是定值，故最小值等价于求线段的最小值，通过构造平行四边形和对称点，结合两点之间线段最短定理，可明确最小值情况对应的图形，运用勾股定理列式运算，即可求出最小值以及四边形周长的最小值.

解析  ∵点在直线上，且横坐标为，

∴点，

，

∵是定值，

∴问题等价于求的最小值，

过点作关于轴的对称点，连接，如图6所示，

则是的最小值，

∵，，

∴，

∴四边形周长的最小值为：.

2  构造函数思路

构造函数思路是代数方面的解题思路，关键在于根据已知条件和关系构建函数解析式，将几何最值问题转化为函数求最值问题，进而对问题作出具体解答.常见的函数类型有：一次函数、一元二次函数以及反比例函数，找到几何问题中的等式关系并构造函数解析式，就能对最值问题作出解答.

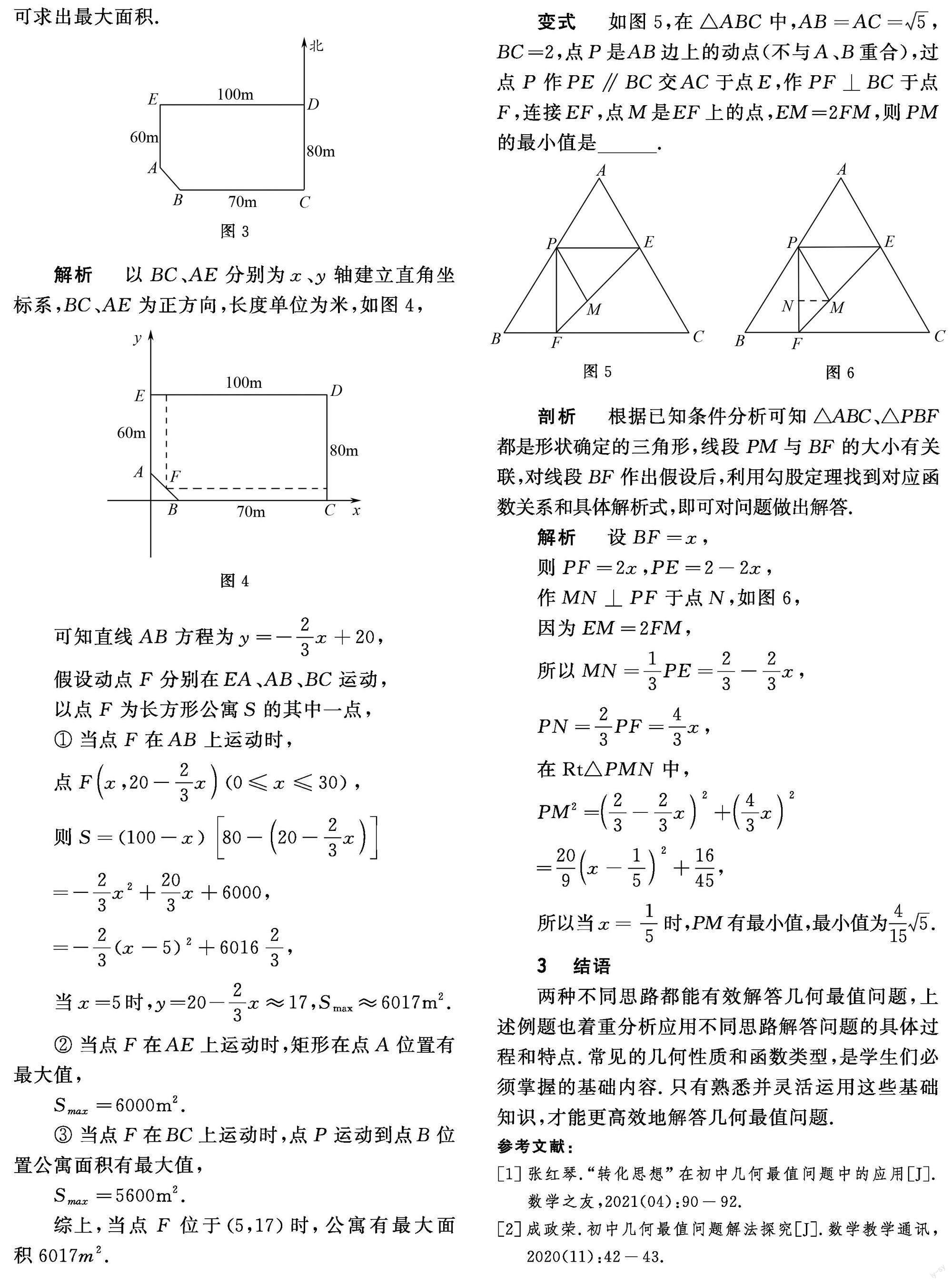
例2  某房地产公司拥有一块“缺角矩形”荒地，边长和方向如图3所示，要在这块地上建造一座长方形东西走向的公寓，请划出这块地基，并求出地基的最大面积（精确到）.

剖析 根据题意构造直角坐标系，在坐标系上将图形转变为对应函数，其次符合题意的面积需要分三种不同情况进行讨论，根据面积公式列出对应的函数解析式并判断对应最大值，综合分析比较即可求出最大面积.

解析  以分别为轴建立直角坐标系，

为正方向，长度单位为米，如图4，

可知直线方程为，

假设动点分别在运动，

以点为长方形公寓的其中一点，

①当点在上运动时，

点，

则，

，

当时，，.

②当点在上运动时，矩形在点位置有最大值，

.

③当点在上运动时，矩形在点位置有最大值，

.

综上，点位于时，公寓有最大面积.

变式  如图5，在中，，，点是边上的动点（不与重合），过点作交于点，作于点，连接，点是上的点，，则的最小值是______.

剖析  根据已知条件分析可知、都是形状确定的三角形，线段与的大小有关联，对线段作出假设后，利用勾股定理找到对应函数关系和具体解析式，即可对问题做出解答.

解析  设，

则，，

作于点，如图6，

∵，

∴，

，

在中，

，

∴當时，有最小值，最小值为.

3  结语

两种不同思路都能有效解答几何最值问题，上述例题也着重分析应用不同思路解答问题的具体过程和特点.常见的几何性质和函数类型，是学生们必须掌握的基础内容.只有熟悉并灵活运用这些基础知识，才能更高效地解答几何最值问题.

参考文献：

[1]张红琴.“转化思想”在初中几何最值问题中的应用[J].数学之友，2021（04）：90-92.

[2]成政荣.初中几何最值问题解法探究[J].数学教学通讯，2020（11）：42-43.