从一道习题来看从特殊到一般的思想

李映萱

【摘要】从特殊到一般的思想方法是学习研究数学的基本思想方法之一.本文对平面几何中一类三角形所具有的性质进行了探索，详细讲述了从特殊到一般，再从一般回到特殊的完整过程，对其中的关键问题的处理方法进行了合情的分析并用多种方法给出了严格证明.这种 结合实际问题的分析会对学生掌握从特殊到一般的思想方法有所裨益.

【关键词】思想方法；从特殊到一般；探索

1  引言

一个定理由条件和结论两部分组成，在证明定理时目标是明确的，任务是从条件出发调

动一切手段去证明结论.而提出一个问题常常是只有一些条件而没有结论，在经过一定的思考后会有一些发现，也许会有一些对于结论的猜想，这需要一个探索过程.在这种意义下提出问题比证明定理要困难一些[1]，[2].在探索发现过程中常常会从最简单的特殊情况出发，找到一些结论，然后逐步向较一般的情况扩展，直至有一个相对完美的结论，而这个结论可以用于符合条件的更多的具体问题.这就是从特殊到一般的方法.特殊问题的条件比较多，得到结论会容易一些，结论也会比较简单，从解决的过程中会得到一些有利于讨论一般情况的启发.问题的难处是在一般情况下怎样避开特殊情况下的附加条件，去发现去掉这些条件后结论会有什么变化.本文对一个探索性的问题实现一个完整的从特殊到一般，再到特殊（从具体到抽象再回到具体）的完整过程，希望对初学者有些启发.

2  问题的提出

已知在△ABC中，中线BF和CE互相垂直，请找出此三角形的边角的特殊关系.

3  特例探索

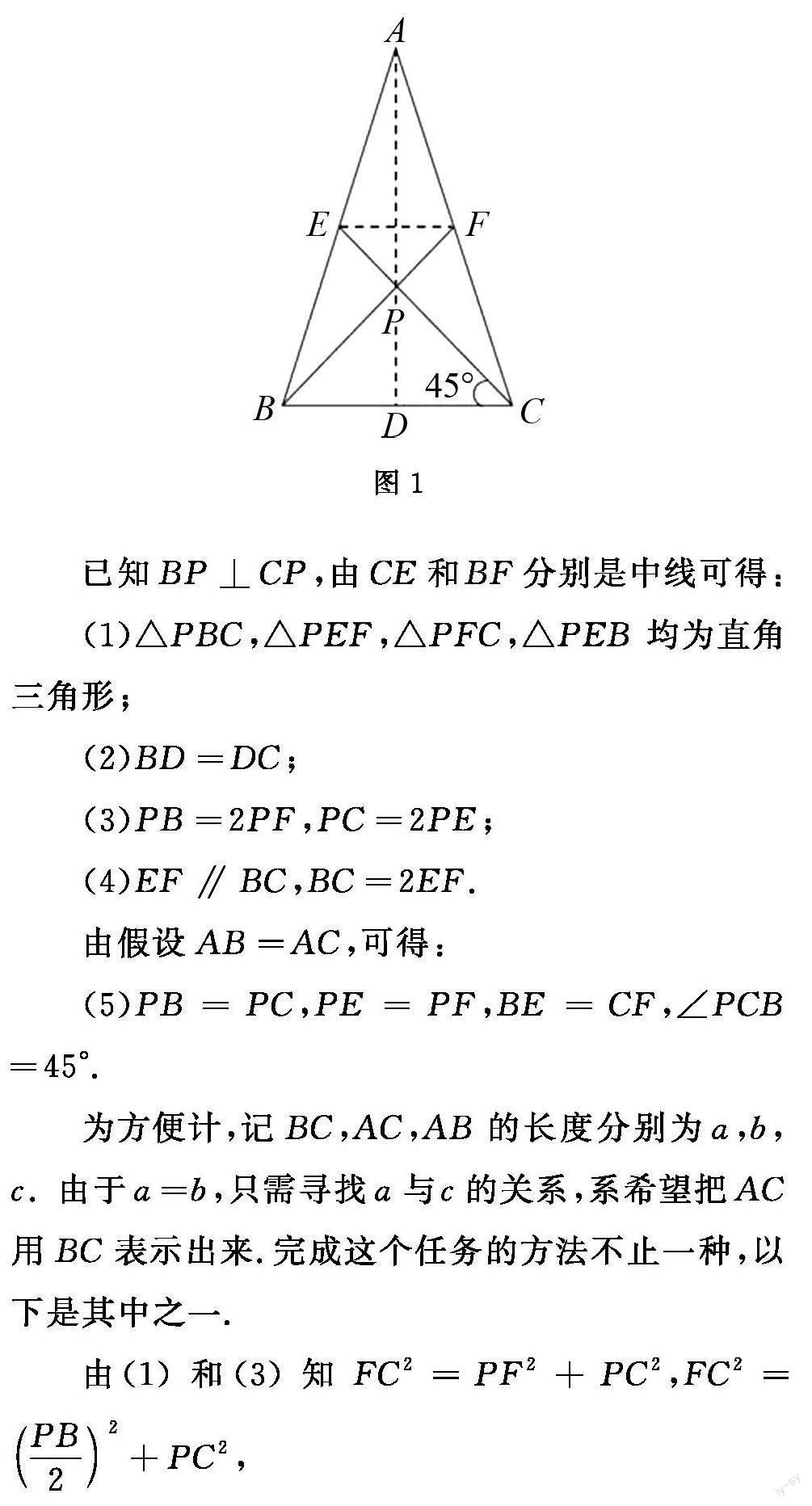
按照由特殊到一般的认识规律，可以从特殊的三角形出发探索三边边长的关系.由于等边三角形中线的夹角是120°，所以退而考虑等腰三角形.如图1所示，假设AB=AC，BF与CE相交于P.先列出已知和假设可以得到什么.

已知BP⊥CP，由CE和BF分别是中线可得：

（1）△PBC，△PEF，△PFC，△PEB 均为直角三角形;

（2）BD=DC;

（3）PB=2PF，PC=2PE;

（4）EF∥BC，BC=2EF.

由假设AB=AC，可得：

（5）PB=PC，PE=PF，BE=CF，∠PCB=45°.

为方便计，记BC，AC，AB的长度分别为a，b，c. 由于a=b，只需寻找a与c的关系，系希望把AC用BC表示出来.完成这个任务的方法不止一种，以下是其中之一.

由（1）和（3）知FC2=PF2+PC2，FC2=PB22+PC2，

PB2+PC2=BC2[3]，（6）

又由（5）知PB=PC=24b2=58a2，

b2=c2=52a2，（7）

此外由上式知a5，

从而cosC=1010.（8）

4  一般情况的探索

如图2，AB≠AC，（7）式和（8）式不再成立.要想得到一般情形下的结论，必须仔细分析前述推导中哪些受到了“等腰”的限制，哪些没有，然后进一步讨论怎样能去掉“等腰”的限制，得到一般情形下的结果.

复盘上面的推导，（6）式中的结果是从已知的（1）和（3）得到的，与“等腰”无关，对一般三角形仍成立，（7）式和（8）式的结果是由假设“等腰”得到的.等腰三角形是轴对称，一般三角形不具有这个特性，但是根据已知，二中线垂直决定了它有广义的对称，即点P的上下和左右各有一对直角三角形.（6）中的结果为

FC2=12PB2+PC2.（9）

（6）中的结果是由△PFC 得到的，与它对应的有△PEB，完全同样的操作，可以得到

EB2=12PC2+PB2 .（10）

二式相加利用（6）中的PB2+PC2=BC2即可消去PC，PB，得到：

FC2+EB2=12PB2+PC2+12PC2+PB2=45BC2，b2+c2=5a2.（11）

再由余弦定理[5] ，b2+c2=a2+2bccosA，

与（11）式比较得cosA=2a2bc.

从以上的分析可以得到如下的命题.

称两条中线互相垂直的三角形为“中垂三角形”，中垂三角形的中线相应的两边长的平方和等于第三边平方的5倍，第三边的对角的余弦等于第三边平方的两倍与两夹边乘积之商.

5  命题的证明

如图2， 已知在△ABC中，中线BF和CE互相垂直，记BC，AC，AB的长度分别为a，b，c.求证：b2+c2=5a2，cosA=2a2bc.

证法1  由已知 △PBC，△PFC， △PEB均为直角三角形，并且PB=2PF，PC=2PE，

分别在此三个三角形中应用勾股定理[4]有PB2+PC2=BC2；

FC2=PF2+PC2=12PB2+PC2；

FB2=PE2+PB2=12PC2+PB2  .

将后两式相加，并利用PB2+PC2=BC2得：

FC2+EB2=12PB2+PC2+12PC2+PB2=54BC2，

又AC=2FC，AB=2EB，故有b2+c2=5a2.

再由余弦定理，b2+c2=a2+2bccosA，

與前式比较得cosA=2a2bc.所证成立.

证法2   由已知，△PBC，△PEF，△PFC，△PEB 均为直角三角形，在这四个三角形里分别应用勾股定理，得到FC2=PF2+PC2；

EB2=PE2+PB2；

PB2+PC2=BC2；

EF2=PE2+PF2.

前两式相加得FC2+EB2=PF2+PC2+PE2+PB2=

PB2+PC2+PE2+PF2，

又BC=2EF，AC=2FC，AB=2EB，可得：

FC2+EB2=EF2+BC2

=54BC2，b2+c2=5a2 .

再由余弦定理，b2+c2=a2+2bccosA，

与前式比较得cosA=2a2bc.所证成立.

证法3  由已知，△PBC，△PEF，△PFC，△PEB 均为直角三角形，并且EF∥BC，BC=2EF.记∠PCB=α.

FC2=PF2+PC2=EFsinα2+BCcosα2，

EB2=PE2+PB2=EFcosα2+BCsinα2，

二式相加得：FC2+EB2=EF2+BC2=54BC2，b2+c2=5a2.

再由余弦定理，b2+c2=a2+2bccosA，

与前式比较得cosA=2a2bc.所证成立.

6  拓展应用举例

例题  如图3所示.在平行四边形ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD=25，AB=3，求AF的长.

分析  题目中的敏感词是“中点”和“垂直”，与上述证明的命题相联系，希望利用BE⊥EG构造一个“中垂三角形”，利用所得命题进行计算.

解  延长EG，使它与FC延长线交于Q，延长FE和QD使其交于P.

易知△EGD≌△QGC，CQ=ED=FC，C为FQ中点.

因为CD∥FP，所以DF=DQ，

又因为ED∥FC， 所以EP=EF，

即DF，EQ是△EGD的两条中线.

因为BE∥FD，所以BQ⊥FD，

于是△EGD是一个“中垂三角形”.

应用已经证明的命题知PF2+PQ2=5FQ2，

代入PE=2AB=6，FQ=AD=25，

得PQ2=64，PQ=8，AF=4.

7  结语

以上从一个习题出发实现了一个由特殊到一般，再由一般到特殊（或者说是从具体到抽象，再由抽象到具体）的完整过程.从特殊到一般是这个过程的难点，本文通过对这一习题的分析说明了解决这个难点的基本思想，应该分析解决特殊问题的过程中哪些可用于一般情况，哪些是受特殊条件约束的，保留可以用的，然后想办法避免这个约束，达到解决一般问题的目标.当然还需要多做一些这种类型的联系才能逐步掌握这个方法.本文受到骆传枢老师指导，在此深表感谢.

参考文献：

[1]华罗庚.数学归纳法＼.上海：上海教育出版社，1963.

[2]肖林元.如何高效学习数学＼.北京：机械工业出版社，2007.

[3]葛军.奥數教程＼.上海：华东师范大学出版社，2018.

[4]马复.数学（八年级上期）＼.北京：北京师范大学出版社，2006.

[5]人民教育出版社.普通高中课程标准实验教科书 数学（第二册）＼.北京：北京师范大学出版社，2006.