求数列通项公式的十种常见题型
田素伟
(上海市泥城中学,上海 201300)
数列是高考的必考内容,而数列的通项公式是数列的核心.如果题目中没有直接给出数列是等差数列或等比数列,如何把题目中的条件通过变形转化为等差数列或等比数列,进而正确地求出数列的通项公式?下面介绍几种常见的数列通项公式的求法.
1 直接利用等差(等比)数列的通项公式



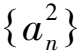






两边同时开平方,得


所以an=n2+2n-1.
2 用待定系数法求数列的通项公式
例2 数列{an}满足an=2an-1+3(n≥2)且a1=1,n∈N*,求数列{an}的通项公式.
解析由an=2an-1+3(n≥2),可设
an+x=2(an-1+x)(n≥2),
则an=2an-1+x(n≥2).
比较系数可得x=3.
所以an+3=2(an-1+3)(n≥2).
故{an+3}是以4为首项,2为公比的等比数列.
所以an+3=4×2n-1=2n+1.
所以an=2n+1-3.
点评形如an+1=Aan+B(A≠1且B≠0)或an+1=Aan+Bn(A≠1且B≠0),A,B均为常数的等式,常用待定系数法转化为等比数列再求通项公式.
变式已知数列{an}满足an+1=2an+3n且a1=1,n∈N*,求数列{an}的通项公式[1].





比较系数可得x=-1.



所以an=3n-2n.
3 构造特征函数
例3数列{an}满足an=4an-1+3(n∈N*,n≥2)且a1=0,求数列{an}的通项公式.
解析设f(x)=4x+3,令x=4x+3,解得x=-1.
由an=4an-1+3(n≥2),
an-(-1)=4an-1+3-(-1).
所以an+1=4(an-1+1).
所以{an+1}是以1为首项,4为公比的等比数列.
所以an+1=4n-1.
所以数列{an}的通项公式为an=4n-1-1.
变式数列{an}中,an是1和anan+1的等差中项,a1=2,n∈N*,求数列{an}的通项公式.
解析因为an是1和anan+1的等差中项,
所以2an=1+anan+1.








4 对于周期数列先求其周期




所以anan+2=-1.
所以an+4an+2=-1.
所以an+4=an.
所以数列{an}的周期为4.
因为a1=2,


5 递推关系式两边取对数
已知的递推关系式含幂指数或乘积的形式时,利用取对数方法进行变形转化为等差数列或等比数列,再求其通项公式.
例5 已知数列{an}满足a1=1,an+1=2nan,n∈N*,求数列{an}的通项公式.
解析因为an+1=2nan,a1=1,所以an>0.
两边同时取以2为底的对数,得
log2an+1=log22nan.
所以log2an+1=log2an+n.
设bn=log2an,则bn+1=log2an+1.
所以bn+1=bn+n.
所以bn+1-bn=n.
所以b2-b1=1,
b3-b2=2,
b4-b3=3,
…………
bn-bn-1=n-1.
以上各等式两边分别相加可得

又因为bn=log2an,


点评注意利用取对数的方法要满足an>0这一条件.另外本题还可以利用累乘法求解.
6 形如an=f(n)an-1+g(n)(n∈N*,n≥2)的数列
6.1 利用累加法
当f(n)=1时,形如an=an-1+g(n)(n≥2),n∈N*的形式,可利用累加法求数列的通项公式[2].
例6已知数列{an}满足a1=2,且an+1-an=2n+1,n∈N*,求数列{an}的通项公式.
解析因为an+1-an=2n+1,所以
以上各式两边分别相加
an-a1=2(1+2+3+4+…+n-1)+1×(n-1).
所以an=n2.
6.2 利用累乘法或者等式两边同时取对数的方法
当g(n)=0时,形如an=f(n)an-1(n≥2)的形式利用累乘法或者等式两边同时取对数的方法求数列的通项公式(见例10).

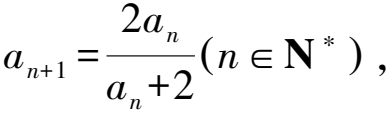





8 与正整数有关的和的等式求通项公式用分离法
例8 已知数列{an}的前n项和为Sn,且S1+2S2+3S3+…+nSn=n3,n∈N*,求数列{an}的通项公式.
解析由已知,n≥2时,
S1+2S2+3S3+…+(n-1)Sn-1+nSn=n3,
①
S1+2S2+3S3+…+(n-1)Sn-1=(n-1)3,
②
由①-②,得
nSn=n3-(n-1)3.

又当n=1时,S1=1也符合上式,

当n=1时,a1=1,


9 关于数列的奇数项和偶数项的通项公式
例9已知数列{an}满足a1=1,a2=2,an+2-an=(-1)n+2,n∈N*,求数列{an}的通项公式.
解析由已知条件an+2-an=(-1)n+2可知:当n为奇数时,an+2-an=1,{a2n-1}是以1为首项,1为公差的等差数列;
当n为偶数时,an+2-an=3,{a2n}是以2为首项,3为公差的等差数列.
所以当n=2k-1(k∈N*)时,
a2k-1=a1+(k-1)d=1+(k-1)×1=k.


当n=2k(k∈N*)时,
a2k=a2+(k-1)d=2+(k-1)3=3k-1.


所以所求数列的通项公式是
点评根据递推公式得出奇数项数列和偶数项数列各为等差数列,再结合已知数列的通项公式来求解问题,这里要注意奇数项和偶数项的首项.注意等式或不等式中出现(-1)n,一般都要分n为奇数和偶数进行讨论.
10 形如或a1=Aan+1-an=f(n)(A为常数,n∈N*)的数列求通项公式用累乘法或累加法
例10设数列{an}的前n项和为Sn,且a1=1,{Sn+nan}为常数列,求数列{an}的通项公式.
分析由已知可得出Sn+nan=2,进而可知Sn-1+(n-1)an-1=2(n≥2),两式两边分别相减得(n+1)an=(n-1)an-1,然后利用累乘法求出an即可.
解析因为{Sn+nan}为常数列且a1=1,
所以Sn+nan=S1+1×a1=2,
(1)当n=1时,因为S1+1·a1=2,所以a1=1.
(2)当n≥2时,由已知Sn+nan=2,
③
所以Sn-1+(n-1)an-1=2,
④
③-④,得(n+1)an=(n-1)an-1.


…………
以上等式两边分别相乘,得


点评本题考查利用an与Sn的关系求数列的通项,考查累乘法求通项,合理递推作差是解答的关键.本题注意要写出前四个等式和最后两个等式,可以方便观察,本题着重考查推理与运算能力.

