一道2023年浙江省预赛试题的解法探究
栾 功
(南宁市第三中学,广西 南宁 530021)
1 试题呈现

1)求椭圆的方程;
2)联结AP交椭圆于点C,过点C作x轴的垂线,交椭圆于另一点D,求S△ABD的取值范围.
(2023年全国高中数学联赛浙江赛区预赛试题第13题)
分析试题从椭圆的上顶点构图设计,通过创设一个纯几何的背景求解S△ABD的取值范围,考查学生先用几何的眼光观察分析问题,再通过代数运算解决问题的能力.灵活多样的构图设参给不同学生发挥各自能力水平提供了空间,试题达到通过加大思维强度来选拔拔尖创新人才的目的.
2 解法探究
解法1如图1,记C(x1,y1),则D(x1,-y1),直线AP,AB的方程分别为

图1

(25+t2)x2-50tx=0,

从而
故点D到直线AB的距离为
当t∈[-4,-1]时,
|t2+5t|=-(t2+5t),


评注解法1是解决这类问题的通用方法.该解法从|AB|为定值入手分析问题,将S△ABD的取值范围问题转化为点D到直线AB的距离d的范围问题.但在具体的解答过程中,不论是点D的坐标的求解,还是面积函数最值问题的解答,都对学生解决问题的基本能力和基本经验有较高的要求.
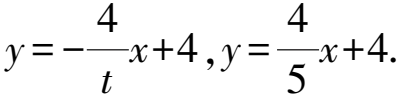



椭圆Γ在第二象限的方程为


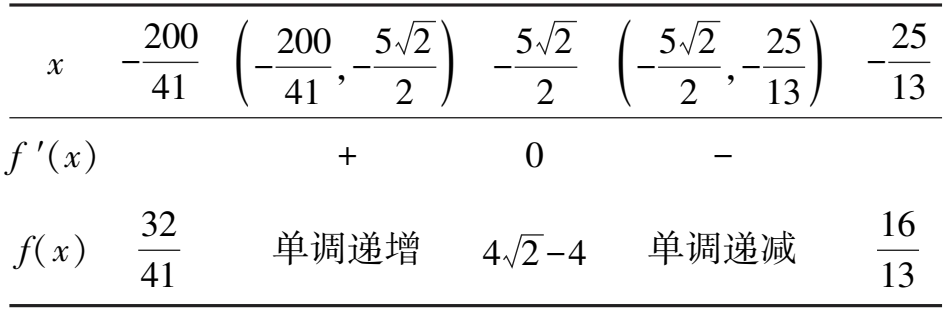
表1 x,f ′(x),f(x)的变化情况

此时
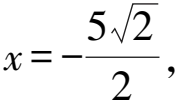
此时


解法3设直线AP的方程为
y=kx+4,

S△ABD=S△BOD+S△AOD-S△AOB

令5k-4=u,则u∈[1,16],得
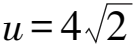
当u=16时,
故
评注解答解析几何问题要坚持“多想少算”的优化意识,而对图形特征的深入分析往往能使问题柳暗花明.该解法通过对形的深入分析,巧妙地将所求三角形的面积转化为点D横纵坐标的相关计算,在很大程度上优化了运算.当然,数形结合只是优化运算的一种途径,在这里还可以借助三角形面积的行列式公式、矢量积公式等快速建立三角形的面积与对应点坐标间的函数关系.
解法4设直线AD的斜率为k,则直线AD的方程为y=kx+4.记直线AD与x轴交于点Q,则
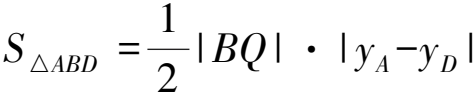

即

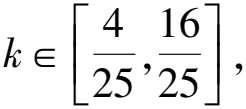


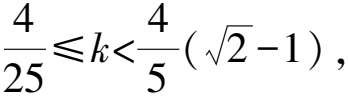


故
评注从不同的视角看待一个数学问题,会凸显出其不同的侧面.在问题本质的难度一定的情况下,选择不同的视角虽未改变问题的本质难度,但有利于揭示问题的内在规律,这对于培养学生分析问题和解决问题的能力大有裨益.
3 变式探究
思考1在上述解答过程中我们发现,△ABD面积的范围问题其本质是点D在椭圆Γ上运动变化时铅垂高|DE|的取值范围问题.结合解法1和解法2的运算过程和逻辑推理,对于问题揭示的本质有如下更一般性的推广.



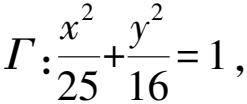

(25+16m2)y2+32mty+16(t2-25)=0,
从而
由点B,A′,Q共线知
整理,得
于是
故


推广3和推论4的证明同变式1的解答,此处不再赘述,目前抛物线还未发现类似性质.
思考3随着解题过程的不断深入,试题蕴含的本质得以逐步揭示,但试题所体现的价值往往不止于此.通过进一步分析几何特征、变换问题、更新试题结构等途径提出更具原创性的问题,以获得更高层次的思维历练,形成更深刻的理解和感悟.

证明设直线BC的方程为
y=kx-4.
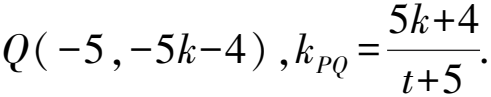
(16+25k2)x2-200kx=0.
由xB=0,得
因为点A,P,C共线,所以
代入y1=kx1-4,化简得

故

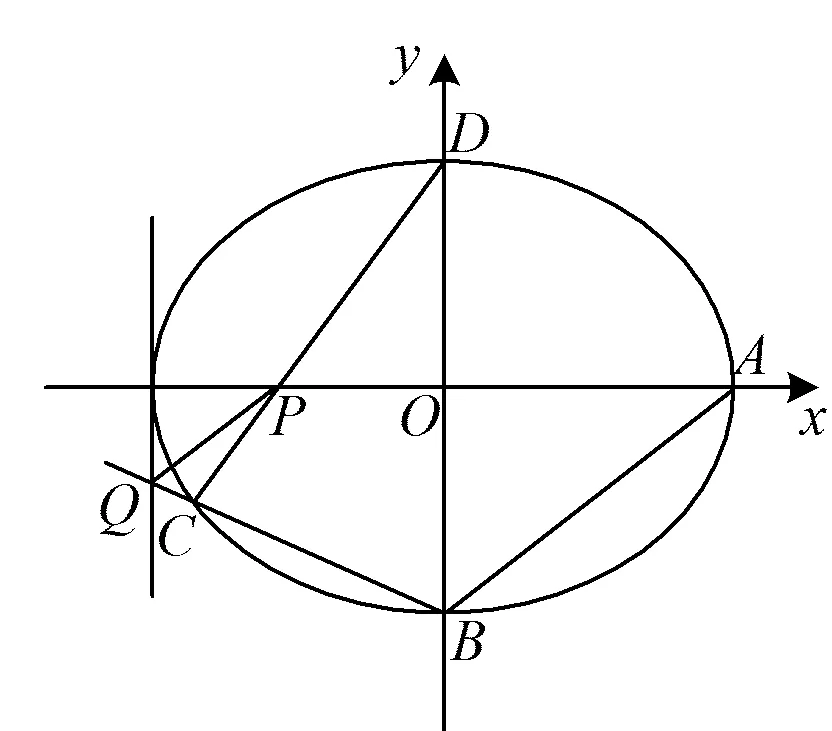
图2

1)四边形ABCD的面积是否为定值;
2)S△PCD是否有最大值.

E′:x′2+y′2=16.

令y′=0,得
则直线P′B′的方程为
令x′=0,得
于是

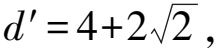

图3
由于S△P′C′D′=S△P′A′B′-S△A′B′C′D′,因此
故S△PCD有最大值,且
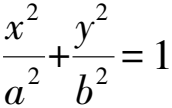
1)S四边形ABCD=ab;

4 结束语
2023年5月29日下午,习近平总书记在主持中共中央政治局就建设教育强国进行第五次集体学习时强调,基础教育既要夯实学生的知识基础,也要激发学生崇尚科学、探索未知的兴趣,培养其探索性、创新性思维品质.而每年的全国高中数学联赛试题往往具有丰富的内涵,正如例1,融解析几何基础知识、基本方法、闭区间上函数的最值问题于一体,深入考查学生的知识基础,同时试题从椭圆的上顶点构图设计,又极具探索性,是培育学生创新思维和数学思维很好的素材.因此,对各省市预赛试题价值的挖掘值得引起一线教学的重视.

