任意线性荷载下悬臂梁半逆解法研究

易 超

(西南交通大学土木工程学院,四川成都 610031)

0 引言

悬臂梁在土木工程中有着广泛应用,如房屋结构中的挑梁,基坑围护结构中的挡土桩,边坡加固中的抗滑桩等均可看做悬臂梁[1]。材料力学基于平衡方程、物理方程和平面假定给出了常见短梁的计算结果[2],但由于把梁假设为纵向纤维受拉的杆件,无法得到其内部应力分布和变形情况,忽略了挤压应力的存在。弹性力学[3-4]给出了在集中荷载和均布荷载作用下悬臂梁的弹性力学解;南忠俊[5]、张琦跃[6]分别给出了矩形截面梁在受到纯二次和四次分布荷载时的应力函数和应力解,但其求解模型中荷载在梁上最小值为0,在实际应用中往往很少出现这种情况,更多情况是呈梯形分布的荷载;刘鸿[7]计算基坑中双排抗滑桩位移时将其看做立起来的悬臂梁,采用弹性力学应力函数法分别求出矩形分布荷载和三角形分布荷载对桩产生的位移后再叠加的计算方法,计算过程较为繁琐。而针对悬臂梁在任意线性荷载作用下的该如何采用弹性力学半逆解法求解,尚无学者提出。

1 理论推导

1.1 确定应力函数

采用弹性力学半逆解法求解受荷变形问题,关键在于如何选取既满足相容方程又满足边界条件的应力函数[8]。随着受荷形式的愈趋复杂,应力函数的选取也愈困难,对受多项式分布荷载的狭长截面梁通常取应力函数为多项式形式[9]。

设有模型如下(为便于计算,按平面应变问题考虑且不计体力):

图1 推导模型

梁长为d,梁高为h,上边缘受到大小为q(x)=q+kx的分布力作用,根据材料力学理论很容易得到横截面上的正应力为式(1)。

(1)

式中:M(x)为弯矩;Iz为横截面惯性矩;

对于给定的梁Iz为常数,因此将上式看成一个与x有关的函数和与y的函数的乘积。在弹性力学中有式(2)。

(2)

积分之后得到的应力函数应为数项关于x和y的函数乘积之和,形如式(3)。

(3)

式中:n为分布荷载的次数。

因此本文可选取应力函数为式(4)。

φ(x,y)=x3f3(y)+x2f2(y)+xf1(y)+f0(y)

(4)

式中:f3(y)、f2(y)、f1(y)、f0(y)为关于y的待定函数,应力函数应当满足相容方程

并且x在区间[0,d]上满足,所以与x有关项系数应等于零,可求得各待定函数为式(5)～式(8)。

f3(y)=Ay3+By2+Cy+D

(5)

f2(y)=Ey3+Fy2+Gy+H

(6)

(7)

(8)

将式(5)～式(8)代入式(4)得应力函数为式(9)。

φ(x,y)=x3(Ay3+By2+Cy+D)+

(9)

1.2 应力求解

根据应力函数与各应力分量之间的关系,得到各应力分量为式(10)～式(12)。

(6Ax3+6Ex2+Jx+M)y+2Bx3+2Fx2+Kx+N

(10)

2(Ey3+Fy2+Gy+H)

(11)

(12)

式(10)～式(12)中A～L为待定系数,可根据应力边界条件确定。

主要边界条件为:

当x=0时,梁左端为次要边界,力的分布形式未知,可用圣维南原理放松

主要边界条件应当精确满足,即x的各次项系数为0,根据上述边界条件可建立13个方程,应力函数中共有13个待定系数,将所有方程联立可解得所有待定系数如下:

对于右端固定端边界,根据弹性理论,对于一个平衡体,如果物体内部满足平衡微分方程,在精确满足主要边界条件,以保证解的有效性的前提下,仅需满足部分力的边界条件时,剩余部分边界条件在积分意义下可自动满足,因此可无需验证。

将所求得的待定系数的值代入式得到各应力分量如式(13)～式(15)。

(13)

(14)

(15)

1.3 位移求解

根据弹性力学物理方程和几何方程可得到水平位移、竖向位移的计算式和剪应力的相等关系为式(16)～式(18)。

(16)

(17)

(18)

式(16)～式(18)中:E为弹性模量;μ为泊松比;u、v分别为x、y方向的位移见式(19)、式(20)。

所以

(19)

(20)

将式代入式得到式(21)。

(21)

将式左右两边分别看成是关于x、y的函数,并令其左右两边相等等于一个常数ω,则得式(22)、式(23)。

(22)

(23)

对式积分得到式(24)、式(25)。

(24)

(25)

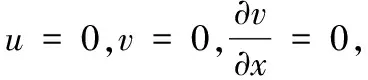
因此悬臂梁内任意一点的位移为式(26)、式(27)。

(26)

(27)

令y=0,可得到挠度方程为式(28)。

(28)

2 结果讨论

在本推导模型中,由于按照平面应变问题考虑,截面宽度取为一个单位宽度,根据材料力学理论, 梁的弯矩和剪力分别为

悬臂梁在受任意线性荷载分布荷载下材料力学应力解为式(29)。

(29)

若规定挠度向下为正,可得到材料力学中的挠度方程为式(30)。

(30)

对比式可知,材料力学解的σx、τxy分别为对应弹性力学应力解得第一项,弹性力学中其余项为修正项;σy为挤压应力,与材料力学结果完全不一致,这是因为在材料力学中作了纵向纤维受拉的假定,忽略了挤压应力的存在,因此,这也在预料之中[10-11]。

对比式可知,对于挠度方程,材料力学的解答均能在弹性力学应力函数解答中找到与之对应的项,材料力学中对挠度计算采用了简化处理的方法且没有考虑到泊松比对变形的影响,弹性力学解将泊松比考虑进去,对结果行了修正,式剩余的四项正为弹性力学的修正项。相比于材料力学解答结果,弹性力学解答不仅能得到挠度方程,也能得到物体内部任意一点的应力与变形,这在解决与其他物体接触时的变形协调问题时相比于材料力学更具有优势。

此外,在式中若分别令k=0和q=0可得到悬臂梁分别在均布荷载和三角形荷载下的各应力和位移解,相较于仅受均布荷载或三角形荷载下悬臂梁的弹性力学解,本文推导结果适用性更广,如在工程中遇到悬臂梁受梯形分布、三角形分布或均布荷载的情况时无需重新推导,可直接适用。

3 算例

某悬臂梁长5 m,横截面高0.8 m,弹性模量为E=210 MPa,泊松比μ=0.2,在梁上受到q(x)=(6+2x) kN/m的分布力作用,为简化计算在此不考虑重力作用。

根据本文所得结果与材料力学所得结果计算出挠度方程w、切应力τxy、固定端的正应力σx以及自由端挤压应力σy方程,并与ABAQUS有限元结果进行对比分析如表1、图2～图6所示。

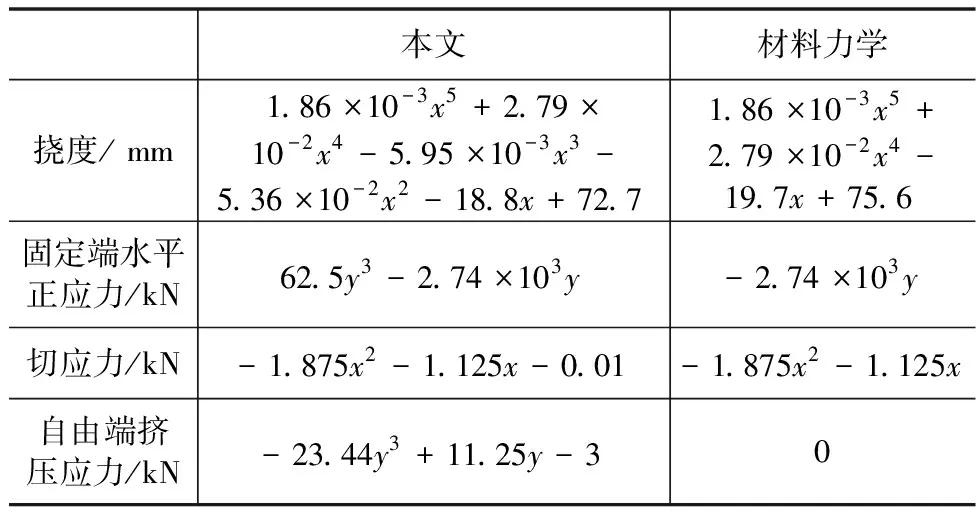
表1 各方程对比

图2 位移云图

图3 挠度变化

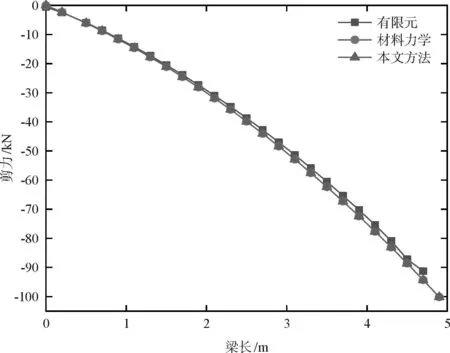
图4 中性轴线剪力

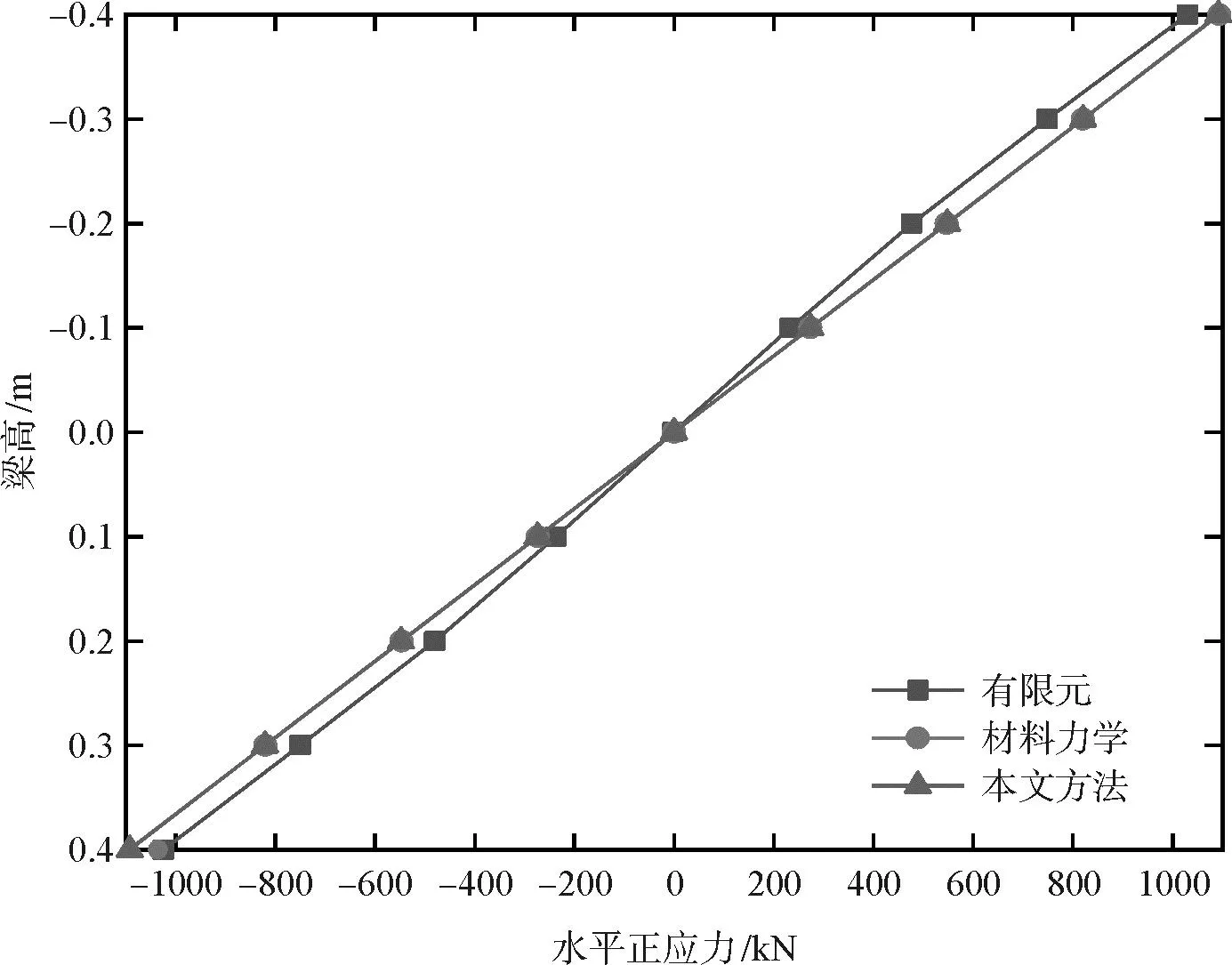
图5 固定端水平正应力与梁高变化

图6 自由端挤压应力

将理论结果与有限元结果绘制在同一图中梁的挠度,材料力学计算结果最大,有限元结果居中,应用本文方法计算结果最小,但三者在自由端最大误差在3 mm以内,满足要求;对于梁中性轴上的剪力,与材料力学结果基本一致,仅相差一个0.01 kN的修正项,有限元计算结果最小,三者误差在1%以内,满足工程设计要求;对于固定端的正应力,材料力学结果最大,有限元计算结果最小、应力函数法计算结果居中,与材料力学结果相比多了一项62.5y3,但相对误差很小,两者沿梁高方向正应力曲线基本完全重合;对于挤压应力,材料力学中将其忽略为零,这显然与实际情况不符,本文方法计算出挤压应力沿梁高呈三次曲线分布,中性轴以上较有限元结果稍偏大,中性轴以下较有限元结果稍偏小,整体分布规律一致。

4 结论

(1)针对悬臂梁在工程中应用广泛,材料力学解答无法得到其内部任意一点的应力和变形,从材料力学理论与弹性力学受力边界条件进行分析,提出了任意线性荷载下悬臂梁的应力函数表达式。

(2)根据边界条件对未知量进行求解得到了相应的应力和位移表达式并与材料力学结果进行了对比分析,表明材料力学中的挠度、正应力、切应力在本文推导的结果中都能找到与之对应项,本文结果在材料力学结果之上多出了修正项。

(3)材料力学结果没有考虑挤压应力,本文方法求得挤压应力沿梁横截面高度呈三次曲线分布,大小与数值模拟结果基本一致。

(4)选取一个实际案例分别应用材料力学结论、有限元和本文推导结果分别计算出挠度、剪力、固定端正应力和自由端挤压应力分布形式,并将3种方法所得结果进行对比分析,进一步验证了本文所提应力函数和求解结果的优越性和可行性。