基于犹豫模糊集的凝聚式层次聚类算法

李文全，毛伊敏，彭新东

基于犹豫模糊集的凝聚式层次聚类算法

李文全*，毛伊敏，彭新东

（韶关学院 信息工程学院，广东 韶关 512005）（∗通信作者电子邮箱78192128@qq.com）

针对犹豫模糊聚类分析存在信息失真、属性权重客观性差、时间复杂度高的问题，提出一种基于犹豫模糊集的凝聚式层次聚类算法（AHCHF）。首先，采用犹豫模糊元的平均值扩充犹豫度小的数据对象；其次，利用原始信息熵和内部最大差异计算数据对象扩充前后的权重，并根据两个权重向量之间的最小鉴别信息确定属性的综合权重；最后，以加权距离和更小为目标，给出犹豫度恒定的中心点构造方法。在具体实例和人造数据集上进行的实验结果表明，相较于经典的犹豫模糊层次聚类算法（HFHC）和较新的模糊层次聚类算法（FHCA），AHCHF的轮廓系数（SC）均值分别提高了23.99%和9.28%，运行时间分别平均减少了27.18%和6.40%。以上结果验证了所提算法可以有效解决信息失真、属性权重客观性差的问题，并较好地提升聚类效果和聚类性能。

犹豫模糊集；聚类分析；犹豫度；数据挖掘；模糊熵

0 引言

聚类分析［1］按照一定规则将数据对象集划分为若干个不同类簇，使同一类簇的数据对象间的相似性尽量大、不同类簇对象间的相似性尽量小，以挖掘隐藏在其中有价值的信息和知识。典型的聚类算法有基于划分的均值聚类算法［2］、基于层次的变色龙算法［3］、基于网格的空间聚类算法［4］和基于密度的噪声应用空间聚类算法［5］等，这些算法被广泛应用于管理和医疗等领域。

Chen等［19］依据Pearson系数原理定义了犹豫模糊集的相关系数，并利用等价矩阵和传递闭包，提出了犹豫模糊集的层次聚类算法；Zhang等［20］提出了基于最小加权汉明距离的犹豫模糊凝聚层次聚类算法；王志飞等［21］设计了数据集的权重公式和构造了簇中心的计算公式，提出了一种凝聚中心犹豫度恒定的模糊聚类算法，但它的权重没有考虑犹豫度扩充后信息量的变化；张煜等［22］给出了犹豫模糊元素集的补齐方法和距离函数权重计算公式，利用密度峰值选取簇中心，提出了基于密度峰值的加权犹豫模糊聚类算法；孙爽爽等［23］设计了可扩展的犹豫模糊集的加权相似度计算公式，提出了犹豫模糊数据对象集的谱聚类算法；邓小燕［24］运用核函数将数据映射到高维特征空间，保证原始样本结构不变的情况下扩大样本间的差异性，提出了犹豫模糊核C-均值聚类算法。

尽管上述算法都取得了较好的聚类效果，也在多个领域得到了应用，但仍存在多方面不足，主要体现在如下几点：

1）犹豫度扩充导致信息失真。在犹豫模糊元运算时，需要取最大元或最小元扩充犹豫度小的数据对象，扩充后会使原有信息量发生改变，导致信息失真。

2）人为主观给定属性权重。既没有考虑犹豫度扩充前的原始信息，也没有考虑扩充后对犹豫度和模糊性的影响，属性权重的客观性较差。

3）新类中心点的构造性能不理想。采用平均算子构造中心点，时间复杂度高且空间复杂度呈指数级增长，严重影响算法性能。

为解决上述问题，本文提出一种基于犹豫模糊集的凝聚式层次聚类算法（Agglomerative Hierarchical Clustering algorithm based on Hesitant Fuzzy set， AHCHF）。

本文的主要工作如下：

1）提出保持信息熵不发生改变的犹豫度扩充方法。采用犹豫模糊元的平均值扩充犹豫度小的数据对象，避免犹豫度扩充导致信息失真。

2）提出基于最小鉴别信息的综合权重计算方法，利用原始信息熵和内部最大差异计算犹豫度扩充前后的权重，并根据权重向量之间的最小鉴别信息确定综合权重，以解决人为主观权重存在客观性差的问题。

3）提出犹豫度恒定的中心点构造方法。在保持犹豫度不增加的情况下，利用平均算子计算中心点的最小元和最大元，并根据分箱原则，确定中心点的其他元素，以此构造加权距离之和更小的中心点，解决以往算法存在时间复杂度高、空间复杂度呈指数级增长的问题。

最后，在具体实例和人造数据上验证了所提算法的有效性。实验结果表明，与经典的犹豫模糊层次聚类算法（Hesitant Fuzzy Hierarchical Clustering algorithm， HFHC）［17］和最新的模糊层次聚类算法（Fuzzy Hierarchical Clustering Algorithm， FHCA）［21］相比，AHCHF在有效解决信息失真、属性权重客观性差问题的基础上，提升了聚类效果，减少了聚类时间。

1 相关工作

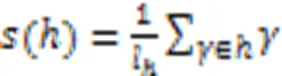
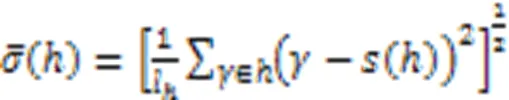
2 AHCHF

2.1　算法思想

AHCHF首先对数据预处理，通过扩充犹豫度，使同一属性下的特征值具有相同犹豫度；其次，把每个数据对象看成一个类，计算类间的加权距离，找出最小距离并合并成新的类；最后构造新类的中心点和计算新类与其他类之间的加权距离，不断合并最小距离的类，直到所有的数据对象聚成一类。根据算法思路可知，它主要包含犹豫度的扩充、属性权重的确定和聚类中心点的构造这3个阶段。各阶段的主要任务有：1）犹豫度的扩充。针对犹豫度不相等的情况，采用犹豫模糊元平均值填充的方法，扩充犹豫度小的数据对象，解决犹豫度扩充导致信息失真的问题。2）属性权重的确定。利用信息熵确定犹豫模糊元扩充前的原始权重，利用犹豫模糊元的最大离差确定扩充后的权重，并根据两者之间的最小鉴别信息确定综合权重，解决人为主观给定属性权重问题。3）聚类中心的构造。以加权距离和更小为目标，在犹豫度不增加的情况下，构造新类的中心点，解决算法性能较低下的问题。

2.2　犹豫度的扩充

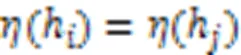
另外，根据得分函数与平均值的定义可知，它们的值都是犹豫模糊元的平均值，故有：

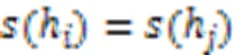
综上，由于得分函数与离差度都没有发生改变，则有：

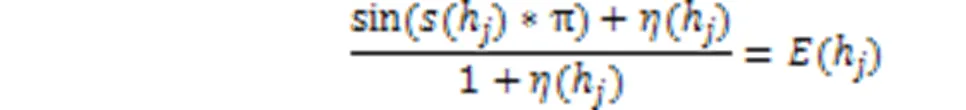
依据定理1，犹豫度扩充的主要步骤如下：

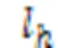
算法1 犹豫度扩充算法。

1） 初始化数据：

for=1 todo

找出当前属性下的最大犹豫度

end for

2） 元素排序：

repeat

for=todo

分别找出最大值和最小值下标

end for

将最大值放在最后，最小值放在最前

until（<）

for=1 todo

大于平均值的元素向后移动

end for

2.3　属性权重的确定

属性权重在聚类分析中起着举足轻重的作用，权重的微小变化都可能产生不同的聚类结果。以往的属性权重是人为设定的，主观因素影响大，没有考虑数据扩充前后信息量的变化，客观性和科学性不足。本文提出基于最小鉴别信息的综合权重的方法，它先使用熵权法确定犹豫模糊元素扩充前的原始权重，其次用最大离差法确定犹豫度扩充后的权重，再次利用最小鉴别信息构造犹豫模糊元素的综合权重，以此解决人为主观给定属性权重问题。该方法需要分别计算数据对象的原始权重、扩充后权重和综合权重。

1）原始权重。

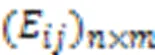
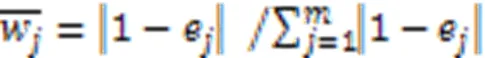
2）扩充后权重。

扩充后权重是利用最大离差法计算数据对象扩充后的属性权重。最大离差法利用犹豫模糊元的边界和内部之间的差异计算属性权重的方法。犹豫模糊元素的差异越大，说明属性对聚类结果影响较大，应该赋予较大的权重；犹豫元素差异越小，说明属性对聚类结果影响较小，应该赋予较小的权重。由此可知，属性权重的选择应该尽可能地使属性对所有对象的总偏差最大。根据此原则，构造犹豫模糊环境中属性权重的计算模型［26］，具体为：

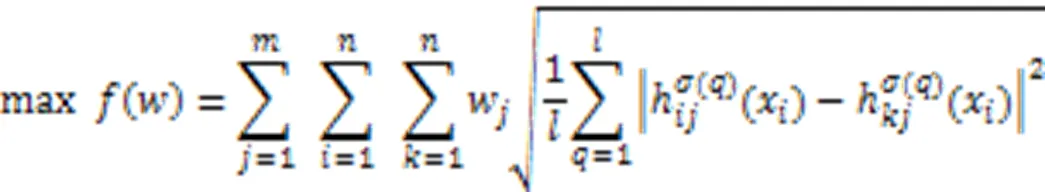
构建式（7）的拉格朗日函数，并求解得到：

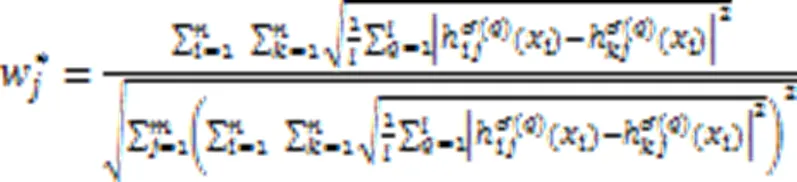
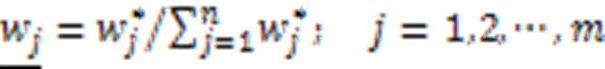
3）综合权重。

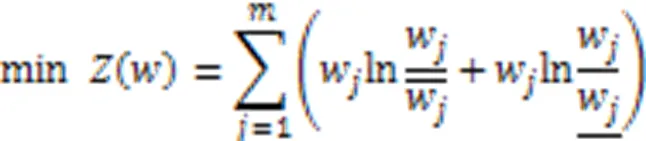
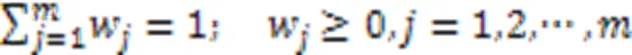
求解式（10），得到第个属性的综合权重：

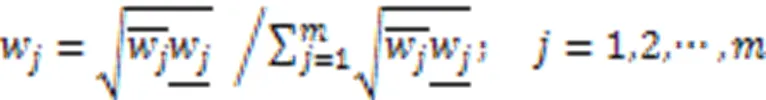
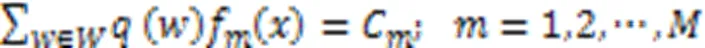
则最小权重鉴别信息分布满足

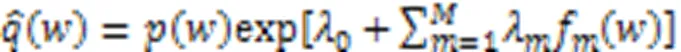
证明 取先验权重分布与目标权重分布之间的鉴别信息为目标函数，以最小鉴别信息为准则，则：

则有：

通过定理2可知，利用最小鉴别信息构造的综合权重，既能较好地反映扩充前的信息量，又能客观地反映扩充后对信息量的影响。具体实现过程如算法2所示。

算法2 确定综合权重算法。

for=1 todo

根据式（5）计算犹豫模糊熵

end for

for=1 todo

end for

for=1 todo

end for

2.4　聚类中心的构造

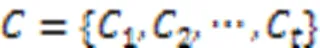
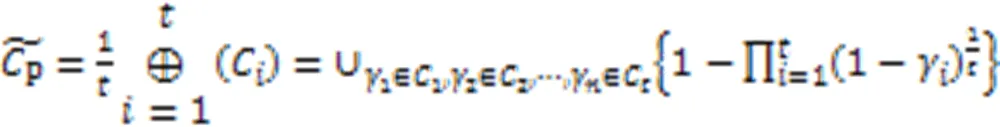
根据平均算子原理，由多个数据对象形成簇心时，中心点的计算需要取遍所有集合的所有元素，是集合元素的全排列。中心点的犹豫度是所有集合犹豫度的乘积。随着聚合对象的增多，计算簇心的时间复杂度将迅速增加，同时空间复杂度呈指数级增长，运算性能将大幅下降，极大程度上限制了算法的应用。针对此问题，本文提出了犹豫度恒定的中心点构造方法，主要步骤有：

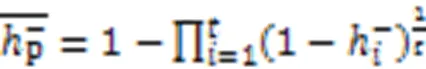
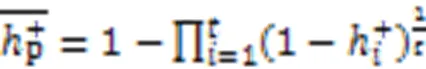
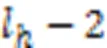
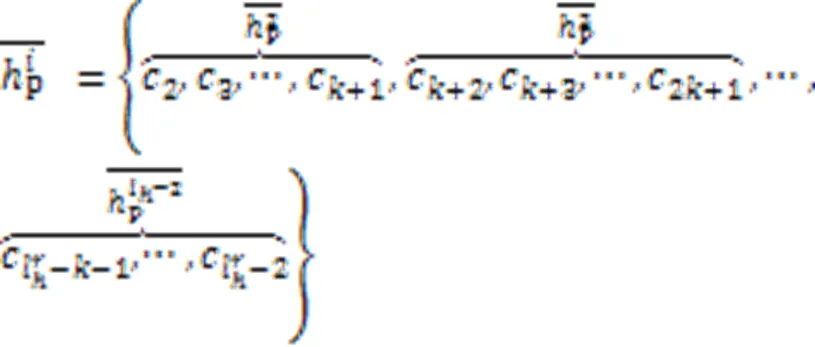
构造中心点的具体实现过程如算法3所示。

算法3 聚类中心的构造算法。

4） 根据式（14）计算中间元素

5） 中间元素排序

repeat

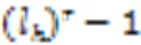
for=todo

分别找出最大值和最小值对应的下标

end for

将最大值放在最后，最小值放在最前

until （<）

end for

2.5　AHCHF流程

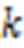
算法4 AHCHF。

3） 聚类

repeat

根据式（4）计算各簇中心之间的加权距离

end for

=-1

3 实验与结果分析

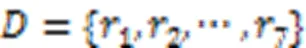
表1犹豫模糊对象集

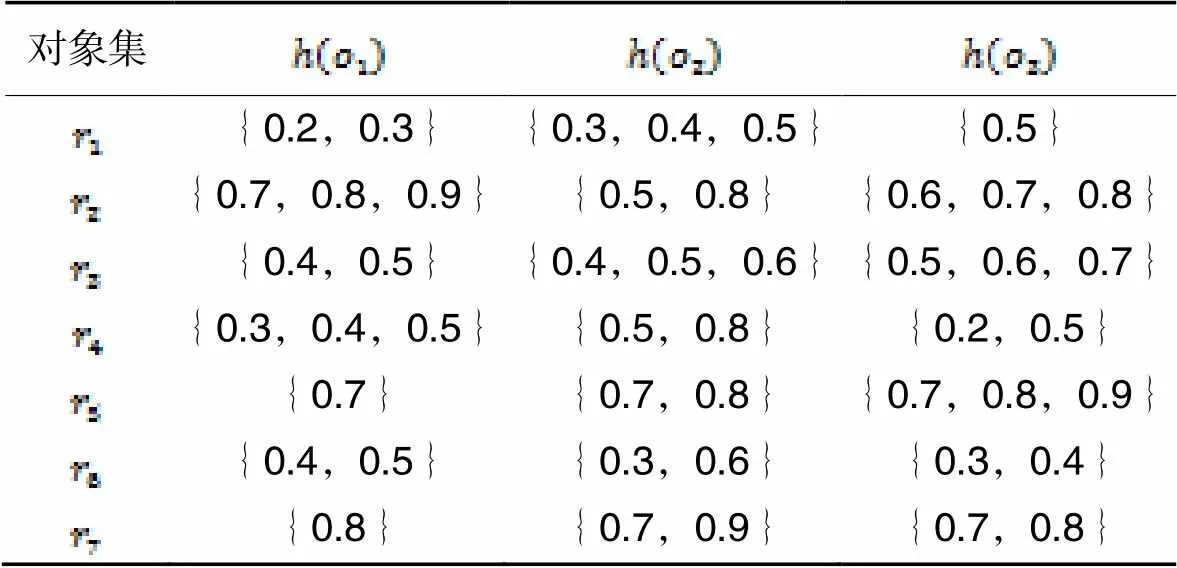
Tab.1　Hesitant fuzzy object sets

为了计算犹豫模糊对象的加权距离，需要扩充犹豫度小的数据对象。取犹豫模糊元素的平均值对它补充，扩充后的犹豫模糊集如表2所示。

表2扩充后的犹豫模糊对象集

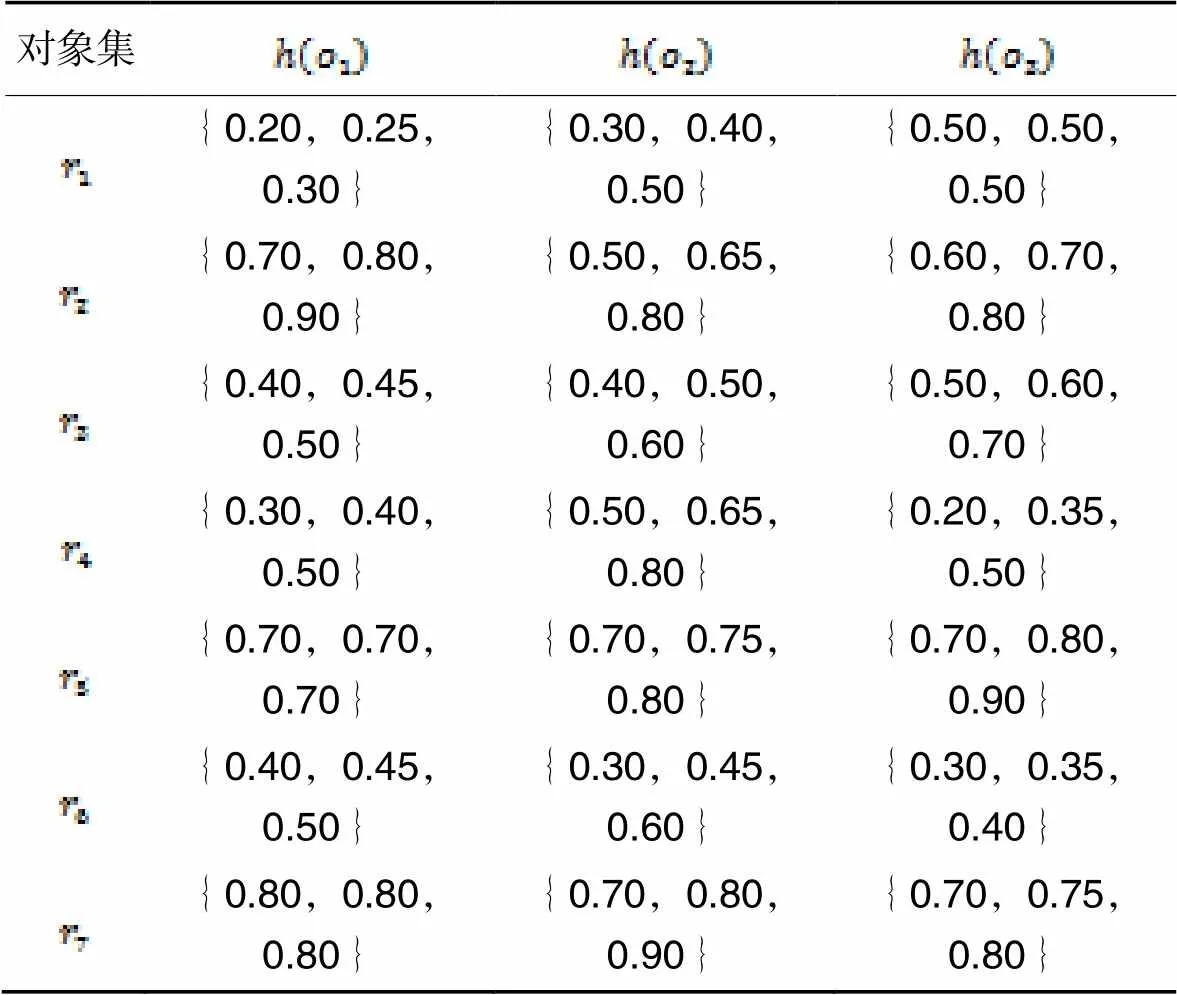
Tab.2　Expanded hesitant fuzzy object sets

表3不同方法计算的属性权重

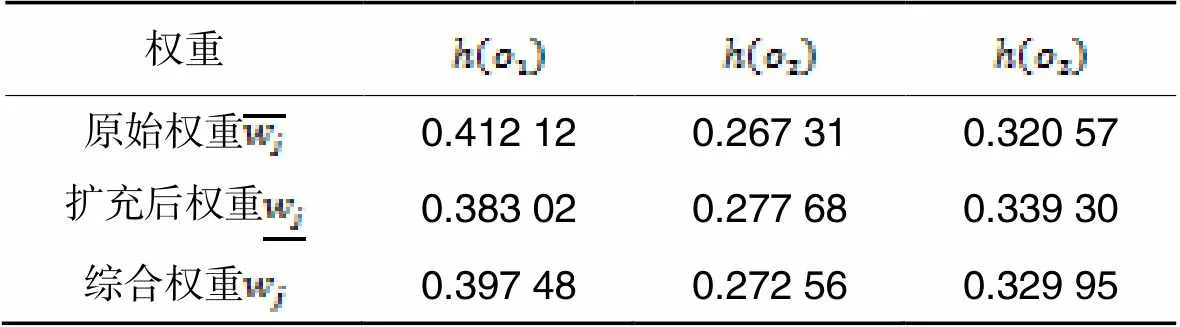
Tab.3　Attribute weights calculated by different methods

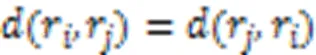
表4犹豫模糊对象之间距离

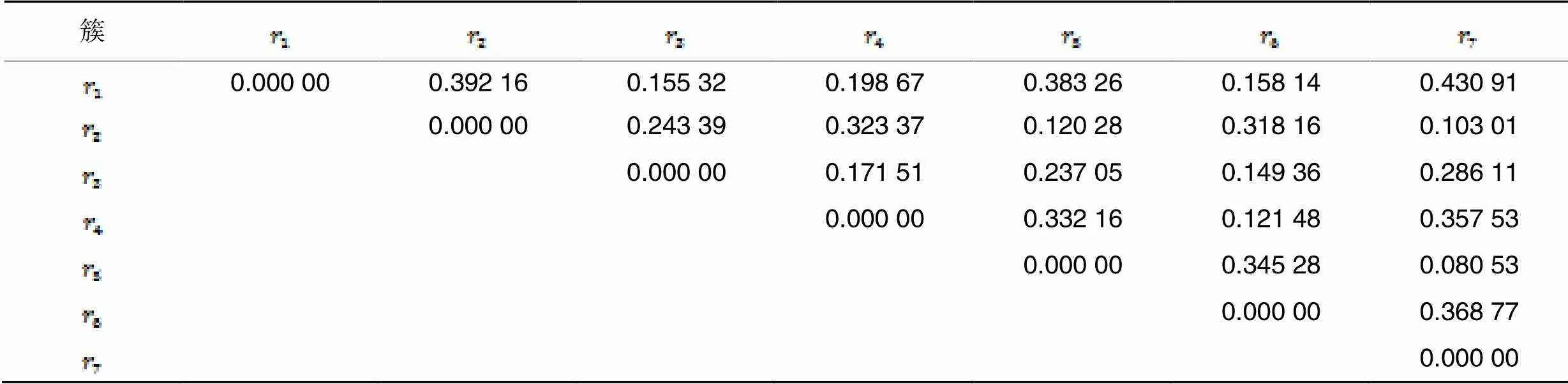
Tab.4　Distance among hesitation fuzzy objects

表5不同算法的聚类结果对比

Tab.5　Comparison of clustering results by different algorithms

3.1　聚类结果分析

为了说明AHCHF的聚类效果，引入轮廓系数（Silhouette Coefficient， SC）评价指标。SC值越大，聚类效果越好。

1）不同算法之间对比。

将本文提出的AHCHF与经典的HFHC［17］和较新的层次聚类算法FHCA［21］进行对比。当犹豫度不相同时，HFHC和FHCA采用悲观方法扩充。结果如表5所示，对应的轮廓系数如表6所示。

由表5可知，3种算法的聚类效果相似，仅有细小差异。当聚成4类和5类时，AHCHF的聚类结果与FHCA的结果相同，与HFHC略有不同；当聚成3类时，AHCHF聚类结果与HFHC的结果相同，与FHCA稍有不同。

由表6可知，AHCHF的轮廓系数均值最大，说明聚类效果整体最优，相较于HFHC和FHCA，分别提升了23.99%和9.28%。导致聚类效果提升的原因有两个：一是犹豫度采用不同的扩充方式，HFHC和FHCA采用悲观扩充，而AHCHF采用平均值扩充；二是采用的权重不同，HFHC取平均主观权重，FHCA使用客观权重，但它没有考虑犹豫度扩充后信息量的改变，而AHCHF采用综合权重，结果更客观合理。

2）不同扩充方法之间对比。

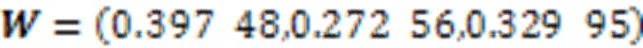
表6不同算法的轮廓系数均值

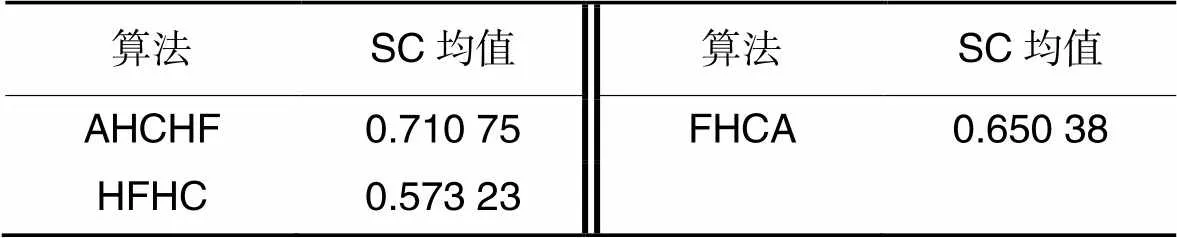
Tab.6　Mean silhouette coefficients of different algorithms

表7本文算法在不同扩充方法下的聚类结果对比

Tab.7　Comparison of clustering results by proposed algorithm under different expansion methods

表8本文算法在不同扩充方法下的轮廓系数均值

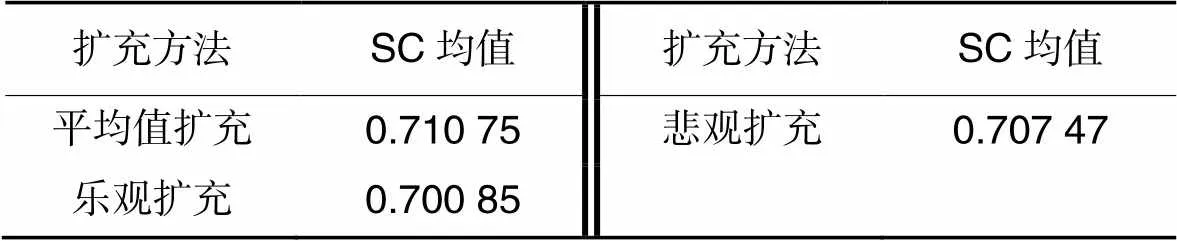
Tab.8　Mean silhouette coefficients of proposed algorithm under different expansion methods

由表8可知，平均值扩充下的轮廓系数均值最大，悲观扩充下的轮廓系数均值最小。3种扩充方法的聚类效果不相同，导致不相同的原因是不同扩充方法使犹豫模糊集的信息熵发生了不同程度信息失真：采用悲观扩充，扩充前后的信息熵变化较大，信息失真较严重；采用乐观扩充，扩充前后的信息熵变化较小，信息失真较轻；而采用平均值扩充，扩充前后的信息熵保持不变，信息未失真。可见，采用平均值扩充得到的聚类结果更合理。

3.2　簇中心点的比较

表9不同算法的中心距离对比

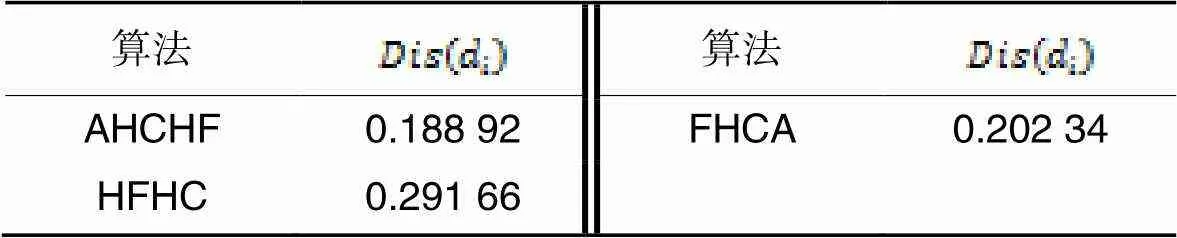
Tab.9　Comparison of center distance of different algorithms

3.3　属性权重分析

由表10可知，综合权重与主观权重2的结果完全相同，与主观权重1和主观权重3的结果有差异。在簇数为4时，综合权重的结果与主观权重3的结果不同。在簇数为3时，综合权重的结果与主观权重1和主观权重3的结果均不同。

由表11可知，主观权重2的轮廓系数均值最大，其次是综合权重，说明两种权重的聚类效果较好。主观权重1和主观权重3的轮廓系数均值较小，说明聚类效果也较差。导致聚类效果不同的原因是主观权重1认为每个属性同等重要，每个属性权重相等；事实上属性之间存在差别，重要性必然各不相同。主观权重3的第1个属性的权重值过小，对加权距离产生较大影响，使得聚类结果发生了变化；而综合权重既考虑了属性之间的重要程度，又考虑了数据扩充前后的变化情况，客观性更强，聚类结果更合理。

表10不同权重下的聚类结果对比

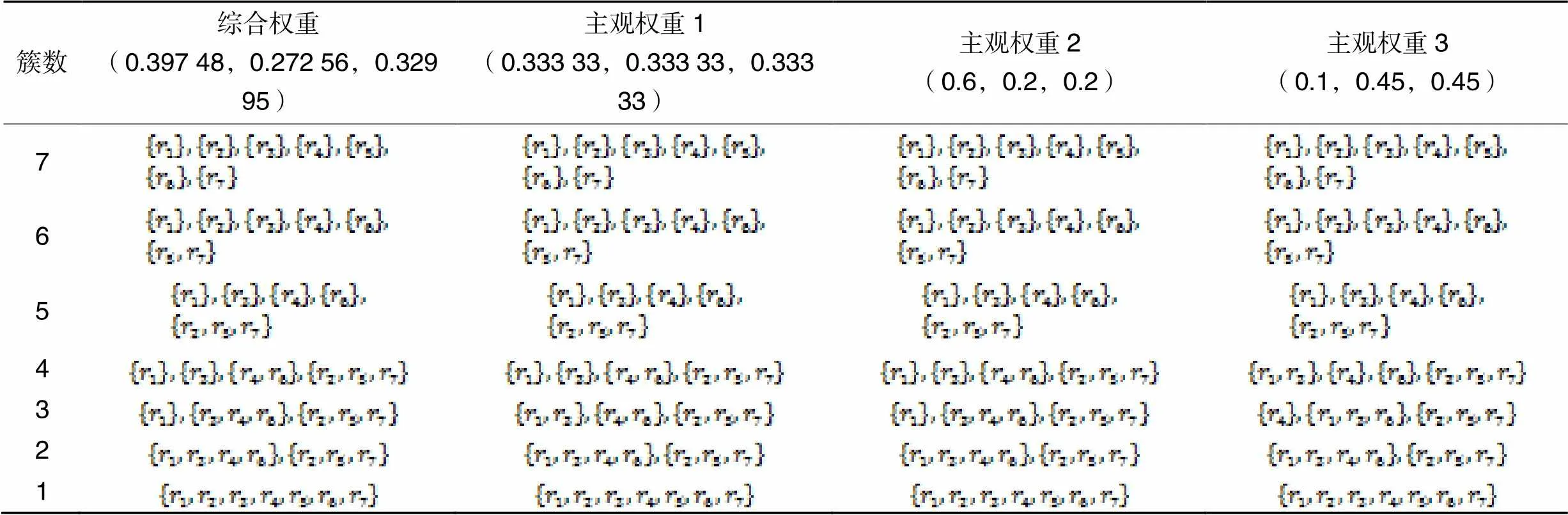
Tab.10　Comparison of clustering results under different weights

表11不同权重下的轮廓系数均值

Tab.11　Mean silhouette coefficients under different weights

3.4　复杂度分析

为验证AHCHF的实用性，从时间复杂度和空间复杂度进行了分析。算法的测试环境为64位Windows 7操作系统，Intel core i7-6500 2.5 GHz，内存为8 GB，测试平台为C# 4.0开发平台。

1）时间复杂度分析。

表12不同算法的聚类时间对比

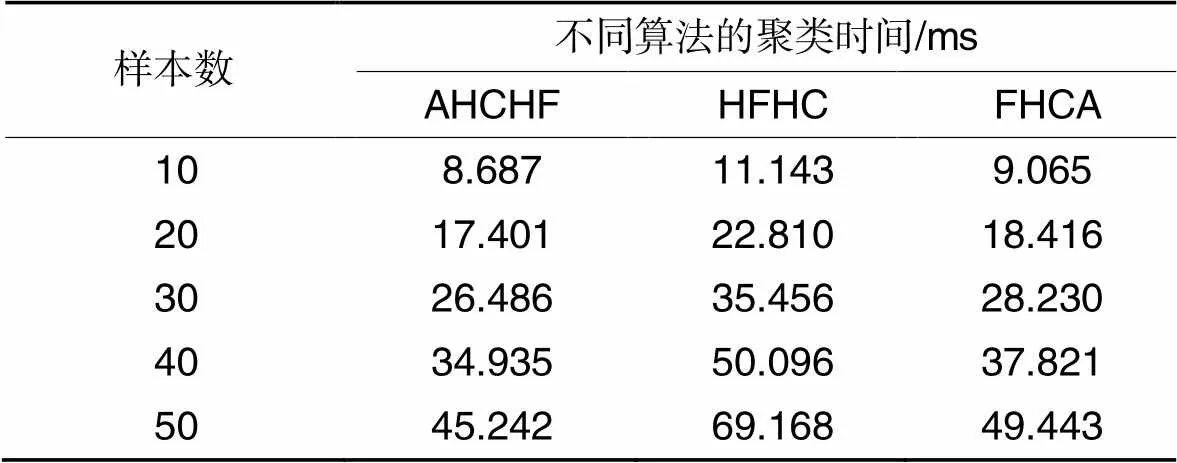
Tab.12　Comparison of clustering time among different algorithms

由表12可知，在样本数为10时，AHCHF相较于HFHC和FHCA，运行时间缩短了22.04%和4.17%；样本数的增加到50时，运行时间缩短了34.59%和8.50%；平均缩短了27.18%和6.40%。随着样本数的增加，HFHC和FHCA的运行时间均高于AHCHF，主要原因是HFHC在合并对象后，新中心点的犹豫度呈指数级增长，计算中心点与其他对象的距离时需要扩充犹豫度，导致程序频繁申请和释放空间，增加了时间消耗；同样地，FHCA在计算中心点过程更繁琐，在总体运行时间多于AHCHF。

2）空间复杂度分析。

由表13可知，在最好情况下，3种算法的空间复杂度相同；当数据对象的犹豫度大于1时，FHCA与AHCHF呈线性增长，而HFHC呈指数级增长。

表13不同算法的空间复杂度对比

Tab.13　Comparison of spatial complexity among different algorithms

从上述时间复杂度和空间复杂度分析可知，AHCHF减少了聚类时间，并将空间的复杂度从指数级降低至线性级，较好地提升了聚类性能。

4 结语

犹豫模糊集能体现信息的模糊性和决策者的犹豫不决，使得它的层次聚类分析更适应于现实场景。本文针对犹豫模糊聚类过程中存在的问题，提出了基于犹豫模糊集的凝聚式层次聚类算法（AHCHF）。该算法在保持信息熵不发生改变的情况下，采用犹豫模糊元的平均值扩充犹豫度，并利用犹豫模糊元的熵和最大离差确定综合客观权重，既反映扩充前的原始信息，又体现扩充后数据状态，然后优化了聚类中心点的构造方法。通过聚类效果、属性权重、中心距离和聚类时间这4个指标的对比实验，结果表明，AHCHF可以有效解决信息失真、属性权重客观性差的问题，并提升聚类效果和聚类性能。

虽然AHCHF提升了犹豫模糊集的聚类性能，但仍存在以下不足：1）综合权重过于客观，没有结合主观权重，灵敏性不强；2）中心点构造算法在处理大规模数据时的性能仍较低。以上不足是下一步工作重点；同时，进一步降低复杂度、拓展算法的应用领域也是今后努力的方向。

[1] 徐晓，丁世飞，丁玲.密度峰值聚类算法研究进展［J］.软件学报， 2022，33（5）：1800-1816.（XU X， DING S F， DING L. Survey on density peaks clustering Algorithm ［J］. Journal of Software， 2022， 33（5）： 1800-1816.）

[2] BALAKUMAR J， VIJAYARANI S. Text document clustering using artificial bee colony with bisecting-means algorithm［J］.International Journal of Advanced Research in Computer Science，2018，9（1）： 619-623.

[3] KARYPIS G， HAN E-H， KUMA R V. Chameleon： hierarchical clustering using dynamic modeling［J］. Computer， 1999， 32（8）： 68-75.

[4] SEGUNDO P S， RODRIGUEZ-LOSADA D. Robust global feature based data association with a sparse bit optimized maximum clique algorithm［J］. IEEE Transaction on Robotics， 2013， 29（5）： 1332-1339.

[5] ESTER M， KRIEGEL H P， SANDER， et al. A density-based algorithm for discovering clusters in large spatial databases with noise［C］// Proceeding of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland： AAAI Press， 1996： 226-231.

[6] ZADEH L A. Fuzzy sets［J］. Information and Control， 1965， 8（3）： 338-353.

[7] ATANASSOV K T. Intuitionistic fuzzy sets［J］. Fuzzy Sets and Systems， 1986， 20（1）： 87-96.

[8] ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning-Ⅱ ［J］. Information Sciences， 1975， 8（4）： 301-357.

[9] MENDEL J M. Uncertain Rule-based Fuzzy Logic System： Introduction and New Directions［M］. Upper Saddle River： Prentice-Hall， 2001： 56-57.

[10] DuBOIS D， PRADE H. Fuzzy Sets and Systems： Theory and Applications ［M］. Orlando： Academic Press， 1980： 35-37.

[11] DUNN J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters ［J］. Journal of Cybernetics， 1973， 3（3）： 32-57.

[12] 贺正洪，雷英杰.直觉模糊C-均值聚类算法研究［J］.控制与决策，2011，26（6）：847-850，856.（HE Z H， LEI Y J. Research on intuitionistic fuzzy C-means clustering algorithm［J］. Control and Decision， 2011， 26（6）： 847-850，856.）

[13] XIANG T， GONG S. Spectral clustering with eigenvector selection［J］. Pattern Recognition， 2008， 41（3）： 1012-1029.

[14] 刘怡俊，龙锦涛，杨晓君.基于多层二部图的高光谱模糊聚类算法［J］.计算机应用研究，2023，40（4）：1246-1249.（LIU Y J， LONG J T， YANG X J. Fuzzy clustering based on hierarchical bipartite graph for large scale hyperspectral image［J］. Application Research of Computers， 2022， 40（4）： 1246-1249.）

[15] 耿新青，王正欧.基于增量式模糊聚类算法的文本挖掘［J］.南京理工大学学报（自然科学版），2022，46（5）：579-585，593.（GENG X Q， WANG Z O. Text mining based on incremental fuzzy clustering algorithm［J］. Journal of Nanjing University of Science and Technology， 2022， 46（5）： 579-585， 593.）

[16] 徐晓，丁世飞，孙统风，等.基于网格筛选的大规模密度峰值聚类算法［J］.计算机研究与发展，2018，55（11）：2419-2429.（XU X， DING S F， SUN T F， et al. Large-scale density peaks clustering algorithm based on grid screening［J］. Journal of Computer Research and Development， 2018， 55（11）： 2419-2429.）

[17] TORRA V. Hesitant fuzzy sets［J］. International Journal of Intelligent Systems， 2010， 25（6）： 529-539.

[18] XU Z， XIA M. Distance and similarity measures for hesitant fuzzy sets ［J］. Information Sciences， 2011， 18（11）： 2128-2138.

[19] CHEN N， XU Z S， XIA M M. Hierarchical hesitant fuzzy-means clustering algorithm［J］. Applied Mathematics， 2014， 29： 1-17.

[20] ZHANG X L， XU Z S. Hesitant fuzzy agglomerative hierarchical clustering algorithms［J］. International Journal of Systems Science， 2013， 46（3）： 562-576.

[21] 王志飞，陆亿红.凝聚中心犹豫度恒定的模糊层次聚类算法［J］.小型微型计算机系统，2021，42（1）：20-26.（WANG Z F， LU Y H. Fuzzy hierarchical clustering algorithm with constant hesitation of agglomeration center［J］. Journal of Chinese Computer Systems， 2021， 42（1）： 20-26.）

[22] 张煜，陆亿红，黄德才.基于密度峰值的加权犹豫模糊聚类算法［J］.计算机科学，2021，48（1）：145-151.（ZHANG Y， LU Y H， HUANG D C. Weighted hesitant fuzzy clustering based on density peaks［J］. Computer Science， 2021， 48（1）： 145-151.）

[23] 孙爽爽，黄德才，陆亿红.犹豫模糊数据对象集的谱聚类算法［J］.小型微型计算机系统，2023，44（2）：225-231.（SUN S S， HUANG D C， LU Y H. Spectral clustering algorithm for hesitating fuzzy data object set［J］. Journal of Chinese Computer Systems， 2023， 44（2）： 225-231.）

[24] 邓小燕.犹豫模糊核C-均值聚类用于数据库系统选择［J］.控制工程，2020，27（1）：182-187.（DENG X Y. Hesitant fuzzy kernel C-means clustering for database system selection［J］. Control Engineering of China， 2020， 27（1）： 182-187.）

[25] 闫菲菲，魏翠萍，任智亮.犹豫模糊集的熵［J］.数学的实践与认识， 2018，48（14）：243-250.（YAN F F， WEI C P， REN Z L. Entropy measure for hesitant fuzzy sets［J］. Mathematics in Practice and Theory， 2018， 48（14）： 243-250.）

[26] XU Z， ZHANG X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information［J］. Knowledge-Based Systems， 2013， 52： 53-64.

Agglomerative hierarchical clustering algorithm based on hesitant fuzzy set

LI Wenquan*， MAO Yimin， PENG Xindong

（，，512005，）

Aiming at the problems of information distortion， poor objectivity of attribute weights， and high time complexity in hesitant fuzzy clustering analysis， an Agglomerative Hierarchical Clustering algorithm based on Hesitant Fuzzy set （AHCHF） was proposed. Firstly， the average value of hesitancy fuzzy elements was used to expand the data object with small hesitation. Secondly， the weights of data object before and after expansion were calculated by using the original information entropy and internal maximum difference， and the comprehensive attribute weight was determined according to the minimum discrimination information between the two weight vectors. Finally， with the goal of making the sum of weighted distances smaller， a center point construction method with constant hesitation was given. Experimental results on specific examples and synthetic datasets show that compared with the classic Hesitant Fuzzy Hierarchical Clustering algorithm （HFHC） and the recent Fuzzy Hierarchical Clustering Algorithm （FHCA）， the proposed AHCHF increases the mean Silhouette Coefficient （SC） by 23.99% and 9.28% respectively， and shortens the running time by 27.18% and 6.40% averagely and respectively， proving that the proposed algorithm can effectively solve the problems of information distortion and poor objectivity of attribute weights， and improve the clustering effect and performance well.

hesitant fuzzy set; clustering analysis; hesitation; data mining; fuzzy entropy

This work is partially supported by National Natural Science Foundation of China （62006155）， Scientific Research Project of Department of Education of Guangdong Province （2022ZDJS048）， Characteristic Innovation Project in Ordinary Universities in Guangdong Province （2023KTSCX137）.

LI Wenquan， born in 1980， M. S.， associate professor. His research interests include data mining， fuzzy mathematics.

MAO Yimin， born in 1970， Ph. D.， professor. Her research interests include data mining， big data security.

PENG Xindong， born in 1990， Ph. D.， associate professor. His research interests include fuzzy mathematics， artificial intelligence.

TP391.7

A

1001-9081（2023）12-3755-09

10.11772/j.issn.1001-9081.2023010094

2023⁃02⁃07；

2023⁃05⁃05；

2023⁃05⁃08。

国家自然科学基金资助项目（62006155）；广东省教育厅科研项目（2022ZDJS048）；广东省普通高校特色创新类项目（2023KTSCX137）。

李文全（1980—），男，江西龙南人，副教授，硕士，主要研究方向：数据挖掘、模糊数学；毛伊敏（1970—），女，新疆伊犁人，教授，博士，主要研究方向：数据挖掘、大数据安全；彭新东（1990—），男，江西九江人，副教授，博士，主要研究方向：模糊数学、人工智能。