基于潜在因子模型在子空间上的缺失值注意力聚类算法

王啸飞，鲍胜利*，陈炯环

基于潜在因子模型在子空间上的缺失值注意力聚类算法

王啸飞1，2，鲍胜利1，2*，陈炯环1，2

（1.中国科学院 成都计算机应用研究所，成都 610041； 2.中国科学院大学，北京 100049）（∗通信作者电子邮箱 baoshengli@casit.com.cn）

针对传统聚类算法在对缺失样本进行数据填充过程中存在样本相似度难度量且填充数据质量差的问题，提出一种基于潜在因子模型（LFM）在子空间上的缺失值注意力聚类算法。首先，通过LFM将原始数据空间映射到低维子空间，降低样本的稀疏程度；其次，通过分解原空间得到的特征矩阵构建不同特征间的注意力权重图，优化子空间样本间的相似度计算方式，使样本相似度的计算更准确、泛化性更好；最后，为了降低样本相似度计算过程中过高的时间复杂度，设计一种多指针的注意力权重图进行优化。在4个按比例随机缺失的数据集上进行实验。在Hand-digits数据集上，相较于面向高维特征缺失数据的K近邻插补子空间聚类（KISC）算法，在数据缺失比例为10%的情况下，所提算法的聚类准确度（ACC）提高了2.33个百分点，归一化互信息（NMI）提高了2.77个百分点，在数据缺失比例为20%的情况下，所提算法的ACC提高了0.39个百分点，NMI提高了1.33个百分点，验证了所提算法的有效性。

潜在因子模型；缺失值；注意力机制；聚类算法；子空间

0 引言

随着互联网的快速发展以及企业数据业务的大规模扩张，数据资源呈现爆炸式增长的趋势，对数据挖掘、信息过滤和搜索的研究得到了广泛关注。聚类算法作为数据挖掘技术的一种重要形式，能够根据相似度将一组数据（通常表现成一组数据张量或者多维数据空间当中的点集）聚类成簇。同一个簇内的数据密切相关，不同簇内的数据存在一定的差异［1］。

聚类算法作为一种无监督的机器学习算法，可以在缺少先验信息的条件下，通过计算样本间的相似度对数据进行聚类。目前常见的聚类算法包括K均值（K-means）聚类算法［2］、高斯模型聚类［3］、DBSCAN（Density-Based Spatial Clustering of Applications with Noise）［4］、层次聚类［5］和子空间聚类［6］。目前聚类算法被广泛应用到多个领域，如生物医学分析［7］、推荐系统［8］、工程优化和社交网络［9］等。

聚类算法在聚类过程中需要衡量数据样本间的相似程度，尽可能地保证相似样本分类在一个簇；但是在现实世界的数据收集过程中，底层数据通常不完整，存在部分缺失值样本。缺失值产生的原因可能有多种：1）人为因素，例如在收集调查的数据集中，调查参与的人员可能拒绝回答或者忽略某些敏感问题；2）非人为因素，如设备的故障、不正确的测量、数据采集过程中存在限制或数据的损坏都会导致产生缺失数据［10］。文献［11］中阐述了数据的缺失是聚类算法过程中常见的一类数据质量问题，有效缺失值填充可以减少数据缺失造成的聚类错误，提高聚类的准确度。如果采用不恰当的填充方式，则数据填充只是为了在算法上运行缺失数据，对提高算法准确度并没有帮助；如果算法准确度较低，则数据填充对后续工作也没有帮助，仍然存在数据质量问题。对存在缺失值的样本进行聚类的结果通常不准确，因为样本间的相似度度量受缺失值的影响导致样本分类错误。为了提高聚类算法准确度，解决数据质量问题，使用聚类算法对带有缺失值的数据进行聚类，准确衡量缺失数据中样本的相似度就显得尤为重要。

对于缺失数据的处理，比较简单且常用的方式有直接删除或者不处理缺失值；但是在聚类过程中必然会使样本相似度的计算准确率降低，导致聚类的精度降低。目前应用较为广泛的数据插补法主要有特殊值替换（均值替换、0替换和最大最小值替换等）、多重插补法、K最近邻（K-Nearest Neighbors， KNN）插补法、期望最大化（Expectation Maximization， EM）插补法和其他机器学习算法等［12］。

针对数据不完整的情况，对缺失数据进行聚类分析引起了国内外学者的广泛讨论。Albayrak等［13］通过极大似然估计填充缺失数据，但需要一部分的完整数据进行聚类，再对缺失数据进行处理；如果数据的缺失位分布均匀，将很难筛选完整的数据进行建模。Pattanodom等［14］通过随机填充缺失数据构建不同的聚类模型，再衡量模型的效果以筛选最佳的填充方式；然而该方法构建的模型可解释性很难被评估，且对计算量的要求过高，如果数据规模较大，将产生大量的子模型。Huayan等［15］通过EM算法结合K-means算法处理缺失数据，但是EM算法存在收敛慢和对初始化依赖较严重的缺点，所以存在较大的不稳定性。乔永坚等［16］提出了一种面向高维特征缺失数据的KNN插补子空间聚类（KNN Interpolation Subspace Clustering， KISC）算法，利用数据子空间的近邻关系填充数据；然而在样本相似度计算上仅计算了子空间中系数矩阵的欧氏距离进行填充，并未考虑基数矩阵的关联关系。王一棠等［17］采用了模糊聚类和非线性回归插补的算法填充缺失数据，针对盾构机数据的效果良好；但是应用具备一定的领域限制，且实现较复杂。

针对以上算法存在的问题，本文提出了一种基于潜在因子模型（Latent Factor Model， LFM）在子空间上的缺失值注意力聚类算法。LFM结合矩阵分解可以很好地处理数据稀疏问题［18］。该算法主要分为以下几个部分：1）针对缺失数据样本间相似度难以度量的问题，通过LFM将原始数据空间映射到子空间，缓解样本的稀疏性，且子空间包含样本的结构特征信息，使得样本相似度得以计算且具备一定可解释性。2）在样本相似度计算方式上引入特征矩阵进行权重注意力分配，使得样本相似度的度量方式更精确，插补的泛化性更好。3）为了缓解在特征点对点相似度计算方式上高额的时间复杂度问题，改进了注意力权重矩阵的结构，使时间复杂度达到了指数级别的优化。

1 基于LFM的缺失值注意力聚类算法

1.1　问题定义

表1符号和定义

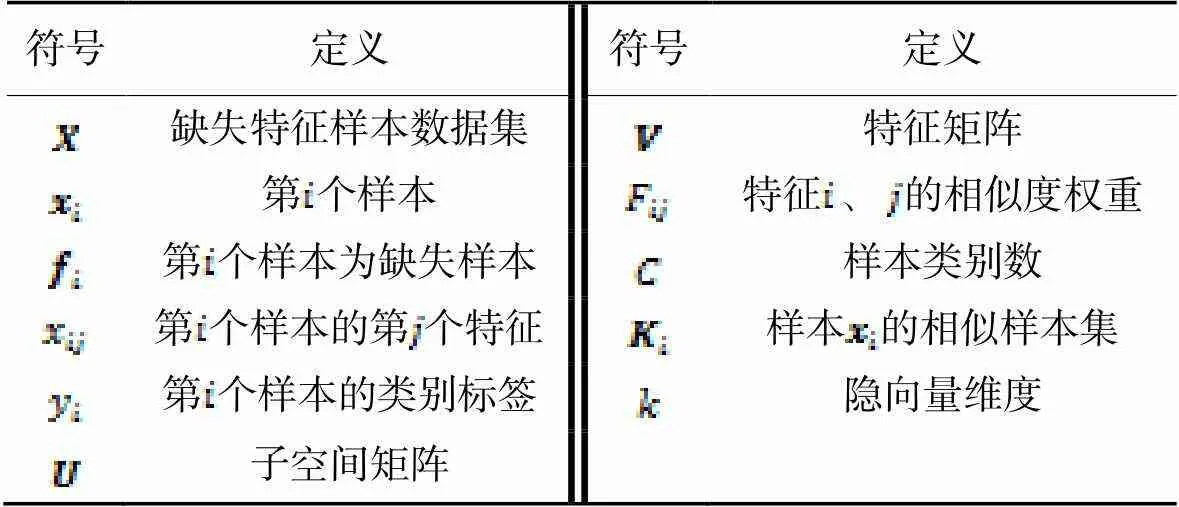
Tab.1　Symbols and definitions

1.2　算法框架

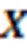
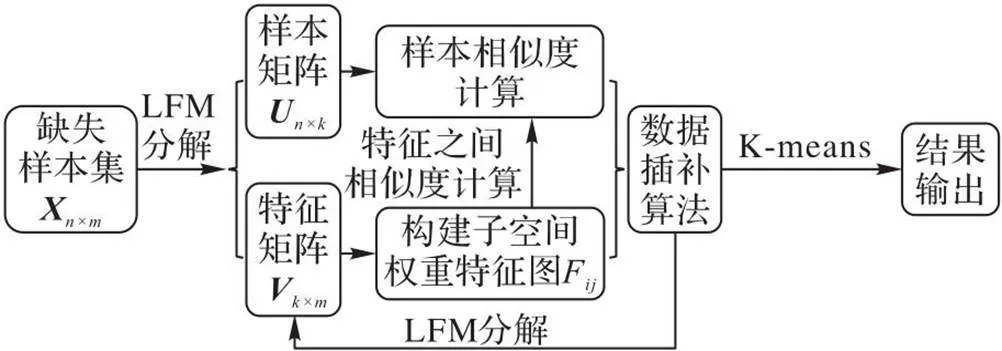
图1　本文算法的框架

1.3　LFM子空间分解

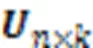
1.3.1求解方法

1.3.2优化方法

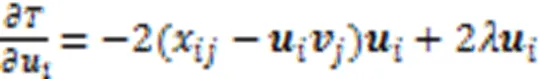
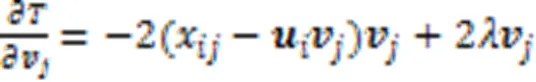
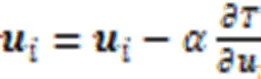
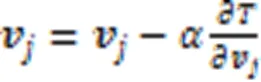
1.4　样本间的权重注意力相似度算法

1.4.1特征相似度权重图

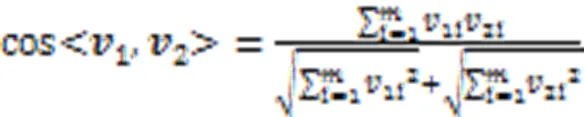
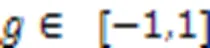
通过计算不同特征的余弦相似度可以得到特征间的注意力权重值，不同特征的注意力权重可以构建一个样本注意力权重矩阵，它的结构如图2所示。

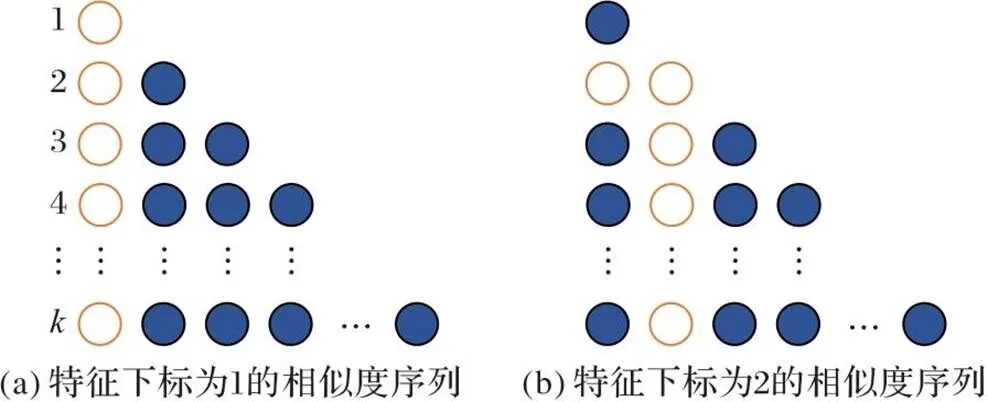
图2　样本注意力权重矩阵的结构

1.4.2样本注意力相似度计算方法

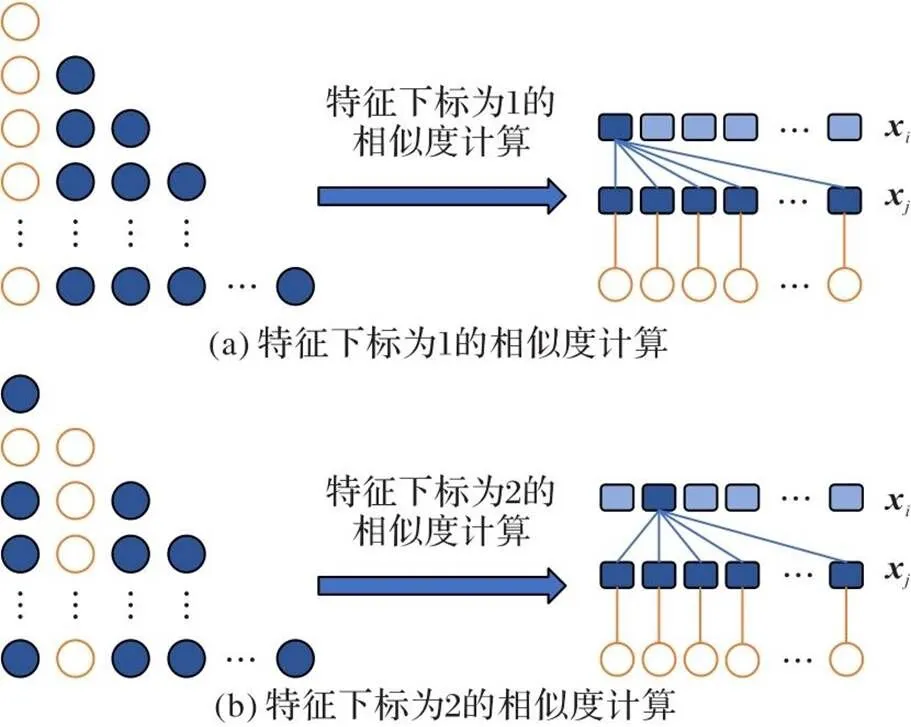
图3　样本相似度计算方式

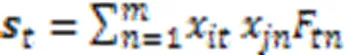
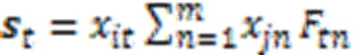
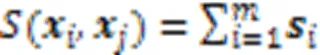
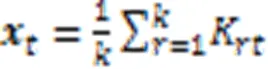
如果相似集对应位置存在缺失，则计算公式如式（13）所示：

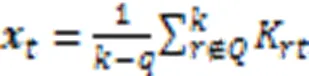
1.5　特征权重图的结构优化

算法1 相似样本集算法。

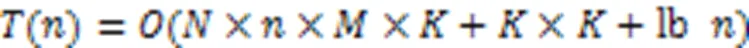
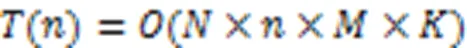
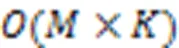
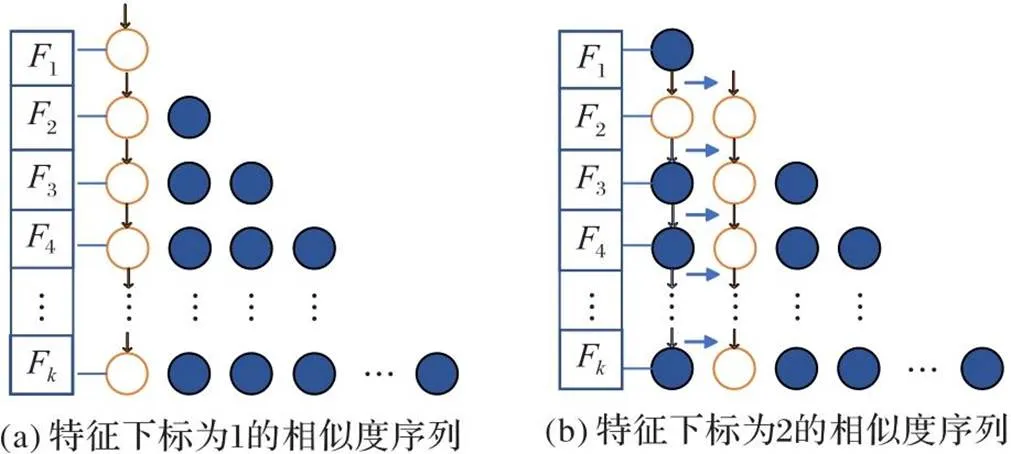
图4　多指针相似度权重图

2 实验与结果分析

2.1　实验数据

实验通过4个数据集验证本文算法的有效性，包括两个图像分类数据集和两个小样本标准分类数据集，数据集信息如表2所示。

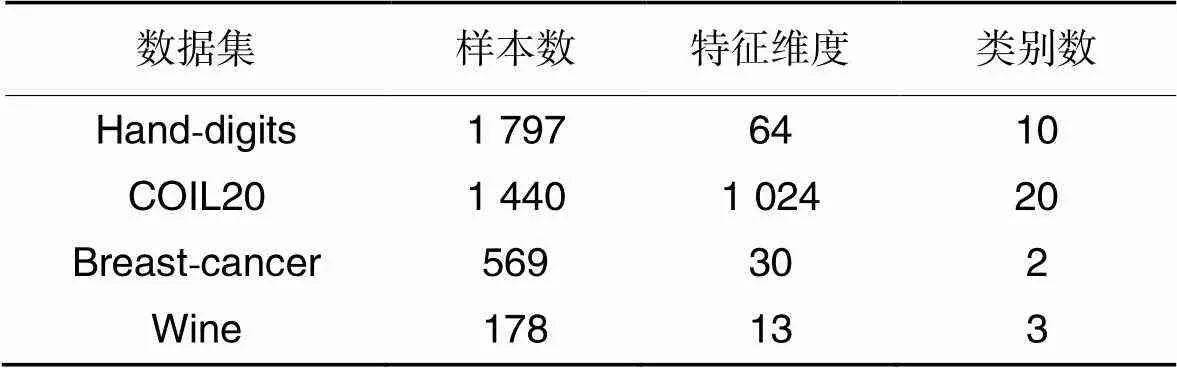
表2　数据集信息

其中Hand-digits和COIL20为两个被广泛使用的图像分类数据集，分别为手写数字的图像数据集和多个物体不同角度拍摄的图像数据集［16］。Breast-cancer和Wine为Sklearn开源机器学习工具库中的标准分类数据集。

2.2　实验设置和说明

实验在Ubuntu18.04，CPU 2.90 GHz 16 GB内存 GPU RTX3060 12 GB显存上进行，其中深度学习框架采用Torch，对数据的预处理和分析采用numpy和pandas进行。

同时为了验证多指针相似度权重图对算法时间复杂度的提升，通过计算相似度算法每一个epoch数据插补的运行时间进行衡量，最终结果取10次运行时间的平均值。

2.3　评价指标

为了充分验证算法的有效性，实验选用聚类准确度（Accuracy，ACC）和归一化互信息（Normalized Mutual Information， NMI）作为评测指标，其中：ACC可以直接衡量聚类的准确度，是常用的聚类度量指标；相较于ACC，NMI通过比较两个聚类结果的相似程度，它的值域是［0，1］，且NMI值不受簇类标签排列的影响［22］。NMI的计算公式如式（16）所示：

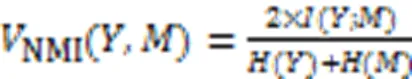
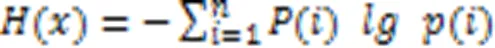
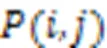
2.4　实验结果和分析

表3展示了不同数据集分别在ACC和NMI指标上的实验结果。

表3不同算法聚类结果的ACC和NMI比较 单位：%

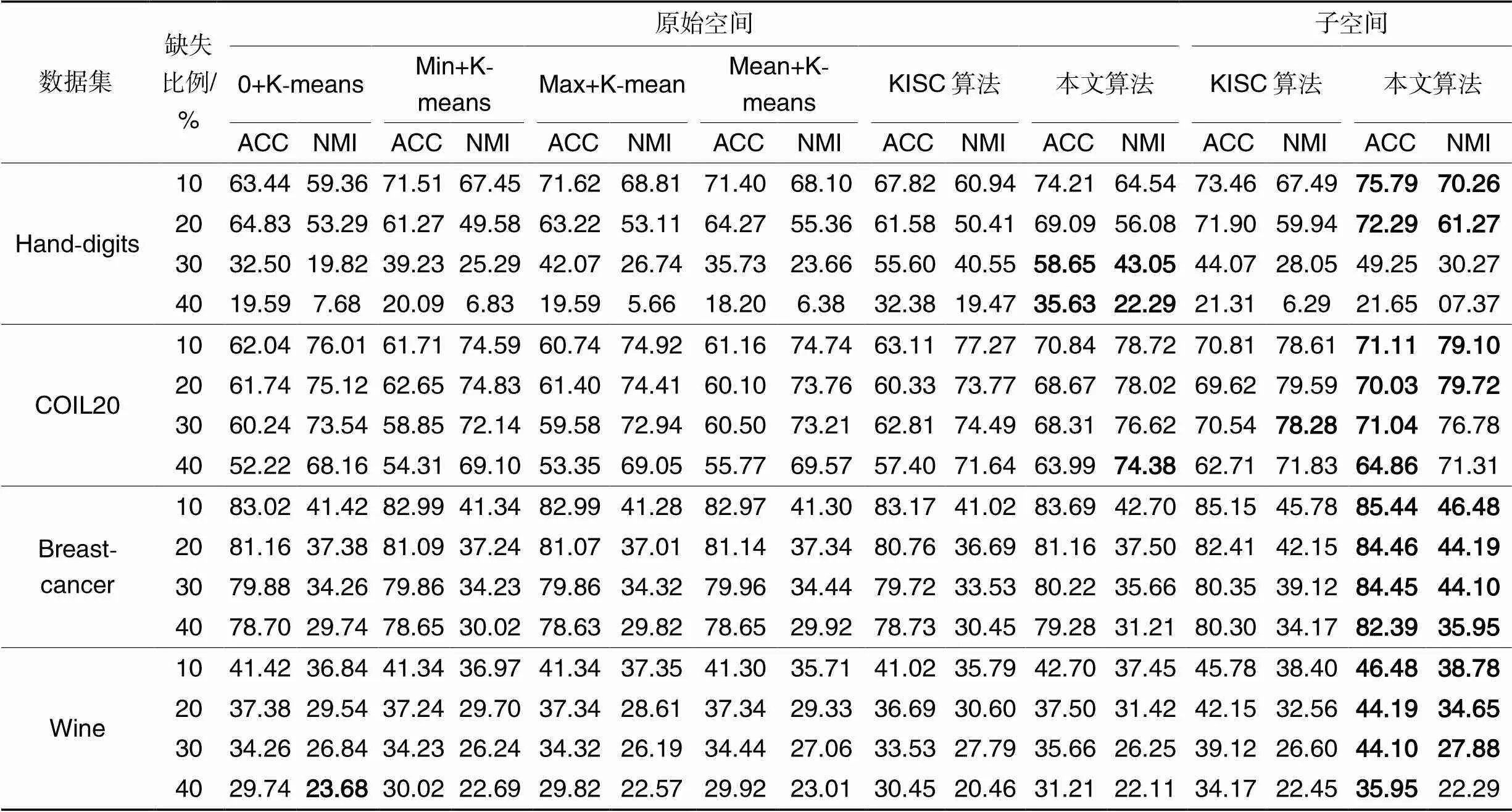
Tab.3　Comparison of ACC and NMI in clustering results between different algorithms unit：%

由表3可以发现：1）在Hand-digits数据集上，当缺失比例为10%～20%时，本文算法在子空间上的ACC和NMI均高于KISC算法和特殊值填充的K-means算法；相较于次优的KISC算法，在数据缺失比例为10%的情况下，本文算法的ACC提高了2.33个百分点，NMI提高了2.77个百分点，在数据缺失比例为20%的情况下，本文算法的ACC提高了0.39个百分点，NMI提高了1.33个百分点；当缺失比例为30%～40%时，本文算法在原始空间的聚类效果优于本文算法在子空间的聚类效果，说明当缺失比例过大时，子空间的特征结构被损坏，聚类精度降低；同时，在该缺失比例下本文算法在原始空间上的聚类效果优于KISC算法和特殊值填充的K-means算法在原始空间的聚类效果，说明本文算法采用的子空间特征注意力的缺失值填充算法是有效的。2）在COIL2数据集上，本文算法在子空间上的ACC值均高于KISC算法和特殊值填充的K-means算法，说明了本文算法的先进性；但是NMI指标在缺失比例为30%时，本文算法相较于KISC算法NMI指标精度有所下降，在缺失比例为40%时，本文算法在原始空间上的NMI指标最优，可以发现当缺失比例为30%时本文算法在原始空间的NMI指标和KISC算法在子空间的NMI指标差距较小，进一步说明了子空间特征注意力的缺失值填充算法的有效性。3）在Breast-cancer和Wine数据集上，本文算法的ACC值均高于KISC算法和特殊值填充的K-means算法，只有当Wine数据集缺失比例为40%时，本文算法的NMI值低于0填充的K-means算法。进一步发现，当缺失比例扩大时，本文算法和其他算法的差距逐渐缩小，如在Wine数据集上，当缺失比例位于10%～30%，本文算法的ACC和NMI指标均为最优；但当缺失比例达到40%，本文算法的NMI指标相较于K-means算法低了1.39个百分点，说明在缺失比例过大的情况下，子空间对特征的整体概括能力有所下降。所以本文算法在缺失比例位于10%～30%区间具备明显优势。

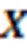
3 结语

本文针对传统聚类算法在对缺失样本进行数据填充过程中存在样本相似度难度量且填充数据质量差的问题，提出了一种基于LFM在子空间上的缺失值注意力聚类算法。该算法通过LFM解决了因为样本稀疏性导致相似距离无法度量、精度较低的问题；同时在样本相似度的计算上考虑到子空间特征矩阵之间的相关性，并将它引入相似度计算方式，提高了样本相似度计算方式的准确度和泛化性。最后在多个数据集上通过ACC和NMI指标验证了算法的有效性和可靠性。同时实验中发现：当数据缺失比例增大时，子空间对特征信息的概括能力有所降低；当数据缺失比例过大时，当前算法的聚类精度会有所下降。如何在数据缺失比例过大的情况下有效提高子空间下数据聚类算法的精度，需要进一步研究。

[1] AHALYA G，PANDEY H M. Data clustering approaches survey and analysis ［C］// Proceedings of the 2015 International Conference on Futuristic Trends on Computational Analysis and Knowledge Management. Piscataway： IEEE，2015： 532-537.

[2] XU H， YAO S， LI Q， et al. An improved K-means clustering algorithm［C］// Proceedings of the 2020 IEEE 5th International Symposium on Smart and Wireless Systems within the Conferences on Intelligent Data Acquisition and Advanced Computing Systems. Piscataway： IEEE， 2020： 1-5.

[3] 王一妹，刘辉，宋鹏，等.基于高斯混合模型聚类的风电场短期功率预测方法［J］.电力系统自动化，2021，45（7）：37-43.（WANG Y M， LIU H， SONG P， et al. Short-term power forecasting method of wind farm based on Gaussian mixture model clustering ［J］. Power System Automation， 2021，45（7）： 37-43.）

[4] JEBARI S， SMITI A， LOUATI A.AF-DBSCAN： an unsupervised automatic fuzzy clustering method based on DBSCAN approach［C］// Proceedings of the 2019 IEEE International Work Conference on Bioinspired Intelligence. Piscataway： IEEE，2019：1-6.

[5] RONG Y， LIU Y.Staged text clustering algorithm based on K-means and hierarchical agglomeration clustering［C］// Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications. Piscataway： IEEE，2020：124-127.

[6] 任丽娜，秦永彬，黄瑞章，等.基于多层子空间语义融合的深度文本聚类［J］.计算机应用研究， 2023，40（1）：70-74，79.（REN L N， QIN Y B， HUANG R Z，et al. Deep document clustering model via multi-layer subspace semantic fusion ［J］. Application Research of Computers， 2023，40（1）：70-74，79.）

[7] TAN L， GU S， WU C， et al. K-means clustering method based on node similarity in traditional Chinese medicine efficacy［C］// Proceedings of the 2020 39th Chinese Control Conference. Piscataway： IEEE，2020：742-747.

[8] YI Y. Design of intelligent recommendation APP for eco-tourism routes based on popular data clustering of points of interest［C］// Proceedings of the 2021 2nd International Conference on Smart Electronics and Communication. Piscataway： IEEE，2021： 1270-1273.

[9] SHRUTHI S， JOSE A M， ANUROOP P R. Improvisation of cluster efficiency using min-cut algorithm in social networks［C］// Proceedings of the 2017 International Conference on Communication and Signal Processing. Piscataway： IEEE，2017：1641-1644.

[10] LIU Q，HAUSWIRTH M. A provenance meta learning framework for missing data handling methods selection［C］// Proceedings of the 2020 11th IEEE Annual Ubiquitous Computing， Electronics & Mobile Communication Conference. Piscataway： IEEE，2020： 349-358.

[11] 徐宇明，陈诚，熊赟，等.APT-KNN：一种面向分类问题的高效缺失值填充算法［J］.计算机应用与软件，2011，28（4）：135-139.（XU Y M， CHEN C， XIONG Y，et al. APT-KNN： an efficient missing value imputation method oriented toward classification issue ［J］. Computer Applications and Software， 2011， 28 （4）： 135-139.）

[12] 徐鸿艳，孙云山，秦琦琳，等.缺失数据插补方法性能比较分析［J］.软件工程，2021，24（11）：11-14.（XU H Y， SUN Y S， QIN Q L， et al. Comparative analysis of the performance of interpolation methods for of missing data［J］. Software Engineering， 2021，24 （11）： 11-14.）

[13] ALBAYRAK M， TURHAN K， KURT B. A missing data imputation approach using clustering and maximum likelihood estimation［C］// Proceedings of the 2017 Medical Technologies National Congress. Piscataway：IEEE， 2017：1-4.

[14] PATTANODOM， IAM-ON N， BOONGOEN T. Clustering data with the presence of missing values by ensemble approach［C］// Proceedings of the 2016 Second Asian Conference on Defence Technology. Piscataway： IEEE， 2016： 151-156.

[15] HUAYAN S， YELI L， RUNFEI Z， et al. Accelerating EM missing data filling algorithm based on the K-means［C］// Proceedings of the 2018 4th Annual International Conference on Network and Information Systems for Computers. Piscataway： IEEE， 2018：401-406.

[16] 乔永坚，刘晓琳，白亮.面向高维特征缺失数据的K最近邻插补子空间聚类算法［J］.计算机应用，2022，42（11）：3322-3329.（QIAO Y J， LIU X L， BAI L. K-nearest neighbor interpolation subspace clustering algorithm for high-dimensional data with feature missing ［J］. Journal of Computer Application， 2022，42（11）： 3322-3329.）

[17] 王一棠，庞勇，张立勇，等.面向盾构机不完整数据的模糊聚类与非线性回归填补［J］.机械工程学报， 2023， 59（12）： 28-37.（WANG Y T， PANG Y， ZHANG L Y ，et al. Fuzzy clustering and nonlinear regression filling for incomplete data of shield machine ［J］. Journal of Mechanical Engineering， 2023， 59（12）： 28-37.）

[18] 陈晔，刘志强.基于LFM矩阵分解的推荐算法优化研究［J］.计算机工程与应用，2019，55（2）：116-120.（CHEN Y， LIU Z Q. Research on improved recommendation algorithm based on LFM matrix factorization ［J］. Computer Engineering and Applications， 2019，55（2）： 116-120.）

[19] XIONG Y， LI H. Collaborative filtering algorithm in pictures recommendation based on SVD［C］// Proceedings of the 2018 International Conference on Robots & Intelligent System. Piscataway： IEEE， 2018：262-265.

[20] 杨镆. 基于偏置LFM和LSH的混合电影推荐算法研究［D］.武汉：华中师范大学，2021：13-15.（YANG M. Research on hybrid movie recommendation algorithm based on bias LFM and LSH［D］. Wuhan： Central China Normal University， 2021： 13-15.）

[21] GUO S， LI C. Hybrid recommendation algorithm based on user behavior［C］// Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference. Piscataway： IEEE， 2020：2242-2246.

[22] 龙建武，王强.反向近邻构造连通图的聚类算法［J/OL］.计算机科学与探索：1-15 ［2023-02-07］. http：//kns.cnki.net/kcms/detail/11.5602.TP.20220930.1744.006.html.（LONG J W， WANG Q. Clustering algorithm for constructing connected graphs by reverse nearest neighbors ［J/OL］. Journal of Frontiers of Computer Science and Technology： 1-15 ［2023-02-07］. http：//kns.cnki.net/kcms/detail/11.5602.TP.20220930.1744.006.html.）

Missing value attention clustering algorithm based on latent factor model in subspace

WANG Xiaofei1，2， BAO Shengli1，2*， CHEN Jionghuan1，2

（1，，610041，；2，100049，）

To solve the problems that traditional clustering algorithms are difficult to measure the sample similarity and have poor quality of filled data in the process of filling missing samples， a missing value attention clustering algorithm based on Latent Factor Model （LFM） in subspace was proposed. First， LFM was used to map the original data space to a low dimensional subspace to reduce the sparsity of samples. Then， the attention weight graph between different features was constructed by decomposing the feature matrix obtained from the original space， and the similarity calculation method between subspace samples was optimized to make the calculation of sample similarity more accurate and more generalized. Finally， to reduce the high time complexity in the process of sample similarity calculation， a multi-pointer attention weight graph was designed for optimization. The algorithm was tested on four proportional random missing datasets. On the Hand-digits dataset， compared with the KISC （K-nearest neighbors Interpolation Subspace Clustering） algorithm for high-dimensional feature missing data， when the missing data was 10%， the Accuracy （ACC） of the proposed algorithm was improved by 2.33 percentage points and the Normalized Mutual Information （NMI） was improved by 2.77 percentage points； when the missing data was 20%， the ACC of the proposed algorithm was improved by 0.39 percentage points， and the NMI was improved by 1.33 percentage points， which verified the effectiveness of the proposed algorithm.

Latent Factor Model (LFM); missing value; attention mechanism; clustering algorithm; subspace

This work is partially supported by Western Young Scholars Project of Chinese Academy of Sciences （RRJZ2021003）.

WANG Xiaofei， born in 1997， M. S. candidate. His research interests include machine learning， recommendation algorithm.

BAO Shengli， born in 1973， Ph. D.， research fellow， His research interests include software engineering， big data.

CHEN Jionghuan， born in 1998， M. S. candidate. His research interests include machine learning， big data.

TP391.1

A

1001-9081（2023）12-3772-07

10.11772/j.issn.1001-9081.2022121838

2022⁃12⁃12；

2023⁃02⁃13；

2023⁃02⁃16。

中国科学院西部青年学者项目（RRJZ2021003）。

王啸飞（1997—），男，湖南慈利人，硕士研究生，主要研究方向：机器学习、推荐算法；鲍胜利（1973—），男，安徽黄山人，研究员，博士，主要研究方向：软件工程、大数据；陈炯环（1998—），男，山东潍坊人，硕士研究生，主要研究方向：机器学习、大数据。