也谈数学表达能力的培养

摘"要：学生只有学会用数学语言进行思考、交流和解决问题，才能更好地进行个性表达，最终发展数学思维。在教学中，培养学生的数学表达能力的具体举措包括：从感悟到勾连，丰富表达的方式；从独立到整体，明确表达的路径；从需要到运用，彰显表达的价值。

关键词：小学数学；数学表达；方式；路径；价值

数学为人们提供了一种描述现实世界的表达方式。数学语言是数学思维的载体，承载着数学的基本思想。学生只有学会用数学语言进行思考、交流和解决问题，才能更好地进行个性表达，最终发展数学思维。在教学中，教师可以通过丰富表达的方式、明确表达的路径、彰显表达的价值，来培养学生的数学表达能力。

一、丰富表达的方式：从感悟到勾连

小学阶段的核心素养侧重对经验的感悟。“感”是客观事物通过感觉器官在人脑中的反映，“悟”是理解、明白的意思。如何落实学生对数学经验的感悟？教师可以在活动中搭建多元化的表达平台，引导学生有意识地运用数学语言表达现实生活中事物的性质、关系和规律，在不同的语言形式之间转换和补充，从感悟到勾连，积累活动经验，丰富数学理解。

例如，在教学苏教版小学数学四年级下册《乘法分配律》一课时，教师引导学生从直观操作、符号释义、勾连整合三个层面表达对数学规律的理解。

（一）直观操作

为了使学生理解乘法分配律等号左右两边相等的道理，教师设置了如下自主学习活动：（1）拼一拼。从三个长方形（如下页图1所示）中选出两个，拼成一个大长方形。（2）连一连。将能计算同一个大长方形面积的算式（如下页图2所示）连起来。（3）说一说。组内交流你的想法。

在动手拼一拼的过程中，学生结合图形直观地发现：有些长方形可以拼成一个大长方形是因为它们有两条相同的边。再结合“连一连”的活动，学生发现：相同的边就是算式中括号外的数。学生用算式概括面积模型，再用图形语言解释算式特征，在操作中充分感受乘法分配律的“分”与“合”，于对比中深化体验，凸显思维的形成过程。

（二）符号释义

为了增强学生的符号意识，教师引导学生用字母来概括等式的相同结构特征，并通过乘法算式的意义以及加法运算律解释乘法分配律的合理性。

最终整理得到的符号释义结果如图3所示。

从具体算式到归纳运算规律，是基于实例的符号表达，再用符号运算进行演绎推理，能够丰富学生的学习经验，提高学生的说理表达能力。

（三）勾连整合

为了让学生进一步感悟乘法分配律，建立新旧知识之间的联系，教师设置问题，让学生说一说哪里体现了乘法分配律。问题包括：（1）口算12×3。（2）篮球场的长是28米，宽是15米，它的周长是多少米？（3）四年级有6个班，五年级有4个班，每个班领24根跳绳，两个年级一共要领多少根跳绳？

熟悉的问题可以激发学生表达的积极性，更方便其将数学信息转化成数学表达式，再用文字语言解释算式意义，让数学思维更具象，使知识结构更完整。

从经验到推理再到勾连，一方面，让学生对数学事物的表达越来越明确；另一方面，使学生在丰富的感知中体会思维从抽象到具象再到抽象的过程，逐步学会用数学语言表达自己的想法，解释现实世界中的数学规律。

二、明确表达的路径：从独立到整体

数学知识具有很强的内在逻辑，是整体

（a＋b）× c

=（a＋b）＋（a＋b）＋…＋（a＋b）c个

乘法的意义

=a＋a＋…＋ac个＋b＋b＋…＋bc个

加法交换律和加法结合律

=（a＋a＋…＋a）c个＋（b＋b＋…＋b）c个

加法结合律

=a×c＋b×c

乘法的意义的、系统的、结构的。但在数学学习的过程

中，学生头脑中的知识很多时候是独立的、零散的，有时还存在模糊杂乱、混淆不清的情况。在课堂教学中，教师应设置贴近学情的探究活动，引导学生厘清知识的本质，明确表达的路径，形成条理清晰、层次分明的数学思维。

例如，在教学苏教版小学数学四年级下册《多边形的内角和》一课时，教师引导学生从三角形内角和出发，通过猜想（特殊到一般）、验证（测量、剪拼和分割）的活动探究多边形内角和，归纳方法，逐步推导得出多边形的内角和公式。具体的表达路径为：分类对比、建构模型、融会贯通。

（一）分类对比

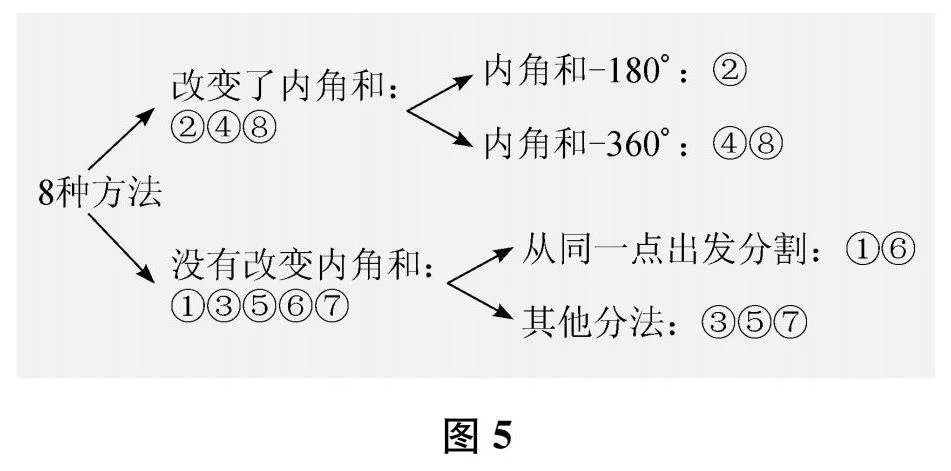
在得到任意四边形的内角和是360°后，教师重点引导学生以分割的方法继续研究五边形和六边形的内角和。在展示学生各种方法的环节，如果交流中没有问题引领，作品独立呈现，那学生的思考就无法聚焦，表达也会显得杂乱无章，不利于学生理解不同分法之间的本质与联系。实际教学中，学生主要呈现了8种分法（如图4所示）。

教师引导分步骤交流：（1）仔细观察，你能将这些不同的方法进行分类吗？（2）为什么有些分法会改变内角和？（3）如果继续研究七边形和八边形的内角和，你更愿意选择哪种方法？

学生的研究视角不同，就产生了不同的分法。在关键问题的引领下，学生通过逐级分类的方式，梳理不同分法背后的道理。然后，教师引导学生结合分类结果（如图5所示）感受：其实，每一种分割方法都是通过转化得到结果，存在相同的思维模式。进而，探索出以“三角形的内角和为180°”作为计量标准，把多边形内角和转化成若干个三角形内角和的计算方式。从解决问题的角度，条理化地表达符合知识的生长性，便于建构普适的数学模型；从思维发展的角度，结构化地表达更容易把握数学探究对象的整体性，使思维走向深入。

（二）建构模型

在研究“三角形的内角和”时，学生主要通过测量、折拼、剪拼的方法，把不同位置的3个内角想方设法合起来。虽然操作的路径不一样，但“分与合”的数学思想一脉相承。于是，在探索“四边形的内角和”时，学生也尝试运用测量、剪拼的方法，并在“分与合”思想的驱动下，衍生出分割的方式，从而简洁地表达出思考过程，得到运算结果。从具身操作到比较优化最终形成计算模型，不同的分割方式表达了相同的“分与合”体悟。这种真实的经历更能激发学生用数学语言表达方法背后的数学思想，而数学模型的建构也会在无形中滋养学生的思维。

（三）融会贯通

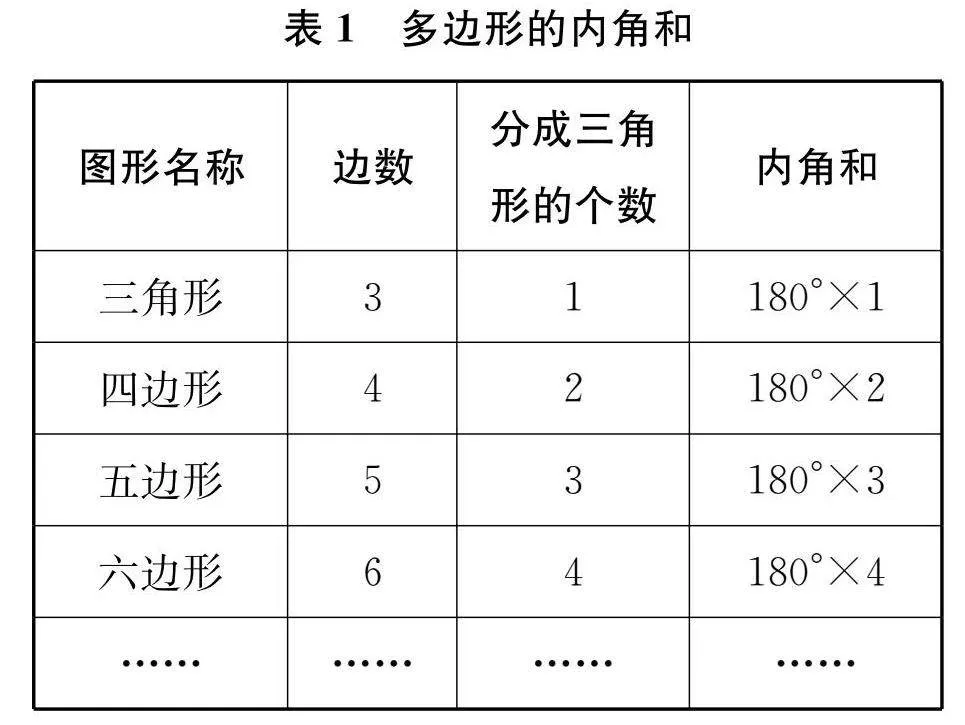
在研究“四边形的内角和”时，学生是从长方形和正方形的内角和出发，猜测任意四边形的内角和，再加以验证，这是从特殊到一般的论证过程。在探究“多边形的内角和”时，教师以表格的方式出示结果（见表1），使学生从关注具体图形到发现计算规律，体现了从简单到复杂的有序思考过程。搭建这样的学习框架，有助于增强学生合乎逻辑的表达能力，在表达中迁移经验，培养高阶的数学思维。

数学教学要关注知识、方法和能力的形成过程。因此，教师需要理清知识线索，整体贯通地设计表达路径，从个体方法到系统呈现，从点状分布到线面关联。学生真实地体验、自主地表达，才能实现方法的迁移、优化、勾连和沉淀，驱动数学思想的内化，实现数学思维的进阶。

三、彰显表达的价值：从需要到运用

数据表达是分析事物发展情况的一种量化形式。强化基于数据表达现实问题的意识，可以帮助学生积累依托数据探索事物本质、联系和规律的活动经验，形成通过数据认识事物的思维品质。

例如，在教学苏教版小学数学六年级上册《百分数的认识》一课时，教师从基于需要、整体认知、分析应用三个方面体现数学表达的意义与价值。

（一）基于需要

为了让学生产生统计需要，体会统一标准的重要性，教师设计了质量检验部门对不同品牌口罩抽样检测的情境。

教师分步出示表2：先出示三种品牌的合格数量，发现只看一组数据不能得出哪个品牌最好；再出示抽查数量，进行比较，发现只比不合格的数量不合理，关键要找到合格数量与抽查数量的关系。

在分析数据时，学生的数学感觉与思维产生碰撞，体会到由绝对到相对的过程。“百分数”的出现，将数量关系与比较结果表达得既直观又方便。基于统计需求的数据表达，能帮助学生自主建构知识，锻炼思维的深刻性。

（二）整体认知

百分数的价值在于其能精准表达两个数量之间的倍比关系。为了深化对百分数的理解，规范百分数意义的语言表达模型，感受百分数对于描述数据的作用，沟通百分数与分数、比的联系，教师设计了有关电池电量的实际问题。

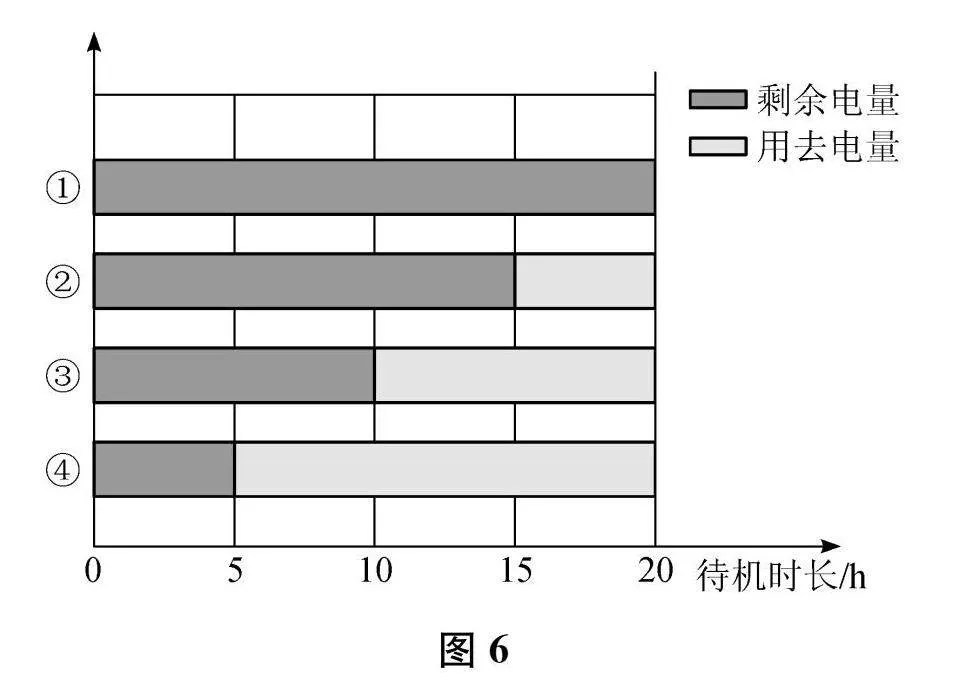
例题"（1）你能看懂图6中这些电池电量的情况吗？从图中你能看到哪些百分数？

（2）它表示什么含义？（用“""是""的百分之几”这样的句式回答）

（3）你还能看出哪些数学信息？

数学来源于生活，围绕电池电量图展开的教学为百分数的表达找到了现实支点。从数学模型、语言模板、关联旧知三个方面整体建构对百分数意义的理解与表达，促使学生在对已有认知的同化和顺应中不断发展数学思维。

（三）分析应用

统计的研究对象是随机数据，教学百分数的统计意义时要让学生知道现实世界中随机现象是普遍存在的，感受随机数据的特征以及表达随机现象发生的可能性大小。因此，教师在教学中加入了“抛硬币”的活动：小组合作，每人各抛10次，记录正面朝上的次数和反面朝上的次数，并尝试计算出相应的百分比。小组合作完成活动后，教师引导学生把个人数据、小组数据、全班数据综合对比，发现百分比越来越接近50%，最后呈现科学家试验的数据（如表3），进一步引导学生观察、思考和发表观点。

统计的思维就是用部分数据推断总体情况，在刻画不确定事件时，这种根据数据作出推断的方式就是统计的本质。在“抛硬币”试验中，通过大数据的试验，可以发现硬币正面朝上或反面朝上出现的可能性在50%附近波动，从而理解“50%”的统计意义，感受比赛中用抛硬币来决定顺序的公平性，体会数据表达对现实生活的决策价值，让思维更有内涵。

从对数据统计的需要到数据分析的运用，百分数的价值体现为能简洁准确地对数据进行刻画与表达，并帮助人们作出判断。学生完整经历了用数据解决问题的过程，逐步形成用数据表达与交流的意识，数学思维也随之不断提升。