求解逆混合变分不等式问题的动力系统方法

罗馨缘,张 欢,冯世强

(西华师范大学 数学与信息学院,四川 南充 637009)

变分不等式对于研究经济、管理和工程中出现的各种网络均衡问题具有重要作用。变分不等式的一个重要推广就是混合变分不等式(MVI),这一不等式由Lescarret[1]和Browder[2]提出,相继被众多学者研究应用。2002年,Konnov和Volostkaya[3]考虑了一般经济均衡问题和寡占均衡问题,这又被表述为混合变分不等式问题。随后,Wu和Huang[4-6]在Banach空间引入一种新的广义f-投影算子用来解决混合变分不等式问题。2006年,He等[7]首次提出了逆变分不等式,并将逆变分不等式应用于经济学中的市场均衡问题[8]。此外,在交通、电信网络问题中的一些规范问题也可以用逆变分不等式来解释[9-10]。He和Liu[11]提出了一种新的基于投影的求解逆变分不等式问题的方法,其中映射F在约束集上是余强制的。逆变分不等式的一个重要有用的推广称为逆混合变分不等式(IMVI)。2013年,Li等[12]在Hilbert空间背景下引入一个新的逆混合变分不等式,构造一个涉及广义f-投影算子的求解逆混合变分不等式的迭代算法。

本文目的有2个:首先在强单调和Lipschitz连续性的假设条件下,根据广义f-投影算子性质,研究了具有某种压缩映射的逆混合变分不等式问题解存在唯一的充分条件。进一步地,通过考虑一个动力系统来求解逆混合变分不等式问题,并且证明在强单调和Lipschitz连续性的条件下该动力系统均衡点是全局指数稳定性。

1 预备知识和基本概念

〈x′-Ax,x〉+g(x′)-g(Ax)≥0, ∀x′∈M,

(1)

式中:ri domM∩ri domg≠∅,QIMVI(A,g)的解集表示为Sol(A,g),这里ri表示相对内部,dom表示有效域。

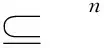
(2)

(3)

若ri domF1∩…∩ri domFm≠∅,则(3)式中的反包含关系成立。

2 解的存在性和唯一性

(4)

其中arg min表示使目标函数取最小值时的变量值,由于yG(x,y)在n上是凸的,则对于每一个x∈M和λ>0,(4)式是一个强凸问题,因此它有唯一解。 因而φλ是良定的且在M上只有一个值。

证明充分性:令Ax*=φλ(x*),则Ax*是(4)式的一个解,Ax*∈M且由引理1和引理2可得0∈λ∂G(x*,Ax*)+Ax*-Ax*+NM(Ax*),即0∈λ∂G(x*,Ax*)+NM(Ax*)。 所以,存在z∈∂G(x*,Ax*),使得0∈λz+NM(Ax*)。 因此,由法锥的定义可知,对任意的y∈M,〈-λz,y-Ax*〉≤0,即

〈z,y-Ax*〉≥0,∀y∈M。

(5)

又由于z∈∂G(x*,Ax*),则对任意的y∈M,

G(x*,y)-G(x*,Ax*)≥〈z,y-Ax*〉。

(6)

又由G(x*,Ax*)=0,结合(5)式、(6)式得G(x*,y)≥〈z,y-Ax*〉≥0。因此,对于任意的y∈M,G(x*,y)≥0,即x*是QIMVI(A,g)的一个解,x*∈Sol(A,g)。

必要性:设x*∈Sol(A,g),令y*=φλ(x*),则y*是(4)式的一个解,所以由引理2可以得到0∈λ∂G(x*,y*)+y*-Ax*+NM(y*),则存在s∈∂G(x*,y*),使得0∈λs+y*-Ax*+NM(y*)。又因为s∈∂G(x*,y*),则对y*∈M,G(x*,Ax*)-G(x*,y*)≥〈s,Ax*-y*〉。且由法锥的定义可知,对任意的y∈M,有〈Ax*-y*-λs,y-y*〉≤0。 又因为Ax*∈M,则在上式中令y=Ax*可以得到‖Ax*-y*‖2-〈λs,Ax*-y*〉≤0,即‖Ax*-y*‖2≤λG(x*,Ax*)-λG(x*,y*)=-λG(x*,y*)。 又因为x*∈Sol(A,g),所以Ax*∈M,G(x*,y*)≥0,则‖Ax*-y*‖2≤0。 且‖Ax*-y*‖2≥0,所以‖Ax*-y*‖=0,因此Ax*=y*=φλ(x*)。

备注1考虑G(x,y)=〈y-Ax,x〉+g(y)-g(Ax),其中Ax∈domg,则(4)式变为

定理2令A∶H→H是L-Lipschitz连续和γ-强单调,且存在λ>0,使得

则τ是带压缩系数的压缩映射,从而逆混合变分不等式问题QIMVI(A,g)有唯一解。

证明对任意的x,y∈H有

≤‖x-y-(Ax-Ay)‖+‖Ax-Ay-λ(x-y)‖。

(7)

又因为A是关于系数γ强单调的,则

〈x-y,Ax-Ay〉≥γ‖x-y‖2,

(8)

且A是关于L的Lipschitz连续,则

‖Ax-Ay‖≤L‖x-y‖,

(9)

所以由(8)(9)式可得

‖x-y-(Ax-Ay)‖2=‖x-y‖2-2〈x-y,Ax-Ay〉+‖Ax-Ay‖2

≤‖x-y‖2-2γ‖x-y‖2+L2‖x-y‖2

=(1-2γ+L2)‖x-y‖2。

(10)

同理可得

‖Ax-Ay-λ(x-y)‖2=‖Ax-Ay‖2-2λ〈Ax-Ay,x-y〉+λ2‖x-y‖2

≤L2‖x-y‖2-2λγ‖x-y‖2+λ2‖x-y‖2

=(L2-2λγ+λ2)‖x-y‖2。

(11)

3 动力系统

回顾以往的一般动力系统均衡点稳定性的概念

(12)

‖x(t)-x*‖≤μ‖x(0)-x*‖e-ηt,∀t≥0。

(13)

此外,称x*是全局指数稳定,如果(13)式对(12)式的所有解x(t)都成立。

因此,为了求解逆混合变分不等式问题QIMVI(A,g),考虑如下形式的动力系统

(14)

式中:β>0,Ax(t)∈domg。

若定理2的条件都满足,则逆混合变分不等式有唯一解。由定理1和定理2及动力系统(14)的定义形式可知,x*是它的唯一均衡点。

〈y-Ax*,x*〉+g(y)-g(Ax*)≥0,

因此

〈y-Ax*,λx*〉+λg(y)-λg(Ax*)≥0。

(15)

由引理3(ii)可知,对∀z∈M有〈y-Ax(t)+λx(t),z-y〉+λg(z)-λg(y)≥0,

令z=Ax*∈M代入上式不等式中则

〈y-Ax(t)+λx(t),Ax*-y〉+λg(Ax*)-λg(y)≥0。

(16)

所以由(15)(16)式相加可得〈y-Ax*,λx*-λx(t)-y+Ax(t)〉≥0,等价于〈Ax(t)-Ax*+y-Ax(t),Ax(t)-y-λ(x(t)-x*)〉≥0。因此,

λ〈y-Ax(t),x(t)-x*〉≤-‖Ax(t)-y‖2-λ〈Ax(t)-Ax*,x(t)-x*〉+〈Ax(t)-Ax*,Ax(t)-y〉。

又因为A是关于γ-强单调和L-Lipschitz连续,然后由Cauchy-Schwarz不等式可得

λ〈y-Ax(t),x(t)-x*〉≤-‖Ax(t)-y‖2-γλ‖x(t)-x*‖2+〈Ax(t)-Ax*,Ax(t)-y〉

≤-‖Ax(t)-y‖2-γλ‖x(t)-x*‖2+‖Ax(t)-Ax*‖‖Ax(t)-y‖

≤-‖Ax(t)-y‖2-γλ‖x(t)-x*‖2+L‖x(t)-x*‖‖Ax(t)-y‖

所以

(17)