双定数混合截尾下双参数指数分布的统计分析
金雪莲,李云飞
(西华师范大学 数学与信息学院,四川 南充 637009)
双参数指数分布在金融学等各个领域应用广泛,双参数指数分布的研究也取得了一些成果。李艳玲[1]讨论了双参数指数分布在定数截尾试验下的贝叶斯预测问题;田霆和刘次华[2]研究了数据缺失的情况下,双参数指数分布的Bayes估计并给出了一种近似计算方法;张娅莉和李淑玉[3]、张良超和温利民[4]、李云飞[5]研究了双参数指数分布参数的估计问题;梁米和李云飞[6]利用新的方法对双参数指数分布异常数据进行了研究;Krishna 和Goel[7]研究了双参数指数分布在随机截尾数据下的经典估计和Bayes估计;Upadhyay 和Umesh[8]利用独立先验给出双参数指数分布的Bayes估计。上述研究都是关于双参数指数分布在一些截尾场合下的讨论,但是还没有双定数混合截尾场合下的研究。因此,在双定数混合截尾场合下,对双参数指数分布进行统计分析具有一定的理论和实际意义。
双定数混合截尾试验是龙兵和张忠占[9]提出的一种新的截尾试验方案,即2个定数截尾试验方案的混合,并在此寿命试验数据下对两参数Pareto分布进行统计分析。由于在定数截尾试验中,在达到预先确定的失效样品数时,进行的寿命试验可能还没有达到规定时间,因此,可以考虑重新确定样品的失效数,提高估计精度。目前国内外关于定数截尾、双边定数截尾试验等研究较多,关于双定数混合截尾的研究较少。因此,本文将基于双定数混合截尾试验,讨论双参数指数分布尺度参数θ和可靠度函数R(x)的估计问题。
1 模型描述
双定数混合截尾试验如下:假设随机抽取n个寿命独立同分布的元件进行试验,事先确定正实数t0以及正整数m1,m2,且满足m1 将上述试验分为两种情形: 情形1:(X1:n,X2:n,…,Xm1:n),若Xm1:n≥t0; 情形2:(X1:n,X2:n,…,Xm2:n),若Xm1:n 根据第1节中寿命试验模型,利用极大似然估计(Maximum likelihood estimate,MLE)讨论双参数指数分布中尺度参数θ的估计问题。 (1) 因此,当μ已知时,尺度参数θ的置信度为100(1-α)%的置信区间为(θL,θU),其中 取θ的先验分布为逆Gamma分布IG(a,b),则其概率密度函数为: (2) 这里的超参数a>0,b>0。 当μ已知时,由(1)和(2)式可以得到θ的后验密度函数Π(θ|x*) 引理2[12-14]设x*=(x1:n,x2:n,…,xk:n)为来自某总体的双定数混合截尾数据,则有 Kano & Li 2014: Kanu Kazuo (加納和雄) & Li Xuezhu (李学竹), Sanskrit Verses from Candrakīrti’s Triśaraasaptati Cited in the Munimatālakāra, China Tibetology,vol. 22, 4-11. 这里的δ是尺度参数θ的一个估计。 定理1设x*=(x1:n,x2:n,…,xk:n)为来自双参数指数分布的双定数混合截尾数据,当μ已知时,若θ的先验分布为逆Gamma分布,则可以得到以下结论: 证明1)因为 所以 2)因为 所以 3)因为 所以 因此,在Q-对称熵损失函数下,θ的E-Bayes估计为 在Mlinex损失函数下,θ的E-Bayes估计为 在加权平方损失函数下,θ的E-Bayes估计为 定理2设x*=(x1:n,x2:n,…,xk:n)为来自双参数指数分布的双定数混合截尾数据,当μ已知时,若θ的先验分布为逆Gamma分布,则可以得到以下结论: 证明1)因为 所以 2)因为 所以 3)因为 所以 设均匀分布U(0,1)产生的相互独立随机数为r1,r2,…,rn,给定参数μ,θ的值,则xi=μ-θln(1-ri),i=1,2,…,n即为来自双参数指数分布的随机数。在样本容量n=20,30,50情形下,给定m1,m2,t0的值,取超参数(a,b)=(1,2)且在损失函数中取c=0.5,q=2。根据双定数混合截尾试验方案计算出各估计值,将以上过程重复1 000次,可以得到各个点估计的均值和平均相对误差(Mean Relative Error,MRE),计算结果见表1和表2。其中 表1 μ已知时,θ的估计Table 1 Estimate of θ when μ is given 表2 μ已知时,可靠度函数R(x)的估计(x=3)Table 2 Estimate of reliability function R(x) when μ is given (x=3) 比较表1和表2可:(1)当试验的样本容量n固定时,在3种不同损失函数下,基于双定数混合截尾试验得到的尺度参数θ和可靠度函数R(x)的估计值的MRE小于定数截尾试验下所得估计值的MRE,说明双定数混合截尾试验在此3种损失函数下可以提高尺度参数θ和可靠度函数R(x)的估计精度。(2)在双定数混合截尾试验下,根据MRE可以看出尺度参数θ和可靠度函数R(x)的Bayes估计比MLE更优。(3)随着样本容量的增加,在相同的(μ,θ)下,尺度参数θ和可靠度函数R(x)的MRE逐渐减小。 本文研究了双定数混合截尾试验和定数截尾试验下,双参数指数分布尺度参数θ和可靠度函数R(x)的MLE以及3种不同损失函数下的Bayes估计。结果表明,与定数截尾相比,双定数混合截尾试验下尺度参数θ和可靠度函数R(x)的Bayes估计和MLE更优。在双定数混合截尾试验下,尺度参数θ和可靠度函数R(x)的Bayes估计比MLE的值更精确,且MRE依次减小。2 极大似然估计和置信区间
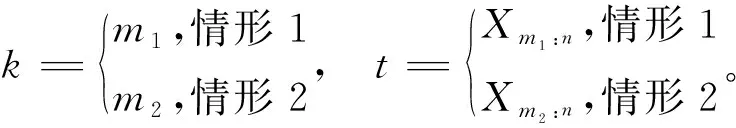
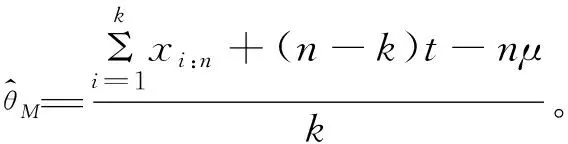
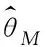
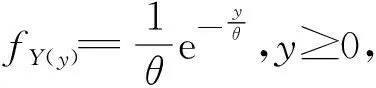

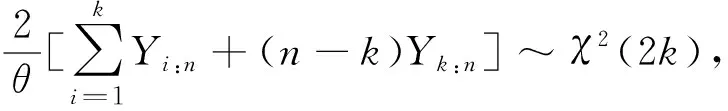
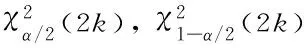
3 门限参数已知时的Bayes估计
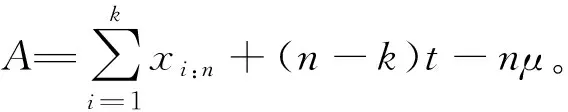
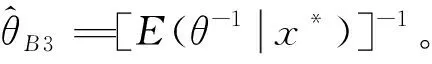
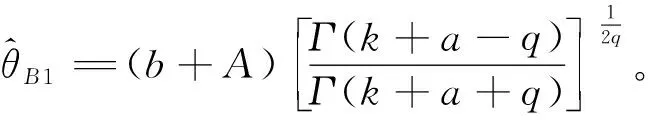

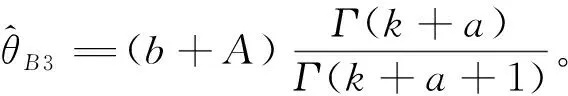
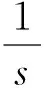
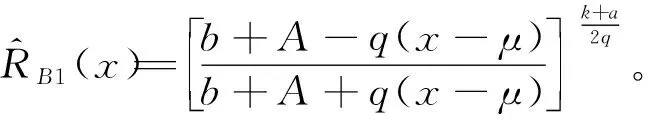
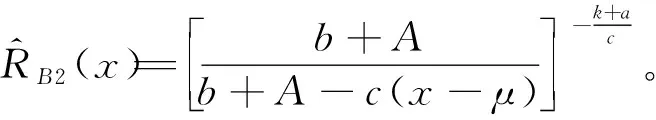
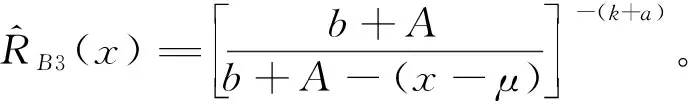
4 算例分析

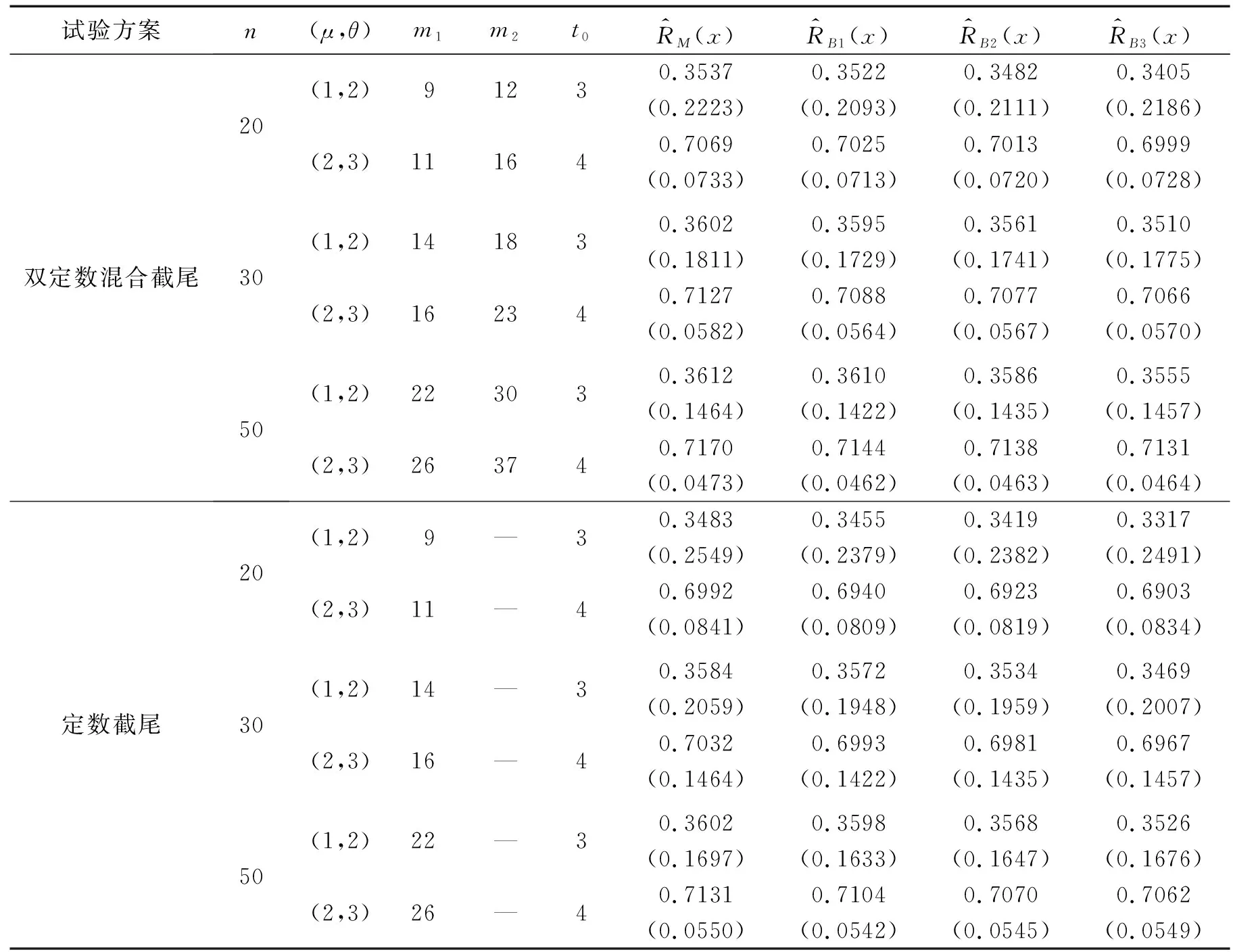
5 结 论

