一类带有临界指数的分数阶Schrödinger-Poisson系统正解的存在性

廖家锋,蒋 维

(西华师范大学 a.数学与信息学院,b.公共数学学院,四川 南充 637009)

考虑如下分数阶Schrödinger-Poisson系统

(1)

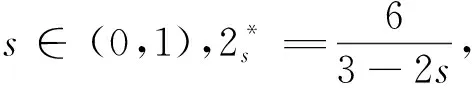
(-Δ)s代表s阶分数阶Laplacian算子,根据文献[1],定义如下:

其中P.V.代表柯西主值,C3,s是与s有关的维度常数。近年来,分数阶Laplacian方程被广泛研究和应用在金融和优化等许多领域中[2-4],因此引起了很多数学家对分数阶Schrödinger-Poisson系统的关注。

近年来,一些文章[5-10]研究了如下带有临界指数的分数阶Schrödinger-Poisson系统

(2)

定理1如果条件(V1)(V2)和(F1)—(F4)都成立,则系统(1)至少存在一个正解。

1 预备知识

本文所用到的符号有:

(3)

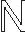
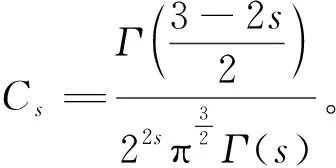
(4)

方程(4)对应的能量泛函I为

故,对于所有的v∈H,都有

此外,易知能量泛函I的临界点与方程(4)的解是一一对应的。

2 定理1的证明

1)对所有的u∈H,满足φu≥0;

引理2如果条件(V1)(F1)和(F2)成立,则

(a)存在ρ,α>0,当‖u‖=ρ时,满足I(u)≥α;

(b)存在e∈H,当‖e‖>ρ时,满足I(e)<0。

证明(a)根据条件(F1)和(F2)可知,对所有的ε>0,存在Cε>0,满足

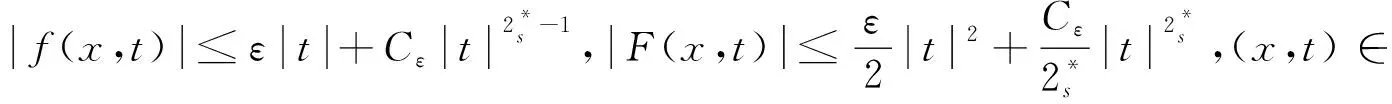
(5)

令Σρ={u∈H:‖u‖≤ρ},其中ρ>0,根据Sobolev不等式和(V1),可以推出

再根据引理1,对所有的u∈∂Σp,可以知道

由于ε足够小,故可以假设ε∈(0,V0),当ρ>0充分小时,可以推得

故(a)成立。

(b)对任意的t≥0,u∈H{0},有

于是,当t→+∞时,满足I(tu)→-∞。因此,存在t0>0充分大,满足‖t0u‖>ρ以及I(t0u)<0。取e=t0u∈H,则(b)也成立。从而,引理2证毕。

定义

(6)

其中

Γ={γ∈C([0,1],H):γ(0)=0,I(r(1))<0}。

利用山路定理,存在序列{un}⊂H,使得

I(un)→c>0,I′(un)→0。

证明若{un}是泛函I在H上的局部的(PS)c序列,则当n→∞时,满足

I(un)→c,I′(un)→0。

(7)

可以断言:{un}是H上的有界序列。事实上,当n足够大时,根据条件(F4)以及(7)式,有

这说明序列{un}在H上有界。故可知{un}存在子列(不妨仍记为{un})和u∈H,当n→∞时,满足

(8)

(9)

(10)

再结合(10)式,可以推出

(11)

(12)

让wn=un-u,根据Brézis-Lieb引理[13-14],有

‖un‖2=‖u‖2+‖wn‖2+on(1)。

(13)

根据Lebegue控制收敛定理和上式,可以知道

(14)

进一步,结合(13)式和(14)式,可知

(15)

同理,可得

(16)

(17)

(18)

(19)

证明由引理2知,当t>0足够小时,有I(tvε)>0;当t→∞时,有I(tvε)→-∞。又有I(0)=0,因此存在tmax>0,使得I(tmaxvε)=supt≥0I(tvε)>0。由于对所有的ε>0,都存在tε>0,满足‖tεvε‖=ρ,故由引理2知

0<α≤I(tεvε)≤I(tmaxvε)。

根据I的连续性,可以知道存在ε1>0和T1>0,使得对所有的ε∈(0,ε1),满足tε≥T1。再根据条件(F1)(F2)和(18)(19)式可知,存在正常数C1,C2和C3,使得当ε>0充分小时,满足

(20)

因此,存在ε2>0和T2>0,使得对所有的ε∈(0,ε2),有tε≤T2。此外,根据(20)式,可推得

(21)

定理1的证明根据引理2,可以得到泛函I具有山路几何结构。再结合引理3-4得到,存在序列{un}⊂H,满足I(un)→c,I′(un)→0,n→∞。从而序列{un}在H中有界且存在收敛子列(仍记为{un}),且存在u∈H,满足un→u(n→+∞)。再由山路引理(见文献[16],定理2.1),可以知道I(u)=c>0,I′(u)=0。因此,(u,φu)是系统(1)的一个非平凡解。又因为

所以有

≥‖u-‖2,