基于LAMOST和Gaia DR3探测银河系盘翘曲的进动
李 祥,杨 鹏,罗杨平
(西华师范大学 物理与天文学院,四川 南充 637009)
翘曲是许多盘星系中常见的非对称结构[1]。例如Ann和Park[2]观测了325个星系,发现其中的236个星系是翘曲的。作为一个典型的盘星系,银河系同样拥有一个翘曲的盘,从利用中性氢[3]作为示踪剂,至尘埃[4]、分子云[5]以及不同的恒星示踪天体[6],翘曲的形成机制一直在探索之中,而对于进动的研究将有助于对形成机制的理解。

前人研究工作中使用的观测数据样本,或者没有足够的自行测量,或者数据的精度不足。Gaia DR3[15]的最新数据提供了良好的契机去进行一些探索。红团簇星是氦核燃烧的水平分支星,距离测量准确,在加上精确的自行数据,可以促进对翘曲进动、扭矩的了解。本文将使用自行精度更高的Gaia DR3[15]和LAMOST DR5[16]红团簇星样本,基于Chrobáková和López-Corredoira[14]的翘曲模型,再次计算银河系盘翘曲的进动,对前人研究的部分结果进行检验。
1 数 据
1.1 数 据
本文使用的数据来自Ting等[17]提供的星表,包含175 202颗LAMOST[16]红团簇星样本,包括位置、自行、视向速度、距离等基本信息,其中距离的不确定度为10%。该星表被广泛用于探索恒星质量和年龄[18]。
1.2 样本筛选
通过与最新发布的Gaia DR3[15]巡天数据交叉匹配,使得样本拥有精度更高的自行,Gaia DR3[15]的自行不确定度在星等G<15 mag时,为0.02~0.03 mas·yr-1;而在星等G为17、20、21 mag时,分别为0.07、0.50、1.40 mas·yr-1。
选源标准参考 Chrobáková和López-Corredoira[14]及Wang等[7]的工作。为了选取外部银盘恒星(距离,金属丰度),且为确保恒星参数的准确度,考虑信噪比大于20和年龄小于15 Gyr,速度的选择标准也主要是为了关注盘星,尽量避免晕星污染。具体选择标准包括:
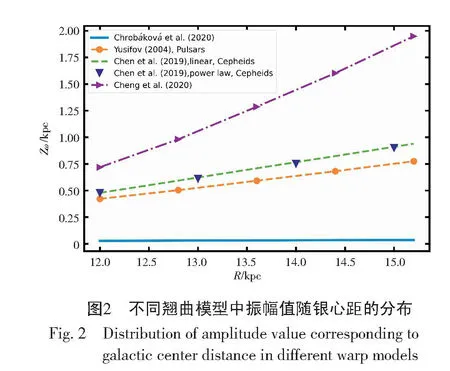
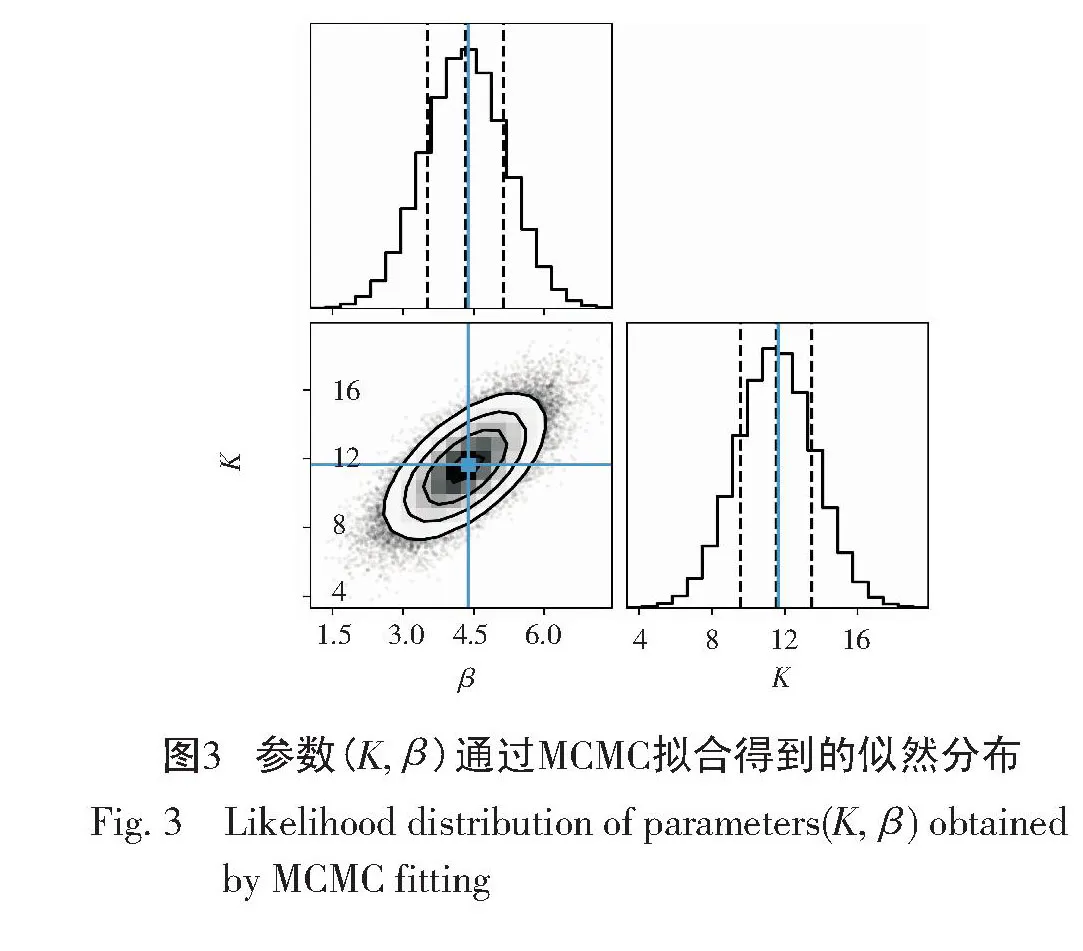
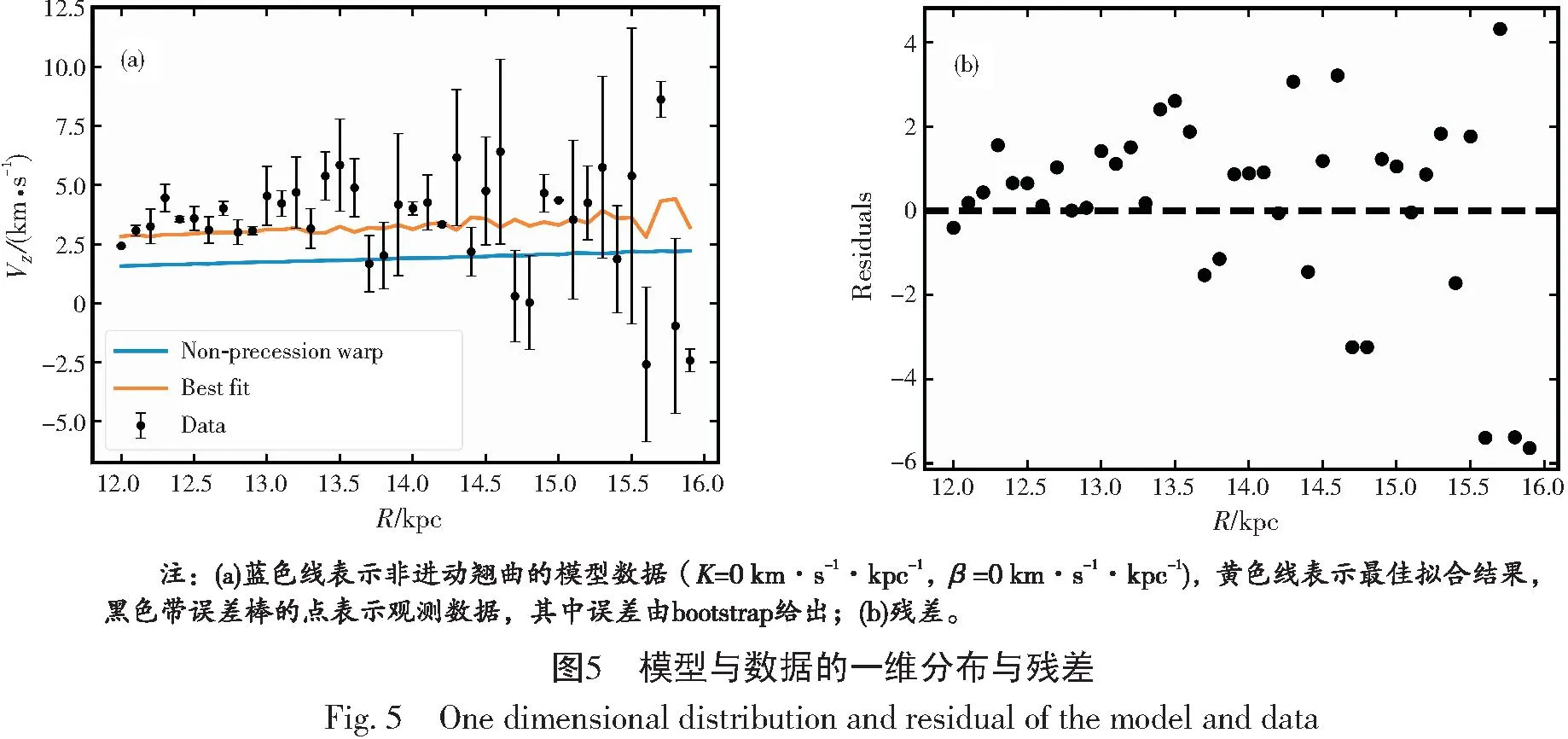
(1)12 kpc (2)S/N>20,Age<15 Gyr; (3)[Fe/H]>-1.3 dex; (4)3D velocities:VR=[-150,150] km·s-1,Vφ=[-50,350] km·s-1,VZ=[-150,150] km·s-1。 最终得到约23 000颗红团簇星样本,其R-φ/deg平面分布如图1所示。 本次工作中恒星的三维速度(VR,Vφ,VZ)基于Galpy[19]方法得出,其中太阳的位置为R⊙=8.34 kpc[20],Z⊙=27 pc[21],太阳的本征运动(U⊙,V⊙,W⊙)=(9.58,10.52,7.01) km·s-1[22],局域静止标准(LSR)绕银心的圆周运动速度ΩLSR=238 km·s-1[23]。除此之外,还依次计算了银心距(R)、垂直于银道面高度(Z)以及方位角(φ),这些运动学参数在Wang等[24-29]的工作中有详细描述。 本次工作使用的模型来自Chrobáková和López-Corredoira[14]的研究,该模型将翘曲合理地描述为一系列倾斜的环,在以银河系为中心的柱坐标系(R,φ,Z)中建模,其在银河系盘平面上的平均高度(Zω)为: Zω=CωRεωsin(φ-φω)+17, (1) 式中:以银心距R的εω次幂表示翘曲的倾斜程度,Cω为翘曲振幅,φω为节点线的方位角,17 pc项用于补偿太阳在平面上方的高度[30]。 最后模型中恒星的垂直速度表达式为: VZ(R,φ)=Cω,0RεωKsin(φ-φω,0)-Cω,0Rεωβcos(φ-φω,0)+Cω,0Rεω-1cos(φ-φω,0)Vφ, (2) 式中:Cω、εω、φω为自由参数,为了拟合数据,本次工作选择Chrobáková等[31]的结果: 使用马尔可夫链蒙特卡洛方法(MCMC)[32]获得最佳拟合值,得到收敛参数时,MCMC大小为50×2×10 000,步长为50。基于MCMC拟合的每个参数的最佳拟合值将在下一节中展示。 图2展示了4个不同翘曲模型的最大振幅值,其中Yusifov[33]的模型基于脉冲星,Chen等[34]的样本为造父变星,Cheng等[13]采用APOGEE样本,Chrobáková和López-Corredoira[14]的样本为 Gaia DR2[12]具有视向速度的红团簇星样本。值得注意的是,Poggio等[11]所用模型与Chen等[34]的一般形式相同。不同工作采用不同的样本和模型,从而导致高度变化的不同。从图2可以看出,Chrobáková和López-Corredoira[14]的模型中振动幅度也远小于Chen等[34]的模型,由此通过比较不同翘曲模型的翘曲进动值,发现振幅越大,进动越大,翘曲的进动与模型中振动幅度可能存在关联。 为了验证模型拟合的结果,将模型预测的垂直速度与观测数据进行比较。图4展示了通过模型参数(K,β)获得的模拟数据与观测数据在X-Y平面的分布,图4(a)为观测数据,图4(b)为采用非进动翘曲(Non-precession warp)模型,即模型中视进动为0(K=0 km·s-1·kpc-1,β=0 km·s-1·kpc-1)时给出的模拟数据,图4(c)为最佳拟合结果。从图4中可以看出,观测数据与最佳拟合结果所得模拟数据虽然有一点差异,但因为造成垂直运动的可能机制有很多,所以定性匹配是可以接受的。 一维分布如图5所示,图5(a)展示了垂直速度作为银心距的函数,图5(b)展示了残差。从图5中可以看出,最佳拟合结果能够匹配观测数据的总体趋势。 基于具有高精度自行的Gaia DR3和LAMOST红团簇星样本,并应用了一个基于Gaia DR2数据研究结果的翘曲模型对银河系盘翘曲的进动进行了量化分析。通过比较不同翘曲模型的翘曲进动值,发现翘曲的进动与模型中振动幅度可能存在关联。使用Chrobáková和López-Corredoira[14]的翘曲模型计算了翘曲的进动,得到翘曲进动的最佳拟合值β= 4.32 ± 0.8 km·s-1·kpc-1。本文是探索银河系盘翘曲的一部分工作,未来将进一步利用更精确的数据、更完备的模型,继续努力理解翘曲,期待未来会有更多的工作展示。2 模 型
3 结 果
3.1 进动与振幅可能存在关联
3.2 翘曲进动值的计算
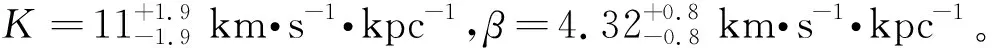

4 结 论

