一类与斜率有关的定点问题的“不联立”解法
湖北省大冶市第一中学 胡晓臻 (邮编:435100)
湖北省天门中学 李 苗 (邮编:431700)
在处理直线与圆锥曲线的位置关系问题中,通性通法是联立直线与圆锥曲线,转化为韦达定理表达题意,运算量往往很大,许多同学只是记住了这种算法的套路,并没有理解其中的道理.本文采用不联立的方法解决一类定点问题,旨在强调直线与圆锥曲线位置关系的表达方式不需要套路化,也可以等价转化为相应的知识点解决问题,以此培养学生的数学思维.
为了方便说明,先了解两个基本知识:


(2)经过平面上两点P(x1,y1),Q(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1).

图1
例1(2021年陕西汉中模拟预测)已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,y0)(y0>0)在抛物线C上,O为原点,且OF⊥MF,|MF|=2.
(1)求抛物线C的方程;
(2)若动直线l:x=my+t(m,t为参数)与抛物线C交于P(x1,y1),Q(x2,y2)两点,且直线MP的斜率与直线MQ的斜率之和为2,证明:直线PQ过定点.
解(1)y2=4x,M(1,2)

由题意得kMP+kMQ=2,则

两式相减得2(y2-y1)=y1x2-y2x1.
过两点P(x1,y1),Q(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1),对比可得直线恒过定点(-2,0).
说明本题题干中直接出现斜率和为定值,为了与过两点的直线方程一致,在代入条件的时候采用交叉代入化简,很快可以产生与过两点的直线方程一样的结构,就可快速找到定点.

(1)求E的方程;
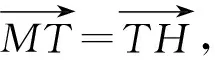




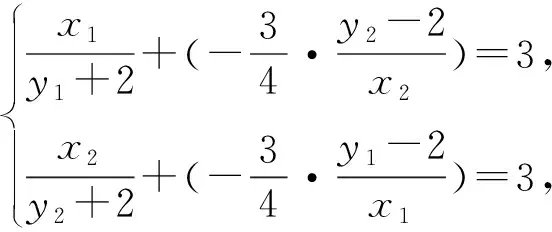
去分母得
两式相减得,y1x2-y2x1=-(y2-y1)-2(x1-x2),过两点M(x1,y1),N(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1),对比系数直线过定点(1,-2).
所以直线HN过定点A(0,-2)
图3

(1)求椭圆C的方程;
(2)点P在椭圆上,求线段BP的长度|BP|的最大值及取最大值时点P的坐标;
(3)不过点A的直线l交椭圆C于M,N两点,记直线l,AM,AN的斜率分别为k,k1,k2,若k(k1+k2)=1,证明:直线l过定点,并求出定点的坐标.



由k(k1+k2)=1得
两式作差得,k(x2-x1)+2(y2-y1)=y1x2-y2x1.过两点M(x1,y1),N(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1),对比系数得恒过点(-2,k).设l:y=kx+m代入得m=3k,所以y=kx+3k,所以直线l过定点(-3,0).
由上述几道题,我们可以归纳出解法的思路是:要证明一条直线过定点(x0,y0),就是要找到常数x0,y0,使得等式y1x2-y2x1=y0(x2-x1)-x0(y2-y1)成立,因此我们要设法构造出x1y2-x2y1的结构.在表达斜率的式子的时候,两直线的斜率如何多角度表达,交叉使用是解决问题的关键.本文希望通过几道定点问题讲清构造的思路,下面两道练习题,读者可尝试解决.
练习:
(1)求椭圆C的方程;

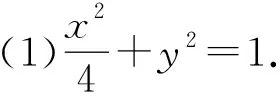



所以
两式相减得,2(y1-y2)-(x2-x1)=y1x2-y2x1,过两点M(x1,y1),N(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1),对比系数得恒过定点(2,-1).


图5
(1)求双曲线E的方程;
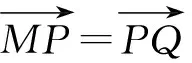

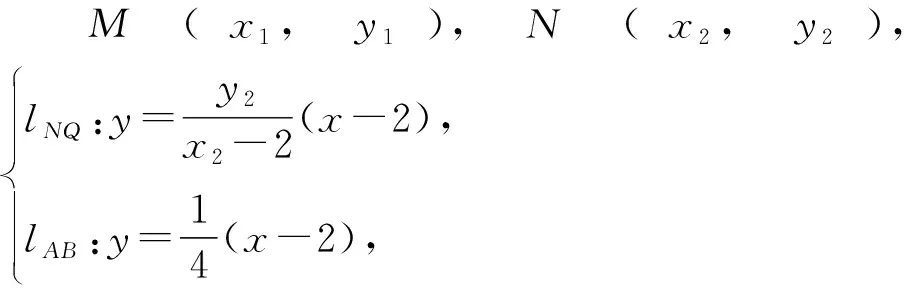
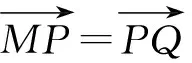
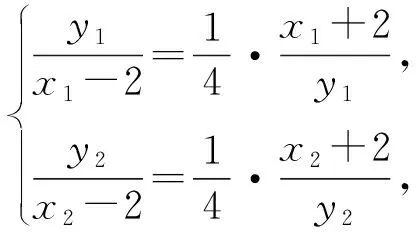
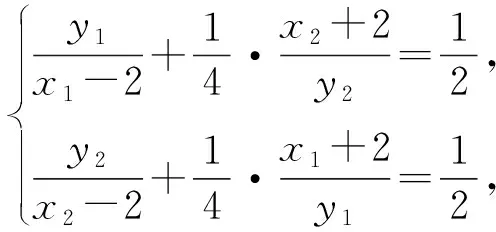
所以
两式相减得,2(x2-x1)-2(y2-y1)=y1x2-y2x1,过两点M(x1,y1),N(x2,y2)的直线方程是y1x2-y2x1=y(x2-x1)-x(y2-y1),对比系数得直线l过定点(2,2).

