新能源场站全工况下多逆变器并联驱动MGP的UPF控制

王强, 杨策, 郭伟, 林贺凯

(1.三峡大学 电气与新能源学院,湖北 宜昌 443002; 2.三峡大学 智慧能源技术湖北省工程研究中心,湖北 宜昌 443002)

0 引 言

随着大规模新能源对火电机组的逐渐替代,电网将呈现低惯量、高电力电子化等特点,这些特点,不利于电网的稳定运行[1-2]。而将同步电机对(motor-generator pair,MGP)技术用于间歇性新能源并网是近年来研究的一个方向,可以使新能源场站具备同步电机的优良属性,有利于电网的稳定运行[3]。主要体现在:新能源场站具备了真实的转动惯量、拥有了较强的惯性响应、增加了电网的频率支撑能力[4-5];同时在电网故障时,可以提供阻尼和无功功率支撑,加快电网电压的恢复[6-7],提高新能源场站的高、低电压穿越能力[8-9]。

考虑到在实际新能源并网系统中,单台逆变器容量有限,难以满足新能源场站的容量要求[10];同时设计单台大容量逆变器的难度较高、经济性较差,故新能源场站通常采用多逆变器并联的方式,来满足其并网容量要求[11]。同样,对于新能源场站中,用于驱动MGP的逆变器来说,也应采用并联的方式,来满足新能源场站的并网容量要求[12]。

文献[13]提出一种基于源网相位差的功率反馈控制方法,这种方法通过MGP输出功率的变化,来得到频率信号的微调量,从而实现逆变器对MGP的驱动,但这种方法中的频率信号只针对单台逆变器,不适用于多逆变器并联驱动MGP的场合。文献[14-15]通过对逆变器与同步电机的研究,提出逆变器并联驱动MGP的id=0矢量控制策略,该策略通过对各个逆变器q轴电流的控制,来实现多逆变并联驱动MGP。但在理论和仿真研究中,发现其存有一定的局限性,当MGP出力较大时,有可能会使得连接于MGP输入侧的逆变器输出功率因数过低,将导致难以保证MGP的有功传输效率;并且当前新能源场站多逆变器并联驱动MGP的研究,主要集中于等容量、同出力情况,其应用场景较为单一。

本文在逆变器电流环控制与同步电机单位功率因数(unity power factor,UPF)控制的基础上,提出多逆变器并联驱动MGP的UPF控制策略,该策略采用UPF计算MGP中同步电动机的定子d、q轴电流,并通过电流分配系数,将其分配到各台逆变器电流环控制当中,从而在多逆变器容量相等或不等、出力相同或不同的情况下,均可实现对MGP的驱动。为了更好地服务于工程实践,本文进行相关仿真研究,结果表明所提控制策略可以很好地保证新能源场站全工况下MGP的有功传输效率。

1 逆变器驱动MGP的工作原理

逆变器主电路如图1所示,其输出侧的回路控制方程为:

(1)

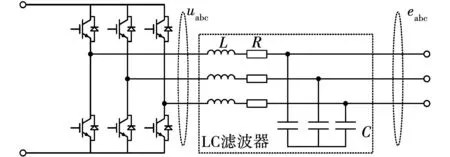
图1 逆变器主电路图

式中:ua、ub、uc为逆变器输出侧相电压;ea、eb、ec为滤波器输出侧相电压;ia、ib、ic为逆变器输出侧相电流;R、L为逆变器滤波电感的等效电阻和电感值。

为实现功率解耦,逆变器的并网控制通常采用dq坐标系,因此可将式(1)转变为:

(2)

式中:ud、uq为逆变器输出侧相电压的d、q轴分量;id、iq为逆变器输出侧相电流的d、q轴分量;ed、eq为滤波器输出侧相电压的d、q轴分量。

根据式(2)建立逆变器电流环控制,如图2所示,其中的控制参数均采用标幺值,通过对电流环进行两相同步旋转坐标系的解耦,从而得到dq轴坐标下的电压参考值,进而实现逆变器输出功率的解耦控制。

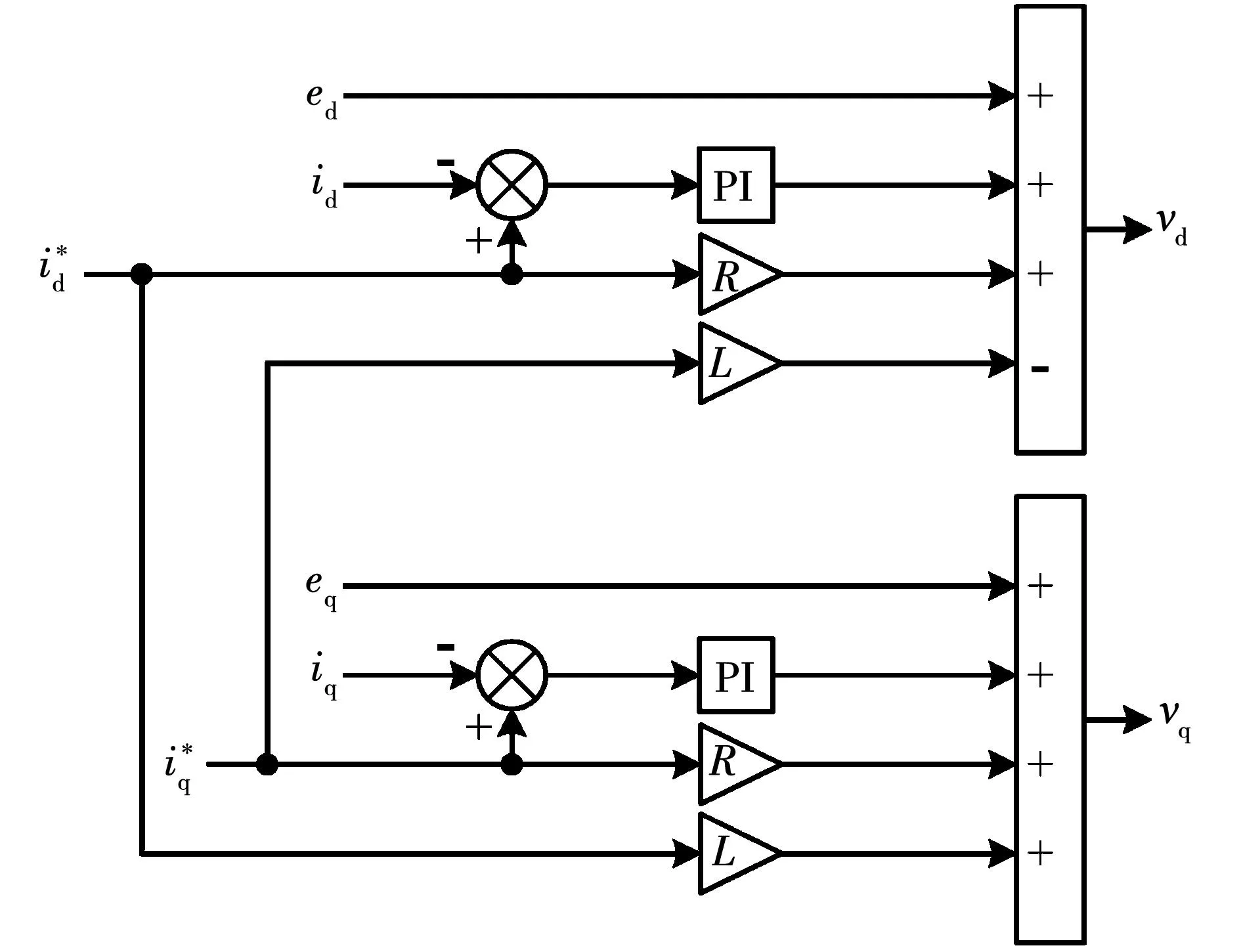
图2 逆变器电流环控制

MGP系统位于逆变器与电网之间,由一台同步电动机和一台同步发电机同轴连接构成。由于MGP中两台电机的电磁转矩耦合,因此,当调节电动机电枢电流使得电磁转矩增大时,就会使得MGP的功角增大,而功角的增大,将会使MGP的传输功率增加[14]。

dq坐标系下同步电机的转矩表达式[16]为

Te=1.5np(ψsdisq-ψsqisd)。

(3)

式中:np为同步电动机的极对数;ψsd、ψsq为同步电动机定子磁链的d、q轴分量;isd、isq为同步电动机定子电流的d、q轴分量。

结合逆变器电流环控制和式(3)可知,当多逆变器并联驱动MGP时,可通过各个逆变器的电流环控制,来改变MGP中电动机定子d、q轴电流的大小,从而实现电动机电磁转矩的调节,达到控制MGP功率传输的目的。

2 MGP中id=0矢量控制下逆变器输出功率因数分析

由第1节分析可知,多逆变器并联驱动MGP的核心,在于同步电动机定子d、q轴电流的控制。而当前常采用多逆变器并联驱动MGP的id=0矢量控制策略,其控制如图3所示,图中参数均为标幺值,且n台逆变器的额定容量相等、MGP与新能源场站额定容量之比为m。该策略将MGP中同步电动机的定子d轴电流置0,通过控制同步电动机定子q轴电流来实现电磁转矩的调节,从而达到控制MGP功率传输的目的。

图3 多逆变器并联驱动MGP的id=0矢量控制策略

同步电动机d、q轴电压、磁链方程[17]为:

(4)

(5)

式中:usd、usq为同步电动机定子电压的d、q轴分量;if为励磁电流;iDd、iDq为阻尼绕组中电流的d、q轴分量;Rs为定子等效电阻;Ld、Lq为定子绕组的d、q轴等效电感;Lmd、Lmq为d、q轴电枢感应电感。

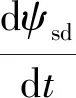
(6)

式中ψ=Lmdif,为励磁电流在d轴电枢感应电感上产生的磁链。

根据式(3)与磁链方程(5)可以得出

(7)

为了解当同步电动机定子电流变化时,磁链ψ的变化情况,从而分析同步电机的功率因数,将磁链ψ对定子q轴电流isq求导,可得

(8)

由式(8)可知,当同步电动机的定子q轴电流增大时,其磁链ψ将所随之减少。

当同步电机定子电流的d轴分量为0时,其功率因数角可以表示为

(9)

同步电机的功率因数为

(10)

在id=0矢量控制模式下,同步电动机出力增大时,其负载转矩增大,定子电流的q轴分量增大,由式(8)可知,磁链ψ减小,此时由式(9)和式(10)可知,电机的功率因数角增大,功率因数减小。若忽略MGP中的功率损耗,则MGP中同步电动机输出的有功功率与同步发电机发出的有功功率相等。也就是说,在id=0矢量控制模式下,MGP的出力较大时,有可能会使得连接于MGP输入侧的逆变器输出功率因数过低,将导致难以保证MGP的有功传输效率。

3 多逆变器并联驱动MGP的UPF控制

同步电动机的单位功率因数(UPF)控制可以使得同步电动机的功率因数达到接近或等于1的效果。因此,同步电动机定子d、q轴电流的控制可以采用UPF来计算,从而使得多逆变器并联驱动MGP时,尽可能多的输出有功功率。

同步电动机定子电流方向,按惯例,输入方向为正,但考虑到MATLAB/Simulink中同步电机模型中的定子电流是以输出电流作为正方向。因而,在通过单位功率因数(UPF)来求解定子d、q轴电流时,同步电动机定子电流应以输出电流作为电流正方向,此时同步电动机的电压、磁链方程如下:

(11)

(12)

结合式(3)和式(12),dq坐标系下同步电动机的转矩表达式可以写成:

Te=1.5np[ψisq-(Ld-Lq)isdisq]。

(13)

由于同步电动机转矩标幺表达式中无1.5np项,故磁链ψ的标幺表达式为

(14)

当同步电动机满足单位功率因数条件时,其定子电压、电流的矢量同相,即

(15)

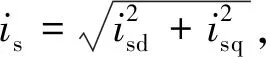
(16)

根据式(16),去掉超过电流最大值的解,isd可以用is表示为

(17)

同步电机定子q轴电流isq可表示为

(18)

同步电机的UPF控制的核心就是通过式(14)、式(17)、式(18)计算同步电动机定子d、q轴电流的参考值,从而保证同步电动机的功率因数接近或等于1。

多元三次方程求解较为复杂,但若能直接采集同步电动机定子d、q轴电流计算磁链ψ,将磁链ψ当作已知量,则同步电动机定子d、q轴参考电流可直接计算得出,这将会大大降低计算难度。

假设可以直接采集同步电动机定子d、q轴电流来计算磁链ψ。由式(14)、式(18)可知,磁链ψ对直接采集定子d轴电流isd的导函数为

(19)

式中:同步电动机定子以输出电流作为电流正方向,故其电磁转矩Te为负值,并且单位功率因数控制时,其定子d轴电流isd为正值,定子q轴电流isq为负值。

(20)

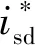
在上述分析的基础之上,结合逆变器电流环控制与同步电动机UPF控制,可以得到如图4所示的多逆变器并联驱动MGP的UPF控制策略,控制策略中的参数均采用标幺值,其中ki为第i个逆变器的电流分配系数,由于同步电动机定子电流以输出方向为正方向,与逆变器输出电流方向相反,故ki为负值。

图4 多逆变器并联驱动MGP的UPF控制策略

当等容量、同出力多逆变器并联,且MGP与新能源场站额定容量相同时,其电流分配系数ki为

ki=-1。

(21)

但等容量、同出力多逆变器并联,仅适用于单一的光伏电站或风电场,且该新能源场站中的光照强度或风速需默认相同。

为使多逆变器并联适用于多台逆变器容量相等或不等、出力相同或不同的全工况情况,本文基于逆变器电流标幺值、逆变器额定容量之比、MGP与新能源场站额定容量之比,得到每台逆变器的电流分配系数,即每台逆变器实际电流与n台逆变器实际电流总和的比,即

(22)

式中:ii为第i个逆变器的电流参考值,是以第i个逆变器额定容量为基准值,所得到的标幺值;多个逆变器额定容量之比为n1∶n2∶n3∶…∶nn;m是MGP与新能源场站额定容量之比。

此时多逆变器并联,不仅适用于单一的光伏电站或风电场,还适用于既含有风电又含有光伏的新能源场站;不仅适用于光照强度、风速等环境因素完全相同的新能源场站,还适用于光照强度、风速等环境因素存在差异的新能源场站;不仅适用于集中式新能源场站驱动MGP的场合,还适用于分布式新能源场站联合驱动MGP的场合。

4 仿真分析

图5为3台逆变器并联驱动MGP的原理图,仿真过程中,新能源场站的总额定容量设为60 MVA,直流电源电压都设为500 V,MGP中同步电机的额定电压为4 000 V,其他参数见表1 仿真参数。

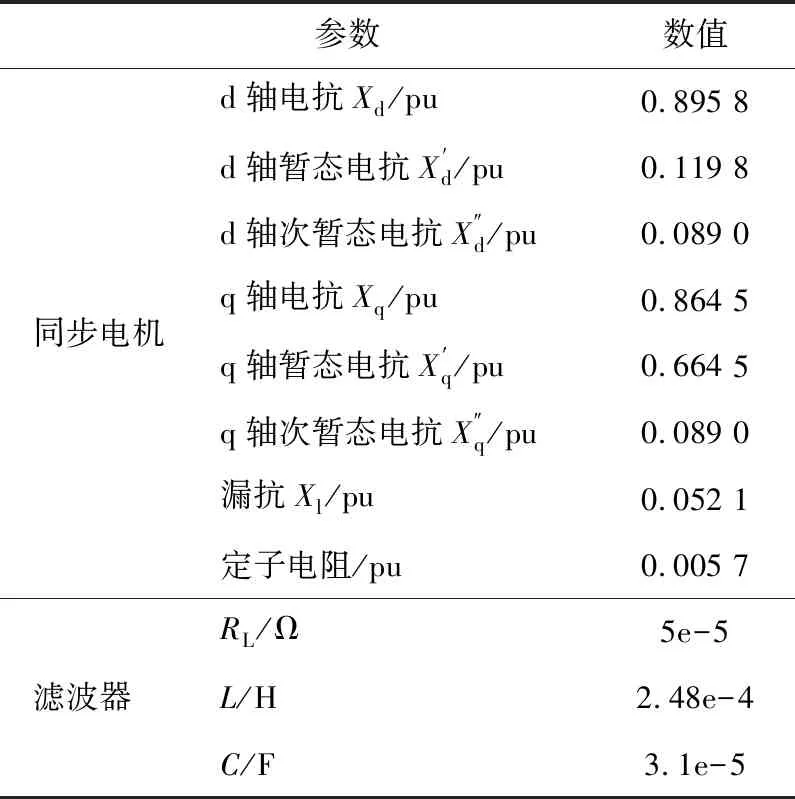
表1 仿真参数

图5 三台逆变器并联驱动MGP的原理图

4.1 MGP的id矢量控制策略仿真分析

4.1.1id=0矢量控制模式

进行id=0矢量控制模式下,多逆变器并联驱动MGP的研究,设置MGP的额定容量等于新能源的额定容量,且3台逆变器的出力保持相同。通过设定逆变器电流参考值i*分别为1、0.9、0.8、…、0.2、0.1来模拟新能源的不同出力,其仿真结果见表2id=0模式下逆变器输出侧功率因数,表中P、Q、S和cosφ分别为逆变器输出侧有功功率、无功功率、视在功率和功率因数。

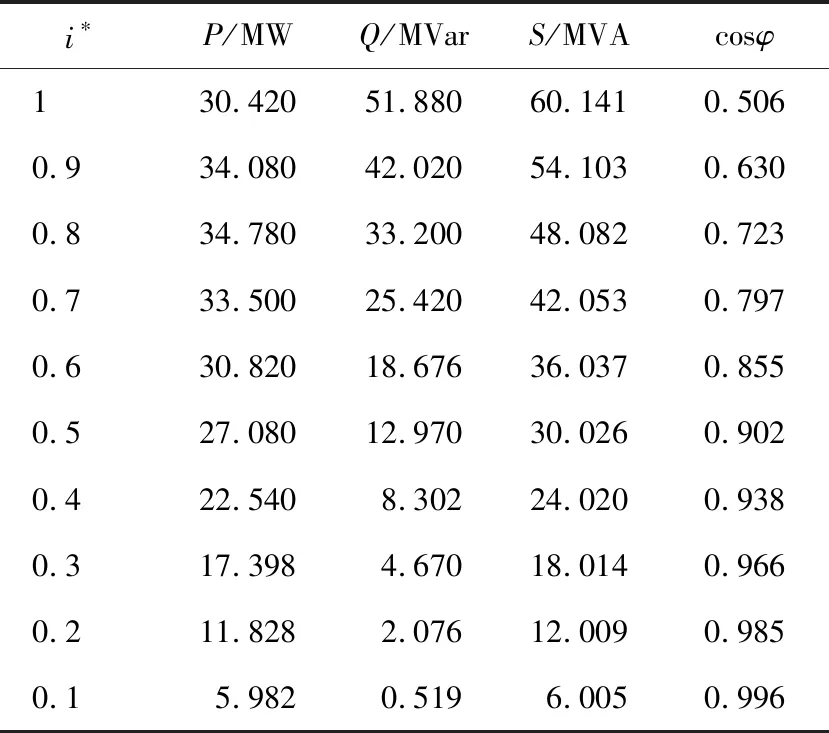
表2 id=0模式下逆变器输出侧功率因数

新能源场站额定容量与MGP的额定容量相同时,两者出力情况几乎一致,若忽略逆变器与MGP中的功率损耗,可认为新能源经逆变器并联驱动MGP并网的有功传输效率与逆变器输出侧功率因数在数值上相等。

由表2可知,当新能源与MGP出力在20%以下,MGP轻载运行时,逆变器输出侧功率因数接近于1,可保证新能源经逆变器并联驱动MGP并网的有功传输效率。然而,当新能源与MGP的出力增加时,逆变器输出侧功率因数随之越低,甚至当新能源额定容量运行时,其功率因数只能达到0.506,无法保证新能源通过MGP并网有功传输效率。

设置MGP与新能源场站的额定容量之比为m,分别在m取1、2、4、6的情况下进行上述仿真,其仿真结果见图6,该图是id=0矢量控制模式下逆变器输出侧功率因数。

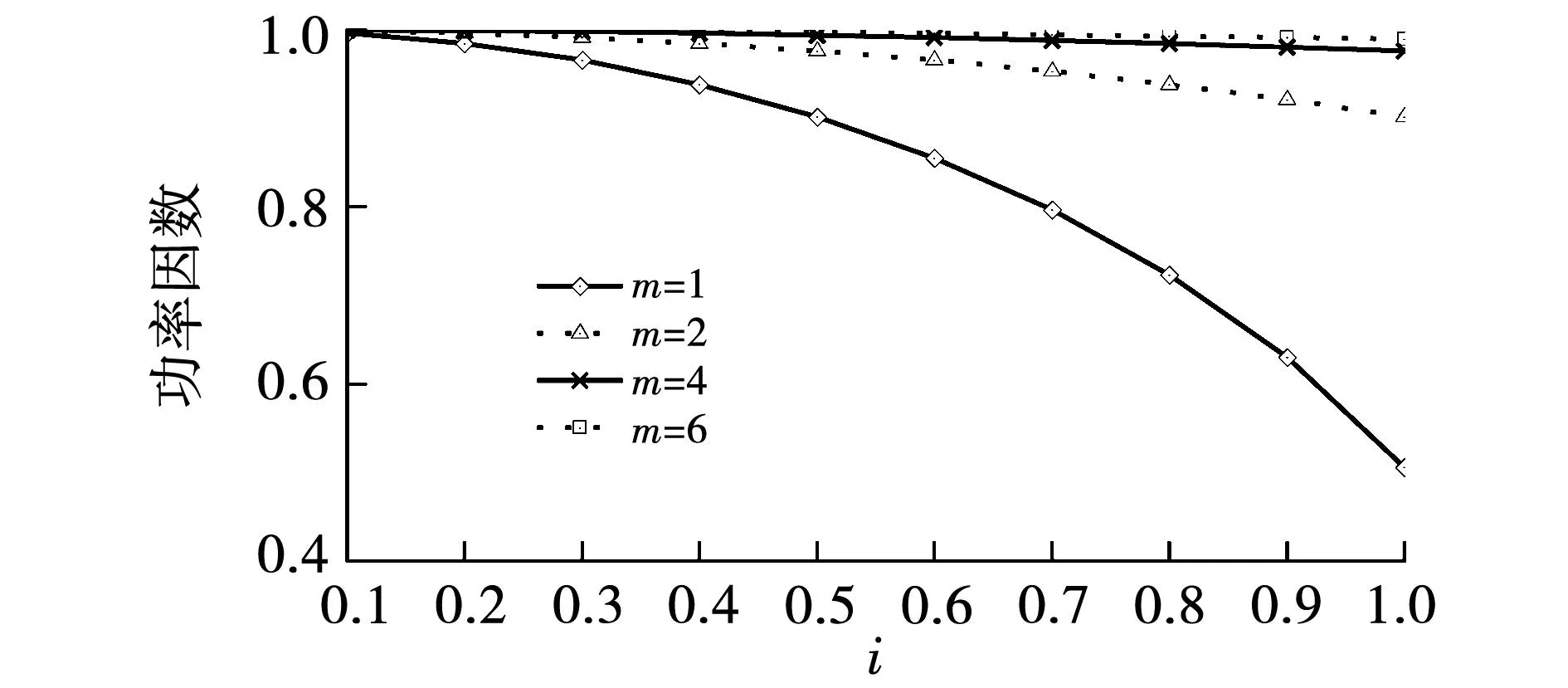
图6 id=0矢量控制模式下逆变器输出侧功率因数

由图6可知,新能源出力相同时,m越大,MGP的出力越低,逆变器侧功率因数越高;m相同时,新能源出力越大,MGP的出力就越高,逆变器功率因数越低。在m为1、2、4、6时,逆变器侧功率因数的最小值分别为0.506、0.902、0.976、0.990。若要让逆变器输出侧功率因数接近1,从而使得新能源通过MGP并网的有功传输效率尽可能高,则应控制MGP的额定容量是新能源额定容量的6倍左右。

在多逆变器并联驱动MGP的id=0矢量控制策略下,若MGP的额定容量与新能源额定容量相等,则在MGP出力较大时,无法保证新能源通过MGP并网的有功传输效率;若使MGP的额定容量是新能源额定容量的6倍左右,来保证MGP的有功传输效率,则MGP容量的提升不仅会增大投资成本,还会对MGP的容量使用造成严重浪费,并且MGP中同步电机的长期轻载运行还会影响其使用寿命,严重时,还会造成同步电机故障。

4.1.2id给定矢量控制模式

当前,多逆变器并联驱动MGP有id=0矢量控制模式和id给定矢量控制模式,常采用id=0矢量控制模式[14-15]。前文对id=0矢量控制模式进行了理论和仿真分析,分析了这种方法所存在的一些问题。为进一步研究,本节主要对id给定矢量控制模式进行仿真验证。

进行id给定矢量模式下,3台逆变器并联驱动MGP的研究,在仿真过程中,设定MGP的额定容量与新能源额定容量相同,且3台逆变器的出力保持相同。根据文献[13]的功率反馈控制方法,可以得到新能源与MGP额定运行时,MGP中同步电动机的定子d轴电流id为0.655。保持id=0.655不变,设定逆变器电流参考值i*分别为1、0.9、0.8、…、0.2、0.1来模拟新能源的不同出力,仿真结果见表3id=0.655模式下逆变器输出侧功率因数。

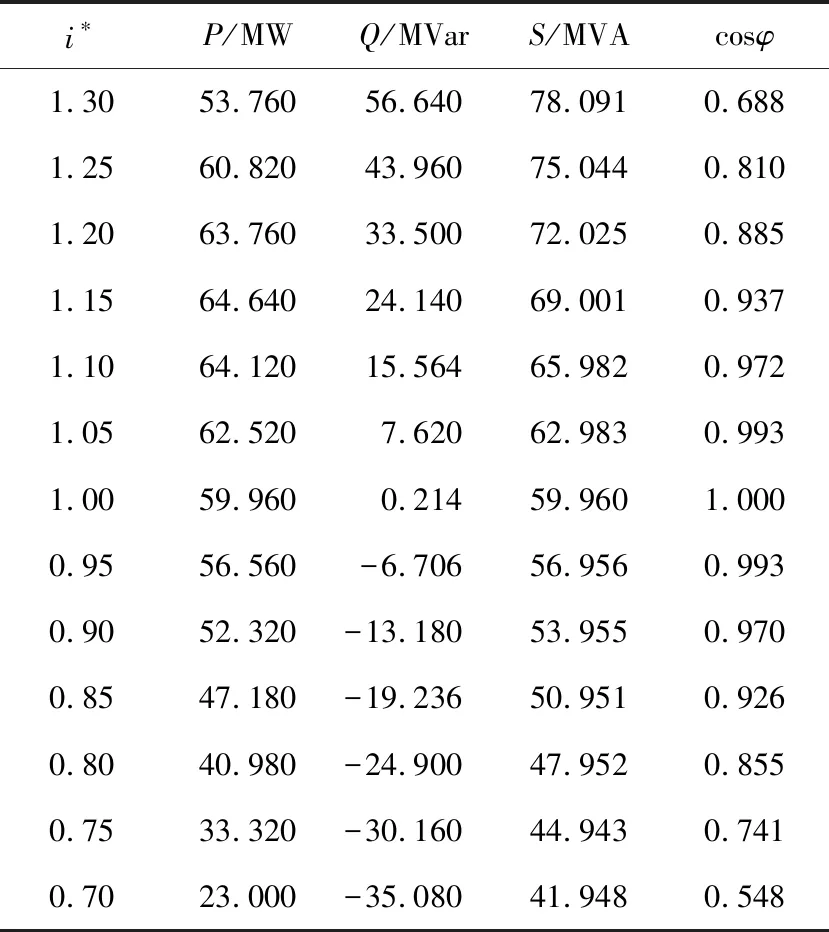
表3 id=0.655模式下逆变器输出侧功率因数

由表3可知,MGP与新能源额定运行时,逆变器输出侧功率因数为1.000,而随着新能源与MGP出力变化的增加,逆变器输出侧的功率因数在不断降低,并且下降趋势也越加明显。当新能源与MGP的出力变化在10%以内时,逆变器输出侧的功率因数可以达到0.970以上,可以较为有效地保证新能源通过MGP并网的有功传输效率;而当新能源与MGP的出力变化达到30%后,逆变器输出侧的功率因数降低至了0.548,此时,已无法保证MPG的有功传输效率。

与id=0矢量控制模式不同,在采用id给定矢量控制模式下,当新能源与MGP在额定出力时,逆变器输出侧的功率因数约等于1,足以保证新能源通过MGP并网的有功传输效率;且当新能源与MGP出力在额定出力附近,即出力变动不大时,也可以有效地保证新能源通过MGP并网的有功传输效率;但当新能源与MGP出力远离其额定出力,即出力变动较大时,难以保证MGP的有功传输效率。考虑到实际中,新能源出力通常具备间隙性和随机性的特点,故id给定矢量控制模式很难保证新能源通过MGP并网的有功传输效率。

4.2 MGP的UPF控制策略仿真分析

为了更好地使MGP系统在新能源场站中的应用,服务于工程实践,本节对UPF控制模式进行了三逆变器并联驱动MGP的仿真研究。仿真过程中,设置MGP的额定容量等于新能源额定容量,且3台逆变器的出力保持相同。设定逆变器电流的参考值i*分别为1、0.9、0.8、…、0.2、0.1来模拟新能源的不同出力,仿真结果见表4 UPF模式下逆变器输出侧功率因数。

表4 UPF模式下逆变器输出侧功率因数

由表4可知,虽然UPF控制模式下,新能源与MGP的出力增大时,逆变器输出侧的功率因数仍呈现出下降的趋势,但下降趋势却极不明显。当新能源与MGP出力10%时,逆变器输出侧功率因数可达到0.999 98,而当新能源与MGP在额定出力时,逆变器器输出侧功率因数最小,但仍可达到0.998 38,两者只差0.001 60,可见新能源与MGP的出力大小对逆变器输出侧功率因数的影响几乎为0。

设置MGP与新能源场站的额定容量之比为m,分别在m取1、2、4、6的情况下进行上述仿真,其仿真结果见图7 UPF控制模式下逆变器输出侧功率因数。

图7 UPF控制模式下逆变器输出侧功率因数

由图7可知,在m为1、2、4、6时,逆变器输出侧功率因数在新能源额定出力下,达到最小值,分别为0.998 38、0.999 59、0.999 90、0.999 96。由此可知,新能源出力相同下,尽管m越大,MGP出力越低,逆变器输出侧功率因数越大,但逆变器输出侧功率因数最大值与最小值的差为0.001 58,微乎其微。故UPF控制模式下,增大MGP的额定容量,虽然也可以增加逆变器输出的功率因数,提高新能源通过MGP并网的有功传输效率,但提高有限,近似于0。并且考虑到MGP额定容量等于新能源额定容量时,就可以使得逆变器输出侧功率因数达到0.998以上,足以保证新能源通过MGP并网的有功传输效率,因此,无需额外花费成本增大MGP的额定容量。

在UPF控制模式下,逆变器并联侧输出功率因数只能达到0.998,接近于1,其难以达到1的主要原因为:在同步电动机定子电流计算过程中,忽略了同步电动机定子等效电阻及电流参数动态变化的影响;在逆变器电流环控制当中,忽略了滤波器中电容支路的电流,默认了逆变器输出总电流为同步电动机定子流入电流。

4.3 UPF控制模式

4.3.1 等容量多逆变器并联驱动MGP的仿真分析

设置3台逆变器的电流参考值为i1、i2、i3,MGP的电流参考值为is,3台逆变器的额定容量之比n1∶n2∶n3为1∶1∶1。仿真初始时刻,设置i1、i2、i3均为1;在10 s时,将i1、i2、i3均减小到0.8,来模拟等容量、同出力情况;在15 s时,将i1减小到0.6、i2减小到0.7、i3保持不变,来模拟等容量、不同出力情况。仿真结果见图8 等容量下各台逆变器有功输出、图9等容量下MGP与逆变器输出有功和表5 等容量下MGP与逆变器输出有功。表5中:P1、P2、P3分别为逆变器1、2、3输出的有功功率;P123为3台逆变器总输出有功功率;PMGP为MGP输出有功功率。

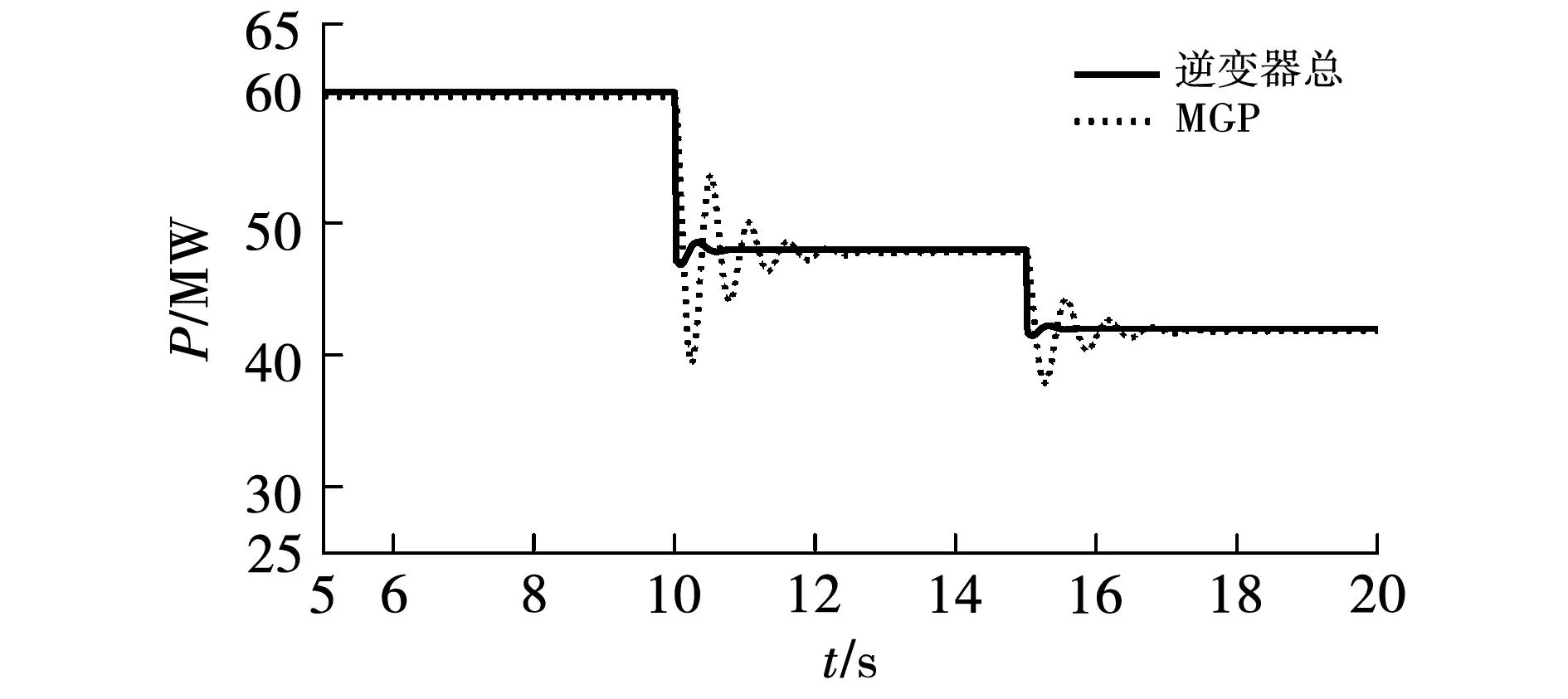
图9 等容量下MGP与逆变器输出有功

由图8可知,等容量下,在第10 s逆变器电流指令变化相同时,3台逆变器出力情况相同,可快速响应电流指令变化;在第15 s逆变器指令变化不同时,3台逆变器出力情况不同,分别跟随其自身电流指令变化。

由图9可知,等容量下,不管是同出力还是非同出力,MGP输出的有功功率总是跟随逆变器总输出的有功功率,且当新能源场站出力发生变化时,逆变器的暂态过程不超过0.5 s,MGP的暂态过程不超过3 s。

将图8与图9中的有功功率数据进行汇总,得到表5,由此可知,等容量下,无论是同出力还是不同出力,各逆变器与MGP输出的有功功率基本上与其自身的电流指令成正比。

4.3.2 非等容量多逆变器并联驱动MGP的仿真分析

设置3台逆变器的额定容量之比n1∶n2∶n3为3∶2∶1。仿真初始时刻,设置i1、i2、i3均为1;在10 s时,将i1、i2、i3均减小到0.8,来模拟非等容量、同出力情况;在15 s时,将i1减小到0.6、i2减小到0.7、i3保持不变,来模拟非等容量、不同出力情况。仿真结果见图10非等容量下各台逆变器输出有功、图11非等容量下MGP与逆变器输出有功和表6非等容量下MGP与逆变器输出有功。

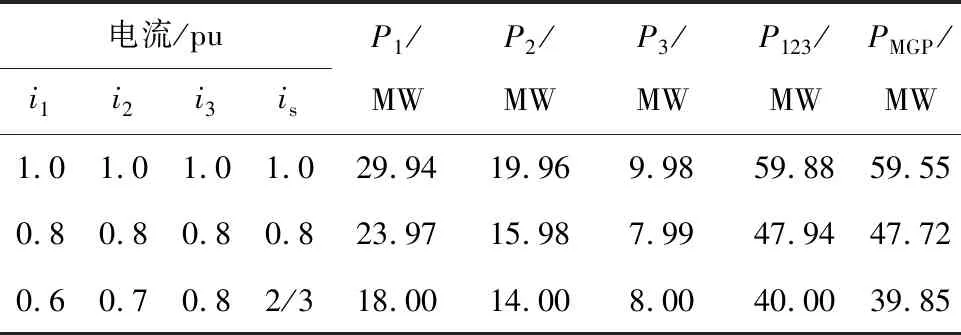
表6 非等容量下MGP与逆变器输出有功

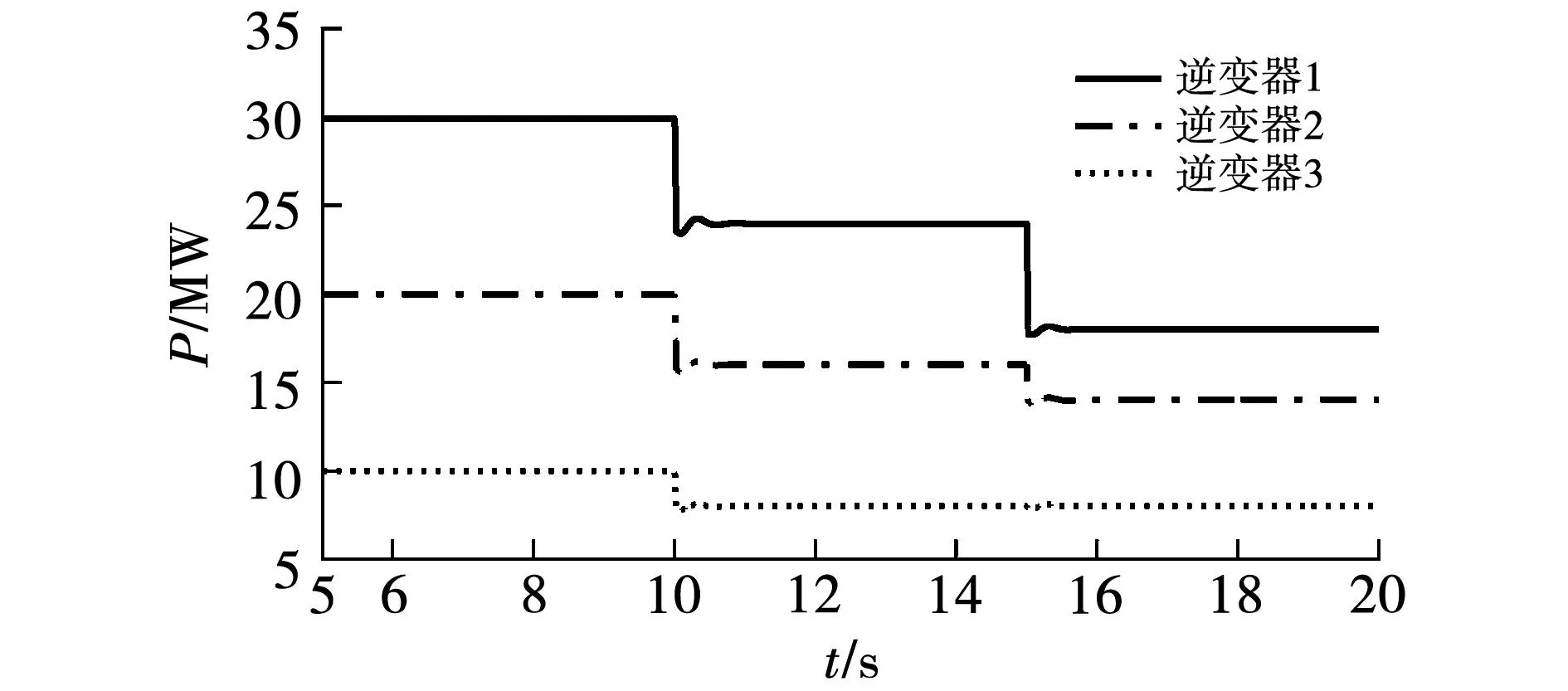
图10 非等容量下各台逆变器输出有功

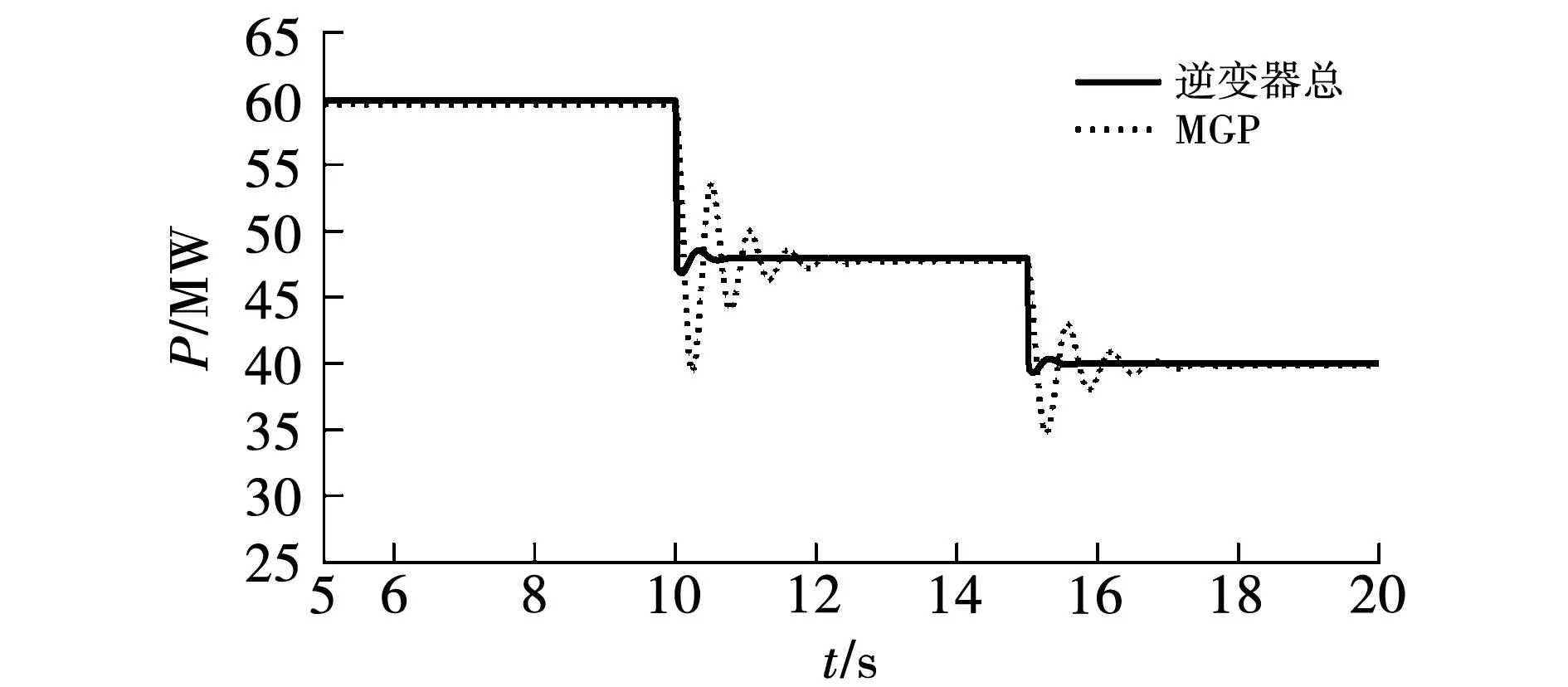
图11 非等容量下MGP与逆变器输出有功

由图10可知,非等容量下,无论出力相同还是不同,3台逆变器的出力都分别跟随各自电流指令的变化而变化。

由图11可知,非等容量下,不管是同出力还是非同出力,MGP输出的有功功率总是跟随着逆变器总输出的有功功率,且MGP输出有功的大小略低于逆变器总输出的有功。在第10、15 s时,新能源场站的3台逆变器出力发生较大变化,导致MGP的输入功率也随之改变,给MGP中的同步电机带来大干扰,发生了暂态过程,因此MGP的输出功率发生了减幅振荡过程,但由于同步电机的优良属性,振荡时间较短,不足3 s。

将图10与图11中的有功功率数据进行汇总,得到表6,由此可知,非等容量下,无论是同出力还是不同出力,各逆变器与MGP输出的有功功率基本上与其自身的电流指令成正比。

在多逆变器并联驱动MGP的UPF控制中,电流分配系数ki的存在,使得多逆变器在容量相等或不等、出力相同或不同的情况下,都可以很好地保证各台逆变器与MGP的功率输出。

5 结 论

本文分析了id=0和id给定矢量控制模式下,多逆变器并联驱动MGP有功传输效率的局限性,并结合工程实际,提出了多逆变器并联驱动MGP的UPF控制策略。经理论分析与仿真验证,可得出以下几点结论:

1)id=0矢量控制模式在MGP出力较大时,以及id给定矢量控制模式在MGP出力变动较大时,都会导致逆变器输出功率因数减小、难以保证新能源通过MGP并网的有功传输效率。

2)采用多逆变器并联驱动MGP的UPF控制策略,逆变器输出侧功率因数都在0.998以上,为新能源通过MGP并网的有功传输效率提供了保证。另外,利用磁链ψ与同步电动机定子d轴电流具备负反馈的特性,将计算过程可从多元三次方程求解降为直接求解,并采用调整逆变器电流分配系数ki的措施,实现了逆变器与MGP输出的有功功率相互匹配,可很好的适应全工况场景、吻合工程的实际应用需求。