具有低输出纹波的双电感复用无桥buck-boost PFC变换器
陈正格, 许建平, 陈旭, 漆谨
(西南交通大学 电气工程学院,四川 成都 611756)
0 引 言
在全球范围内,照明系统消耗了近20%的电力,预计未来20年照明能源需求将进一步增加[1]。近十年来,传统光源正被寿命更长、发光效率更高的发光二极管(light emitting diode,LED)取代[1-2]。目前,LED照明被广泛应用于城市亮化工程、无人机表演、路灯照明、大型场馆照明、电动汽车、农业等多种场合[3]。随着LED的大范围使用,Energy star等产品性能标识对LED的要求也变得苛刻。如2009年生效的标准中,仅要求功率≥ 25 W的民用LED照明功率因数(power factor,PF)≥0.7,商用LED照明PF≥0.9;而2011年生效的标准已对功率≥5 W的LED照明均做出上述要求[4]。因此,研究高性能的LED驱动具有超前意义。
目前,LED驱动主要性能指标包括成本、使用寿命、效率、光谱调节能力、光照范围等[4-5]。由于应用场合的差异,LED驱动电路的性能侧重点有所不同。比如,在街边路灯照明中,由于数量众多的路灯整体能耗大、维护成本高,LED装置的使用寿命、光照范围与发光效能较为重要[6-7];而在农业应用中,由于植物在不同生长阶段对不同特定波长光源有不同的反应,因此LED装置应具备精细可控的光谱调节能力、低启动电流与高效率等特性[8]。
因此,为应对特定场景的不同要求,相关学者提出不同的功率因数校正变换(power factor correction,PFC)电路驱动LED。为延长AC-DC驱动电路的使用寿命,学者们提出多种输出电流纹波抑制、消除电路,避免在输出侧使用寿命有限的电解电容[9-12]。在液晶显示器中,为实现LED高演色性(color rendering index,CRI),避免传统白光LED色移现象[13],学者们采用多路并联RGB-LED[14]、可快速调节母线电压的辅助电路[15]、母线电容可控投切[16]等方式;其次,为实现多路输出LED串的均流,简单、高效、低成本的多种无源均流电路被学者提出与分析[17-19]。
另外,为降低电价增长带来的变换器运行成本,同时响应低碳的政策号召,各类无桥AC-DC变换器被提出[20-29]。这类拓扑不再使用二极管整流桥,而是通过减少电流通路中半导体器件数量实现更低的导通损耗[20]。近十年来,基于boost、Cuk、buck-boost等广泛应用于AC-DC LED驱动的经典电路拓扑,学者们提出更高效的无桥AC-DC LED驱动变换器[24-27]。文献[24]提出基于双并联Cuk变换单元所得的无桥Cuk电路并分析其工作特性。文献[25]提出谐振无桥boost LED驱动电路,通过谐振电容均流网络实现多路均流。文献[26]基于传统boost PFC与半桥LLC谐振电路的两级架构,提出一种通过器件融合的准单级无桥电路,其具有更少的开关器件。文献[27]基于双buck-boost变换单元给出一种低开关管应力的单级无桥buck-boost PFC拓扑,但该类无桥拓扑的双变换单元仅交替工作于半个工频周期,器件利用率不高。
针对文献[27]的缺点,本文提出一种通过双电感复用实现低输出电流纹波的无桥buck-boost PFC变换器。所提出的变换器具有以下特性:1)其中一个电感与输入侧连接,工作于电流断续导电模式(discontinuous conduction mode,DCM),变换器可采用单闭环控制实现高PF与输出调节;2)另一电感与输出侧连接,工作于电流连续导电模式(continuous conduction mode,CCM),滤除更多高次输出谐波,实现低输出纹波;3)类似传统buck-boost PFC变换器,该改进型拓扑仍然可以使用含谐波注入的控制进一步降低输出电流纹波。
本文分析变换器工作原理,推导PF值、输出纹波io,rip表达式,给出谐波注入的控制方法。最后,通过实验验证拓扑的可行性与理论分析的正确性。
1 无桥buck-boost PFC变换器
1.1 提出的拓扑介绍
由于buck-boost PFC变换器的功率通常仅为数十瓦,一般采用简单的单电流闭环控制。图1给出了传统buck-boost PFC变换器主电路图,包括二极管整流桥、开关管S、二极管D、输出电容Co、电感L、电磁干扰(electromagnetic interference, EMI)滤波电容Cf、电感Lf。

图1 传统buck-boost PFC变换器及其控制
图2(a)、图2(b)分别给出了单电流闭环控制和含谐波注入的单电流闭环控制无桥buck-boost PFC变换器原理图。在无桥buck-boost PFC拓扑中,包括整流二极管DR1和DR2、开关管S1和S2、输出二极管D1和D2、电感器L1和L2、输出电解电容C1和C2以及双向中间电容C3。其中,S1、S2的驱动信号Vgs1、Vgs2可以完全相同,实现控制简化。

图2 提出的无桥buck-boost PFC变换器及两种控制方法
在无桥buck-boost PFC拓扑[22]中,由S1、D1、L1和S2、D2、L2组成的双buck-boost变换单元分别仅工作在正、负半个工频周期,变换器整体器件利用率不高。本文仅增加中间电容C3(如图2所示),可以使得双电感在半个工频周期内,分别工作于DCM与CCM,且未增加控制复杂性。
1.2 工作模态
为简化分析,作如下假设:1)所有器件为理想器件;2)工频周期远大于开关周期TS,输入电压vin在一个开关周期内可以认为是常数。
由于无桥buck-boost PFC变换器在正、负半个工频周期的运行模式相似,本文仅给出正半工频周期工作模态图,如图3所示。图4给出了半个工频周期与开关周期所对应的主要器件波形图。由图3与图4可知,所提出的buck-boost PFC变换器由于交流输入过零换流而存在两种工作阶段:

图3 提出的变换器交流换流时工作模态与主模态
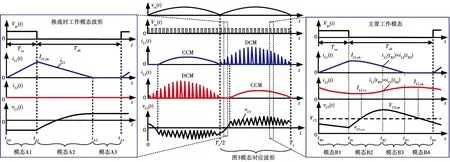
图4 不同工作模态的关键器件波形图
1)当交流输入处于过零换流阶段时,变换器中间电容电压vC3也需要完成换向;此时,变换器工作模态为A1~A3,vC3电压不断增大,且只有一个电感处于DCM;
2)当中间电容电压vC3足够大(即存储能量足够大)时,C3可以支撑闲置电感开始运行于CCM;此时,变换器开始运行于主要工作模态,其工作模态为B1~B4,且两个电感分别工作于CCM与DCM。
下边对第一、第二工作阶段分别进行介绍。首先介绍A1~A3工作模态对应的第一工作阶段。
工作模态A1[tA0~tA1]:如图3(a)所示,当S1导通时,vin对L1充电,iL1线性增大。同时,C1与C2为负载供能。此阶段,iL1增大,VC1、VC2减小。
工作模态A2[tA1~tA2]:如图3(b)所示,当S1关断时,iL1通过D1向C1、C3与负载供能,C2继续为负载供能。此阶段,iL1、VC2减小,VC1、vC3增大。
工作模态A3[tA2~tA3]:如图3(c)所示,S1保持关断,当iL1下降至0时,此工作模态开始。C1与C2为负载供能。此阶段VC1、VC2减小,vC3不变。
在工作模态A1~A3所示的第一工作阶段中,vC3不断增大,VC2不断减小,直到vC3>VC2时,电感L2的两端电压vL2不为0,变换器进入第二工作阶段,其工作模态为B1~B4。
工作模态B1[tB0~tB1]:如图3(d)所示,当S1导通时,vin对L1充电,iL1线性增大。同时,L2、C3、C1存储的能量向输出电容C2与负载传递。此阶段,iL2、vC3、VC1减小,iL1增大。
工作模态B2[tB1~tB2]:如图3(e)所示,当S1关断时,iL1通过D1向C1、负载供能。同时,iL1较大的电流会导致中间电容C3的电流方向瞬间突变。此时,iL1、iL2非线性减小,vC3非线性增大。当vC3增大并超过VC2,则由于vL2=VC2-vC3<0而导致iL1开始向L2充电,即iL2达到谷值iL2,va并开始增大。此阶段,iL1减小,VC1、vC3增大。
工作模态B3[tB2~tB3]:如图3(f)所示,S1保持关断,当iL1下降到与iL2相等时(即iC3=0,因为iL1=iL2+iC3),该工作模态开始。该阶段,vC3不断减小,且iC3(iL1 工作模态B4[tB3~tB4]:如图3(g)所示,S1保持关断,当iL1下降到0时,该工作模态开始。该阶段,iL1保持为0,L2、C3、C1存储的能量向输出电容C2与负载传递。此阶段,vC3、VC1非线性减小,iL2非线性增大。当vC3不断下降并小于VC2时,则由于vL2=VC2-vC3>0而导致iL1达到峰值IL2,pk,iL1开始下降。此阶段,VC1、vC3减小。 令输入电压峰值为VM,角频率为ω,则vin为 vin(t)=VMsin(ωt)。 (1) 开关管的平均电流iS1,ave可以看作输入电流iin,表达式为 (2) 式中:dL为电感的充电时占空比(即开关管的导通占空比);fS为开关频率;sin(ωt)的绝对值表示变换器工作于正半工作周期。 根据式(1)、式(2)可以推导瞬时输入功率pin与平均输入功率Pin为: (3) (4) 根据式(4)可以推导出导通占空比dL的表达式为 (5) 由式(5)可知,在理想条件下,由于L1、fS、Pin与VM是固定值,占空比dL也相对固定。另一方面,忽略由于使用EMI滤波器导致的输入电压与输入电流的相位偏移,可以推导变换器的理论PF为 (6) 式(6)表明,所提出的变换器在理想情况可以与传统buck-boost PFC变换器一样,实现高PF。这是由于所提出的变换器与输入侧连接时,其工作模态与传统变换器基本相同。 将输出星接电容等效为三角接电容,可以得到图5(a)所示的变换器工作等效电路图。其中C1、C2、C3与等效电容C1E、C2E、C3E的关系为: (7) 图5 提出变换器的等效电路 进一步地,可以将工作等效电路简化为如图5(b)所示的输出等效电路。在图5(b)中,相对于传统buck-boost PFC变换器,所提出变换器的输出等效电路增加了LC滤波、等效电容C1E。因此,理论上,具备实现更小的输出电流纹波的条件。 根据式(3)、式(4)可知,pin=2Pinsin(ωt)。输出二极管D1的平均电流iD1,avg可以表示为 Io-Iocos(2ωt)。 (8) 式中Io为输出电流平均值。为简化分析,仅对二倍工频谐波进行输出纹波分析,建立如图5(b)所示的输出等效电路。图5(b)中的等效阻抗Zeq可以采用诺顿定理推导得到,即 (9) (10) 由式(9)、式(10)可以得到输出二倍工频纹波在负载侧的表达式为 (11) 最后,变换器的输出电流纹波io,rip为 (12) 为反映输出纹波随电容、电感参数的变化情况,选取典型值Io=0.5 A,ω=100π rad/s,RL=50 Ω,C3=0.47 μF,RESR=20 mΩ。根据式(12)可以得到,输出纹波电流io,rip峰-峰值随输出电容C1、C2与电感L1、L2的变化曲面,如图6所示。由图可知,所提出的变换器输出纹波电流io,rip主要受到输出电容C1、C2影响,即电容值越大则输出纹波越小,符合输出电容越大对二倍工频纹波滤波效果越强的规律。另外,电感L1、L2对io,rip的影响比较小,表现为电感值越大则输出纹波越小。 通过在控制部分引入输入谐波分量可以实现输入功率因数与输出纹波的权衡控制[9-10]。这种控制本质是降低PF值至一定值(通常≥0.9),以实现更低的输出电流纹波。在实际应用中,较高的PF值不会带来经济效益,而较低的输出纹波可以让厂家选用更小容值的低成本电容达到同样的输出纹波要求,经济效益更高。 本文提出的无桥buck-boost PFC变换器同样可以采用这种PF与输出纹波的权衡控制,图2(b)给出了控制实现框图。这种谐波注入的控制策略,在输入功率Pin较小时,采用较大占空比;在Pin较大时,采用较小占空比,可以实现输入功率平滑传输至输出侧,减小输出纹波。具体占空比dL,H为 dL,H=adL(1-k|sinωt|)= (13) 式中a与k都是常数。 为确定a与k值,将式(13)中的dL,H代替式(4)中的dL,可以得到谐波注入控制下的Pin,H为 (14) 由于Pin=Pin,H,因此,由式(14)可得 (15) 当占空比由dL,H确定时,谐波注入控制下的PF为 (16) 根据式(16),图7给出了以k为变量的PF曲线。为保证PF≥0.9,k可以取0.607。由k=0.607,可以通过式(15)确定a=2.017,则式(13)中的dL,H为 (17) 图7 PF随k值的变化曲线 根据式(3)可以得到单闭环控制的无桥buck-boost PFC变换器瞬时输出电流为 io(t)=pin/Vo=Pin[1-cos(2ωt)]/Vo。 (18) 同理,根据式(18)可以得到含谐波注入的单闭环控制时的变换器瞬时输出电流为 io,H(t)= (19) 将式(18)、式(19)中的输出电流除以输出电流Io(Io=Pin/Vo)进行标幺化,可以得到 io(Norm)(t)=1-cos(2ωt); (20) io,H(Norm)(t)=4.068[1-0.607sin(ωt)]2× [1-cos(2ωt)]。 (21) 根据式(20)、式(21),图8给出了两种控制方法所对应的输出电流标幺值。可以看到,采用含谐波注入的单电流闭环控制方法可以减小输出电流的波动,降低输出电流纹波。但是,该方法的代价就是如图7所示的PF值仅大于等于0.9。 图8 两种控制方法输出电流标幺值 由于单级buck-boost PFC变换器通常应用于功率≤25 W的非隔离LED应用场合[4]。因此,为验证所提出的变换器可行性,分别构建了13 W的传统buck-boost PFC变换器(Conv.)和所提出的buck-boost PFC变换器(Prop.)实验样机。其中,传统buck-boost PFC变换器通过图1(a)所示的控制原理图实现。为保证控制环路参数的一致性以及实验简便性,样机均采用DSP TMS320F28335实现闭环控制。表1给出了关键电路参数,C1、C2串联,所以C1=C2=2C,VC1=VC2=1/2VC。图9给出了所提出的变换器实验样机,传统buck-boost PFC变换器实验样机基于同一PCB改造得到。开关管S、S1、S2为IPW65R125C7,整流和输出二极管为IDH06G65C5,电感L、L1、L2磁芯为美磁Kool Mμ77206A7,C、C1、C2均为电解电容,C3为MKT1822系列的薄膜电容。注意,由于输出电容C1和C2是串联的(见图2),因此,C1和C2的电容值应为C(见图1)的两倍,但是,C1和C2的耐压值仅为C的1/2。 表1 电路参数 图9 所提出的电感复用无桥buck-boost PFC变换器样机 在110 Vac输入电压时,分别对传统buck-boost PFC变换器与所提出的电感复用无桥buck-boost PFC变换器实验样机进行测试。表2给出了具体的实验结果对比。 表2 Buck-boost PFC变换器实验结果 图10给出了传统buck-boost PFC变换器的实验波形。由图10(a)、图10(b)可知,传统变换器的电感电流iL在每个交流工频周期中均运行于DCM,开关管漏源两端电压Vds包络线跟随整流后输入电压Vd。结合图10(c)可知,这种传统变换器可以采用简单的单电流环实现稳定运行与输入电流高正弦性。 图10 传统buck-boost PFC变换器在单电流环控制时的实验波形 图11给出了所提出的电感复用buck-boost PFC变换器在单电流环控制下的实验波形。由图11(a)、图11(b)可知,在半个工频周期内,电感电流iL1、iL2分别交替工作于DCM与CCM,验证了变换器电感的双工作模态;且中间电容电压vC3经过短暂的换流后,与工作于CCM的电感电流形成如图4所示的能量交互,即中间电容C3与CCM电感组成滤波网络实现变换器低输出纹波特性。另外,结合图11(c)可知,所提出的变换器在单电流环控制下的输出电流纹波为190 mA,与图6所示的理论计算值(206 mA)接近(注:由于器件参数偏差与测量误差等因素,理论计算值与实际测量值存在一定的偏差)。 图11 提出的无桥buck-boost PFC变换器在单电流环控制时的实验波形 图12给出了所提出的变换器在含谐波注入时的单电流环控制下的实验波形。由图12(a)、图12(b)可知,变换器电感仍然交替地工作于DCM与CCM,未受到谐波注入的影响。结合图12(c)可知,在这种谐波注入控制方式下,变换器输入电流iin有所畸变,但是变换器PF值维持在0.908,与图7的理论计算值(PF≥0.9)接近,验证了参数设计的准确性。 图12 提出的无桥buck-boost PFC变换器在含有谐波注入控制时的实验波形 在输出电流纹波io,rip方面,对比图10(c)和图11(c),所提出的变换器输出电流纹波(190 mA)比传统变换器(220 mA)更小。这是因为所提出变换器的一个电感与中间电容C3构成了LC滤波,可以进一步减小输出纹波。另外,对比图11(c)和图12(c),输出电流纹波io,rip由190 mA降低到了140 mA,降低了35.7%,验证了所提出变换器在含谐波注入控制时,可以实现更低的输出电流纹波。 在PF、THDi方面,传统变换器的PF和THDi分别为0.998和2.9%。相应地,所提出的变换器在同样的单电流闭环控制时,PF和THDi分别为0.998和3.3%。两种变换器的测量数据相近,表明当所提出的变换器与传统变换器使用同样的控制策略时,他们具有几乎相同的PF和THDi性能。此外,如2.3节所述,当所提出的变换器使用含谐波注入的控制时,通过设置a、k,可以保证变换器的PF值高于0.9(实验中为0.908),但是其输出电流纹波仅为140 mA,验证了参数设计与理论分析的正确性。 在效率方面,当所提出的变换器采用无谐波注入控制时,变换器的测量效率为81.3%,当采用谐波注入控制时,该变换器的测量效率为80.1%。这是因为在含谐波注入的控制时,更多的输入电流谐波会流入变换器,降低了变换器效率。另一方面,传统变换器的测量效率仅为78.1%。即所提出的无桥buck-boost PFC变换器在含谐波注入控制时、不含谐波注入控制时的效率都略高于传统变换器。 本文提出一种双电感复用无桥buck-boost PFC变换器,提高了双变换单元在无桥拓扑中的器件利用率。在半个工频周期内,双电感分别交替工作于DCM、CCM,且不需要复杂的控制、额外的辅助电路。工作于DCM的电感,使变换器可以采用单闭环控制实现高PF与输出电流调节;工作于CCM的电感,与中间电容构成额外滤波电路,减小变换器输出纹波。此外,该变换器仍然可以采用含谐波注入的控制方法,通过主动降低PF至0.908,可降低35.7%的输出电流纹波。实验样机验证了理论分析的正确性。2 变换器PF与输出纹波性能分析
2.1 PF分析
2.2 输出纹波与参数分析

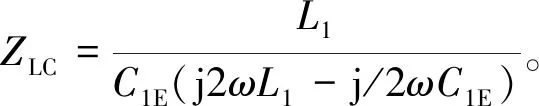
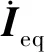
2.3 谐波注入控制

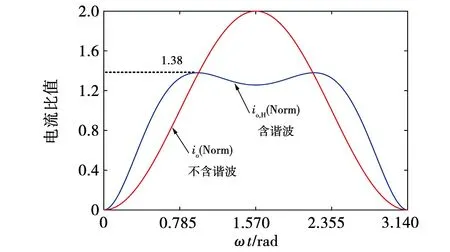
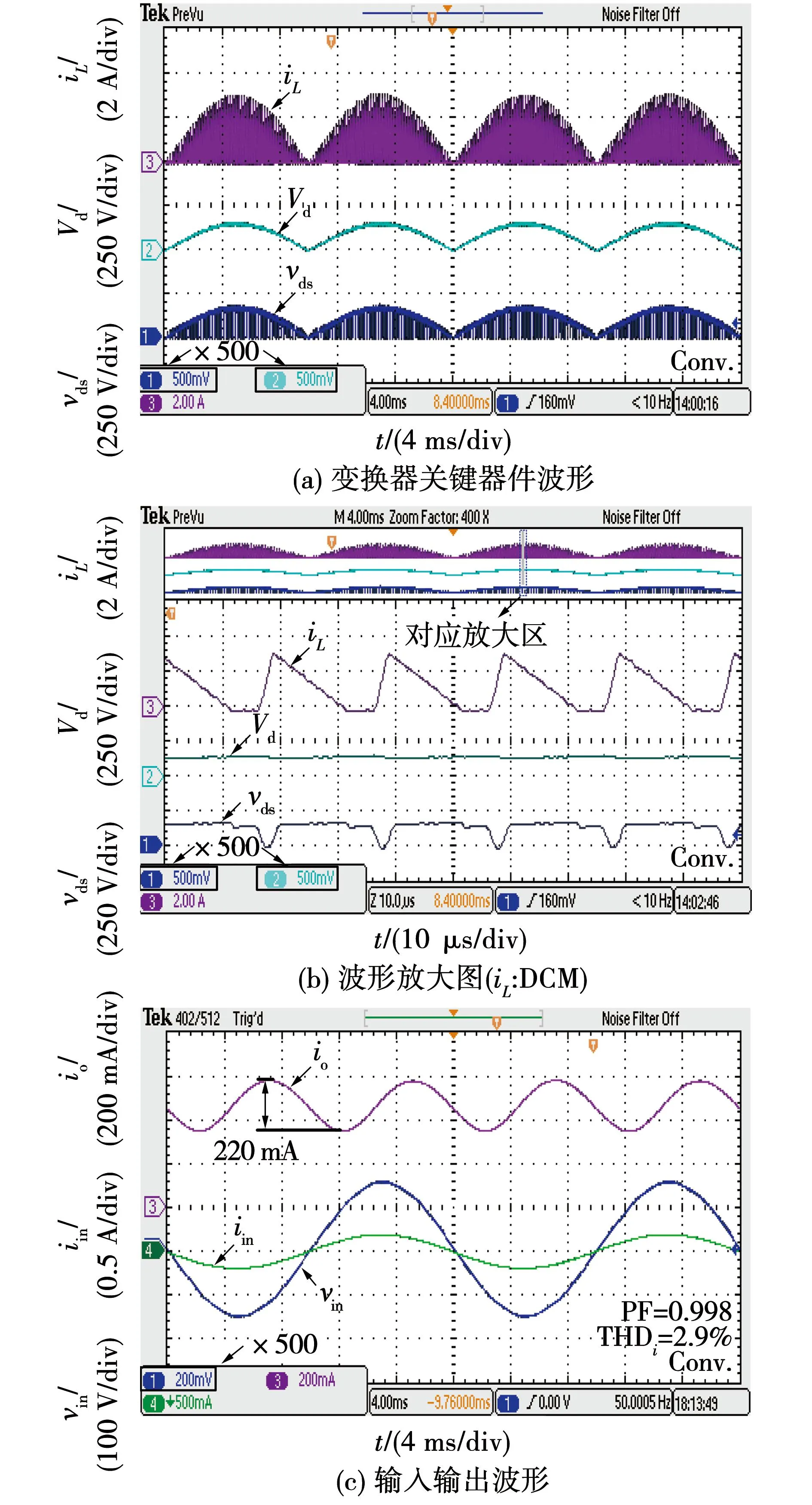
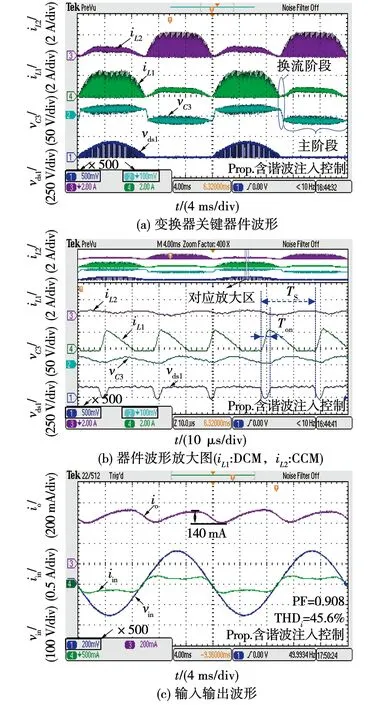
3 实验验证




4 结 论

