考虑铁损的同步磁阻电机最小损耗控制策略

赵子安, 王一帆, 李凤姣, 沈传文

(西安交通大学 电气工程学院,陕西 西安 710000)

0 引 言

相较于永磁同步电机,同步磁阻电机(synchronous reluctance motors,SynRMs)因转子无永磁体或绕组使其结构更为简单,制造成本更低,便于生产。此外,其还具有功率密度大、转矩密度高、鲁棒性强和控制简单等优点,因而近些年来逐渐成为研究热点[1-3]。除电机结构外,同步磁阻电机的运行性能还受到控制策略的影响。矢量控制作为一种较为成熟的控制策略被广泛的应用于电机的控制中[4]。电机的矢量控制中最重要的参数是定子电流与d轴的夹角θ,即定子电流在d-q轴上的分配方式。不同的分配方式对应同步磁阻电机不同的电流控制策略[5]。同步磁阻电机的电流控制策略主要有最大转矩电流比控制(maximum torque per ampere,MTPA)和最小损耗控制(minimum losses,ML)[6]。

传统的MTPA控制策略通常忽略同步磁阻电机d轴和q轴电机参数变化所带来的影响[6-8],即定子电流在d轴与q轴上的分配量相等,电流角θ取45°[9-11]。此时的控制算法较为简单,但在高速或重载条件下转速与转矩会产生较大的控制误差[7]。为解决上述问题,文献[12]改进了传统的MTPA控制策略,通过注入高频信号实现对d-q轴电流的计算。文献[13]实现了基于磁场定向控制的MTPA控制,解决了独立控制d轴和q轴电流时电流过大的问题,改善了电机的动态性能。此外,为了降低复杂控制策略所带来的计算负担,查表法被应用于MTPA的控制中。文献[14]利用离线测量和控制模型简化建立了MTPA电流查找表,有效降低了计算负担。然而,上述文献中均使用常规的同步磁阻电机等效电路,忽略了实际运行中铁心损耗对电路带来的影响。在常规电路等效模型中,电机转矩和磁通直接由定子d-q轴电流控制,输入定子端电流也仅由转矩电流决定,但高速运行引起的铁心损耗增大会导致定子磁链电流和转矩电流耦合。此时如果仅考虑d-q轴电流,转矩将无法精确控制[15],并且由于此时定子端电流由定子磁链电流和转矩电流两部分决定,常规的MTPA控制策略将无法满足实际使用的需要。

考虑转子铁心损耗的电机模型为实际运行下的定子电流提供了更为准确的表述,便利了对d-q轴电流准确分配的控制。进而,通过分析电机模型的电流可以精确描述系统的能量损耗,在此基础上提出的最小损耗控制策略可以在保持电机输出充足转矩的同时将系统的损耗最小化[16],有效提高电机的运行效率。为实现对电机的最小损耗控制,文献[17]引入了电路中的铁损计算,改进了永磁辅助同步磁阻电机中绕组的励磁损耗。文献[16,18-20]在考虑铁损电阻的基础上提出了新的电机损耗模型,实现了同步磁阻电机的最小损耗控制。文献[18]重点介绍了饱和度和铁损耗对矢量控制的影响,但未给出详尽的电流分配公式。文献[16]给出了电流同电磁转矩的拟合公式,其依赖对单一被控电机的大量离线实验使应用过程较为繁琐。文献[19]利用信号注入的方式实现了电机的最小损耗控制。文献[20]利用有限元分析确定电机损耗模型的各参数特性并通过人工神经网络进行电流分配,其同样需要大量的离线实验且控制计算负担较大。

基于上述分析,具体分析同步磁阻电机运行原理和控制策略,提出一种考虑铁心损耗的同步磁阻电机模型,并基于此模型推导考虑铁损的同步磁阻电机最小损耗控制策略。所提出的控制策略可使电机实现更高的工作效率。

1 同步磁阻电机的数学模型

1.1 传统同步磁阻电机模型

在不考虑磁滞与涡流损耗且假设电机转子空间磁场为正弦分布,定子铁心不饱和时,在d-q坐标系下同步磁阻电机等效数学模型如图1所示。

图1 忽略铁心损耗时同步磁阻电机等效d-q轴电路模型

此时可写出在d-q参考坐标系下同步磁阻电机的电压和电磁转矩数学模型:

(1)

(2)

式中:vd、vq分别为d轴和q轴的电压;id、iq分别为d轴和q轴的电流;Ld、Lq分别为d轴和q轴的电感;ωr为电角速度;Rs为定子电阻;P为极对数,p为微分算子;Te为电机的电磁转矩。

1.2 考虑铁心损耗的电机模型

为了对电机损耗进行更为准确的分析,需要将同步电机每相并联一个铁损电阻Rm来对电机的铁心损耗进行考虑[20]。此时,同步磁阻电机的电路结构可等效如图2所示。

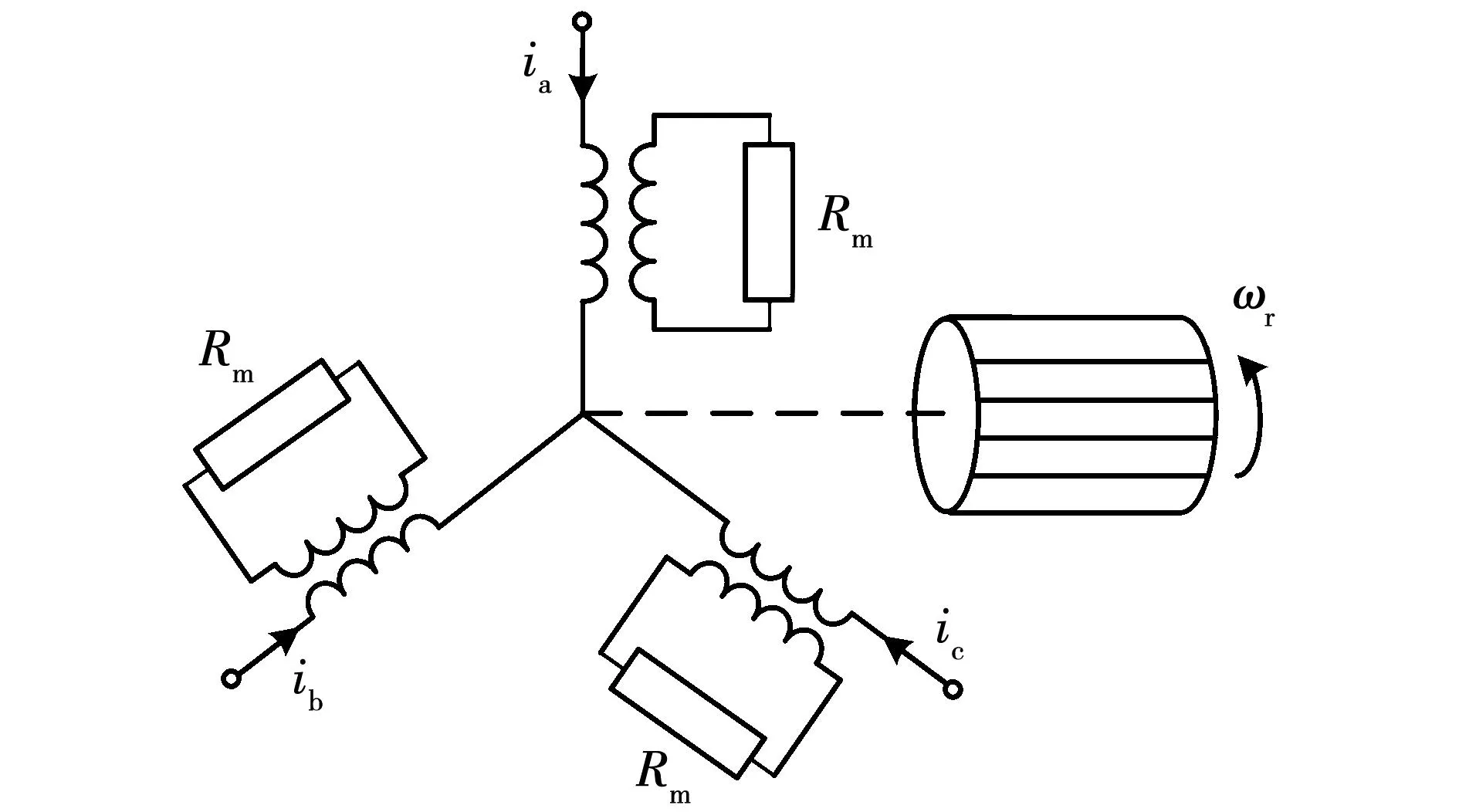
图2 考虑铁损的同步磁阻电机电路等效结构

这样,就可以写出电机内部三相电流iabc=[ia,ib,ic]T和三相电压vabc=[va,vb,vc]T的数学表达式如下:

(3)

vabc=vabcm+Rsiabcm。

(4)

式中:iabcm=[iam,ibm,icm]T为铁损电阻支路上的三相电流;vabcm=[vam,vbm,vcm]T为铁损电阻支路上的三相电压;λabcm=[λam,λbm,λcm]T为铁损电阻支路上的三相磁链。将式(3)及式(4)通过坐标变换可将相电流和相电压方程转化到d-q转子坐标系下,此时相电流与相电压的矩阵形式为:

(5)

vqdn=Rsiqdn+vqdnm。

(6)

展开后可得:

(7)

(8)

vd=Rsid-ωLqiqs+pLdids;

(9)

vd=Rsiq+ωLdids+pLqiqs。

(10)

式中:ids和iqs分别为通过d轴和q轴电感Ld和Lq的电枢电流。

根据能量守恒原则,相应可得电机的电磁转矩为

(11)

由式(7)～式(10)可得出在d-q转子坐标系下考虑铁心损耗的电机d轴与q轴的等效电路如图3所示。与忽略铁心损耗的电机等效电路相比,其增加了一个同旋转电动势与瞬态磁链支路并联的电阻Rm来计算铁心损耗,d-q两相铁损电阻可视为等值电阻。由于铁损电阻的加入,定子两端输入支路上增加了铁损电流idm和iqm。此时,电磁转矩不再由两相定子输入电流乘积决定,而是取决于电枢电流ids和iqs的乘积。

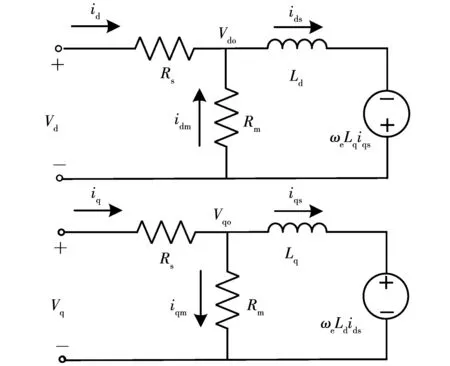
图3 考虑铁心损耗时同步磁阻电机等效d-q轴电路模型

1.3 考虑铁心损耗电机模型的铁损电阻计算模型

引入铁损电阻的目的在于表征铁心损耗,因此可通过分析电机运行时的能量输入输出关系来得到铁损电阻的表达式。为方便分析,考虑电机空载运行时,其铁损与输入功率,输出功率以及铜损有如下关系:

Pi=Pin-Pout-Pc。

(12)

式中:Pi为电机的铁损;Pin为输入功率;Pout为输出功率;Pc为电机的铜损。

根据图3的考虑铁损的电机等效模型可得

(13)

其中Vdo和Vqo为电机反电动势电压,其计算公式为:

(14)

计算得到铁损电阻Rm为

(15)

这样就得到了铁损电阻的模型。

2 传统同步磁阻电机MTPA控制

在不考虑电机铁损时,d-q参考系下两项电流id及iq存在如下关系:

(16)

即

(17)

式中:Is为输入电流矢量幅值;δ为输入电流矢量同d轴的夹角。

将式(16)代入式(2)可得

(18)

同步磁阻电机MTPA控制策略的目标是使用一定幅值的定子电流使输出电磁转矩实现最大。由式(17)及式(18)可以看出当输入定子电流幅值一定时,输出电磁转矩大小仅与电流角δ相关,为实现同步磁阻电机的MTPA控制,要求电磁转矩对电流角的偏导为0[21]。此时有

(19)

忽略d、q轴电感值随电流角的变化[22],可得

(20)

由上式得出,取到电磁转矩对电流角的偏导为0,此时电机运行在MTPA状态。通过式(2)可得出其工作点为

(21)

可以看出电机的d轴与q轴电流等值且仅与电磁转矩的平方根成正比而与电机转速无关。其控制系统的方框图可建立如图4所示。

图4 传统MTPA系统电机控制框图

3 考虑铁损时的最小损耗控制

在第2节中介绍了不考虑同步磁阻电机铁损的情况下传统MTPA控制的实现过程。然而在电机实际运行过程中转速过高会导致铁损增大从而降低总损耗中铜损的权重进而导致定子磁链电流和转矩电流耦合,这对电机的最优工作点的选取造成影响[23]。为解决上述问题,实现电机运行时总损耗的最小化,本文考虑电机的铁损数学模型,推导出了以一定转矩下电机的总损耗最小为目标的最小损耗控制策略作为优选方案。

在忽略机械损耗的情况下,电机损耗由电枢电阻上的损耗和铁心损耗组成,即由铜损和铁损组成,其表达式为

(22)

此时式(22)为最小损耗控制目标函数,在满足式(16)时可以通过合理分配d轴和q轴的电枢电流使电机运行的总损耗达到最小。在给定转矩和转速的情况下,可以得到最小损耗控制的工作点为:

(23)

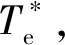
为更为直观展示控制效果,引入文献[24]提出的考虑铁损的同步磁阻电机MTPA控制策略作为对比,该控制策略下电机给定电机的工作点为:

(24)

电机在给定1.5 N·m转矩下,电机总损耗图如图5所示。根据式(23)和式(24)可知,在一定转矩下MTPA与最小损耗控制策略的d-q两相输入电流不再保持恒定,而是随电角速度ωe发生变化。仅在ωe=0,即电机启动时,两种控制策略的电流分配与未考虑铁耗时相同。由图5所示,最小损耗策略控制下的电机损耗恒小于MTPA控制策略,且两者差距也随着ωe上升而逐渐变大。由于输出功率一定,最小损耗控制效率在全速度范围内均高于MTPA。

从能量角度来看,MTPA控制确保了电机输入电流的平方和最小,因此其实质上是铜损最小策略,在转速较低时,铜损在总损耗中权重较大,因而两种控制策略工作点较为接近,电机损耗功率差距较小;随着转速不断上升,铁损在总损耗中的权重不断上升,此时两种电流控制策略工作点差异变大,电机损耗功率差距也变大。

4 仿真验证

为验证本文提出的最小损耗控制理论的正确性,在MATLAB/Simulink仿真平台上搭建了同步磁阻电机与控制系统的模型,其结构如图6所示。内置电机参数如表1所示。

表1 同步磁阻电机参数

图6 考虑铁损场景下的最小损耗控制框图

图7和图8分别为2 s时突加1.5 N·m负载后在MTPA控制和最小损耗控制下电机转速与转矩变化的情况,初始时电机空载,转速为1 500 r/min。

图7 负载突变时电机转速变化

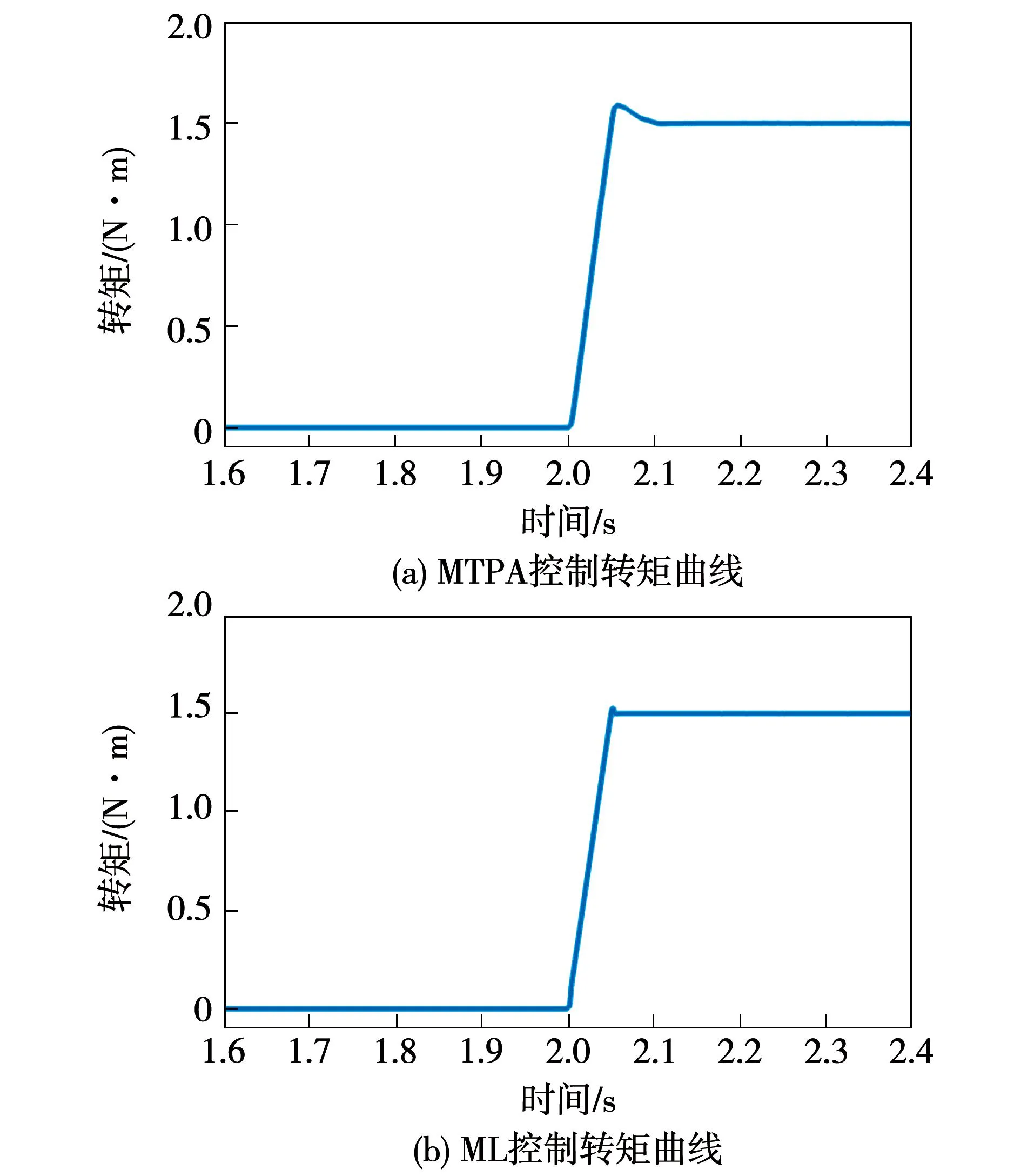
图8 负载突变时电机转矩变化

可以看出,在两种控制策略下,施加负载转矩后的电机转速均略有跌落并能快速恢复至给定值。此外,提出的最小损耗控制策略的简洁性使电机转速恢复与转矩增大过程中均有更快的响应与更小的超调,因而具备更好的暂态性能。

图9展示了电机运行过程中的功率损耗情况。系统运行在1 500 r/min,转矩为1.5 N·m时,MTPA策略控制下的电机损耗功率为105.5 W,最小损耗控制策略控制下的电机损耗功率为79.2 W,这同利用式(22)计算得到的电机损耗功率99.7 W与77.6 W的结果相近似。ML控制下可节约8.35%的能量损耗。显然,最小损耗控制策略控制下电机总损耗更小且主要体现在铁损的减少方面。

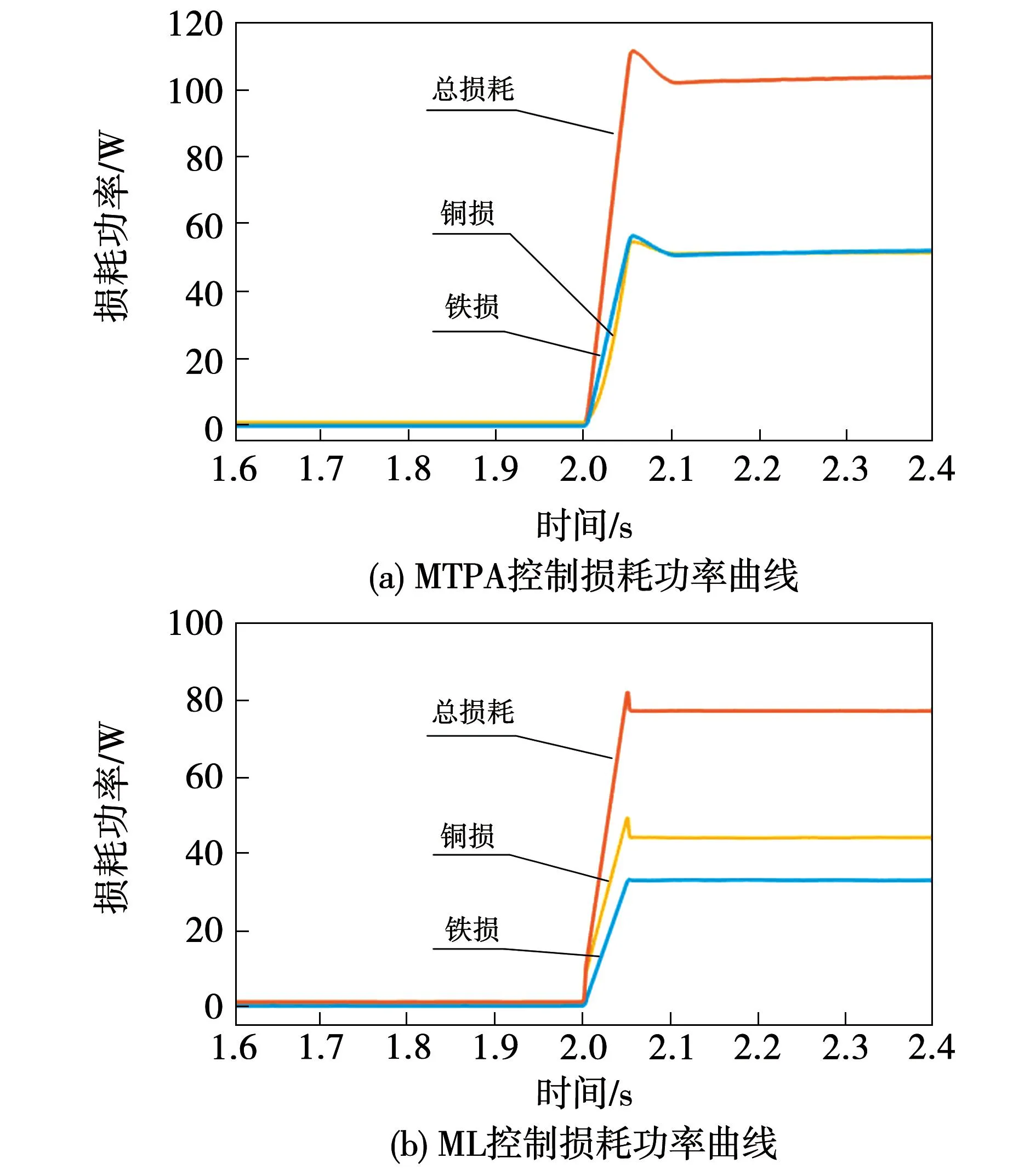
图9 负载突变时的电机损耗

5 实验验证

为进一步验证所提出的考虑铁损的ML控制策略的有效性,设计并搭建了如图10所示的对拖实验平台。图中所示标号1为0.55 kW同步磁阻电机,其参数如表1所示;标号2为0.75 kW的永磁同步电机作为负载电机;标号3为负载电机的驱动装置;标号4为单相交流驱动电源;标号5为编码器信号采集及逆变器驱动装置;标号6中的主控制器为德州仪器公司(TI)的控制芯片TMS320F28335。

图10 同步磁阻电机驱动控制系统实验平台

图11和图12为负载发生改变时,MTPA控制和所提出的ML控制策略下电机输出转矩和转速的变化情况。电机初始转速为1 500 r/min,初始负载转矩为0.45 N·m。在2.5 s突加负载至1.5 N·m。

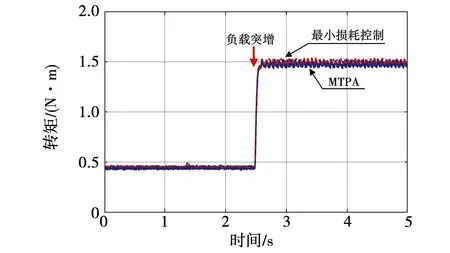
图11 电机突加负载时转矩波形图

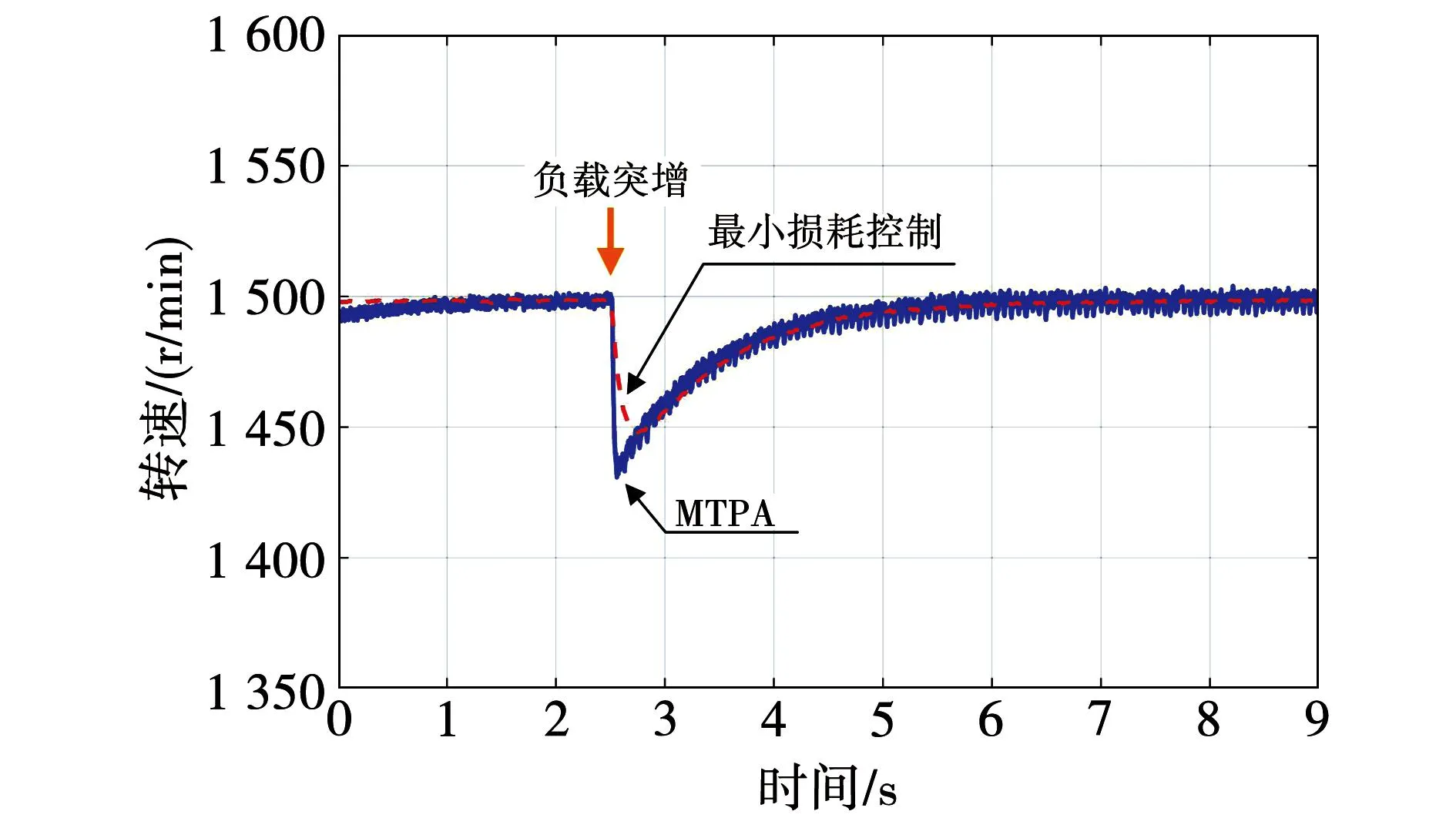
图12 电机突加负载时转速波形图

可以看出,两种控制策略均可满足负载突变情况的转矩需求。在电机输出转矩上升至1.5 N·m的过程中,电机初始转速略有跌落但很快恢复参考值。在MTPA控制下,电机转速跌落至1 431 r/min,约3.5 s后电机转速稳定至1 500 r/min;在最小损耗控制下,电机转速跌落至1 448 r/min,约3.5 s后电机转速稳定至1 500 r/min。

在平稳运行时两种控制下电机的电流,损耗以及效率对比如表2所示。可以看出,在一定负载转矩下考虑铁损的ML控制节约了约9.79%的能量损耗从而有效提升了电机的运行效率。

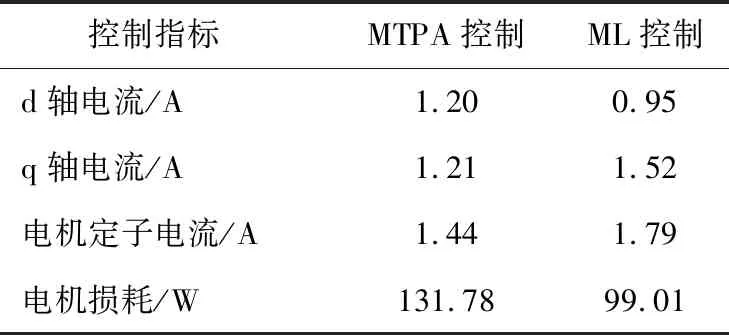
表2 两种控制下电机运行电流、损耗及效率对比

6 结 论

本文基于建模铁损电阻建立了考虑铁心损耗的同步磁阻电机模型,该模型准确表述了电机运行时定子电流的分配情况,更加贴近实际电机。在此基础上提出的考虑铁损的最小损耗控制策略实现了对输入电流的合理分配,使电机实现更高的工作效率。仿真与实验结果验证了所提出控制策略的有效性和可行性。