基于不等匝绕组的交替极永磁电机转矩脉动抑制技术

李烽, 王凯, 朱姝姝, 刘闯, 高培伟, 孙海阳

(1.南京航空航天大学 民航学院,江苏 南京 211106; 2.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027;3.南京航空航天大学 自动化学院,江苏 南京 211106; 4.南京林业大学 信息科学技术学院、人工智能学院,江苏 南京 211106)

0 引 言

随着高磁能永磁材料的发展和加工制造工艺的提高,使永磁电机兼具了低转矩脉动、高转矩密度、高功率因数和高效率等优点[1-2]。目前,永磁电机被广泛应用于国防军工、航空航天、风力发电和新能源电动汽车等领域[3-4]。

永磁电机需要大量的稀土材料保证电机的高转矩密度,然而,稀土材料是不可再生的战略储备资源且价格昂贵[4-5]。因此,越来越多的学者对交替极永磁电机开展了研究,交替极永磁电机即一组极性相同或相异的永磁体被凸极铁心替换,该电机具有低成本、低转矩脉动和高转矩密度等优点。国内外学者对交替极永磁结构在转子永磁型[6-10]和定子永磁型电机[11-14]中的应用开展了深入的研究。相比传统永磁电机,交替极永磁电机可节约33%永磁材料,转矩密度基本不变[6];文献[11]指出在磁通反向电机中采用交替极电机结构可节约50%永磁材料,同时电机的转矩密度也可提高26%。

虽然采用交替极永磁结构可节约永磁材料,降低电机加工成本,但是交替极永磁结构会导致电机的空载气隙磁密不对称,产生气隙磁密偶次谐波,若极槽配合选择不当会影响电机的反电势波形质量,增大电机的电磁转矩脉动,恶化转矩品质[15]。文献[16]指出:当Ns/t为奇数(Ns为电机定子槽数,t为单元电机数)时,不对称的空载气隙磁密会导致反电势偶次谐波,当电机通正弦交流电时,反电势偶次谐波与基波电流相互作用会产生较大的奇次转矩脉动。因此,为了消除此类交替极永磁电机反电势中的偶次谐波,模块化定子结构[17]、N-S-铁-S-N-铁转子结构[8]和混合转子结构[9]相继被提出,有效消除了电机的奇次电磁转矩脉动。

针对以9槽8极和9槽10极为单元电机的交替极永磁电机,文献[18]提出了一种四层绕组(four layer winding,FLW-1)结构,通过把两套绕组空间上错位一个定子齿,即可抑制交替极永磁电机的反电势偶次谐波,但是无法完全消除,电机的反电势波形质量有待进一步提高。为此,本文提出一种不等匝四层绕组(FLW-2)结构,以消除交替极永磁电机的2次和4次反电势谐波,减小电机的3次电磁转矩脉动,提高电磁转矩品质。

基于电机的反电势谐波星形图,本文阐述FLW-2交替极永磁电机的2次和4次谐波消除原理,并给出最优的绕组匝数比确定方法。对FLW-2交替极永磁电机的反电势波形进行谐波分析,验证FLW-2绕组结构的反电势偶次谐波消除原理,进一步分析不同绕组连接方式下电机的转矩特性,验证交替极永磁电机采用FLW-2绕组消除转矩脉动的有效性。

1 电机结构和反电势星形图

本文选用以9槽10极为单元电机的27槽30极电机,传统和交替极永磁电机的结构和绕组连接分别如图1(a)和图1(b)所示,电机的反电势星形图如图2(a)所示。由图1(a)可知:该电机由3个单元电机组成,每个单元电机的相反电势矢量数为3,正负相带中的属于同相的反电势矢量数不相等,当电机采用交替极永磁转子时同相绕组中感应出的反电势偶次谐波无法抵消,导致电机存在反电势偶次谐波,电机正弦波电流供电时,会增加电机的奇次电磁转矩脉动。

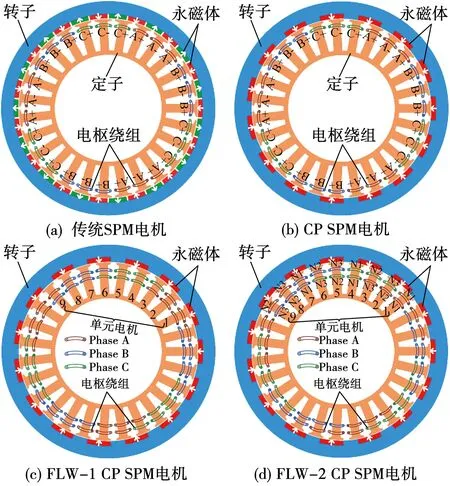
图1 双层和四层绕组CP PM电机截面和绕组分布图

图2 双层和四层绕组永磁电机的反电势星形图

FLW-1绕组结构的交替极永磁电机截面和绕组分布如图1(c)所示,图中单元电机定子齿标号与图2(b)反电势星形图中的反电势矢量一一对应。图1(c)中定子齿上的电枢绕组平分为内圈和外圈两套绕组,与之对应的是图2(b)中分为内圈和外圈两套反电势矢量。以A相反电势矢量为例,内圈A+和A-为第一套绕组(W1),外圈A++和A--为第二套绕组(W2),两套绕组空间上偏移一个齿即可抑制反电势中的偶次谐波[16]。

FLW-2绕组结构的交替极永磁电机截面和绕组分布如图1(d)所示,图2(c)是该电机的反电势星形图,图中对定子齿上的线圈匝数进行了标注。定子齿上内圈和外圈的电枢绕组空间上错位两个定子齿。FLW-2结构在两套绕组偏移的同时,线圈通过不等匝设计可以实现反电势低次(2次和4次)谐波的消除,第2节将对其消除原理和绕组最优匝数比确定方法进行详细介绍。

表1给出了传统和四层绕组交替极永磁电机的主要结构参数,表中I、II、III和IV分别表示传统SPM电机、CP SPM电机、FLW-1 CP SPM电机和FLW-2 CP SPM电机。

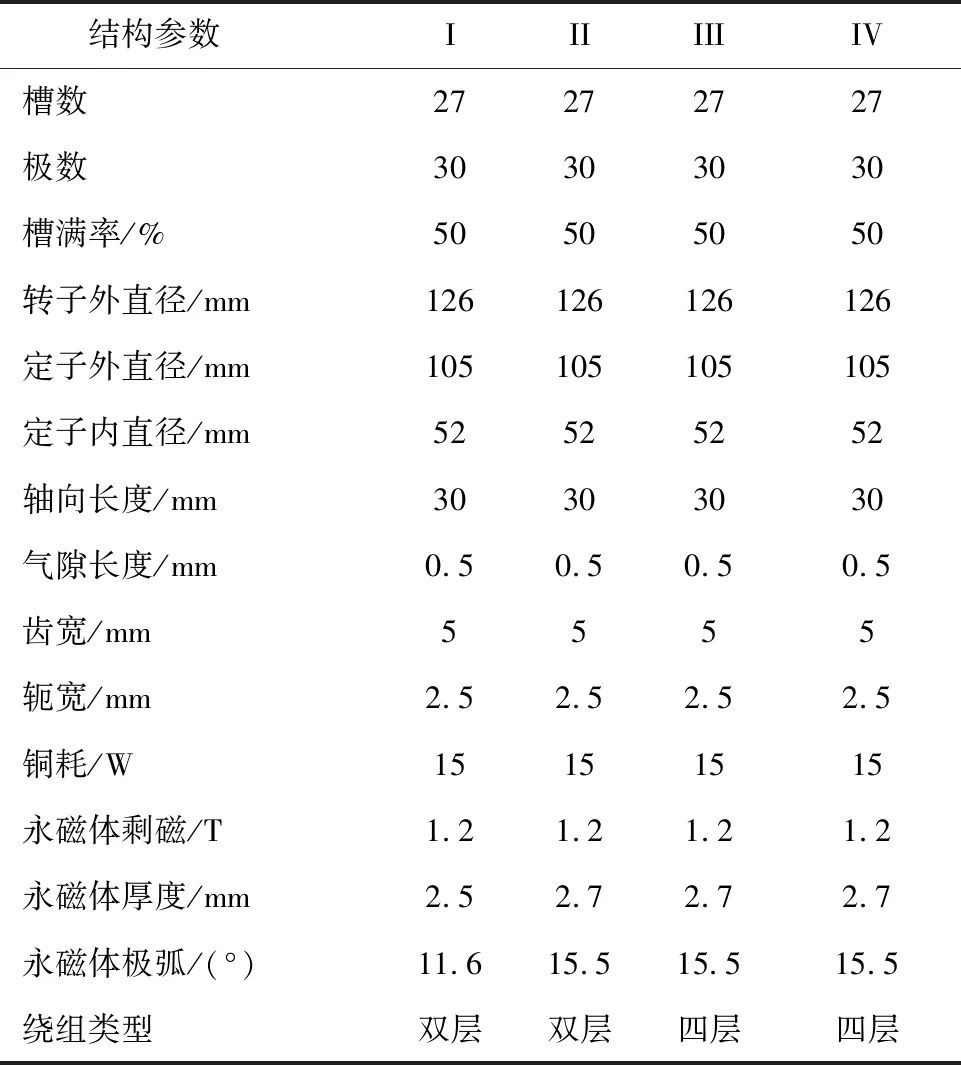
表1 永磁电机参数

2 不等匝绕组反电势偶次谐波消除原理

本节将采用反电势谐波矢量图阐述低次(2次和4次)谐波的消除原理,并给出FLW-2绕组的最优线圈匝数确定方法。图3(a)～图3(c)分别是FLW-2绕组相反电势的基波、2次和4次谐波星形图。由图3(b)和图3(c)可知:若要消除反电势中的2次和4次谐波,则其分布系数须为0,故线圈绕组匝数应满足以下条件:

(1)

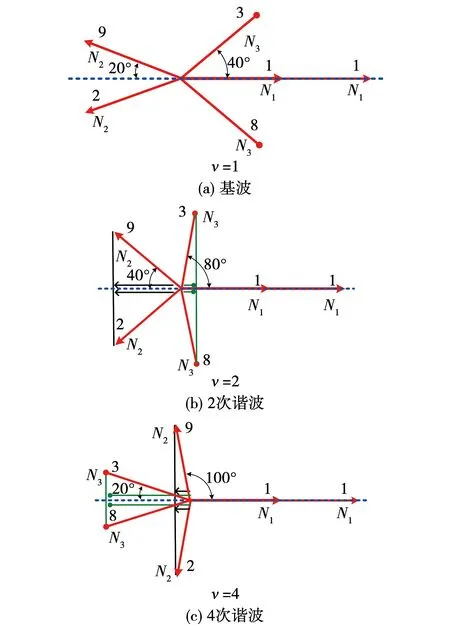
图3 基波、2 次和4次反电势谐波星形图

式中:kd_v=2和kd_v=4分别是2次和4次反电势谐波的分布系数;Ni(i=1、2、3)是相对应的绕组线圈匝数,由式(1)可知N1、N2和N3之间满足如下关系:

N2=2N1×0.742;N3=2N1×0.395。

(2)

由式(2)可知:N1、N2和N3选取合适的绕组匝数可以完全消除2次和4次反电势谐波。本文中传统永磁电机每个定子齿上线圈绕组匝数设计为22匝,为了保证FLW-2交替极永磁电机的线圈绕组匝数与传统永磁电机保持一致,线圈匝数N1、N2和N3需满足以下约束条件:

2×(N1+N2+N3)=3×22。

(3)

将式(2)代入式(3),计算可得N1=10.08,N2=14.84,N3=7.9,对线圈匝数取整,N1、N2和N3分别为10、15和8,如表2所示。

表2 永磁电机绕组参数

3 FLW-1和FLW-2交替极永磁电机反电势对比分析

图4(a)和图4(b)分别给出了FLW-1两套绕组(W1和W2)的相空载反电势波形和谐波分析结果,此时电机工作在额定转速300 r/min。由图4(a)可看出W1和W2绕组的反电势波形叠加后可以改善波形的对称性;图4(b)的谐波分析结果表明FLW-1可以有效抑制反电势中的低次谐波,特别是2次谐波。但是,2次谐波无法完全消除,当电机正弦波电流供电时会导致较大的3次电磁转矩脉动,降低转矩品质。

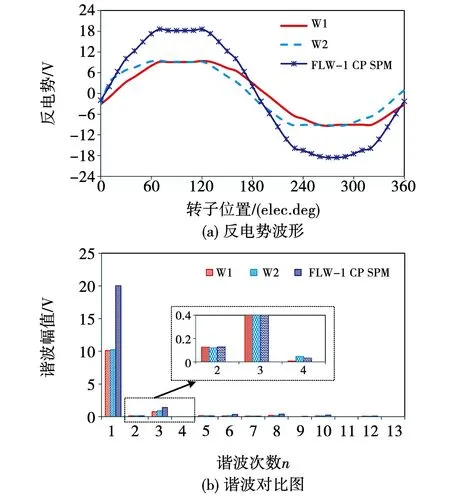
图4 FLW-1绕组的空载反电势

图5(a)和图5(b)分别给出了电机工作在额定转速时FLW-2两套绕组(W1和W2)的相空载反电势波形及其谐波分析结果。由图5(a)可知两套绕组产生的反电势波形形状完全相同,仅相位不同且二者的合成波形对称性相比FLW-1交替极永磁电机有较大改善,图5(b)的谐波分析结果也表明该电机的反电势2次谐波相比FLW-1交替极永磁电机有明显下降,会削弱电机的3次电磁转矩脉动,有利于改善电机的电磁转矩品质。电机采用FLW-2绕组,其绕组基波分布系数为0.916,绕组系数相比传统双层绕组和FLW-1绕组分别下降0.057和0.043,电机的反电势基波幅值会略有下降。

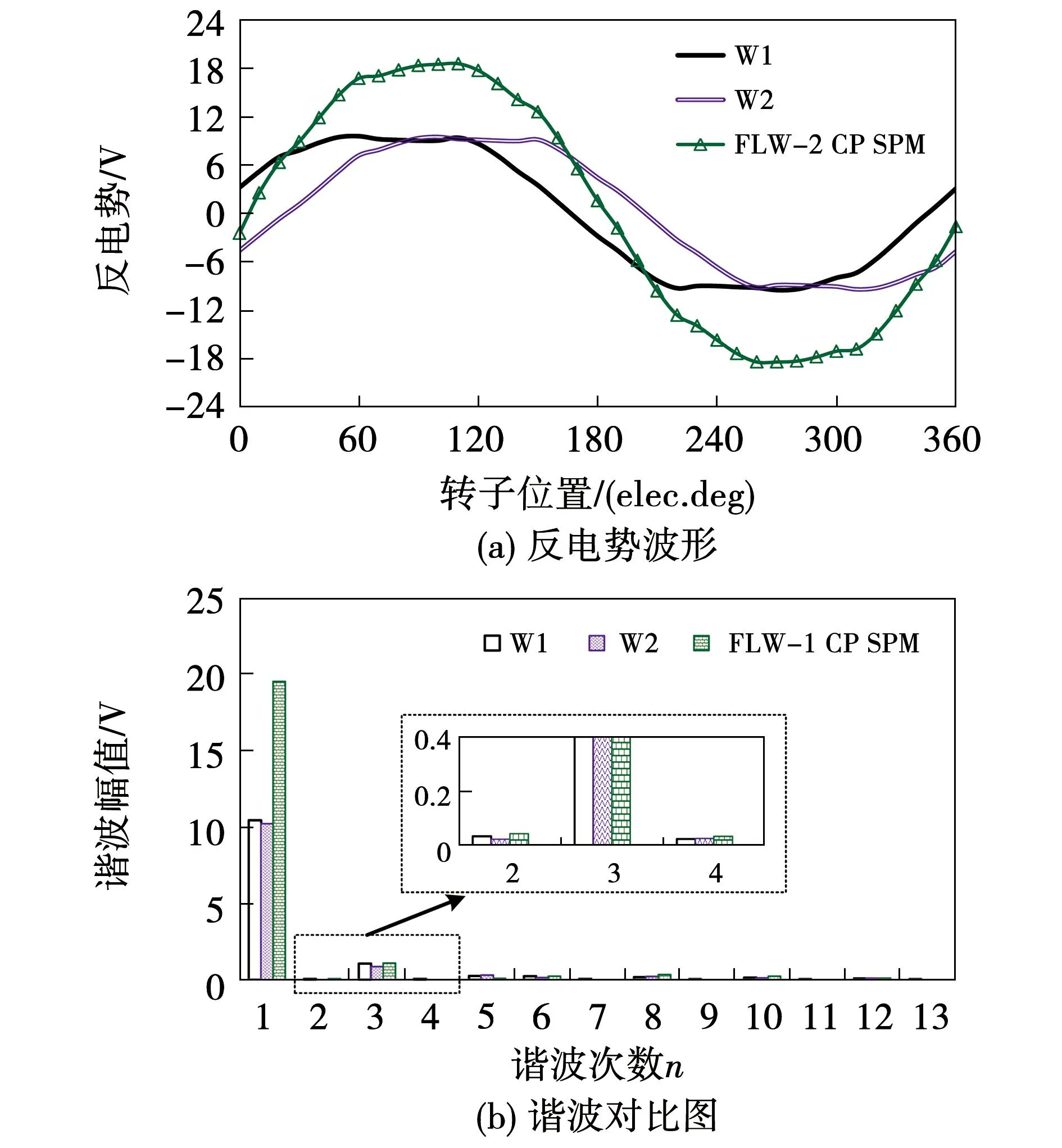
图5 FLW-2绕组的空载反电势

4 电磁性能分析

本节将分析传统双层绕组、FLW-1和FLW-2绕组交替极永磁电机,以及传统永磁电机的空载磁密分布特性、空载反电势特性和电磁转矩特性等电磁性能。因本文的重点是研究FLW-2绕组结构对交替极永磁电机电磁转矩脉动的影响,故不同绕组连接方式下交替极永磁电机的定转子结构参数、永磁体尺寸和槽开口等参数保持一致,如表1所示。

4.1 空载特性分析

传统永磁电机的空载磁场分布如图6(a)所示,由于双层绕组、FLW-1和FLW-2绕组交替极永磁电机定转子结构相同仅绕组连接方式不同,故它们的空载磁场分布相同,如图6(b)所示。由图6(b)可看出转子上经过永磁体和转子凸极铁心的磁力线不再对称分布,同时转子上的凸极铁心的局部会出现饱和现象,这会直接导致空载气隙磁密波形正负不对称,如图7(a)所示。空载气隙磁密的谐波分析结果如图7(b)所示,可知交替极永磁转子会导致大量的气隙磁密偶次谐波。

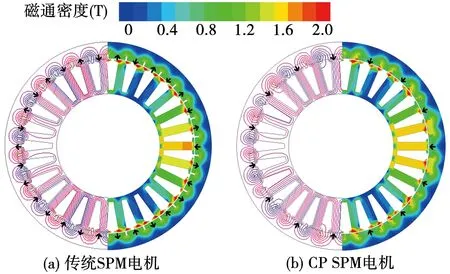
图6 传统和CP PM 电机的空载磁场分布

图7 传统和CP PM 电机的空载气隙磁密

传统双层绕组、FLW-1和FLW-2绕组交替极永磁电机、以及传统永磁电机的空载反电势波形和谐波分析结果分别如图8(a)和图8(b)所示。由图8(a)可看出双层绕组交替极永磁电机相比传统永磁电机,其反电势波形发生了严重的畸变,含有大量的偶次谐波。交替极永磁电机采用FLW-1和FLW-2绕组可以提高反电势波形质量,由图8(b)的谐波分析结果可看出:交替极永磁电机采用FLW-2绕组,其反电势2次谐波基本可忽略不计。但是FLW-2交替极永磁电机的反电势基波幅值相比传统永磁电机下降了3.28%,这主要因为FLW-2的两套绕组在空间上偏移了两个齿,电机基波绕组因数仅为0.888,反电势波形改善的同时牺牲了部分工作谐波,电机的转矩密度会略有下降。

图8 传统和CP PM 电机的反电势

4.2 转矩特性分析

采用交替极永磁转子会改变电机的齿槽转矩周期,对于交替极永磁电机,其转子旋转一周对应的齿槽转矩周期数[16]为

Ncog=LCM(Ns,P)。

式中:LCM表示最小公约数;Ns为定子槽数;P为转子极对数。传统和交替极永磁电机的齿槽转矩波形如图9所示,图中二者的齿槽转矩波形分别对应主要和次要纵坐标轴,电机旋转一周对应的齿槽转矩周期和齿槽转矩峰值如表3所示。由图9可知交替极永磁电机的齿槽转矩周期是传统永磁电机的两倍,同时交替极永磁电机的齿槽转矩峰值也比传统永磁电机大97 mN·m,交替极永磁电机齿槽转矩周期的翻倍导致其表现出较大的齿槽转矩。

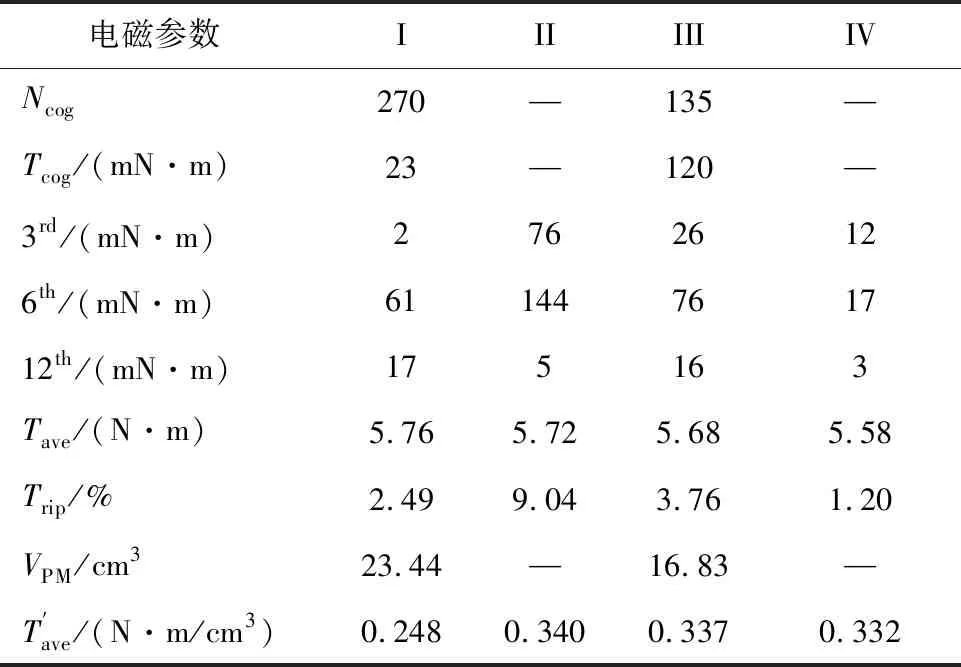
表3 永磁电机电磁特性和永磁体用量

图9 传统和CP PM电机的齿槽转矩

传统和交替极永磁电机的电磁转矩波形如图10所示,转矩特性和永磁体用量如表3所示。由图10可看出双层绕组交替极永磁电机的转矩脉动最大且含有较大的三次电磁转矩脉动;FLW-1交替极永磁电机与双层绕组交替极永磁电机相比,其转矩脉动可以下降5.28%,平均电磁转矩基本相等。虽然FLW-2交替极永磁电机的平均电磁转矩相比双层绕组交替极永磁电机下降了2.45%,但是其转矩脉动在四个电机中是最小的,仅有1.2%。交替极永磁电机与传统永磁电机相比可节约28.2%永磁材料;保证相同铜耗(PCu=15 W)时,双层绕组交替极永磁电机单位体积永磁体的转矩密度最大,但是其转矩脉动也是最大的,FLW-2交替极永磁电机单位体积永磁体的转矩密度相比双层绕组交替极永磁电机下降8 mN·m/cm3。

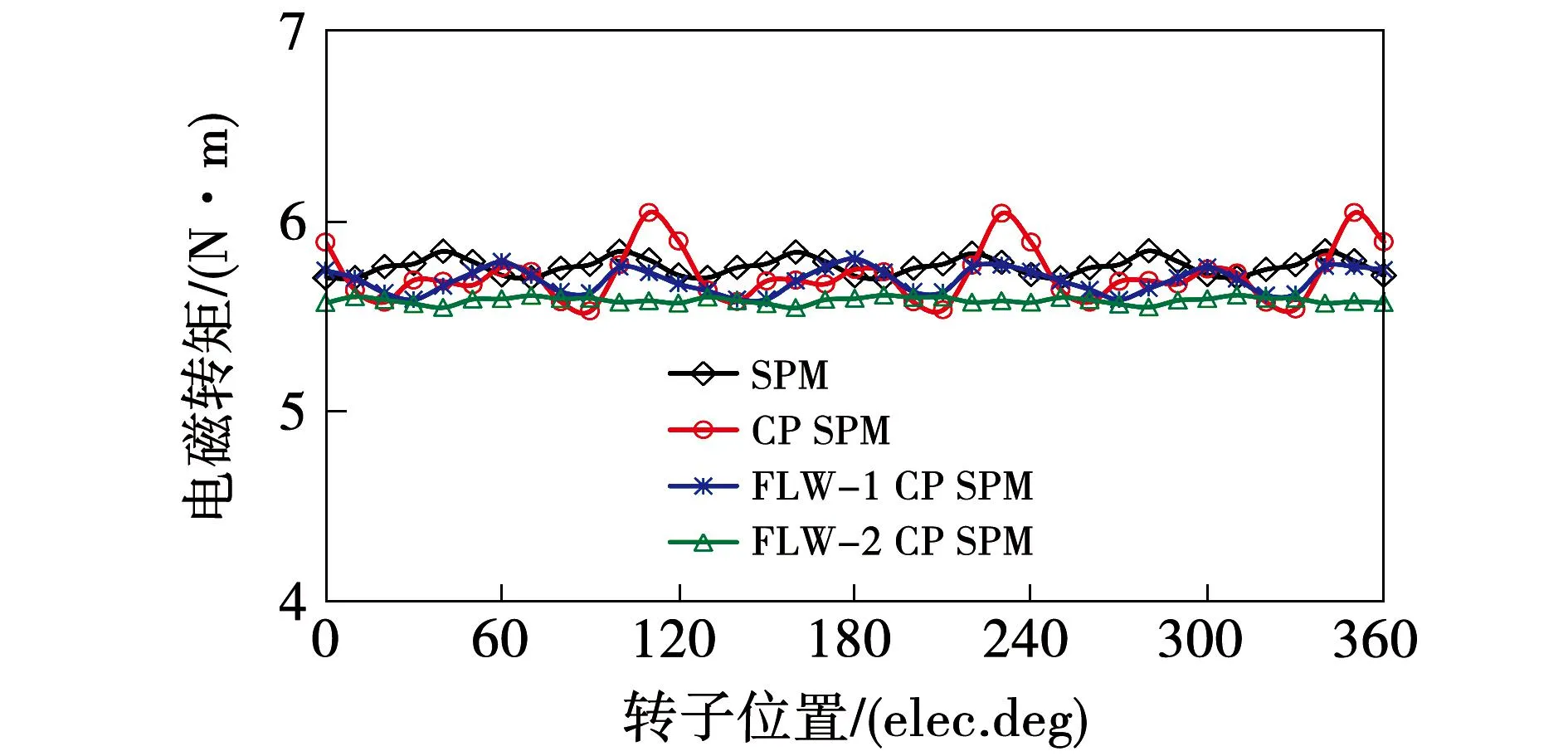
图10 传统和CP PM 电机的电磁转矩

传统和交替极永磁电机的平均电磁转矩随电流角的变化如图11所示,由图可知四个电机均在电流角为0时获得最大电磁转矩,磁阻转矩基本可忽略不计,并且不受绕组连接方式的影响。这表明无论是传统永磁电机还是交替极永磁电机,在恒转矩区均适合采用id=0控制策略实现最大转矩电流比控制。

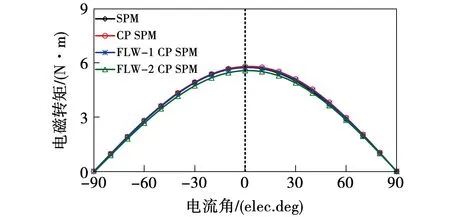
图11 电磁转矩随电流角的变化

5 实验验证

为了验证FLW-2绕组的反电势偶次谐波消除原理,以及交替极永磁电机的转矩特性,实验加工了一台FLW-2交替极永磁电机原理样机。电机的27槽定子和30极交替极永磁转子如图12(a)所示,电机的主要结构参数和线圈绕组匝数与表1和表2中参数保持一致。线圈绕制时每个定子齿上的线圈匝数需要严格按照表2中的参数,否则会影响偶次谐波消除效果。

图12 FLW-2 CP PM电机样机和静态转矩测试平台

图13给出了FLW-2交替极永磁电机的实测和有限元计算空载反电势波形,谐波分析结果如表4所示。由表4可看出FLW-2交替极永磁电机的反电势基波测试结果可达到仿真结果的91.96%,误差可能来源于电机加工、测试误差和交替极转子的端部效应[19]。FLW-2交替极永磁电机的反电势2次谐波测试与仿真结果基本吻合,验证了本文理论分析的正确性。

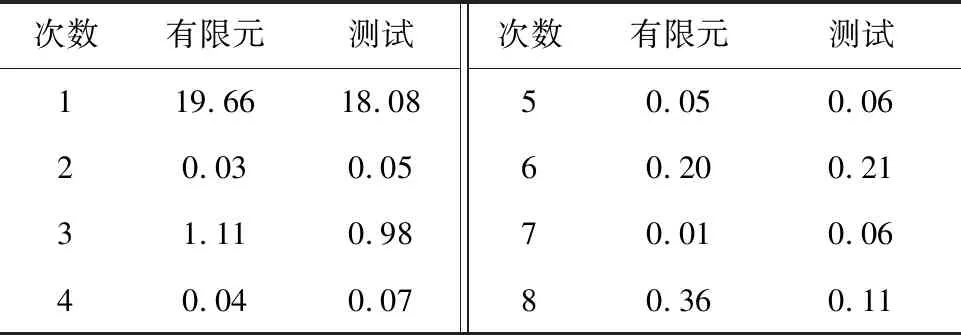
表4 测试和仿真的空载反电势谐波分析

图13 测试和仿真的空载反电势波形对比

为了验证交替极永磁电机的转矩特性,样机的齿槽转矩和静态电磁转矩在图12(b)的测试平台进行了测试。文献[20]详细介绍了内转子永磁电机的齿槽转矩测试方法,对于外转子永磁电机,齿槽转矩测试时电机内定子输出轴固定在旋转分度盘头上,测试臂杆通过不锈钢铁盘与电机外转子端部连接,测试臂杆的终端放置在电子秤上,转动分度盘手柄会带动电机内定子旋转,通过控制分度盘转过的角度可以控制电机定转子之间的相对位置,当定转子位置发生变化时可通过电子秤读数乘以力臂长得到电机的转矩。需要注意的是在测试过程中应保证力臂杆水平且不要人为触碰测试台架,因为样机的齿槽转矩在毫牛米级,力臂杆倾斜和人为触碰测试台架会导致测试结果不精确。

交替极永磁电机原理样机测试和仿真的齿槽转矩如图14所示。由于测试误差、电机加工精度和端部效应等原因,测试和仿真结果存在误差,但齿槽转矩周期基本吻合,与3.2节理论分析一致。交替极永磁电机原理样机的测试和仿真静态转矩随转子位置的变化如图15所示,静态转矩测试时,相绕组通入直流电,即IA=IB/cos(120°)=IC/cos(240°),测试和仿真结果基本吻合。

图14 测试和仿真的齿槽转矩对比

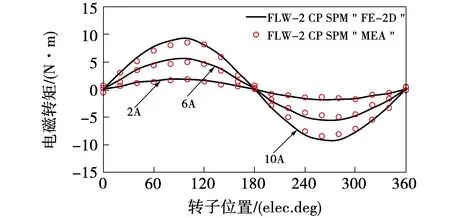
图15 测试和仿真的静态转矩对比

6 结 论

本文针对交替极永磁电机的反电势偶次谐波问题,提出了一种不等匝绕组结构(FLW-2),采用反电势星形图阐述了FLW-2的反电势偶次谐波消除原理,并根据理论计算的绕组匝数加工了一台样机。通过有限元软件分析了FLW-2交替极永磁电机的空载磁密特性、反电势特性和电磁转矩特性,并对样机进行了测试,验证了仿真结果,得到了以下结论:

1)对于FLW-2绕组,相邻3个定子齿上的单套绕组线圈匝数满足N2=2N1×0.742,N3=2N1×0.395时,可以消除交替极永磁电机的反电势2次和4次谐波,改善反电势波形质量,减小电机的电磁转矩脉动。

2)相同铜耗下,FLW-2绕组交替极永磁电机的转矩密度为传统交替极永磁电机的97.6%,但是其电磁转矩脉动仅为1.2%,比传统交替极永磁电机小7.84个百分点。