基于Wiener过程的电机主绝缘材料寿命预测方法
李贵衡, 张健, 黄少坡, 项石虎, 牛峰, 方攸同
(1.河北工业大学 河北省电磁场与电器可靠性重点实验室,天津 300401; 2.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300401; 3.浙江大学 电气工程学院,浙江 杭州 310027; 4.北京石油化工学院 信息工程学院,北京 102617)
0 引 言
电机是电力工业中的关键设备,其可靠性很大程度上取决于绝缘结构与绝缘材料性能。随着电机服役时间的增加,其在运行过程中承受的热应力、电应力、环境应力等会加速绝缘的不可逆退化,甚至造成电机故障,电机故障中有三成以上都是电机绝缘故障[1]。研究电机主绝缘材料退化过程,预测电机主绝缘材料寿命,对减少电机故障和提升电机可靠性具有重要意义。
目前,国内外大部分对于电机绝缘材料退化的研究均聚焦于借助局部放电量来判定绝缘材料的退化情况。文献[2]深入研究了绝缘材料表面电荷的运动过程,并描述了其内部的物理化学反应,得到了绝缘材料表面电荷数量与局部放电量之间的关系。文献[3]比较了不同电应力下绝缘材料局部放电量的变化规律,并建立了绝缘材料的剩余寿命预测模型,进而得到绝缘材料局部放电量与剩余寿命之间的关系。部分学者对电机主绝缘材料聚酰亚胺在高温下的性能进行了研究。文献[4]对不同类型的聚酰亚胺薄膜进行高温试验,并利用热重法分析了聚酰亚胺在高温下的动力学规律,得出聚酰亚胺具有良好热稳定性的结论。文献[5]采用两步合成法研究了聚酰亚胺的热稳定性,并利用热分析法探究了温度应力对聚酰亚胺热分解反应速率的影响,结果表明聚酰亚胺在高温下的热分解速率较低,即聚酰亚胺具有优越的耐热能力。
Wiener过程模型参数较少,预测精准度较高,因而被广泛用于各种设备和材料的退化建模[6-8]。文献[9]采用融入剩余寿命自适应预测方法的Wiener过程描述桥梁结构的退化过程,实现了桥梁结构剩余寿命的自适应预测。文献[10]提出了融入非线性漂移的Wiener过程模型,在模型表达式中加入标准布朗运动描述退化过程的随机性,并推导出相应的寿命概率密度函数与分布函数的数学表达式。文献[11]考虑了Wiener过程模型参数的随机性,假设不同样本的漂移参数服从正态分布,以此体现样本个体间的退化差异,使退化模型更符合工程实际。文献[12]和文献[13]建立了考虑退化过程中各种随机性的步进应力加速退化模型,提升了步进应力模型的预测精度。
本文在分析电机主绝缘材料退化机理的基础上,对电机主绝缘材料进行恒定温度应力加速退化试验,选用最大局部放电量作为电机主绝缘材料的退化特征量,建立基于Wiener过程的电机主绝缘材料退化模型并利用极大似然估计法得出模型中的未知参数,进而得到电机主绝缘材料在加速应力下的寿命分布与可靠度函数。最后利用高温下Wiener过程的参数估计值与加速退化试验数据建立Arrhenius模型,实现常温下电机主绝缘材料的寿命预测。本文为不同温度下电机主绝缘材料的寿命预测提供理论指导,提高电机主绝缘的可靠性。
1 加速退化试验
1.1 加速应力的选取
电机运行过程中,导致其主绝缘材料退化的最主要应力为热应力。高温使绝缘材料中电子的动能保持在高水平状态,且温度升高会加速绝缘材料中部分电子的激发,进而提高放电机率。同时,高温会使绝缘材料内部发生水解、氧化、裂化等化学反应,这些化学反应的速率决定着绝缘材料退化的速率[14]。所以绝缘材料的退化速率与温度应力关系密切,并且在实际加速退化试验中,温度应力相较其他应力更易于调控。因此,本文选择温度作为加速退化应力。
1.2 加速退化试验设计
聚酰亚胺长期使用温度范围为-200~300 ℃,选择略低于其长期最高工作温度的290 ℃为最低加速应力水平T1,应力水平T2设定为其长期工作的最高温度300 ℃,以此类推T3,T4分别设置为310、320 ℃。综合国家标准《恒定应力寿命试验和加速寿命试验方法总则》(GB 2689.1—1981)与试验成本等实际因素,制定出6050聚酰亚胺薄膜的加速退化试验方案:以0.25 mm的6050聚酰亚胺薄膜为试验对象,每个温度应力下随机抽取7个样本分别进行加速退化试验。以20 h为试验周期,每个温度应力下进行13个周期试验,每次试验周期结束后离线测试绝缘材料50 Hz下等效电容值、200 ℃下等效电阻值、交流800 V电压下最大局部放电量等数据。图1(a)为加速退化试验所用恒温恒湿试验箱。

图1 加速退化试验与绝缘电阻测试
参考国标《电气绝缘用薄膜第2部分:试验方法》(GB/T 13542.2—2009),绝缘电阻由具有温升功能的电阻率测试仪在200 ℃温度下测出,此设备基于欧姆定律,通过电压电流计算得出聚酰亚胺薄膜的绝缘电阻值。图1(b)为本文使用的电阻率测试仪。
参考国标《电气绝缘用薄膜第2部分:试验方法》(GB/T 13542.2—2009),绝缘电容由IDX300绝缘诊断系统在50 Hz频率下测出,此设备基于西林电桥平衡原理,通过式(1)得出聚酰亚胺薄膜的绝缘电容值。图2(a)为西林电桥原理图,图2(b)为本文使用的IDX300绝缘诊断系统,且有
(1)

图2 绝缘电容测试
参考国标《局部放电测量》(GB/T 7354—2003),本文采用耦合电容作为传感器测试工频800 V交流电下聚酰亚胺薄膜的局部放电,测试原理如图3(a)所示。图中:Cx为样本电容;Ck为耦合电容;Z为低通滤波器;Zm为测试阻抗。工频电压经Z滤波后施加于样本Cx,样本产生的局部放电脉冲经Ck耦合到Zm上,再经过放大器A输入测试仪器中。图3(b)为本文使用的局部放电测试系统。

图3 局部放电测试
1.3 加速退化试验数据
由于单个样本的退化具有随机性,所以采用7个样本等效电容值、等效电阻值、最大局部放电量三种指标在每个试验周期的平均值来代表当前时刻样本总体的绝缘参数水平,相关结果分别如图4、图5、图6所示。

图4 样本平均等效电容变化趋势
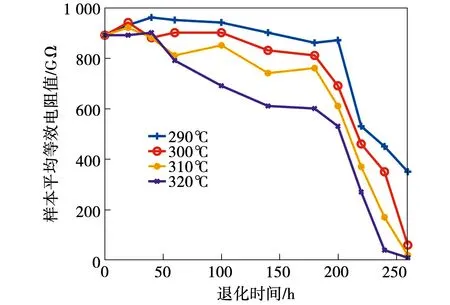
图5 样本平均等效电阻变化趋势

图6 样本平均最大局部放电量变化趋势
由图4可知,随着加速退化时间的增加,不同温度应力下样本平均等效电容均呈现上升趋势,样本平均等效电容在前180 h变化幅度较小,不同应力水平对样本平均等效电容的上升速度没有明显影响。由图5可知,随着加速退化时间的增加,不同温度应力下样本平均等效电阻均呈现下降趋势,样本平均等效电阻在前180 h变化幅度较小,应力水平的提升会加快样本平均等效电阻的下降速度。由图6可知,随着加速退化时间的增加,不同温度应力下样本平均最大局部放电量均呈现上升趋势,样本平均最大局部放电量在前180 h变化幅度较大,应力水平的提升会加快样本平均最大局部放电量的上升速度。
局部放电是电机主绝缘材料退化的最典型特征,也是反映主绝缘材料退化程度的重要指标。通过监测最大局部放电量既可以识别主绝缘材料放电的位置,还可以辨识放电的类型。由于局部放电强度在绝缘材料失效前有微弱下降,且本文利用首达时概念判定绝缘材料失效,故得到的预测寿命稍小。利用首达时判定失效可以滤除局部放电强度的非线性部分,又保证了电机主绝缘的高可靠性。通过理论分析和试验数据分析,本文选择能反映主绝缘材料状态、变化趋势明显、与应力水平强关联的最大局部放电量作为电机主绝缘材料的退化特征量。图7为不同温度下所有样本最大局部放电量变化趋势,由图可知,同一温度下不同样本的最大局部放电量存在差异,且此差异随着温度上升而增大。
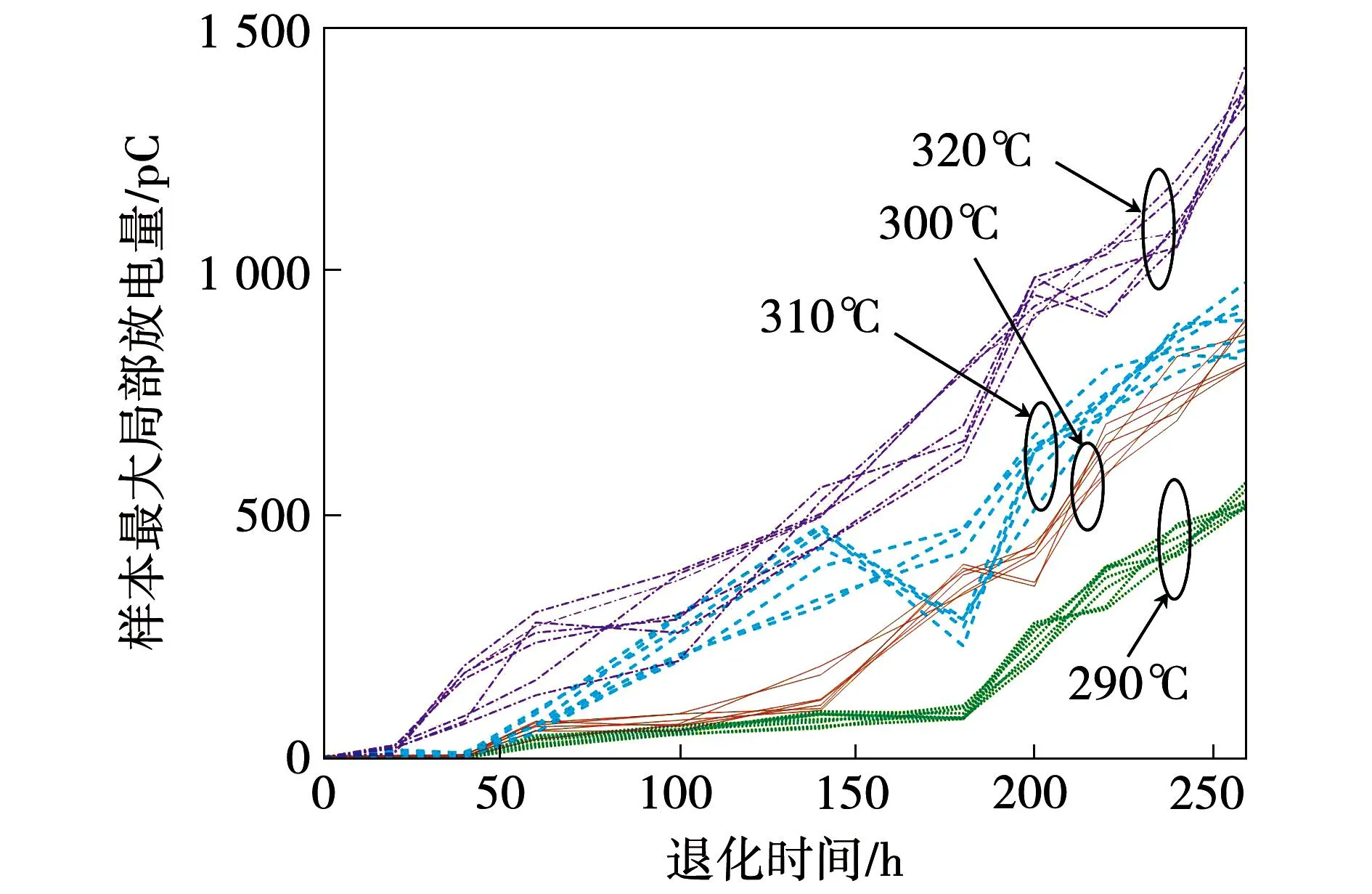
图7 所有样本最大局部放电量变化趋势
2 电机主绝缘材料退化建模
2.1 退化模型的选取
如果材料的退化由大量微小损失累积导致,则可以考虑采用一元Wiener过程建模[15]。电机绝缘材料的内部结构长期受到热、电应力的侵蚀,其退化由大量微小损失累积导致[16],符合Wiener过程的特征。Wiener过程中的布朗运动可将绝缘材料在制造、运行过程中的随机性与偶然性融入模型中。因此,本文选取能够反映累积性和随机性退化的基于Wiener过程的模型作为电机主绝缘的退化模型。
如果利用一元Wiener过程进行退化建模,则退化特征量X(t)需满足以下条件:
1)在任意时间段[t,t+Δt]内的增量服从正态分布,即X(t+Δt)-X(t)~N(μΔt,σ2Δt);
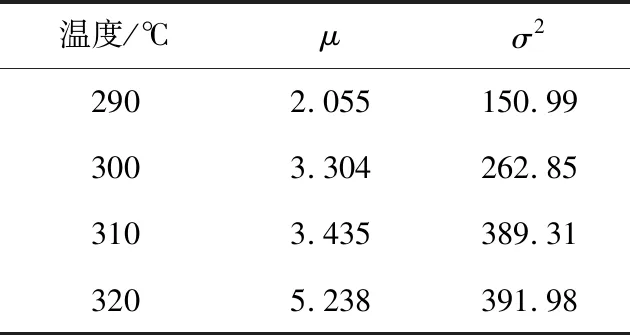
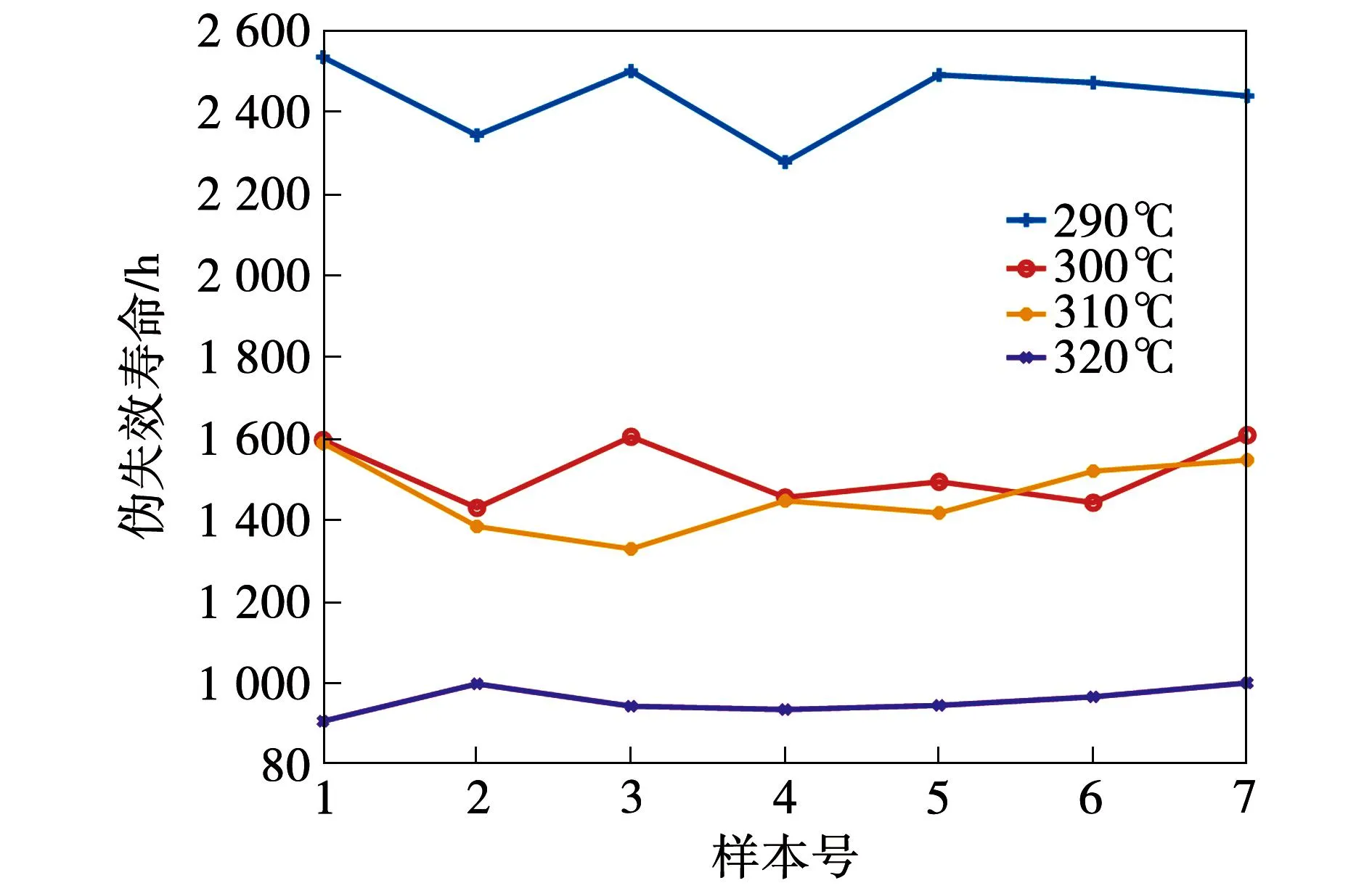
2)在退化过程中任意两个不相交的时间段[t1,t2],[t3,t4],t1 3)P(X(0)=0)=1。 本文选择电机主绝缘最大局部放电量为退化特征量,Wiener过程模型为退化模型,在退化建模前需对最大局部放电量分段退化量进行正态检验。 图8为320 ℃下7个样本的最大局部放电量分段退化量分布图。 图8 最大局部放电量分段退化量分布 由图8可以看出,320 ℃下最大局部放电量分段退化量主要集中在[0,200]pC区间内,其分布近似呈正态分布。利用Kolmogorov-Smirnov(KS)法对最大局部放电量分段退化量进行正态检验。构造检验统计量 f=max(|F(x)-G(x)|)。 (2) 其中:F(x)为样本分布函数;G(x)为目标分布函数。检验统计量f是样本总体分布与给定分布之间距离的最大值。显然,当两分布F(x)与G(x)相近的时候,f较小。计算出f后与指定的临界值n作比较,若f≥n则拒绝原假设,反之接收原假设。设显著性水平n=0.05,分别对320 ℃和其余三个温度应力下的分段退化量分别进行KS检验,均得到H=0,因此接受原假设,可以认为最大局部放电量分段退化量服从正态分布。故可以利用Wiener过程描述电机主绝缘材料的退化过程,进而预测主绝缘材料寿命。 以最大局部放电量作为电机主绝缘材料的退化特征量,考虑退化过程中的随机因素,建立带漂移的一元线性Wiener过程模型 X(t)=μt+σB(t)。 (3) 其中:t为退化时间;μ为漂移参数,反映了退化特征量的变化速度;σ为扩散参数,反映了测量误差、噪声等随机因素对退化的影响。B(t)为标准布朗运动;X(t)为t时刻最大局部放电量的累积退化量,且X(t)~N(μt,σ2t),X(t)的期望与方差为时间的线性函数。利用极大似然估计和加速退化试验数据对μ,σ进行估计,设xij为第i个样本在第j个周期的分段退化量,i=1,2,…,n,j=1,2,…,m,且xij~N(μΔt,σ2Δt),Δt为周期间隔。极大似然函数如下: (4) 对数似然函数为 lnL(μ,σ2)= (5) 由式(5)可以得到参数μ,σ2的极大似然估计为: (6) 由给定失效阈值L,直接定义寿命T={t|X(t)≥L},对应的寿命分布函数定义为 FT(t)=P(T≤t)=P(X(t)≥L)。 (7) 寿命概率密度函数与寿命分布函数为: (8) 进而得到可靠度函数 (9) 其中Φ为标准正态分布的分布函数。 工程实际中为了降低失效风险,寿命T定义为累积退化量X(t)首次超过失效阈值L的时刻,这个时刻被称为首达时。此时寿命T的定义为T=inf{t|X(t)≥L},寿命T的概率密度函数与分布函数不再是式(8)。通过首达时定义的寿命概率密度函数与寿命分布函数如下: (10) (11) 对应的可靠度函数 (12) 进而得出寿命T的期望和方差 (13) 以不同温度应力下的试验样本为分析对象,利用加速退化试验数据可以得到电机主绝缘材料退化模型中未知参数μ、σ2的估计值,如表1所示。 表1 加速应力下的参数估计值 参考波兰波兹南电力工程研究所局部放电标准[17],设失效阈值L=5 000 pC。利用表1中的4组参数估计和式(10)、式(12)得到电机主绝缘材料寿命概率密度曲线和可靠度曲线,分别如图9、图10所示。 图9 高温下寿命概率密度 图10 电机主绝缘材料可靠度 从图9可以看出,4种温度应力水平下电机主绝缘材料的寿命概率密度分布均近似正态分布。随着温度应力提升,电机主绝缘材料的寿命概率密度曲线左移,即整体寿命降低,同时电机主绝缘材料的寿命分布逐渐向期望寿命E[T]集中。 从图10可以看出,在290 ℃温度应力下,当退化时间达到2 000 h左右,电机主绝缘材料的可靠度开始明显降低。当退化时间达到3 200 h时,电机主绝缘材料的可靠度降为0。随着温度应力的提升,电机主绝缘材料可靠度开始明显下降的时间提前,且可靠度下降速度提升。在320 ℃温度应力下,当退化时间达到700 h左右,电机主绝缘材料的可靠度开始明显降低,下降速度明显高于前三种温度应力。当退化时间达到1 200 h时,电机主绝缘材料的可靠度降为0。 在电机主绝缘材料寿命区间估计的基础上进行电机主绝缘材料寿命点估计。本文将电机主绝缘材料的伪失效寿命定义为期望寿命E[T]。令式(6)中n=1,对不同温度应力下单个样本的退化模型进行参数估计,得出单个样本的期望寿命E[T],进而得到不同温度应力下单个样本的伪失效寿命,如图11所示。 图11 电机主绝缘材料伪失效寿命 从图11可以看出,同一温度应力下不同样本的伪失效寿命差异很小,样本伪失效寿命随着温度应力提升而大幅降低。 建立Wiener过程模型未知参数与温度应力的Arrhenius模型,利用加速退化试验数据和极大似然估计法外推出常温下电机主绝缘材料的伪失效寿命。Arrhenius模型描述了模型参数与温度应力之间的关系,被广泛应用于各类产品的加速退化试验数据分析,其公式如下: (14) 其中:y为模型中的参数;Tk为绝对温度;b为玻尔兹曼常数;Ea为激活能。为了便于计算,需将指数形式的Arrhenius模型线性化。对式(14)两侧取对数,可得 lny=c1+c2φ(Tk)。 (15) 其中c1=lna,c2=-Ea/b,Φ(t)=1/Tk。经过以上化简,温度Tk下的Wiener过程参数可以表示为: (16) (17) 不同温度下寿命的概率密度函数和可靠度函数为: (18) 利用最小二乘法和表1中的四组参数数据,可以估计出c1、c2、c3的初始值。设xijk为第k个温度应力下第i个样本在第j个周期的分段退化量,i=1,2,…,n,j=1,2…,m,k=1,2,3,4,由Wiener过程的性质可知xijk~N(exp(c1+c2/Tk)Δt,exp(2c3+c2/Tk)Δt),其中Δt为周期时长,则由加速退化试验数据得到的极大似然函数为 (19) 对式(19)取对数后分别对3个未知参数求偏导,并令偏导数为0。代入加速退化试验数据,可以求得c1=17.74,c2=-9 553,c3=11.34。对常温下电机主绝缘材料的寿命进行预测,需估计出常温下Wiener过程模型的未知参数。设常温为50~80 ℃,绕组温升为125 ℃,则电机主绝缘材料的性能参考温度为175~205 ℃,利用式(17)可以得到常温下的模型参数值如表2所示。 表2 常温下的参数估计值 根据表2中的数据和式(10)得到常温下电机主绝缘材料的寿命概率密度分布,如图12所示。 图12 常温下寿命概率密度 从图12可以得出常温下电机主绝缘材料的最大寿命、最小寿命。将表2的参数估计值代入式(13)可以得到常温下电机主绝缘材料的伪失效寿命,如表3所示。 表3 常温下的寿命预测 由图12和表3可以看出常温下电机主绝缘材料的伪失效寿命随温度升高而降低。由于电机主绝缘系统是电机的脆弱环节,主绝缘材料寿命的长短很大程度上决定了电机的寿命,需保证电机主绝缘材料的高可靠性。 本文提出的基于Wiener过程的电机主绝缘材料寿命预测方法和得出的相应预测结果可以为电机主绝缘状态评估与安全运维提供参考,主绝缘的状态评估与寿命预测相结合可以更准确地预测主绝缘的退化趋势,有助于检修人员制定科学合理的绝缘运维计划。 本文对电机主绝缘材料进行恒定温度应力加速退化试验,利用加速退化试验数据建立了基于Wiener过程的电机主绝缘材料退化模型,结合Arrhenius模型外推出常温下电机主绝缘材料的伪失效寿命,开展的主要工作和得到的结论如下:根据加速退化试验数据得出温度升高增加了电机主绝缘材料的最大局部放电量,即温度升高加速了电机主绝缘材料的退化;利用Kolmogorov-Smirnov方法验证了最大局部放电量分段退化量服从正态分布,符合Wiener过程的使用条件,进而利用加速退化试验数据和极大似然估计法,得出Wiener过程模型和Arrhenius模型未知参数的估计值,预测出加速应力和常应力下电机主绝缘材料的伪失效寿命。相关研究结论能够对电机可靠性提升进行支撑。2.2 最大局部放电量分段退化量分布特征

2.3 电机主绝缘材料退化模型
3 电机主绝缘材料寿命预测
3.1 加速应力下电机主绝缘材料的寿命预测


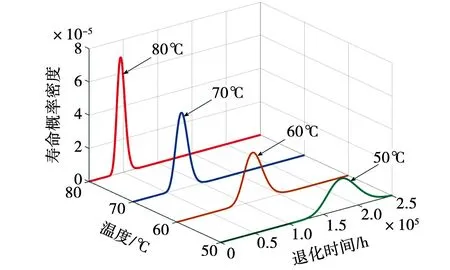
3.2 常温下电机主绝缘材料的寿命预测



4 结 论

