基于调制波分解的中点钳位型三电平逆变器的混合调制策略

王金平, 吉耀聪, 张庆岩, 刘圣宇, 姜卫东

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

0 引 言

中点钳位型三电平逆变器(neutral point clamped three-level inverter,NPC TLI)是在高功率场合下应用最为广泛的多电平逆变器之一,其具有总谐波失真低、开关器件电压应力低和转换效率高等优点。在光伏并网、交流电机调速和电能质量综合治理等领域,NPC TLI都发挥着重要的作用[1-5]。

中点电压(neutral point voltage,NPV)平衡是研究NPC TLI的关键问题[6]。在实际应用中,由于上下电容不一致或电容器充放电速率不对称,NPV会产生一定的波动,包括直流分量和交流分量两部分。这会导致功率器件的电压应力升高,滤波电感产生低频电流谐波,以及母线电容器的使用寿命降低等一系列问题,系统的可靠性将大大降低[7]。在直流侧采用大电容能抑制中点波动,但系统体积会增大。要维持NPV平衡,可在直流侧电容并联独立的直流电压源,这无疑增加了成本[8]。为了提高功率密度和降低成本,基于软件的解决方案更具有优势。

多年来,人们对调制策略进行了广泛的研究。现今主要通过各种脉冲宽度调制(pulse width modulation,PWM)策略维持NPV平衡,主要可以划分为载波脉宽调制(carrier based PWM, CBPWM)和空间矢量脉宽调制(space vector PWM,SVPWM),且二者具有等效性[9-11]。由于实现简便,CBPWM策略在工业应用中比SVPWM策略更受欢迎[12]。CBPWM策略有单调制波双载波和双调制波单载波两种方式,传统的单调制波双载波方式所生成的开关序列仅能同时产生0、1或1、2两个电平,而双调制波单载波方式可生成的开关序列能同时产生0、1、2三个电平。通过对双调制波的多种约束能实现不同的调制策略。传统的CBPWM不能在全功率因数和全调制度范围内实现NPV的平衡,在高调制度低功率因数的情况下,NPV会产生低频波动。文献[13]提出虚拟空间矢量PWM(virtual space vector PWM, VSVPWM)的方法,该方法用冗余小矢量控制NPV的偏移,能无条件实现NPV平衡,但会增加功率管的开关次数,且算法比较复杂。由于上、下电容不相等,死区时间等非理想因素的影响,各种调制策略下的NPV还可能会缓慢变化。因此,有必要加以NPV主动控制。在文献[14-18]中,NPV主动控制是通过给三相同时注入合适的零序电压(zero sequence voltage,ZSV)来实现,这可使流入或者流出中点的电流减小甚至达到0,从而平衡NPV。

NPC TLI还有一个重要的研究问题是开关损耗,低的开关损耗可以使NPC TLI运行效率提升,同时还能降低冷却系统的成本[19]。开关次数和导通电流是开关损耗最主要的2个影响因素。VSVPWM由于在一个周期内有4次开关动作,会大大增加开关损耗。相对VSVPWM,传统的CBPWM在一个周期内有3次开关动作,故开关损耗更小。

在文献[20]和文献[21]中,通过三相各电平占空比的计算获取双调制波,该方法未知变量多,计算过程繁琐。本文对调制波分解后的双调制波进行多种约束,更简便地获取双调制波,从而实现不同的调制策略。基于简单的调制波分解算法,提出一种混合调制策略,保证NPV在全调制度、全功率因数范围内平衡的同时,不过分增大开关损耗。

1 NPC TLI

NPC TLI的拓扑如图1所示,每一相由4个开关器件和2个钳位二极管组成。C1和C2为上、下电容。直流母线电压uDC为上下电容电压之和。电容电压均衡时,uC1=uC2=uDC/2。选择电容中点作为参考点。导通的开关器件和输出电平之间的关系见表1。

图1 NPC TLI拓扑

表1 导通的开关管与输出电平之间的关系

在稳态时,NPC TLI输出的三相电压ux(x=a,b,c)和电流ix可以表示为:

(1)

(2)

其中:ωt为相电压的相位角,m∈[0,1.154 7]为调制度;Im为相电流的峰值;φ为功率因数角。

NPC TLI一般采用空间矢量调制或载波调制。已有很多文献表明,这两种调制方法是等效的。CBPWM通过调制波与载波比较生成相应的PWM序列。与其它PWM调制策略相比,CBPWM更容易实现。

CBPWM一般使用三角载波,现在较常用的是用单调制波和双载波比较生成相应的PWM序列,如图2所示。图中:Sout,x是某一相输出的PWM序列;carrier1是上载波;carrier2是下载波。调制函数如下:

(3)

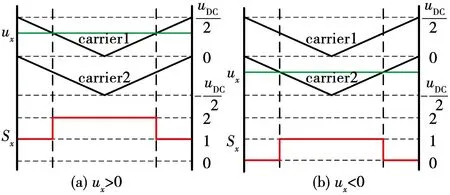
图2 双载波单调制波方式下生成的PWM序列

可以看出,在一个开关周期内,这种比较方式可确保每相输出电平0、1或1、2,使得每相发生2次开关动作。

2 调制波分解算法

为了便于分析和简化计算,对NPC TLI输出的三相电压ua、ub、uc排序:

(4)

式中:umax、umid、umin分别为最大电压、中间电压和最小电压;imax、imid、imin分别为它们对应的相电流。

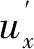
(5)

式中uZSV为向三相同时注入的ZSV。

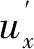
(6)

图3 调制波分解

根据文献[22],将一个调制波分解为2个调制波后,线电压可计算为:

(7)

可知,输出序列没有改变线电压关系。

事实上,式(5)仅给出了含有参数uZSV的3个方程,不足以确定每相的双调制波。每相的双调制波的求解还需要其他的附加方程。

众所周知,NPC TLI要尽量维持电容电压平衡。其基本原则是,若在一个开关周期起始时刻电容电压均衡,在该开关周期的结束时刻电容电压仍应维持平衡。三相电流在一个开关周期内注入中点的电流之和为i0,即

i0=imaxdmax,1+imiddmid,1+imindmin,1。

(8)

假设一个开关周期内三相电流近似不变,NPV不变的条件是在一个开关周期内注入中点的电流之和为0,即i0=0。此时,代入式(6)给出的占空比,式(8)可以改写为

(9)

2.1 开关次数的约束

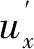
(10)

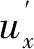
(11)

将式(11)代入式(5)中可知:

(12)

将式(11)和式(12)代入式(9)中,可以解得ZSV为

(13)

综合式(11)、式(12)和式(13),可知分解后的6个调制波为:

(14)

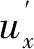
(15)

类比情形1,可算得此情形下ZSV为

(16)

同理,分解后的6个调制波为:

(17)

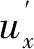
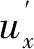
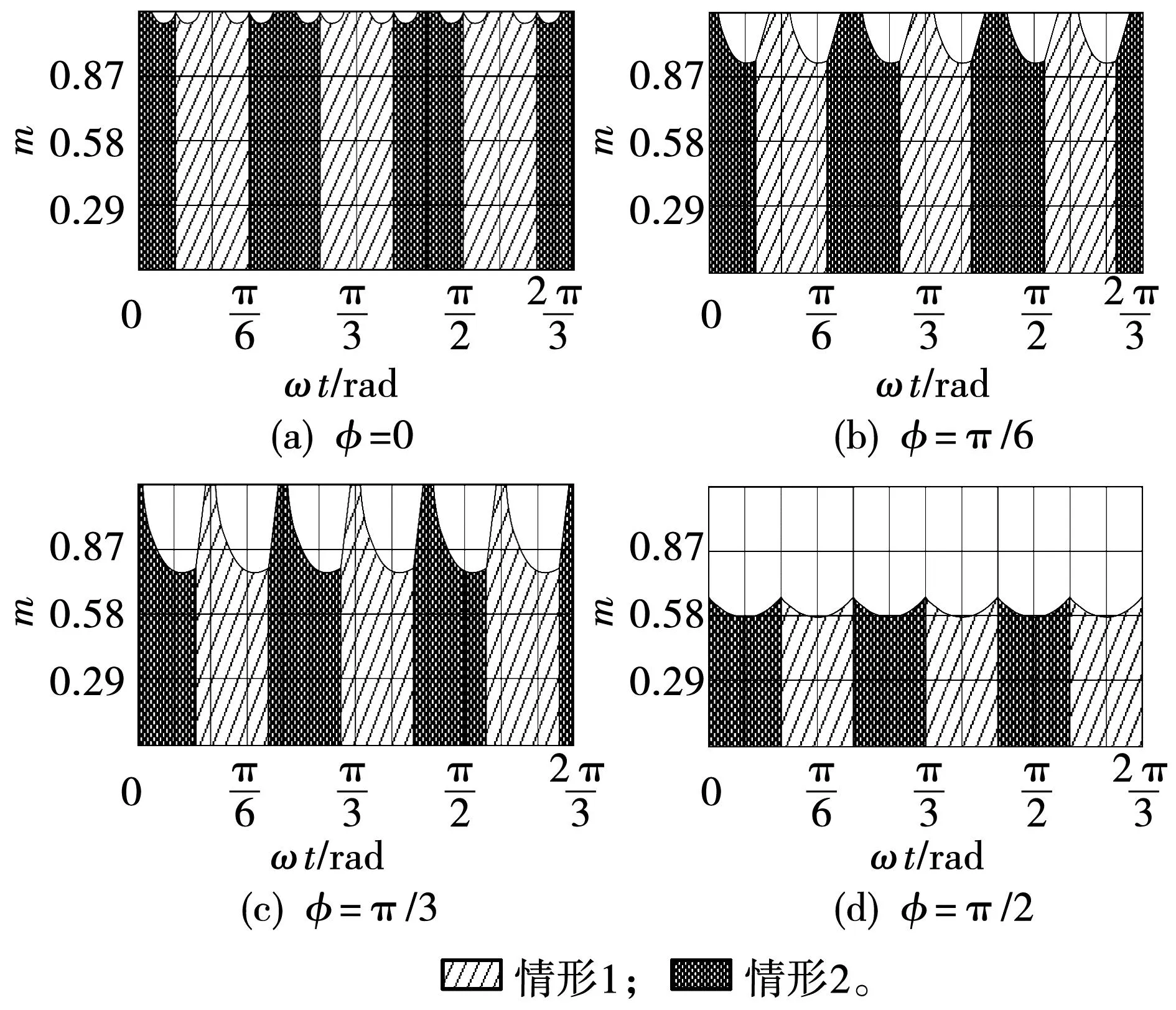
图4 不同功率因数下的可平衡区域

在基于开关次数的约束下,情形1与情形2以π/3为周期交替切换。当功率因数角φ=0时,除了调制度非常接近1.154 7的很小区域外,其余区域都使NPV在一个开关周期内平衡。随着功率因数的降低,情形1与情形2的适用区域逐渐变小。当功率因数角φ=π/2时,情形1与情形2的适用区域仅在调制度为0.58以下。

2.2 NPV无条件平衡约束

为了达到NPV的全功率因数范围平衡,应放宽对双调制波的约束。仅约束umax和umin：

(18)

则式(9)可以改写为

(19)

考虑到imax+imid+imin=0,则当下述条件成立时,即可使式(19)被满足

(20)

结合式(5)和式(20),求解出三相的双调制波为:

(21)

图5给出了NPV无条件平衡约束的实现方法。每相双调制波与同一载波比较后生成2个PWM子序列,将这2个PWM子序列相加得到每一相最终的PWM序列。可以看出,在NPV无条件平衡约束下,最大相的PWM序列由电平1、2组成,中间相的PWM序列由电平0、1、2组成,最小相的PWM序列由电平0、1组成。相比开关次数的约束,NPV无条件平衡约束在一个周期内的开关次数增加了一次,增大了开关损耗。

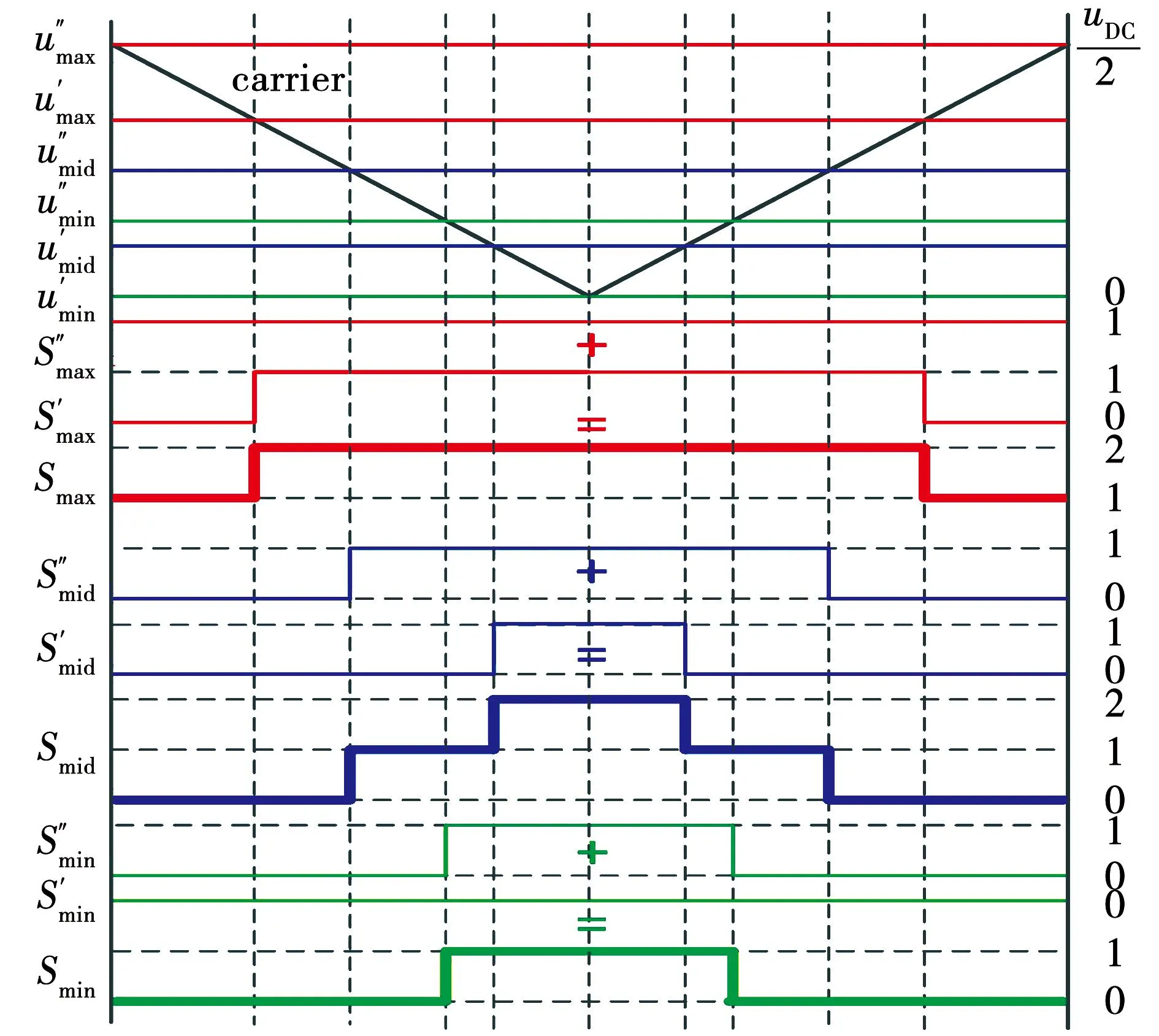
图5 调制波分解的开关序列

2.3 两种约束的混合调制策略

在基于开关次数的约束下,并非所有功率因数下都可以实现NPV在一个开关周期内平衡,而在NPV无条件平衡约束下,又会增大开关次数,从而增加开关损耗。因此,可以采用2种约束的混合调制策略,保证NPV在一个开关周期内平衡的前提下尽可能减小开关损耗。在图4中,与开关次数的约束适用区域互补,空白区域即为NPV无条件平衡约束的适用区域。

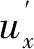
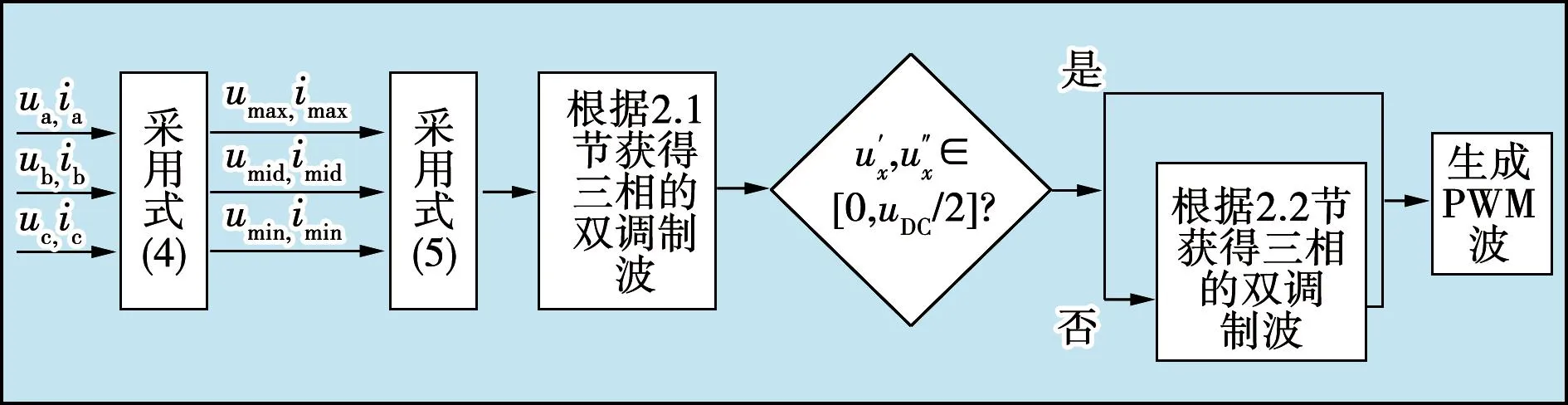
图6 混合调制策略的流程图

图7给出了基于开关次数的约束在混合调制策略中的占比情况。可以看出,低调制度下(m<0.58)可以全部采用基于开关次数的约束。而调制度较高(m>0.58)时,基于开关次数的约束在混合调制策略中的占比会随着功率因数的变化而剧烈变化。当功率因数大于0.866且m<0.928,就可以使开关次数的约束占比达到100%。当功率因数降低到0时,混合调制策略中,开关次数的约束占比将迅速降为0。

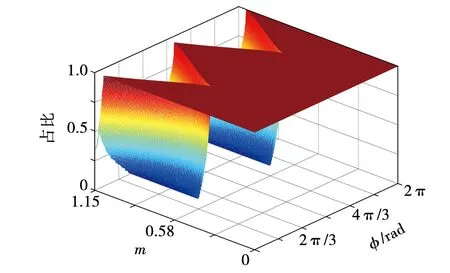
图7 开关次数的约束在混合调制策略中的占比情况

3 NPV主动控制方法

在基于开关次数的约束下,利用式(14)和式(17)计算双调制波时,需要用到下一开关周期的三相电流,而此电流还是未知的,如果用上一开关周期的三相电流替代,则不可避免的带来误差,导致NPV逐渐偏移。在NPV无条件平衡约束下,双调制波的计算虽然与三相电流无关。但一些非理想因素,例如电容容值的微小偏差、初始状态下的电容电压偏差、死区的插入等,都可能导致NPV逐渐偏移。

如果对NPV偏移不加以主动控制,可能使电容电压或功率器件的电压应力超过其允许值,导致装备保护或发生较为严重的故障。因此有必要探讨这两种约束下的NPV主动控制方法。

若检测到上下电容电压偏差ΔuNP=uC2-uC1。要改变NPV,必须向中点注入或抽取电流。NPV主动控制的关键就在于对中点电流的控制。为了使NPV重新回复至平衡状态,一个载波周期内需要向中点抽取的平均电流为

i0=ΔuNP(C1+C2)/TS。

(22)

式中TS为开关周期。代入式(6)给出的占空比,式(8)可以改写为

(23)

3.1 基于开关次数约束下的NPV主动控制

对于基于开关次数约束而言,三相的双调制波每相都有一个调制波为0或uDC/2,另一个调制波是随输出电压而改变。通过对后者注入ZSV实现NPV主动控制。

(24)

将式(24)代入式(23)可得

(25)

值得注意的是,ZSV由两部分组成,第一部分是为了在基于开关次数约束下实现NPV在一个开关周期平衡所注入的ZSV,等同于式(13)计算的 ZSV;第二部分是为了消除NPV偏移而注入的ZSV。

类似情形1,在基于开关次数约束下的情形2,实现一个开关周期内NPV平衡且消除偏移的ZSV为

(26)

3.2 NPV无条件平衡约束下的NPV主动控制

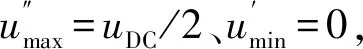
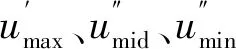
(27)

将式(27)代入式(23)可得

(28)

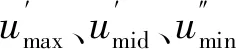
(29)

将式(29)代入式(23)可得

(30)

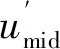
(31)

式中udmv为差模电压。

将式(31)代入式(23)可得

(32)

值得注意的是,NPV无条件平衡约束下所得的ZSV或差模电压只包含为了消除NPV偏移的部分。以上3种情形的调节能力有所不同,在实际应用中可以选择调节能力最强的一种[20]。

4 性能分析

本节主要从开关损耗方面评价本文提出的混合调制策略,并与现有的方法对比。

不同PWM策略下的导通损耗大致相等,但开关损耗相差很大。因此,在分析不同调制策略的损耗时,开关损耗占主导地位,不考虑传导损耗。

为了比较全调制度和全功率因数范围内的开关损耗,在不同调制度下,调节负载使相电流幅值保持不变。这样,开关损耗仅与调制方案、负载功率因数和调制算法的开关次数有关。由文献[23]知,在一个基波周期内,下式用于评估开关损耗,即

ic(n)kc(n)]。

(22)

在全调制度和全功率因数范围内,分别计算混合调制策略、CBPWM和VSVPWM在一个基波周期内的总开关损耗,分别命名为PHyb、PCB和PVSV。值得注意的是,在比较不同调制算法的开关损耗时,它们之间的比率比具体值更重要。

图8分别给出了PVSV/PCB、PHyb/PCB和PHyb/PVSV的值。从图8(a)可以看出,VSVPWM的开关损耗在全调制度和全功率因数范围内始终高于CBPWM。当φ=π/2和3π/2时,VSVPWM的开关损耗可以达到CBPWM的1.5倍左右。原因是umid对应的相电流最大,且该相有两次开关动作,开关损耗大大增加。当φ=0和π时,VSVPWM的开关损耗仍达到CBPWM的1.1倍左右。较高的开关损耗是VSVPWM的主要缺点。

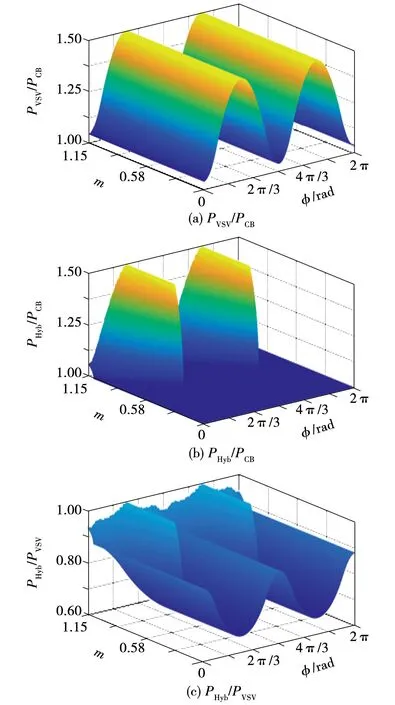
图8 不同调制策略下的开关损耗

图8(b)给出了PHyb/PCB在全调制度和全功率因数范围内的值。可以看出,当调制较低时(m<0.58),PHyb/PCB始终为1,即开关损耗与CBPWM相同。当调制较高时(m>0.58),开关损耗会随着功率因数的降低而增加。这是因为随着功率因数的降低,NPV无条件平衡约束比例逐渐增加,因此开关损耗增加。当功率因数为0时,即φ=π/2和3π/2,PHyb/PCB的值最高,可达1.5。这是因为几乎整个开关周期内都采用NPV无条件平衡约束。

图8(c)给出了全调制度和全功率因数范围内的PHyb/PVSV值。可以看出,PHyb/PVSV的值在全范围内都小于l。说明混合调制策略与VSVPWM相比,不仅可以平衡全范围内的NPV,而且可以降低开关损耗。

5 实验结果

为了验证本文提出的混合调制算法,搭建了NPC TLI的实验平台,其中交流源通过不控整流桥为逆变器提供直流侧电压,如图9所示。实验系统的主要参数见表2。本文实验部分分析了CBPWM、VSVPWM和混合调制策略。实验包括稳态实验和动态实验2个部分,并分析了实验结果。

表2 实验参数

5.1 稳态实验

图10～图12给出了CBPWM、VSVPWM和本文提出的混合调制策略在不同调制度和负载下的稳态实验结果,包括直流侧上下电容电压、双调制波、相电压相电流和线电压。在此次实验中,使用表2中的负载1～负载4来保持相电流的幅值不变。

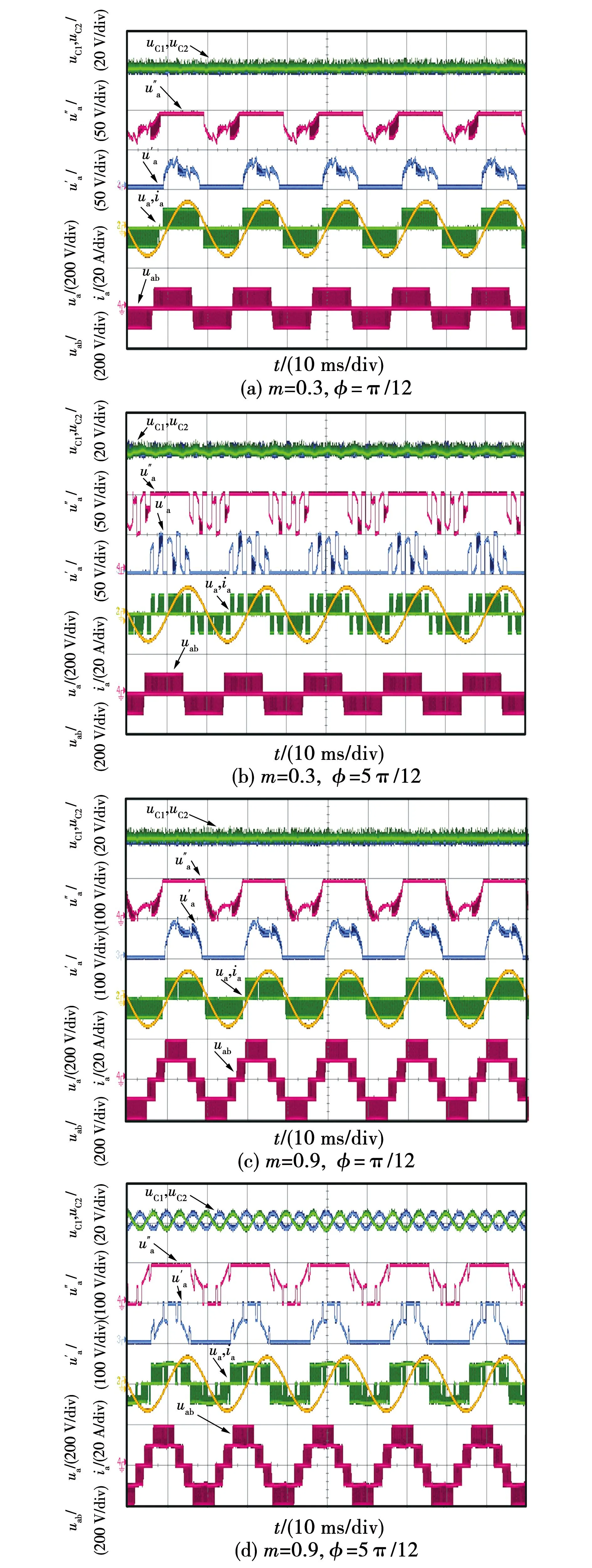
图10 CBPWM的稳态实验

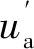
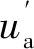
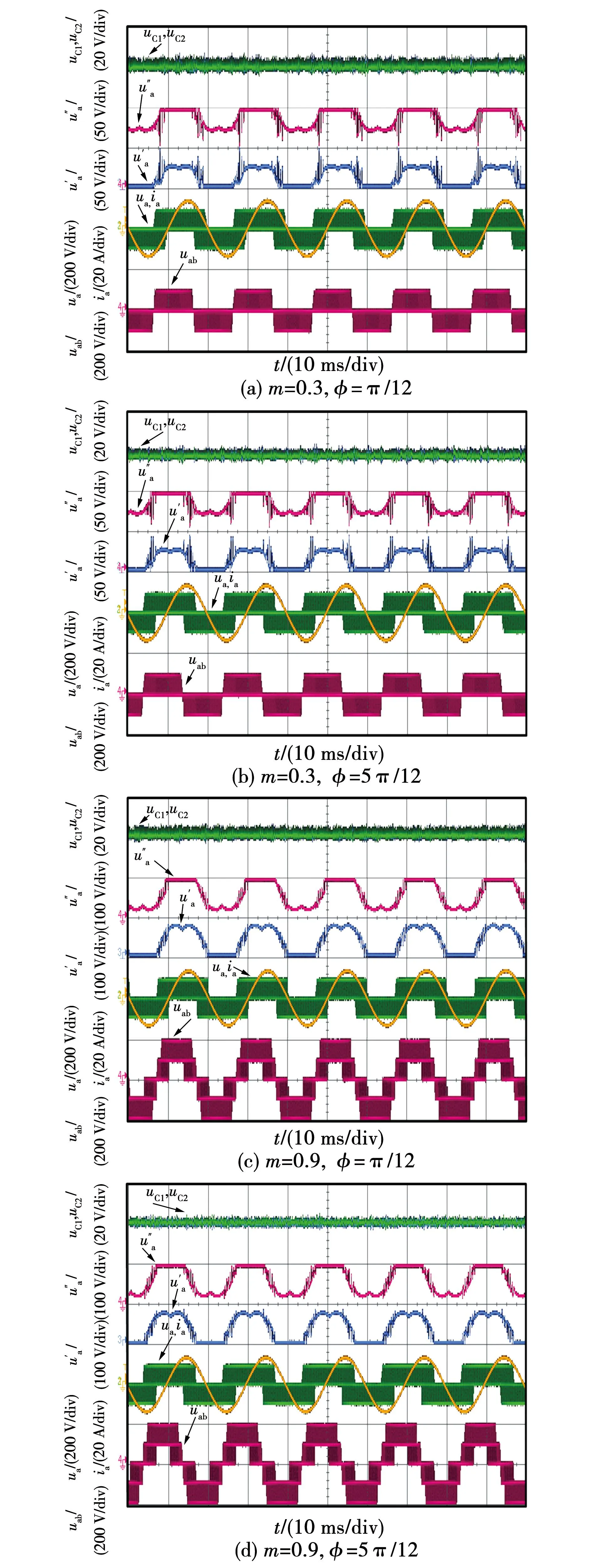
图11 VSVPWM的稳态实验

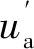
对于开关损耗,在实验中使用Tektronix TPS2024示波器与专业功率分析模块测量。图13给出了不同调制策略下的开关损耗测量值。图10～图12的4种工况分别表示为(a)～(d)。不难发现,CBPWM和VSVPWM的开关损耗分别为最低和最高,混合调制策略的开关损耗总是介于二者之间。实验研究中各种调制策略在不同情况下的开关损耗之比与图8中的仿真分析基本吻合。结果证明,相比于VSVPWM,混合调制策略有降低开关损耗的效果。

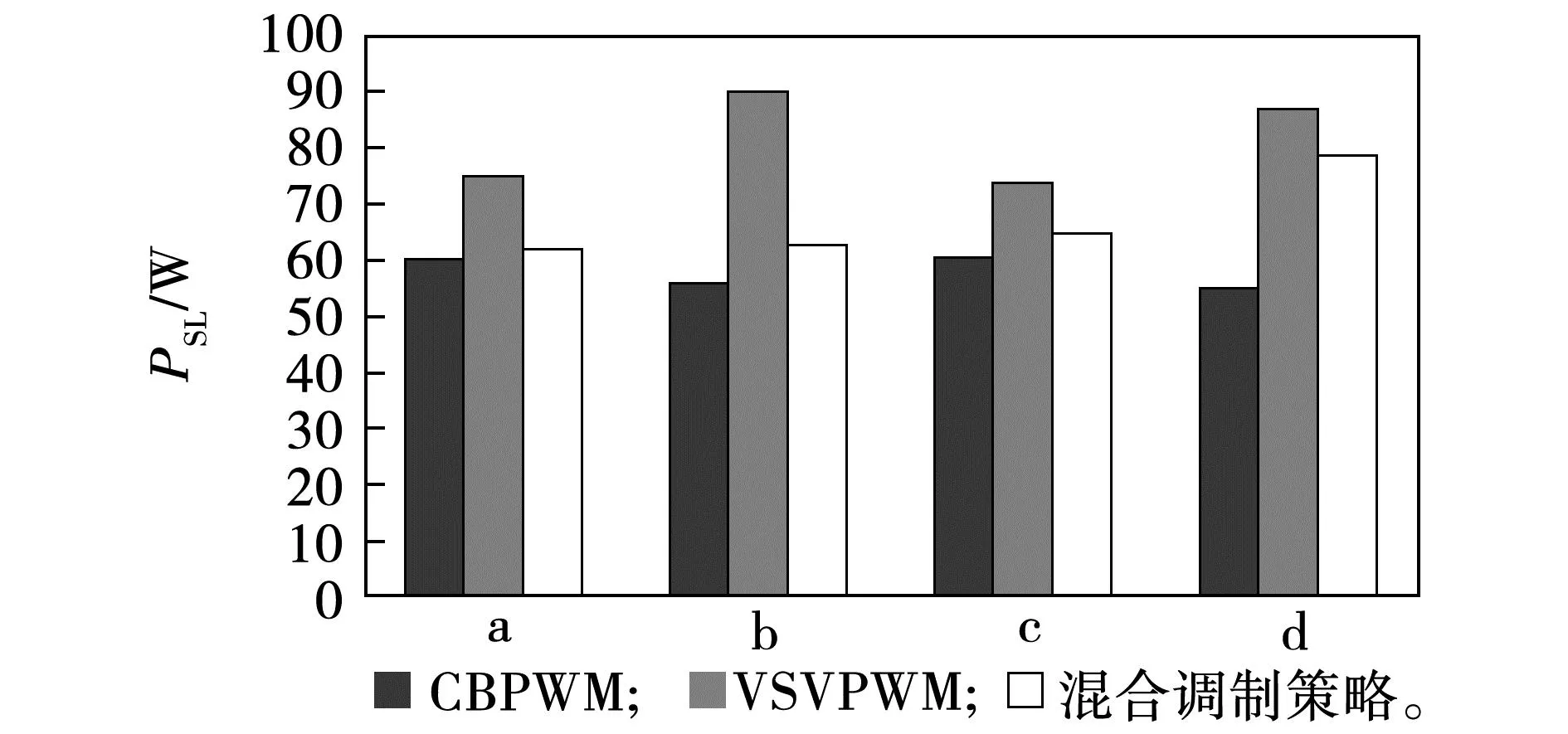
图13 不同调制策略下的开关损耗

另外,表3还给出了不同调制策略下相电流ia的THD。可以看出,CBPWM在中点电压存在三倍频波动时输出电流质量最差,在中点电压可以平衡时输出电流质量最好。VSVPWM和本文所提的混合调制策略能完全平衡中点电压,故其谐波含量相对较低。

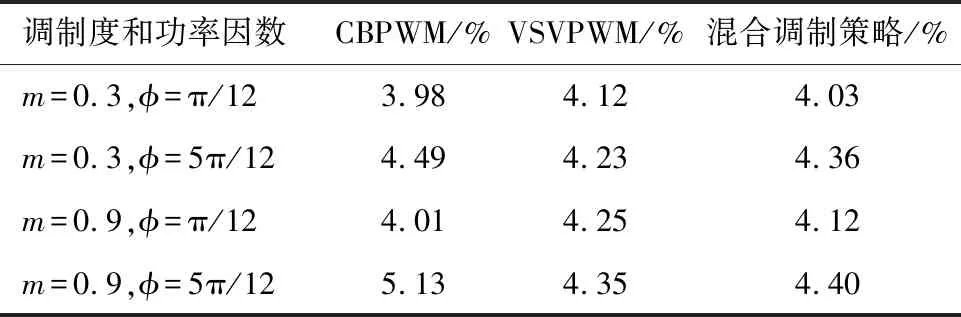
表3 不同调制策略下ia的THD

5.2 动态实验

图14～图16给出了动态实验结果,包括NPV恢复、负载突变和调制度突变。

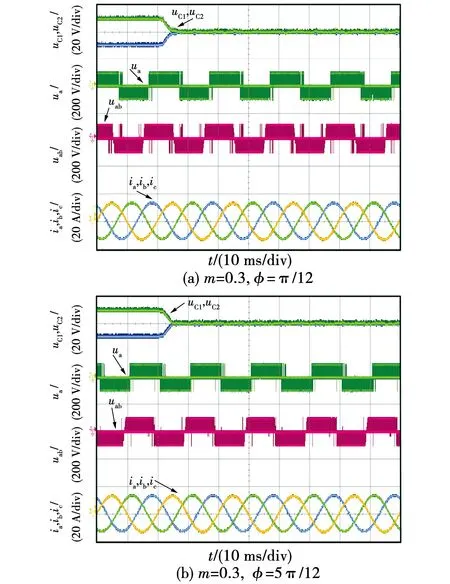
图14 混合调制策略下的NPV恢复过程

NPV恢复实验中使NPV在初始时存在20 V的偏移,使用不同调制方法使得NPV恢复到平衡状态。图14给出了采用混合调制策略时的NPV恢复过程。可以看出,混合调制策略能使NPV从不平衡状态迅速恢复到平衡状态。

图15给出了在m=0.9和φ=5π/12时,CBPWM和VSVPWM的NPV恢复过程。可以看出,虽然CBPWM最终消除了在NPV上的直流偏移,但存在着较大的交流纹波。VSVPWM具有良好的NPV恢复能力,NPV最终实现平衡。

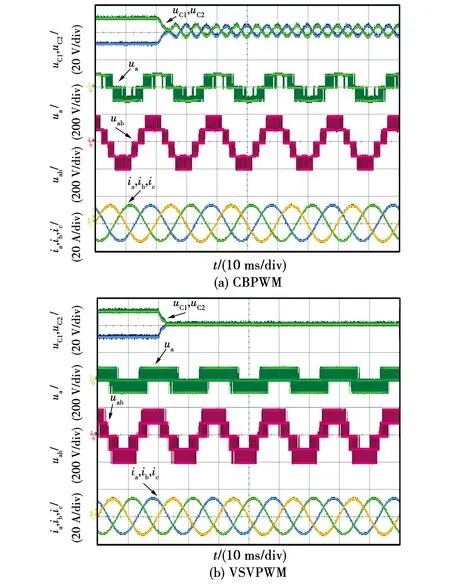
图15 当m=0.9,φ=5π/12时,CBPWM和VSVPWM的NPV恢复过程

图16给出了在混合调制策略下调制度突然变化及负载突然变化的实验结果。负载突变实验使用负载3与负载5。容易看出,在动态过程中,NPV均被很好的控制。这说明混合调制策略在动态过程中对NPV具有很强的控制能力。

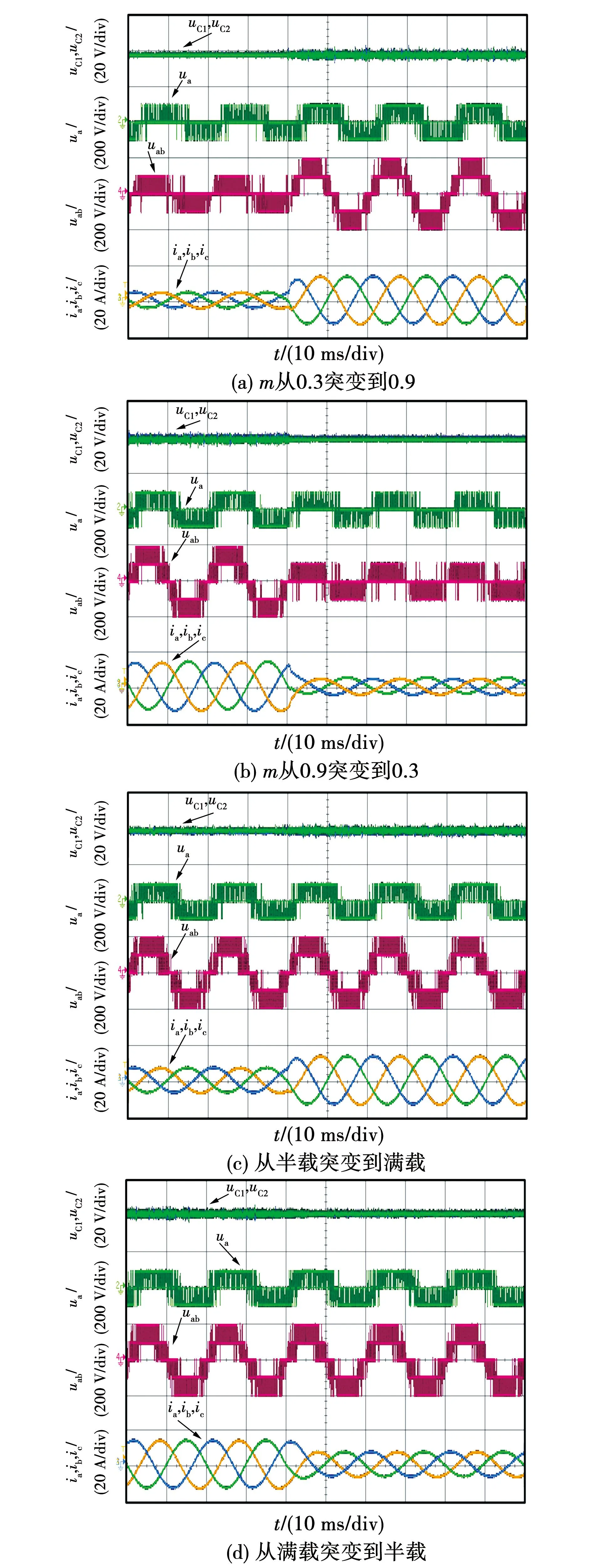
图16 混合调制策略下的动态过程

6 结 论

本文基于一种简单的调制波分解算法,对双调制波进行多种约束,以达到不同的调制目标。为了在全调制度、全功率因数范围内实现NPV平衡,本文提出了一种混合调制策略,实现了在NPV平衡的前提下开关损耗有所降低。与单纯采用某一约束相比,混合调制策略在NPV平衡方面和开关损耗方面具有一定的优势。理论分析和实验结果表明本文所提出的混合调制策略对NPV具有VSVPWM同样地控制效果,但开关损耗有所降低。