巧用函数思想妙解平面几何问题
黄永慧


摘要:函数思想是用函数的概念和性质去分析问题、解决问题的思维策略,它是初中数学的重要思想之一.在解答几何问题时,常常会遇到根据已知条件很难直接通过演绎推理求解或证明的情况,但如果能建立适当的平面直角坐标系,利用数形结合思想,结合函数解析式来解决,往往能出奇制胜,事半功倍.本文中就利用一次函数、三角函数及二次函数来妙解平面几何问题展开论述.
关键词:函数思想;妙解;平面几何问题;函数解析式;最值;动态问题
函数思想(Theory and thought of function)是解决“数学型”问题中的一种思维策略.自人们运用函数以来,经过长期的研究和摸索,科学界普遍有了一种意识,那就是函数思想,在运用这种思维策略去解决问题时,科学家们发现它们都有着共同的属性,那就是定量和变量之间的联系.
回顾数学发展的历史,早在几百年之前法国著名的数学家笛卡儿就曾提出过所谓的“万能方法”,这种方法就是把函数思想应用到几何中去,把几何问题转化为代数问题,再把代数问题归结为函数问题来解决.
解决此类问题的过程中,要善于挖掘题目中的隐含条件,构造出函数解析式和妙用函数的性质,是应用函数思想的关键.对所给问题的观察、分析与判断比较深入和充分时,会产生由此及彼的联系,构造出函数原型.另外,方程问题、不等式问题和某些代数问题也可以转化为与其有关的函数问题,即用函数思想解答非函数问题.
1 巧建平面直角坐标系利用函数妙解线段问题
在教学过程中发现,凡是可以运用函数解析法来解决的一些问题,它们的条件大都有鲜明的特征,即具备建立平面直角坐标系的条件.如在通常情况下,可以根据相对应的条件,选取合适的点为坐标原点,互相垂直的线段所在的直线为坐标轴建立平面直角坐标系来解答问题,会起到事半功倍的效果[1].
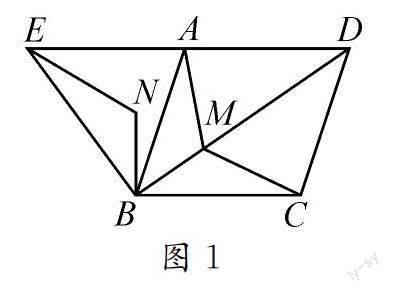
例1 如图1,四边形ABCD是菱形,且∠ABC=60°,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN,AM,CM.
(1)求证:△EBN≌△ABM.
(2)当点M在何处时,AM+BM+CM的值最小?请说明理由.
(3)在(2)的条件下,若菱形ABCD的边长为2,求BM的长度.
分析:(1)显然,根据△ABE是等边三角形和菱形ABCD的性质可证明△EBN≌△ABM.
(2)连接CE,当点M位于BD与CE的交点处时,AM+BM+CM的值最小,求出EC的值即可.
(3)根据题意可以发现BN⊥BC,M又是BD和EC的交点,故可以考虑根据一次函数图象的交点来解决点M的坐标问题,从而很容易的得到BM的长度.
根据题意建立以B为原点,以BC所在直线为x轴,以BN所在直线为y轴的平面直角坐标系,再结合菱形的性质可求出直线BD和直线CE的解析式,求出交点坐标,进而求解.
2 巧用一次函数解答动态三角形面积问题
动态面积类问题一直是学生害怕的难点问题,由于动点变化引起其他图形变化,因此在图形变化过程中很难确定具体的数量关系.这种情况下可以考虑采用函数关系来分析,即用含自变量的代数式表示因变量,根据获得的解析式进行求解会让问题变得简单容易[2].
例2 如图2,在△ABC中,AB=1,CD⊥AB于点D,E是线段CD上的动点,点F在直线AB的下方,∠ACB=∠FEB=90°,∠A=∠EFB=30°,试探求CE的长与△BDF的面积关系.
分析:由于点E是线段CD上的一个动点,因此CE的长度是一个变量,我们可以考虑它是否和△BDF的面积存在一定的函数关系.
3 巧用三角函数解答直角三角形问题
三角函数知识不仅仅可以直接用来解直角三角形,在几何问题中也可以进行综合应用,有些问题利用三角函数来解答能使问题更加明朗.如,利用三角函数的定义把握三角形边与角之间的关系,利用等角的关系可以将不同三角形的边之间的关系联系在一起,进一步优化解题思路,让平面几何问题的解答过程变得更加简捷、巧妙.
例3 如图4,Rt△ABC中有正方形DEFG,点D,G分别在AB,AC上,点E,F在斜边BC上,求证:EF2=BE·FC.
证明:因为∠A=90°,且∠CGF+∠C=∠B+∠C,所以∠CGF=∠B.在Rt△BDE中,tan B=DEBE;在Rt△CFG中,tan ∠CGF=CFFG.又根據已知条件可得DE=FG=EF,故EF2=BE·FC.
4 巧用二次函数解答四边形最值问题
二次函数最重要的作用之一就是利用函数解析式求解最值问题,因此在最值求解过程中,可以利用所给条件,列出二次函数的解析式,借助解析式分析最大值或最小值,也可以借助二次函数图象判断最值问题.
例5 某市进行河滩治理,优化美化人居生态环境.如图5所示,在河畔的一处滩地上规划一个五边形河畔公园ABCDE.按设计要求,要在五边形河畔公园ABCDE内挖一个四边形人工湖OPMN,使点O,P,M,N分别在边BC,CD,AE,AB上,且满足BO=2AN=2CP,AM=OC.已知五边形ABCDE中,∠A=∠B=∠C=90°,AB=800 m,BC=1 200 m,CD=600 m,AE=900 m.为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖OPMN?若存在,求四边形OPMN面积的最小值及这时点N到点A的距离;若不存在,请说明理由.
解析:根据图形特点,将图形补齐,如图6,分别延长AE与CD,交于点K,则四边形ABCK是矩形.设AN=x,则PC=x,BO=2x,BN=800-x,AM=OC=1 200-2x,MK=2x,PK=800-x,进而得出S四边形OPMN=4(x-350)2+470 000,故当点N到点A的距离为350 m时,四边形OPMN面积的最小值为470 000 m2.
当然,运用二次函数可以解决很多贴近生活实际的几何图形问题,取得最值的情况需要具体分析.一是在二次函数图象的顶点处取最值;二是要对多个函数分别求得最值后再通过比较获取最值;三是在不包括二次函数对称轴的一侧取得最值;四是在对称轴附近的整点处获取最值.特别是在解决具体实际应用题时,要注意根据题意灵活把握函数的有关性质,并与函数图象结合起来进行求解.
函数思想在应用过程中具有广泛性、多样性和灵活性,在教学中要重视函数思想的渗透,引导学生充分挖掘平面几何问题中的函数思想,能够巧用函数定义、性质、图象来分析问题,转化问题,解答问题,从而不断提升思维品质和数学综合素养.
参考文献:
[1]薛朝晖.平面直角坐标系中数形结合思想之巧用[J].初中生世界,2015(6):22-23.
[2]武芳.谈谈函数思想在解题中的应用[J].语数外学习(高中版下旬),2022(3):56.

