弯曲输流管路振动特性分析

侯舵，杨翊仁

（西南交通大学力学与航空航天学院，成都 611756）

引言

用于输送流体的管路系统在海洋工程、生物工程、化工机械、航空航天及核工业等工程领域中发挥着非常重要的作用。管路系统的振动问题有着重要的工程意义，它的研究成果可直接应用于上述工程领域[1-2]。众多国内外学者也对输流管路系统的流固耦合振动特性进行了研究。Olson等[3]对直管与管内流体耦合振动的有限元方法进行了综述，着重阐明了采用梁单元计算管路流固耦合问题的基本思路。Riedelmeier等[4]分析了水锤冲击过程中流固耦合作用对管路的影响。尤其在弯曲度较大的管道中，流固耦合的研究意义重大。俞树荣等[5]以流固耦合理论为基础，进行了管路双向流固耦合受力分析、单双向流固耦合对比分析和模态分析。权凌霄等[6]针对航空弯曲管路，建立了流固耦合模型，发现增加弯曲半径会导致其固有频率降低。桑勇等[7]对液压管路系统流固耦合振动特性进行分析，研究了管材参数对管路系统固有频率的影响。Wang等[8]从理论和实验方面研究了左端固支，右端简支的水平段塞流输流管的响应问题，发现液塞区速度影响着其离心力和科氏力，进而对液塞区出管时管道的响应有很大影响。谌冉曦等[9]运用ANSYS Workbench 平台建立了不同曲率半径的管路模型，分析了弯曲半径对流体压力和内部流速分布的影响，获得了弯曲半径和入口压强对固有频率和总变形之间的关系。李玺[10]基于泊松流固耦合原理，建立了动态流体模型和管道运动模型，对流固耦合进行受力分析和模态分析，对比了有无流固耦合存在时，输流管道振动模态的变化，并研究了压强、壁厚和入口速度对管道固有频率和振型的影响。韩天宇[11]对变截面直管及三通管在流固耦合作用下的振动特性进行了计算分析。吴明明等[12]对气液两相段塞流管道的稳定性进行了分析，运用数值方法求解了伽辽金方法离散后的管道振动方程。随岁寒等[13]根据虚功原理建立了输流管道系统的控制方程，研究了细长输流圆管在弹簧约束条件下的动力学特性和管道固有频率与流体粘性及弹簧刚度之间的关系。

但以上研究大多是针对某一平面内的弯管或者直管，针对非平面Z 形空间弯曲管路振动特性的研究相对较少，而管路系统大多是以空间弯曲的形态应用于诸多工程领域。基于此，本研究利用ANSYS Workbench 平台对一段非平面Z 形空间弯曲管路在流固耦合作用下的模态进行了对比分析，同时考虑了弯曲半径、管内介质、管材弹性模量等不同因素对振动特性的影响。研究结果可以为此类弯曲管路的振动控制和设计安装提供一定依据和参考。

1 流固耦合模态分析基本理论

模态分析可用于确定结构的固有频率和振型，进而识别系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。通常模态分析在空气中进行，空气密度小，对模态分析结果影响较小，在计算时可以忽略空气的作用，称为干模态分析。但对于受密度较大流体（如水、燃油等）作用的结构，由于流体附加质量及刚度的影响，在进行模态分析时则需考虑液体与固体的耦合作用，称为湿模态分析。

设流体是均匀、无黏、无漩的理想流体，由流体运动方程和连续条件可知流体波动方程为：

式中，∇2表示拉普拉斯算子，p为流体压力，C为流体介质中的声速。

采用加权余量的Galerkin 方法进行离散化，流场内任一点的压力分布p(x,y,z,t) 可表示为：

式中，mf为流体单元的结点数，Ni(x,y,z)为流体单元形状函数，Nf为流体形状函数矢量，p为流体单元的压力函数矢量。此时式（1）满足：

式中，R为余量。用Galerkin 法对全流体域进行积分：

式中，Vf为全流体域体积，对式（4）的第一项用分部积分法可以化为：

式中，S为流体域的边界面积，nf为流体边界面的外法线单位向量。将式（2）和流体流固交界处、自由表面、固定边界、无限远边界处的边界条件代入式（5）并经离散化后，流体运动方程可表示为：

式中，Mf、Cf、Kf分别为流体质量矩阵、阻尼矩阵和刚度矩阵，Q=为流固耦合矩阵，ρf为流体质量密度，Ns为固体形状函数矢量，ns为流固交界面上固体边界面的外法线单位向量，S0为流固交界面面积，u为固体位移矢量。在考虑流体对固体作用力的情况下，用有限元法可得固体结构的运动方程为：

式中，Ms、Cs、Ks分别为固体结构的质量矩阵、阻尼矩阵和刚度矩阵，Fs为固体外激励载荷矢量。若在实际分析时不考虑流固系统的阻尼效应及外界载荷矢量，可以得到系统的无阻尼自由振动有限元方程为：

对不可压缩流体，同时忽略自由液面的影响，此时Mf=0，式（8）可写为：

2 弯曲管路模型建立与湿模态分析

2.1 空间弯曲管路几何模型的建立

工程中应用的管路系统多按弯曲管路或空间曲管形式进行布置。利用式（9）的特征方程，基于ANSYS Workbench 平台，在复杂的管路系统中选择一段非平面Z 形空间弯曲管路进行研究和计算，其几何示意图如图1所示。

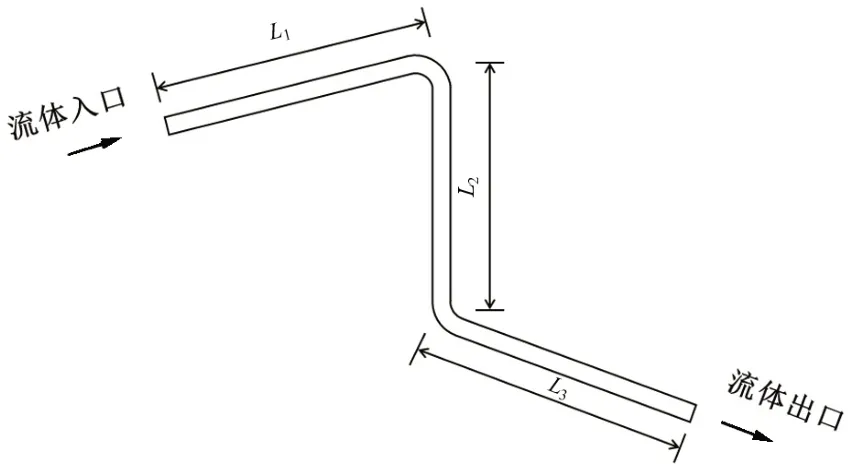
图1 非平面Z形空间弯曲管路几何示意图

空间弯曲管路管道材料为DN50 的标准无缝钢，其内径为53 mm，壁厚为3.5 mm，弯曲中心线半径R=100 mm，入口段L1=800 mm，中间段L2=800 mm，出口段L3=800 mm，管路具体参数见表1。

表1 管路系统参数

2.2 弯曲管路湿模态分析

考虑流固耦合作用时的模态分析即湿模态分析。为了探究流固耦合作用对此弯曲管路模型结构模态的影响，利用ANSYS Workbench 平台中Modal 模块和Modal Acoustics 模块分别计算无流体作用的弯曲管路和考虑流体作用的弯曲管路结构模态。在Geometry 模块中建立有限元模型，利用Fill 功能创建流体模型，将管道与内部流体合并为一个Part，确保在划分网格时流固交界面上共节点[14]。管道采用Solid186 三维实体单元，内部流体采用Fluid220 三维声学流体单元，选择扫略方式对管道和内部流体进行网格划分，网格划分完成后如图2 所示。其中外部管道共有114 380 个节点，26 670 个单元，内部流体共有56 050 个节点，13 070个单元。

图2 管道及内部流体模型网格划分

计算时采用直接耦合方式，弯曲管路两端环形面上施加位移约束，其X、Y、Z方向位移分量均设置为0[15]。计算完成后得到干、湿模态前六阶固有频率对比见表2。

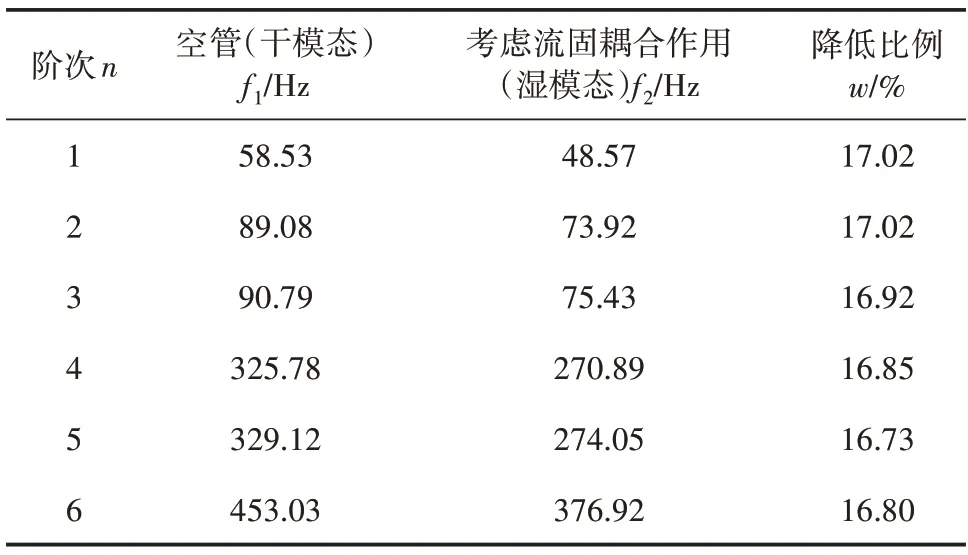
表2 空间弯曲管路前六阶固有频率

由表2 可知，流固耦合作用使弯曲管路前六阶固有频率均降低约17%。这充分说明对于受流体作用的结构，特别是密度较大的流体（如本例中的水），在进行模态分析时就需要考虑流体与固体的耦合作用，这种流固耦合作用会降低管路结构的固有频率，故计算湿模态是非常必要的，其影响不可忽略。

湿模态计算下的结构前六阶振型如图3 所示，从图3 中可以看出，弯曲管路的前六阶模态振型均为横向弯曲振动形态，故弯曲管路的变形以横向弯曲振动为主。对比文献[16]中干模态下振型图与图3 中湿模态下振型图可知，考虑内部流体和管道耦合作用的模态振型与不考虑流体作用的空管模态振型基本一致，这表明管道内部流体与管路的耦合作用对管道的模态振型没有影响。

图3 流固耦合作用下的管道前六阶模态振型

3 不同因素下振动特性分析

为研究不同因素下空间弯曲管路的振动特性，采用湿模态分析方法，选取弯曲半径、管内介质、管材弹性模量等分别作为变量进行模态对比分析，探究其对固有频率的影响。图1中空间弯曲管路共有两段弯曲段和3 段直管组成，为研究弯曲段中心线半径对管路固有频率的影响，取两段弯曲段的弯曲半径均分别为100、120、140、160 mm，其他参数不变，得到弯曲管路前六阶固有频率如图4 所示。从图4 中可见，弯曲管路弯曲段半径增加20 mm，前六阶固有频率分别相应增加1.0%、3.0%、2.6%、0.2%、0.3%、1.9%，这是因为弯曲半径的增大会使管路显得更“直”，但其对固有频率的影响并不明显。

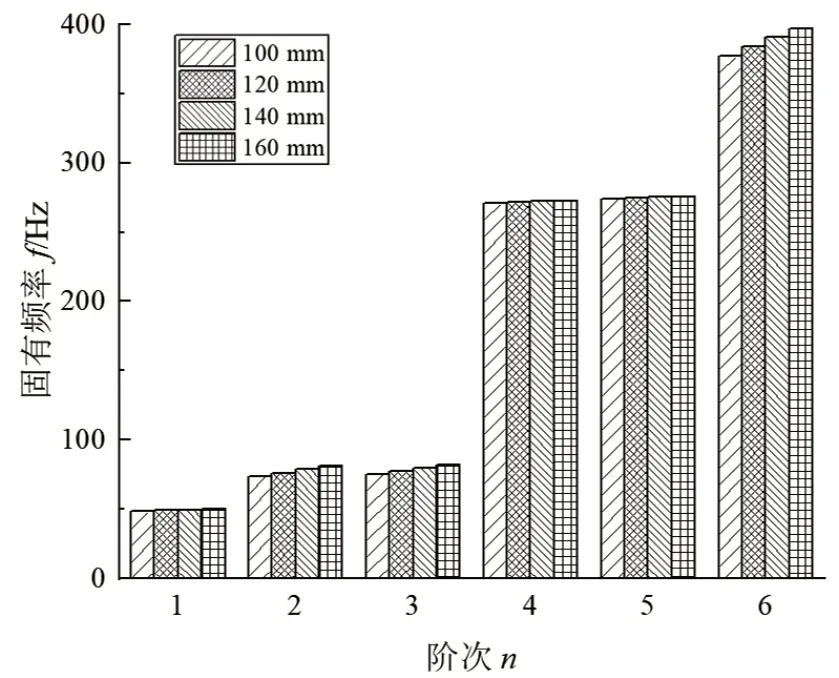
图4 弯曲管路不同弯曲半径下前六阶固有频率对比

在初始仿真条件不变的基础上，分别将管内流体介质设置为空气、柴油、原油（流体介质参数见表3），计算出弯曲管路内输送不同介质时前六阶固有频率如图5所示。由图5可见，流体介质由空气变为柴油，前六阶固有频率均减小约13.0%，流体介质由柴油变为原油，前六阶固有频率均减小约3.7%。表明流体介质密度越大，其附加质量也越大，增强了其与管道的流固耦合作用，使管路的“柔”性越强。图5中空气与管路耦合作用下的前六阶固有频率与表2中空管的固有频率非常接近，这表明空气与管路之间的耦合作用可以忽略，即在空气中进行的模态分析可以忽略空气对固体结构固有频率的影响。

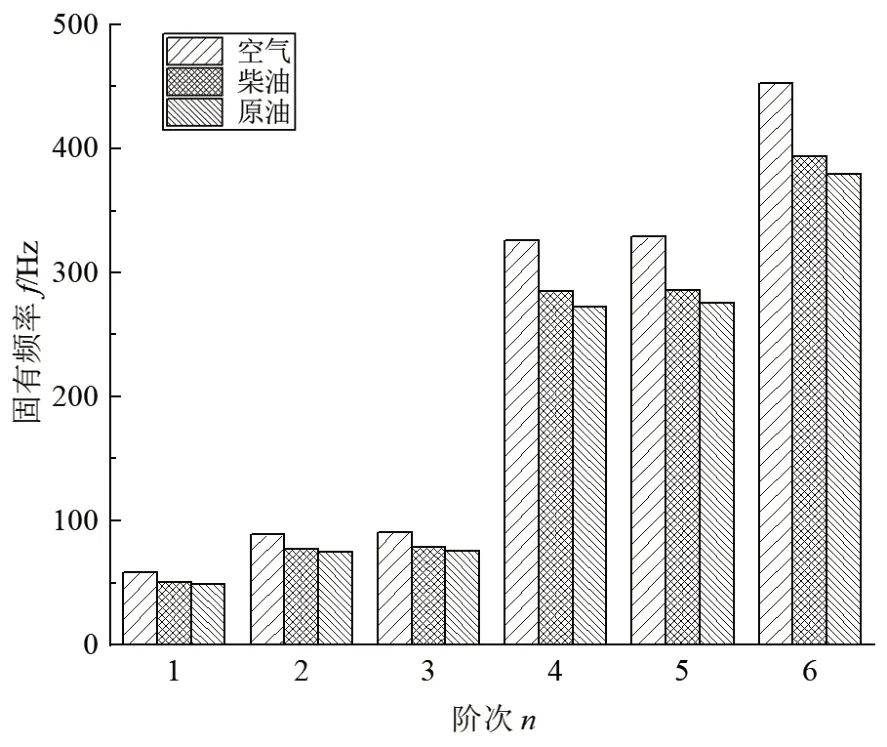
图5 管内不同介质下前六阶固有频率对比

由材料力学知识可知，材料在弹性变形阶段，其纵向应力和纵向应变符合胡克定律，其比例系数称为弹性模量，是描述固体材料抵抗形变能力的物理量。将管路弹性模量作为变量，分别取为190、200、210、220 GPa，计算出各弹性模量下前六阶固有频率如图6所示，图中可见弹性模量每增加10 GPa，前六阶固有频率均增加约2.5%。因弹性模量的大小反映了材料的刚性，故在选取输流管路管材时应考虑材料刚度的影响，选择刚度或弹性模量较大的管材，可以有效提高管路的固有频率。

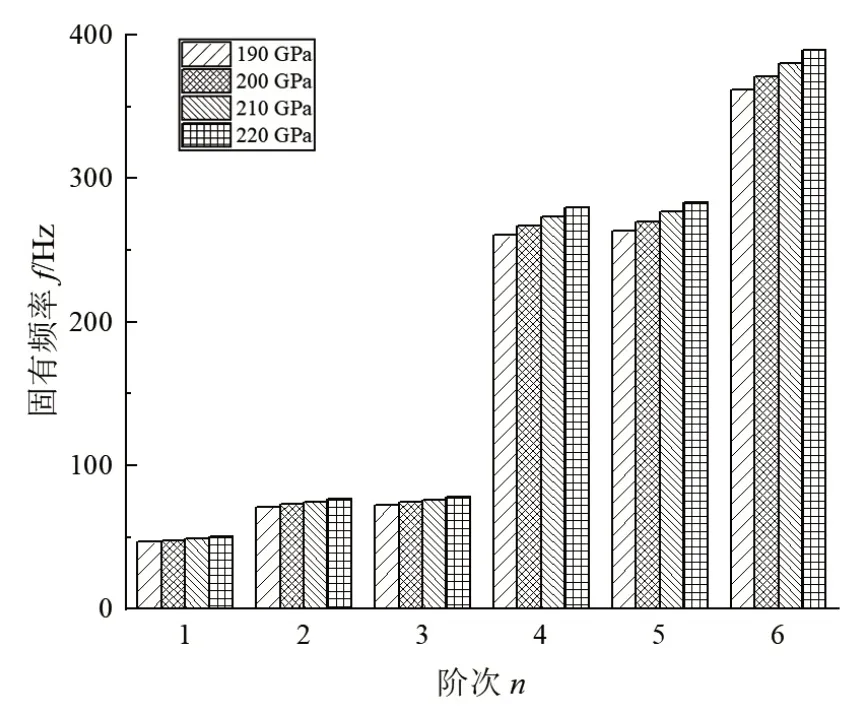
图6 管道不同弹性模量下前六阶固有频率对比

4 结论

以一段非平面Z 形空间弯曲管路为研究对象，建立其有限元模型，利用ANSYS Workbench 平台进行了流固耦合模态分析，探究了管路弯曲半径、管内输送介质、管材弹性模量对空间弯曲管路模态的影响，并得出以下结论：

1）管路与流体的耦合作用会降低本研究中非平面Z 形空间弯曲管路固有频率，前六阶固有频率降幅约17.0%，故在进行模态分析时，尤其管内输送介质为密度较大的流体时，需考虑流固耦合作用对结构模态的影响。

2）本研究中空间弯曲管路前六阶模态振型均属于横向弯曲振动形态，流固耦合作用对管道的模态振型影响甚微。

3）本研究中空间弯曲管路固有频率会因各因素的改变而变化，具体为管路弯曲转角半径每增加20 mm，前六阶固有频率增大1.0%～3.0%，而管内输送流体由空气变为柴油时，前六阶固有频率减小约13.0%，由柴油变为原油时，前六阶固有频率减小约3.7%，管材弹性模量每增加10 GPa，前六阶固有频率增大约2.5%，可见管内输送流体介质的密度对固有频率的影响显著。