内曲线液压马达低应力三层复合轴瓦厚度分配

李莹 王博众 何双 刘彦东 张晋

（1.燕山大学 机械工程学院，河北 秦皇岛 066004；2.燕山大学 河北省重型机械流体动力传输与控制实验室，河北 秦皇岛 066004）

液压传动广泛应用于工业生产领域［1］，其中内曲线液压马达由于具有转速低、扭矩大等特点，已广泛应用于锚绞机、盾构机、注塑机和矿山机械等领域［2-3］。由于长期在重载工况（28 MPa 以上）下运行，内曲线液压马达的寿命和可靠性面临严峻的考验。提高马达寿命和可靠性最有效的方法之一就是提高马达关键摩擦副的寿命，保证马达摩擦副长期稳定的工作。

如图1所示，内曲线液压马达关键摩擦副包括配流副、柱塞-转子副、滚柱-柱塞副、滚柱-定子副等［4］。由于滚柱-柱塞副低速时难以建立动压润滑油膜，因此当内曲线液压马达处于低速时，极易产生“窜动”，摩擦产生的大量热量还会引起滚柱、柱塞热变形，导致滚柱-柱塞“咬死”，破坏马达结构，造成内曲线液压马达失效［5］。

图1 内曲线液压马达关键摩擦副Fig.1 Key friction pair of cam lobe hydraulic motor

国内外研究人员提出了两种解决方案，以提高滚柱-柱塞副的低速润滑性能：①通过在柱塞内设计阻尼孔，将柱塞底部的高压油引入滚柱-柱塞间隙，并在柱塞与滚柱接触的内表面设计流道，为滚柱-柱塞副提供静压支撑［6］。该方案通过静压支撑保证滚柱与柱塞间充分润滑，但由于柱塞腔高压油在滚柱-柱塞间隙还会发生泄漏，因此采用该方案的内曲线液压马达容积效率会略有降低。②在滚柱-柱塞副中设置自润滑轴瓦，保证边界润滑时滚柱与柱塞间仍能维持较低的摩擦系数。该方案不会引起额外泄漏，因此容积效率不受影响，马达效率更高。国外液压马达厂商波克兰采用该方案，其MS 系列内曲线液压马达具有承载能力和效率高等特点。由于轴瓦承载能力不足，目前采用同方案的国产内曲线液压马达最大工作压力仍与波克兰马达存在一定的差距。

自润滑轴瓦所使用的自润滑材料，如PEEK（聚醚醚酮）、PTFE（聚四氟乙烯）等，相比于金属材料，虽然可以显著降低摩擦系数，但其机械强度、导热性和耐热性较差，难以承受较大载荷，发热后易产生变形。因此，通常将自润滑材料加工成钢背-铜粉-自润滑材料结构的三层复合轴瓦用于低速大扭矩液压马达滚柱-柱塞副，以提高自润滑材料的承载能力［7］。

目前，针对轴瓦自润滑层材料的摩擦学性能的研究较多［8-11］，大多集中于分析改性自润滑材料的摩擦学性能。但有关三层复合轴瓦结构参数对力学性能的影响规律的研究较少。Zhang 等［12］建立了一个计算三层复合结构热残余应力的数学模型，并分析了层厚对热残余应力的影响规律。丘佛球［13］分析了轴瓦总厚度对承载能力和疲劳强度的影响，发现随着轴瓦总厚度的增加，应力分布越均匀，但疲劳强度降低。陈凯航［14］制备了钢背/铜粉/PTFE板，利用数字图像关联技术和电子背散射衍射技术探究了三层复合板材的变形特性，并分析了三层复合轴瓦的成型性能。以上研究分析了部分影响力学性能的因素，但并未分析三层复合结构各层层厚参数对承载能力的影响，而厚度分配对轴瓦承载能力具有不可忽视的影响。目前，三层复合轴瓦各层的厚度分配只能通过试验试错，缺少理论支撑，多种规格试验样件加工周期长，测试成本高，因此探究三层复合轴瓦厚度分配方法，可以提高研发效率。同时，合理分配各层厚度可以有效地提高轴瓦承载能力，对提高内曲线液压马达承载能力至关重要。

本研究通过建立柱塞组件有限元模型，分析了三层复合结构各层厚度和轴瓦应力的映射关系，提出了一种低应力三层复合轴瓦厚度分配设计方法，并提出了一种适用于低速内曲线液压马达滚柱-柱塞副的低应力三层复合自润滑轴瓦厚度分配方案。

1 三层复合轴瓦有限元模型

1.1 三层复合轴瓦受力分析

三层复合轴瓦安装于内曲线液压马达滚柱-柱塞副中，与滚柱、柱塞共同组成柱塞组件。如图2所示，内曲线液压马达工作时，高压油驱动柱塞组件压紧定子，使柱塞组件沿定子运动，柱塞组件受到定子的反作用力，带动缸体转动，向外输出扭矩。由于轴瓦在滚柱对轴瓦内径表面的压力和柱塞对轴瓦的支撑力作用下受力平衡，因此为计算轴瓦所受载荷，对滚柱进行受力分析。如图2所示，滚柱所受外力包括定子的反作用力N、轴瓦支撑力Fzw、轴瓦与滚柱间的摩擦力Ff、离心力Fω、径向加速度引起的惯性力Fr和科氏加速度引起的惯性力Fk。

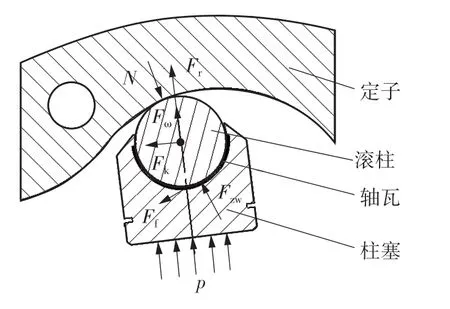
图2 内曲线液压马达轴瓦的受力模型Fig.2 Force model of bearings of an inner curve motor

离心力、径向加速度引起的惯性力和科氏加速度引起的惯性力计算公式如下：

式中，m为柱塞组件质量，ω为马达转子的角速度，ρ为柱塞组件质心到马达转子轴线的距离，a为柱塞组件相对加速度，v为柱塞组件相对线速度。

内曲线液压马达柱塞组件质量为1 kg，假定内曲线为余弦加速度曲线时，计算得到3种惯性力数值相加，最大值约为3.5 N。当柱塞腔压力p超过2 MPa 时，柱塞组件所受液压力约为5 284 N，惯性力对液压力的影响不足0.1%。因此，在分析轴瓦所受载荷时，3 种惯性力可以忽略［15］。定子的反作用力与柱塞腔压力的关系可近似为

式中，d为滚柱直径，α为压力角（即定子的反作用力与柱塞轴线的夹角）。

轴瓦实际工作过程中除了受到滚柱的压力外，还受到摩擦力的共同作用。由于摩擦力只存在于接触面切向方向，不会对正应力产生贡献，因此在分析轴瓦承载能力时可以忽略滚柱与轴瓦间的摩擦力，只考虑滚柱对轴瓦表面的正压力。轴瓦表面所受载荷近似为定子的反作用力N。将轴瓦应用于一款最大工作压力为31.5 MPa 的内曲线液压马达，仿真中为了确保轴瓦内表面所受压力满足实际工作时的最大压力，并具有一定的超载余量，设置柱塞底部仿真压力为35 MPa。

1.2 三层复合轴瓦有限元模型的建立及验证

根据内曲线液压马达滚柱-柱塞副真实结构尺寸建立柱塞组件几何模型，其中滚柱外径为40 mm，由于滚柱与轴瓦间需要存在一定的热变形余量和润滑油膜，轴瓦内径为40.12 mm，三层复合轴瓦总厚度为1.5 mm，轴瓦外径为43.12 mm，柱塞凹槽内径与轴瓦外径相同。轴瓦宽度与柱塞凹槽宽度一致，均为40 mm。

利用Ansys Workbench 建立静力学仿真模型。首先设置模型中各部分材料属性。根据内曲线液压马达实际使用材料（滚柱材料为GCr15SiMn，自润滑层材料为PEEK，铜粉层材料为CuSn8P，钢背层材料为Q195），得到对应材料的属性如表1所示。

表1 材料属性Table1 Material properties

为模拟轴瓦实际受力状况，仿真模型包括定子、滚柱、轴瓦、柱塞。其中滚柱与定子、滚柱与轴瓦之间为线接触，且可以发生滑移，因此滚柱-定子、滚柱-自润滑层接触形式设置为无分离。轴瓦分为自润滑层、铜粉层、钢背层。轴瓦自润滑层、铜粉层和钢背层之间通过烧结、轧制连接，即自润滑层-铜粉层、铜粉层-钢背层均不存在位移，接触类型设置为绑定，轴瓦固定安装在柱塞凹槽内，在运行过程中不会发生相对位移，因此设置为绑定。

为了确保轴瓦承载能力满足内曲线液压马达的极端工况，仿真中需要将边界条件设置为轴瓦内表面压力最大瞬间工作参数。根据内曲线液压马达柱塞组件工作原理，柱塞底部受到柱塞腔高压油压力的作用，根据1.1节的计算结果，设置柱塞底面压力为35 MPa。在实际液压马达中，柱塞外圆柱面受到转子柱塞腔壁面的约束，由于转子对轴瓦承载能力没有直接影响，仿真模型通过在柱塞外圆柱面设置位移约束模拟转子对柱塞的约束作用。为防止滚柱受载时沿滚柱轴向移动，在滚柱两端面设置位移约束。定子不与滚柱接触的面设置为固定约束，与内曲线液压马达中定子的状态一致。边界条件设置如图3所示。

图3 边界条件设置Fig.3 Boundary condition settings

三层复合轴瓦的内径、外径和轴向宽度远大于轴瓦厚度，且结构较为简单，因此采用多区域法划分网格，每层材料均划分为三层网格，共划分为9层网格，网格划分结果如图4所示。

图4 三层复合轴瓦的网格划分结果Fig.4 Meshing results of three-layer bearing

为保证仿真结果的准确性，避免因网格尺寸影响仿真计算结果，文中进行了网格无关性分析。由于文中主要探讨轴瓦各层厚度对应力大小及分布的影响，重点验证轴瓦各层间接触面和轴瓦-滚柱接触面的网格尺寸与仿真结果的无关性。划分不同尺寸的接触面网格，对比不同网格尺寸下得到的PEEK 层最大应力，计算结果如表2 所示。由表中可知，接触面网格尺寸为1.1 mm 时得到的最大应力与网格尺寸为0.9 mm 时相差不足1%，且网格数相比网格尺寸为1.3 mm时只增加8%左右，因此接触面加密网格尺寸设置为1.1 mm。

表2 网格无关性验证Table 2 Grid independence verification

定子、滚柱和柱塞的尺寸较大，网格设置为四面体网格，网格尺寸设置为2.5 mm。由于滚柱与轴瓦自润滑层接触，柱塞凹槽内表面与轴瓦钢背层接触，两接触面网格尺寸相差过大会影响计算精度，因此对滚柱外圆柱面、柱塞凹槽内表面、定子内表面进行加密，设置面网格尺寸为1.1 mm。

1.3 静力学仿真分析理论基础

接触问题的有限元分析是基于最小势能原理：在给定外力作用下，在所有满足位移边界条件的位移场中，真实的位移场总是使总势能取极小值。

假设有限元模型中每个节点所受外力为Fi，边界面上的压力为pi，对应节点产生的位移为ui，则外力势能W为

每个节点的应力为σi，对应节点的应变为εi，则应变势能U为

总势能E=U+W，当总势能取极小值时，总势能的一阶变分为0，即

其中应变ε可以根据几何方程用位移u表示，即总势能为位移的泛函。根据式（7）可求解应力、应变。

2 有限元仿真分析

2.1 轴瓦各层厚度的分配

为分析钢背层、铜粉层、自润滑层厚度变化对轴瓦应力的影响规律，特别是弹性模量较低的自润滑层应力，需要分配各层厚度并进行静力学仿真。根据文献［14，16-17］，铜粉层厚度范围通常为0.1～0.5 mm，自润滑层为PTFE时厚度范围通常为0.01～0.15 mm。这是因为PTFE 本身的抗拉强度较小，厚度过大时在重载下会产生严重变形甚至失效。但PEEK的抗拉强度和弹性模量远高于PTFE，自润滑层为PEEK 时，厚度超过0.15 mm 也不会在重载工况下变形，且增加自润滑层厚度，可以保证自润滑层磨损后仍有较大余量，延长轴瓦的寿命，因此自润滑层为PEEK时，通常厚度范围为0.1～0.5 mm。钢背层在三层复合轴瓦中只起到支撑作用，因此其厚度根据其余两层厚度确定。各层厚度分组如表3所示。

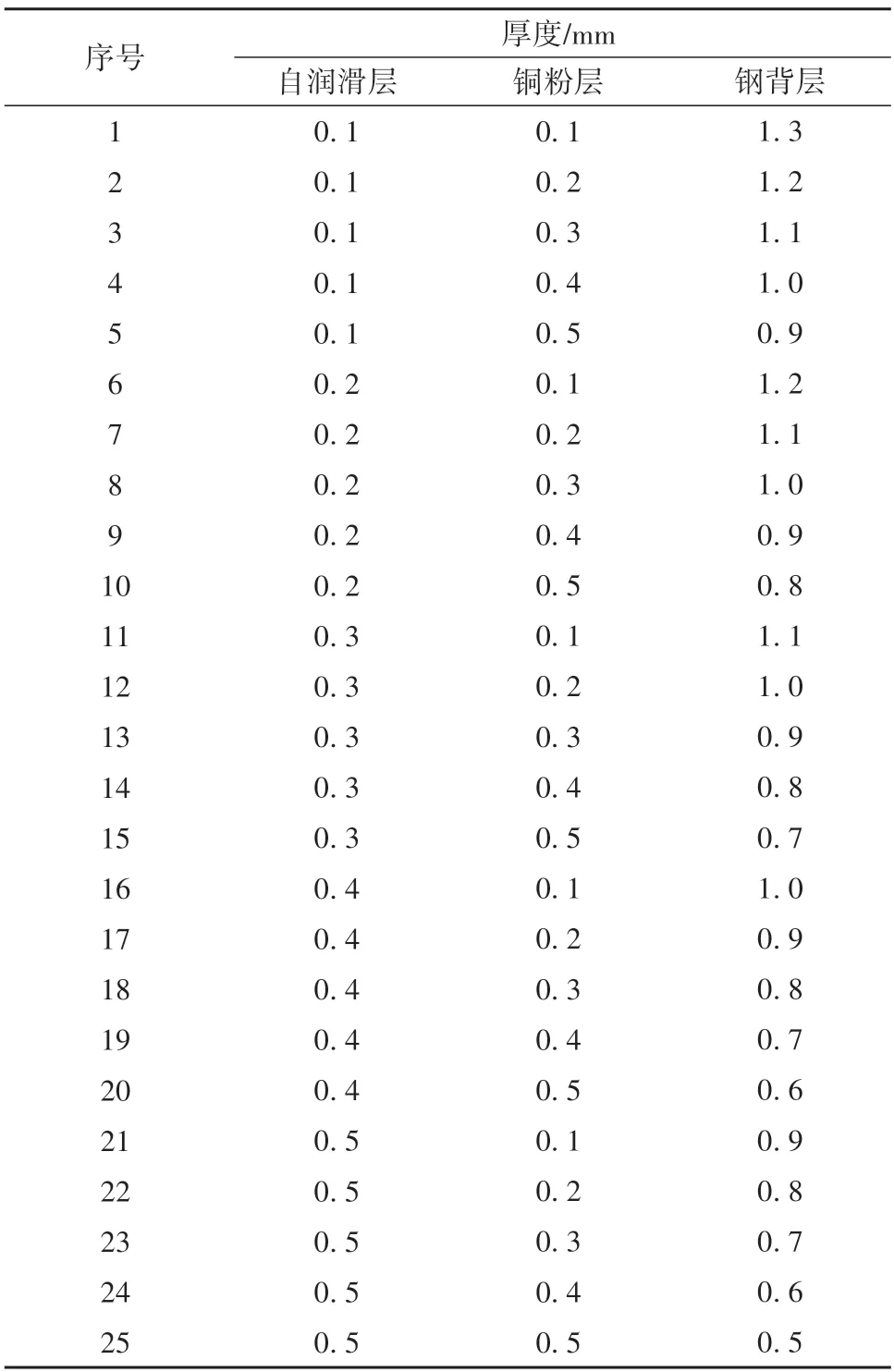
表3 三层复合轴瓦各层厚度分组Table 3 Thickness grouping of each layer of three-layer bearing

2.2 各层厚度与最大等效应力的关系分析

根据静力学仿真得到不同厚度分组下轴瓦最大等效应力和自润滑层最大等效应力，计算自润滑层厚度相同的5组仿真结果的平均值，得到轴瓦最大等效应力平均值和自润滑层最大等效应力平均值，如图5所示。

图5 最大等效应力平均值与自润滑层厚度的关系Fig.5 Relationship between the average maximum equivalent force and the self-lubricating layer thickness

随着自润滑层厚度由0.1 mm 增加至0.5 mm，三层复合轴瓦最大等效应力平均值和自润滑层最大等效应力平均值均呈现先减小后增大的规律。这是由于各层材料属性不变时，三层复合结构各层厚度的变化会导致轴瓦整体刚度矩阵的变化，进而影响各层间接触面的载荷分布，引起应力变化。根据图5可知，在自润滑层厚度为0.2 mm时，复合轴瓦应力和自润滑层应力取得最小值。

当自润滑层厚度为0.2 mm 时，复合轴瓦和自润滑层的最大等效应力随铜粉层厚度的变化关系如图6所示。复合轴瓦最大等效应力随铜粉层厚度的增加而降低，自润滑层最大等效应力基本保持不变。但实际加工三层复合轴瓦时，铜粉层使用的铜粉直径约为0.01 mm，烧结后铜粉间存在孔隙，当铜粉层厚度过大时，铜粉堆叠为多层，自润滑材料难以进入过深的孔隙，与铜粉层、钢背层的结合强度降低，自润滑层易剥落［14］。且加工三层复合轴瓦需要将三层复合板材进行卷板，当铜粉层厚度过大时，卷板过程中铜粉发生位移，三层复合轴瓦易产生凹陷等缺陷。因此，综合考虑加工工艺和力学性能，文中铜粉层厚度选为0.3 mm。

图6 自润滑层厚度为0.2 mm 时最大等效应力与铜粉层厚度的关系Fig.6 Relationship between the maximum equivalent force and the copper powder layer thickness when the selflubricating layer thickness is 0.2 mm

2.3 应力应变分布分析

根据仿真结果可知，自润滑层厚度为0.2 mm、铜粉层厚度为0.3 mm 时，复合轴瓦最大等效应力最小。在该厚度分配下，轴瓦的应力应变云图如图7所示。从图7（a）可知，轴瓦内表面即自润滑层表面的等效应力在接触区域较大，在靠近轴瓦两端面处取得最大值，铜粉层与自润滑层的应力分布状态一致，铜粉层最大应力点即是轴瓦最大应力点，最大等效应力为93.914 MPa。

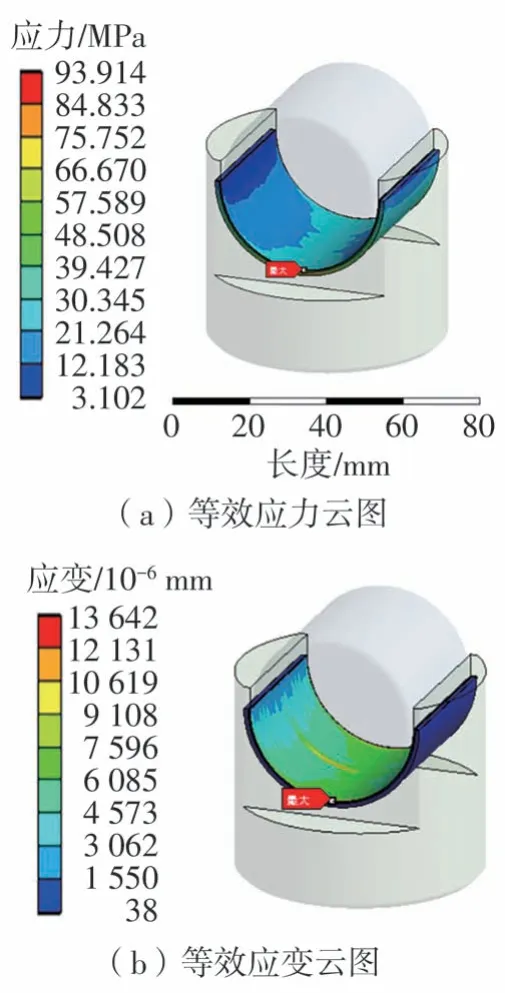
图7 三层轴瓦的等效应力、应变云图Fig.7 Equivalent stress and strain contours of three-layer bearing

从图7（b）中可知，轴瓦最大等效应变发生在自润滑层沿轴向两端面处，与应力集中区域一致，最大应变量为0.014 mm。由于柱塞组件的运动特性主要受滚柱运动特性的影响，最大应变量远小于滚柱直径40 mm，即该应变量对柱塞组件运动特性的影响较小。

3 试验分析

3.1 试验装置

为验证自润滑层厚度为0.2 mm、铜粉层厚度为0.3 mm 的三层复合轴瓦满足内曲线液压马达的实际使用需求，文中将该轴瓦安装在液压马达滚柱-柱塞副中进行承载能力装机试验，液压马达测试试验台如图8所示。该试验台为液压补偿型功率回收试验台，被测液压马达由液压泵提供高压油，根据压力计示数调整溢流阀，从而控制被测液压马达入口压力（即柱塞组件底部压力）。被测液压马达通过联轴器连接负载泵，负载泵与液压泵共同为被测液压马达供油，该试验台不仅可以精准控制试验参数和边界条件，还可以通过液压补偿回路节约试验所需能源。

图8 液压马达测试试验台Fig.8 Hydraulic motor test bench

测试使用的内曲线液压马达额定压力为25 MPa，额定转速为30 r/min，最高工作压力为31.5 MPa。该型号马达在常用工况下的最大压力不超过28 MPa，且功率一定时，马达压力越大，转速越低；当马达工作压力达到或超过28 MPa 时，转速通常小于1 r/min。

为验证三层复合轴瓦的承载能力满足内曲线液压马达的最大工作压力，且在极端使用条件下满足超负荷运行能力，测试时内曲线液压马达分别在5.1、10.0、15.0、20.0、25.0、30.0 和34.8 MPa下以30 r/min 工作1 h，最大测试压力超过最大工作压力，累计运行7 h。

同时转速固定为30 r/min，增加磨损速率和发热量，以验证极端工况下三层复合轴瓦中自润滑层厚度和热变形是否满足马达使用需求。测量记录马达入口压力、流量和输出扭矩、转速等参数，根据容积效率计算公式计算马达容积效率，以验证轴瓦性能满足要求。容积效率计算公式为

式中，Vll为空载排量，Vls为负载时排量，qll为空载入口流量，qls为负载时入口流量，nl为空载转速，ns为负载时转速。

3.2 试验结果分析

试验测得马达空载排量为6 035 mL/r，各压力下的试验数据如表4所示。

表4 马达试验数据Table 4 Experimental data of the motor

使用自润滑层厚度为0.2 mm、铜粉层厚度为0.3 mm 的三层复合轴瓦的内曲线液压马达，在不同压力等级下的容积效率始终超过《JB/T 8728—2010 低速大转矩液压马达》对内曲线径向柱塞马达容积效率的要求。

测试后拆解液压马达，观察试验后三层轴瓦的形变情况及自润滑层表面磨损情况（如图9（a）所示），发现：试验后轴瓦的表面只有轻微磨痕，未产生严重磨损，说明马达耐磨性满足需求；自润滑层表面未发生压溃或明显变形，说明承载能力满足要求。

图9 马达测试后轴瓦状态和轴瓦磨损位置Fig.9 Bearing state after motor testing and bearing wear location

根据该型号内曲线液压马达使用后反馈，长期工作在低速重载工况下的轴瓦严重磨损的位置如图9（b）所示，严重磨损区域在轴瓦内表面靠近两端面处，该位置与仿真得到的应力应变集中区域基本吻合，证明了仿真结果可靠。

4 结论

文中针对三层复合轴瓦厚度分配，通过受力分析和仿真模拟及装机试验测试的方法进行了研究，得到的主要结论如下：

（1）通过建立三层复合轴瓦的有限元仿真模型，分析不同轴瓦厚度分配方案的力学特性，可以得到合理的厚度分配方案，该方法可以有效地提高轴瓦厚度分配方案的设计速度。通过测试安装该厚度分配方案的内曲线液压马达性能，可以验证厚度分配方案的合理性。

（2）在各层材料不变时，三层复合轴瓦各层厚度的变化会影响轴瓦刚度矩阵，进而影响层间载荷分布，因此相同载荷下轴瓦内部应力分布会产生较大的变化。轴瓦及自润滑层的最大等效应力值随自润滑层厚度的增加先下降后上升，考虑加工工艺等因素，当自润滑层厚度为0.2 mm、铜粉层厚度为0.3 mm 时，轴瓦及自润滑层的最大等效应力值最小。

（3）根据仿真结果，轴瓦自润滑层等效应力在接触区域较大，在端面处取得最大值。轴瓦等效应力较大区域与自润滑层应力集中区域基本重合。实际马达长期使用后严重磨损位置与最大等效应力位置基本吻合。

（4）在35 MPa 工作压力下，采用自润滑层厚度为0.2 mm、铜粉层厚度为0.3 mm、钢背层厚度为1.0 mm 的三层复合轴瓦的内曲线液压马达，其马达容积效率与内曲线液压马达厂商波克兰同规格产品样本参数基本一致。