基于有限元法的导电滑环刷丝成型特性分析

李俊烨 田龚强 王新鹏 李军 石广丰 袁泽彬

（长春理工大学 机电工程学院，吉林 长春 130022）

导电滑环（CSR）用于传递卫星与电池板间的电信号和控制信号，其工作性能影响卫星的整体能源安全与在轨寿命［1-2］。刷丝和环片为CSR 的关键部分，刷丝固定在电刷板上，初始状态会以一定的角度压接在环片上。工作时，刷丝与环片相互接触并导通电流，其间经常会出现电流传输不稳定的问题，因此，检测刷丝成型角度的重要性不容忽视，因为它不仅会影响结果的质量和可靠性，更会影响CSR 的使用寿命［3］。成型就是迫使刷丝发生弹塑性变形，从而形成一定的角度。目前，先进成型设备售价高、维护不便，故成本过高。因此，对于这种具有一定长度的线材，在生产批量不大且无需连续加工的情况下，需要寻找一种既简单又可靠的方式来控制好刷丝的倾斜角度，并提高成型质量，这将有利于提高CSR 的信号传输质量以及减少磨损量，对CSR刷丝成型与回弹的研究具有重要的现实意义。

许多学者对CSR的材料、性能、寿命等方面展开了深入研究。韩天棋等［4］对一种合金CSR 内部缺陷展开了研究；Poljanec 等［5］分析了滑动速度、正常负载和电流对滑动电触点的性能和行为的影响；刘兴富等［6］进行了200 万转寿命试验研究，对刷丝以及刷丝束两类不同的结构进行了信号传输与功率传输的性能检测。还有学者运用有限元模拟的方法进行研究，并分析了回弹的预测效果［7-8］。Pinto等［9］采用了与有限元法计算建模相关的结构设计方法，研究了几何形状和加强筋数量对最大板材挠度的影响。刘永财等［10］提出的大步长静力隐式有限元方法，具有计算速度快和计算精度高的优点。刘佩等［11］提出了一种基于环境振动测试和商业软件交互访问的贝叶斯有限元模型修正方法。

还有许多学者的研究重点在于控制刷丝接触偏差、刷丝装配和摩擦热等，以提高刷丝的接触质量和使用寿命。Chen 等［12］跟踪手动刷对齐装配期间的相对刷位置偏差，发现刷子对齐装配精度可以控制在±0.02 mm以内；刘蓓蓓等［13］提出了一种刷丝装配方法，分两次进行胶封的装配工艺流程，提高了刷丝工装的效率和质量；李双喜等［14］对柔性丝刷式密封的摩擦生热、散热、隔热性能进行了研究；杨景尧等［15］分析了进出口静压比与背板结构对刷式密封摩擦传热特性的影响规律；柏大炼等［16］通过利用广义塑性铰法快速评估考虑残余应力影响下钢架结构的极限承载力。

迄今为止，对CSR刷丝角度成型特性的分析研究较少。因此，文中通过有限元方法模拟刷丝角度成型的过程，探究成型的作用方式和效果，分析了刷丝应力和应变的影响因素，并提出了一种基于有限元针对刷丝角度回弹过程的测量方法，以揭示刷丝回弹现象，用既简单又实用的方式来提高刷丝角度成型的准确性。

1 有限元理论分析

1.1 显式动力学算法

在有限元计算中，显式动力学分析过程是基于显式积分规则实现的，利用显式中心差积分规则对物体运动方程进行积分：

显式过程计算效率的关键是使用对角线元素质量矩阵：

式中，M是对角线集总质量矩阵，F是施加的载荷矢量，I是内力矢量。为了表示结果，状态速度被存储为平均速度的线性插值，即

中心差分算子不是自启动的，需要定义平均速度的值。速度和加速度的初始值（t=0 时）设置为0，得出以下条件：

1.2 隐式静力学算法

工件成型基于拉格朗日法的平衡方程可表示为

式中，C是阻尼矩阵，fe是节点力等效矢量，fi是内力等效矢量，u是节点位移矢量。

在t和t+Δt时平衡方程分别为

进一步得到增量方程：

式中，k为常数。

进一步得到求解方程：

当步长Δfe很小时，u1=ut+Δt为显式求解算法。

当步长Δfe大时，不平衡力为ΔR，即

将fi(ut+Δt)表示成线性泰勒展开式：

得到近似解为

当ΔR很小时，可以得出t+Δt时刻的解ut+Δt，此时u1=ut+Δt为隐式静力学算法［17］。

ABAQUS是一种优秀的有限元软件之一，它具有力学强度分析、弹塑性分析等功能，广泛应用于机械、船舶和航空航天等领域。本研究使用的仿真软件是ABAQUS2016，其计算时调用的是隐式求解器模块（ABAQUS/Standard）和显式求解器模块（ABAQUS/Explicit），能求解线性、非线性和动力学问题。因此，文中基于上述显式动力学算法进行刷丝角度成型显式动力学计算，基于隐式静力学算法进行刷丝角度回弹隐式静力学计算，通过计算数据的传递可实现刷丝角度成型与回弹的无缝连接。

2 模型建立与网格划分

设定刷丝直径为0.6 mm、高为24 mm、长为13 mm、初始角度为90°，由Solidworks 软件对刷丝直径、长度和初始角度等其他参数按照实际尺寸进行建模。为节省时间并提高计算效率，本研究选用电刷板的单丝作为研究对象，截取电刷板一端3 mm 厚度进行研究，刷丝从其根部位置伸出长度为20 mm，对其中一侧刷丝进行有限元模拟。按照模型形状将其导入有限元软件中，选择0.2 mm 全局尺寸的二次四面体（C3D10M）网格进行划分，网格数量为10 124，如图1所示。

图1 电刷板刷丝三维模型和导电滑环实物图Fig.1 Three-dimensional model of the brush plate brush wire and physical diagram of the CSR

夹持板的作用是将刷丝偏转并成型一定的角度。夹持板的设计分为单侧偏转板、双侧短夹持板和双侧长夹持板。将单侧偏转板底部装配在刷丝右侧根部，刷丝表面与其一侧接触，刷丝单侧受力；对于双侧短夹持板，将刷丝头部进行夹紧，刷丝两侧分别与双侧短夹持板两侧接触，但不与根部接触；双侧长夹持板与双侧短夹持板的区别在于右侧受力面长度贴近刷丝根部，左侧受力面长度增加到刷丝根部2 mm 的距离。单侧偏转板设计高为22 mm，宽为1 mm；双侧短夹持板设计高为18 mm，宽为1 mm，夹持刷丝之间的距离为0.6 mm；双侧长夹持板设计与双侧短夹持板类似，区别在于其右侧高为22 mm，左侧高为20 mm。所有夹持板的一侧（左侧或右侧）厚度均为0.25 mm，均属于结构钢材料。本研究对夹持板进行了简化，如图2所示。

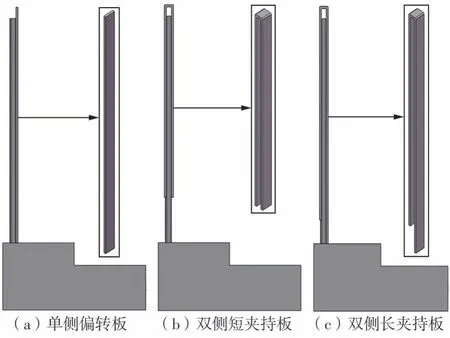
图2 夹持板示意图Fig.2 Diagram of the clamping plate

假设刷丝成型为悬臂梁受均布载荷作用的弯曲过程。安装方位如图2所示，定义刷丝右侧根部为偏转中心，对夹持板偏转角度进行设置。从夹持板的侧边施加大小为0.5 N 的圆周切向力，使其发生转动，再从刷丝根部进行角度的成型处理。由于成型角度过小时，刷丝应力和应变的变化不明显，且基本处于对称均匀分布状态，对刷丝的影响不大。故本研究模拟夹持板的偏转角度为115°、120°、125°时对刷丝角度成型的影响。

3 参数设置和边界条件

为了模拟刷丝角度成型过程，在边界条件中，对简化的电刷板进行完全固定约束，如图1（c）所示，定义夹持板和刷丝之间的接触类型为面到面接触，接触方法为罚函数方法；法相接触关系设置为硬接触，接触方法为罚函数方法。定义刷丝下端为接触主面，电刷板内部环道为接触从属面。在材料设置中，夹持板和电刷板定义为刚体，选用刷丝材料为AgNi10，该材料的导电性能优良，并具有很好的耐磨性能。刷丝在一定程度上属于金属线材细长杆，金属线材是一种各向同性材料，其弹塑性本构模型符合Von Mises 屈服准则。参考文献［18］中关于镍基合金在室温下的真实应力与应变值，当应变值为0.2、0.4、0.6和0.8时，应力分别为900、1 200、1 300 和1 400 MPa，并将此数值代入材料属性中。刷丝材料的各项力学性能参数如下：弹性模量为88 GPa、泊松比为0.37、密度为10.49 g/cm3、屈服应力为291 MPa。

为了模拟刷丝角度回弹过程，通过调整刷丝角度成型的模型进行回弹分析，删除夹持板及相应的接触条件和定义的载荷，保留电刷板固定约束条件，删除分析步中动力学分析的增量步，建立静力学分析步，进一步建立预定义场，将初始状态定义为刷丝角度成型后的受力状态，进行刷丝角度回弹的静力学分析。

4 刷丝角度成型与回弹分析

4.1 刷丝不同夹持方式的影响

为了更真实地模拟刷丝角度成型过程，将刷丝角度成型装置设置为一个偏转板。单侧偏转板的偏转角度为115°、120°、125°时对刷丝角度成型的影响如图3所示。

图3 单侧偏转板作用效果Fig.3 Effect of single-sided deflector plate

随着单侧偏转板偏转角度的增加，刷丝根部受到压力的作用最先产生变形，且变形量逐渐增大；刷丝另一侧与单侧偏转板逐渐产生分离，出现明显的翘曲，在偏转角为125°时单侧偏转板与刷丝几乎完全分离，加工效果非常差。

把单侧偏转板改为双侧短夹持板，分别在不同成型角度（115°、120°、125°）下进行有限元模拟，结果如图4所示。

图4 双侧短夹持板作用效果Fig.4 Effect of double-sided short clamping plate

随着双侧短夹持板偏转角度的增加，刷丝没有产生明显的翘曲现象，但刷丝受力不均，容易导致刷丝局部产生变形，无法保证刷丝在角度成型时的直线度，这会对刷丝本身的质量产生影响，影响刷丝与环片接触时压力的稳定性，对CSR信号的传递质量会产生一定的影响。综上所述，双侧短夹持板不能很好地保证刷丝成型的质量。

将双侧短夹持板改为双侧长夹持板，分别设置成型角度为115°、120°、125°，旋转幅值为平滑步分析，有限元模拟结果如图5所示。

随着双侧长夹持板偏转角度的增加，刷丝既没有产生翘曲现象，也没有产生受力不均现象。在角度成型过程中，刷丝与夹具接触面紧密贴合，刷丝受力均匀，而且应力变化明显集中在刷丝根部位置。可以看出，刷丝在角度成型阶段，双侧长夹持板具有良好的角度成型效果。

4.2 刷丝角度成型过程的有限元模拟

对刷丝在双侧长夹持板的成型角度为115°、120°、125°时进行有限元模拟，并对刷丝的应力和应变进行对比分析。由于刷丝主要受切向（X-Y截面）应力S22的作用，故截取刷丝X-Y截面方向中间层，其S22应力云图如图6所示。

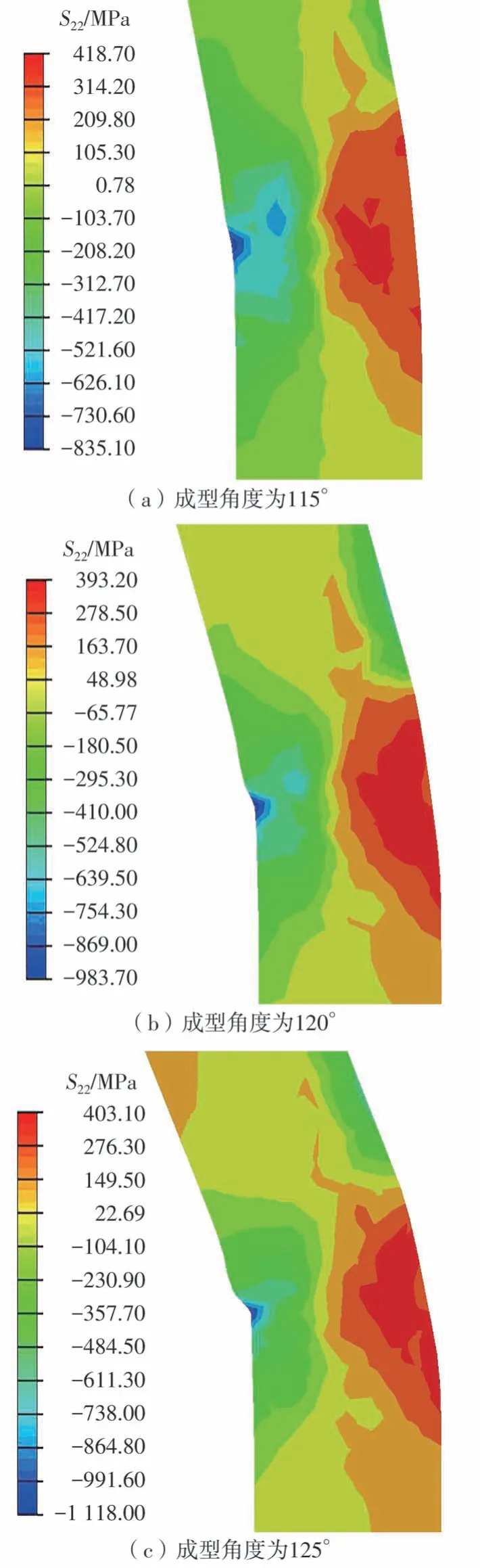
图6 刷丝角度成型过程应力云图Fig.6 Stress cloud diagram of brush wire angle forming process

随着成型角度的增加，刷丝在根部的左侧和右侧分别产生切向压应力和切向拉应力。成型角度从115°增大到125°时，刷丝右侧最大切向拉应力区域最先产生在中性层附近，并逐渐向右侧边缘扩展，在成型角度达到120°左右时最大切向拉应力区域已经扩展到刷丝右侧的表面位置，且切向拉应力值逐渐增大，切向拉应力最大值在393～419 MPa 之间，超过材料的屈服应力291 MPa，材料发生塑性变形；而刷丝左侧最大切向压应力区域最先产生在刷丝根部左侧位置，在成型角度为120°时最大切向压应力区域消退到刷丝左侧边缘处，且切向压应力最大值逐渐增大，其最大值在835～1 118 MPa 之间，超过材料的屈服应力291 MPa，材料发生塑性变形。

对刷丝中间层进行切片处理，得出刷丝在角度成型过程的切向应变云图，如图7所示。

图7 刷丝角度成型过程应变云图Fig.7 Strain cloud diagram of brush wire angle forming process

随着成型角度的增加，刷丝在根部的左侧和右侧材料分别产生切向压应变和切向拉应变。成型角度从115°增加到125°时，刷丝右侧切向拉应变区域较大，且切向拉应变最大值逐渐增大；刷丝左侧最大切向压应变区域逐渐减小，并逐渐向左侧边缘扩展，且切向压应变最大值逐渐增大，应变值主要集中在刷丝与电刷板的接触位置，切向压应变左侧位置开始发生挤压，刷丝左侧外壁逐渐增厚。

整个成型过程中，由于刷丝右侧与夹持板接触，刷丝右侧在夹持板受力面作用下抑制了刷丝应力的卸载。为防止夹持板偏转时夹紧面损伤电刷板，故将夹持板左侧夹紧面缩短2 mm。由于此区域材料堆积得不均匀，刷丝与电刷板根部的接触位置发生了一定的变形，形变逐渐增加，在成型角度增大到125°时刷丝左侧压应变区域已经发生了明显的凸起变形，这是因为缺少约束。综上所述，刷丝成型角度在120°以上时，应将夹持板左侧夹紧面尽量贴近刷丝左侧根部位置，保证刷丝角度成型的质量。

为更好地展示刷丝角度成型过程应变的变化趋势，对刷丝根部受力面选取4 个节点进行应变分析，截取刷丝根部X-Z方向截面。图8为刷丝应变根部节点选择示意图，其中节点1832 和1811 分别为刷丝外侧和内侧中性层附近单元，节点1825 和1842分别为刷丝最左侧和最右侧单元，4个节点的弯曲状态一致，具有很好的对比性。4 个节点的应变曲线如图9所示。

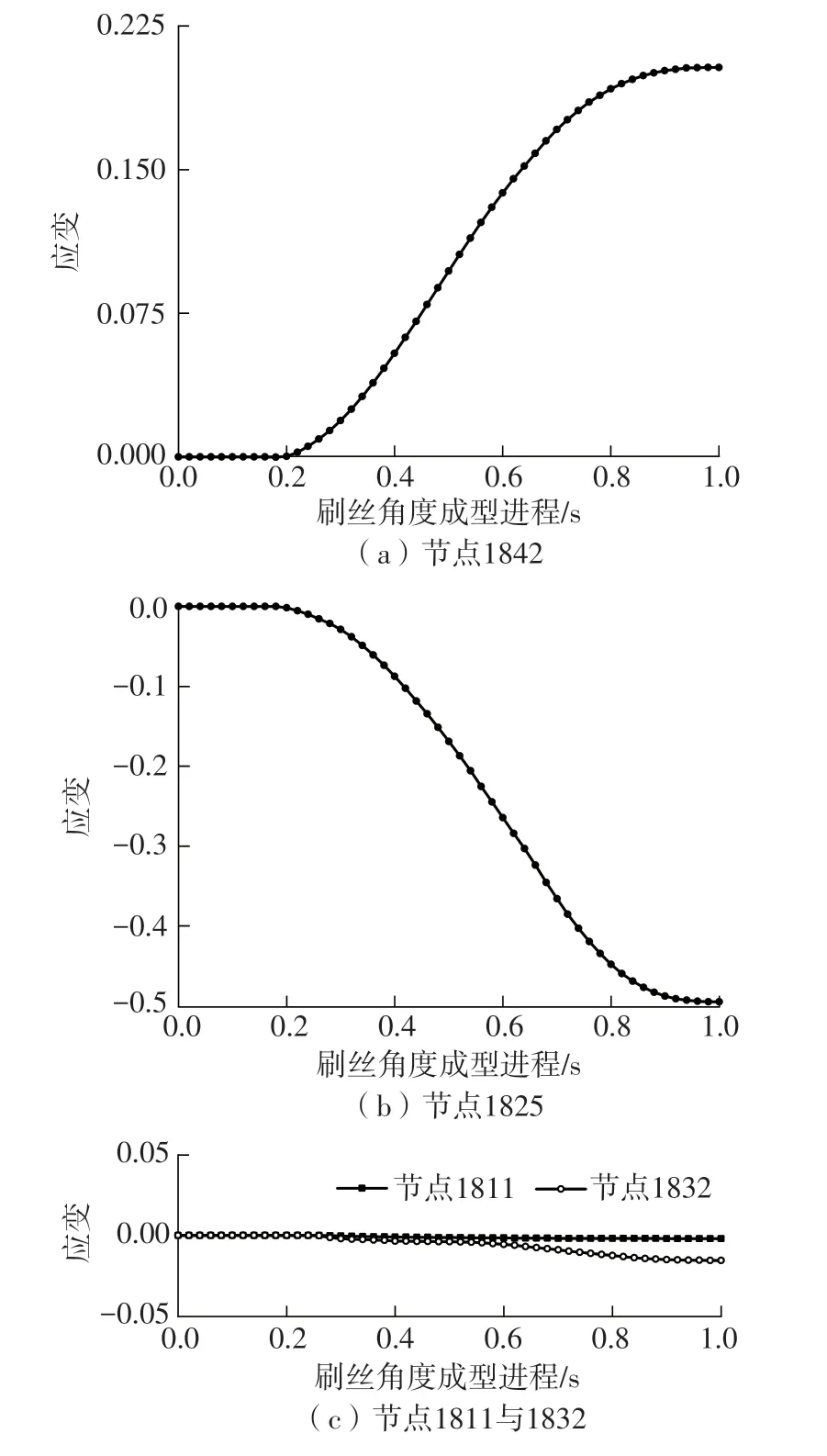
图9 4个节点的应变曲线Fig.9 Strain curves of four nodes

从图9（a）可知，节点1842 在受到拉应力作用时发生了拉伸变形，该节点材料的应变在前0.2 s内非常小，随着时间的推移，变形现象开始出现，应变在0.9 s 左右达到峰值，此后开始逐渐平稳，维持在稳定状态。

从图9（b）可知，在压应力的作用下，节点1825 发生了一定程度的压缩变形，在0.9 s 时应变达到最大值，此后保持在稳定状态。

从图9（c）可知，节点1832 由于压应力的作用发生了微小的压缩变形，节点1811 由于压应力作用较小，几乎没有变形产生。

综上所述，在刷丝角度成型的过程中，刷丝中性层的变化相对比较小，拉应力区域与压应力区域的变形平稳，最终都能处于稳定状态，进一步说明了双侧长夹持板的作用效果相对较好，能够更好地进行刷丝角度成型。

4.3 刷丝角度回弹过程的有限元模拟

根据刷丝在成型角度为115°、120°、125°时的模拟结果建立预定义场，并对刷丝回弹的过程进行S22切向（X-Y截面）应力和应变分析，结果如图10和图11所示。

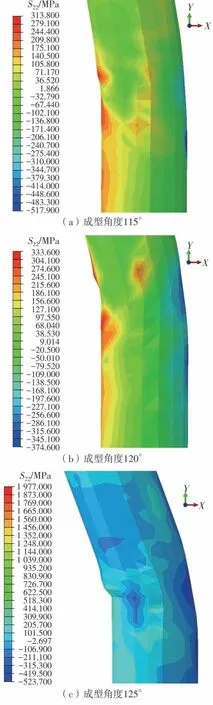
图10 刷丝角度回弹过程应力云图Fig.10 Stress cloud diagram of brush wire angle rebound process

图11 刷丝角度回弹过程应变云图Fig.11 Strain cloud diagram of brush wire angle rebound process

从图10 可知，随着成型角度的增加，刷丝回弹的切向拉应力与切向压应力区域逐渐增大。由于刷丝右侧在回弹过程中受到切向压应力的作用而呈现出切向压应力状态。当成型角度达到125°时，刷丝在回弹过程中的拉力逐渐释放，切向压应力逐渐增大并扩展到刷丝整个表面。切向压应力最大值在375～524 MPa 之间，材料的残余应力逐渐增大，超过材料的屈服应力291 MPa，回弹过程发生弹塑性变形。随着成型角度的增加，由于刷丝左侧在回弹过程中受到切向拉应力的作用而呈现出切向拉应力状态。当成型角度达到125°时，由于拉力已经释放，切向拉应力最大值达到1 977 MPa，残余应力过大，远远超过材料的屈服应力291 MPa，所以材料发生弹塑性变形的同时，刷丝材料左侧根部位置也很可能发生破坏。

从图11 可知，随着成型角度的增加，刷丝的切向应变值逐渐增大，刷丝塑性变形也随之增大。从成型角度115°开始，刷丝左侧发生了局部的凸起变形，并且随着刷丝成型角度的增加，这个局部变形逐渐增大。

整个回弹过程中，刷丝存在残余应力，并且发生弹塑性变形，在成型角度为125°时变形达到最大。由于刷丝左侧根部位置受到电刷板的挤压作用而发生局部变形，虽然变形量相对较大，但仍然没有消除成型过程中变形的影响。因此，本研究刷丝成型与回弹的模拟结果进一步说明，刷丝的回弹角度与成型角度呈正相关，即刷丝的成型角度越大，刷丝成型后的回弹变形值越大。刷丝成型角度在120°以上时，为了防止刷丝在发生弹塑性变形时其材料左侧根部发生破坏，应将夹持板左侧夹紧面尽量贴近刷丝左侧根部位置，保证刷丝角度成型的质量。

如图12 所示，以电刷板夹紧部分竖直方向的刷丝为基准，测量刷丝的回弹角度。从刷丝右侧面上中线位置分别提取4 个节点，其中节点2611 和9672 为刷丝的成型角度部分，节点8876 和7811 为刷丝在电刷板夹紧水平的部分。通过在ABAQUS中查询这4个节点的坐标位置，可分别得到刷丝的成型角度直线和水平部分直线，计算两直线之间的夹角，获得回弹后的实际角度θ，回弹后角度与成型角度的差值即为刷丝的回弹角度。

图12 刷丝回弹角度计算方法示意图Fig.12 Schematic diagram of brush wire rebound angle calculation

按照上述对刷丝角度成型后回弹角度的计算方法，分别对刷丝回弹后的节点坐标进行查询，并计算回弹角度，此时刷丝的成型角度为图12中的θ。为对有限元法计算的结果进行验证分析，文献［19］将线材回弹理论计算结果和试验结果进行了对比分析，发现最大误差为0.36°。因此，该线材回弹角度计算方法可作为理论计算方法，计算公式为

式中，θ为刷丝的成型角度，M为弯曲力矩，r为刷丝的弯曲半径，σs为刷丝的屈服应力，E为弹性模量［18］。

将文献［19］中ABAQUS有限元分析结果与理论公式计算结果进行比较，发现最大误差角为0.12°，说明用ABAQUS有限元软件分析材料模型的成型与回弹的结果是正确且可靠的，可为本研究模型的分析提供理论支持。将本研究的刷丝各项参数代入式（18）中，计算出刷丝的回弹理论值，具体回弹仿真值与理论值如表1所示。

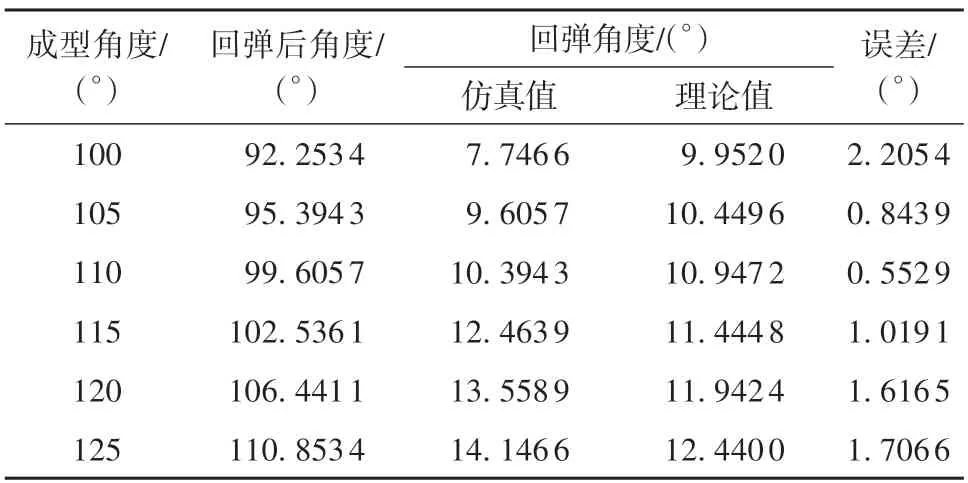
表1 刷丝回弹仿真值与理论值Table 1 Simulated and theoretical values of brush wire rebound

从表中可以看出，基于有限元法的刷丝回弹仿真结果与理论计算结果有一定的误差，这是由于理论计算结果并没有考虑刷丝与夹持板之间的摩擦作用。而在本研究的有限元模拟中添加了接触摩擦，所以理论值与仿真值有一定的偏差。如图13所示，刷丝回弹角度的最大相对误差约为2°，但平均误差值在1°左右，总体看来回弹趋势基本一致，可以很好地表示出刷丝回弹角度的变化规律。

图13 刷丝回弹角对比Fig.13 Rebound angle comparison of brush wire

5 结论

文中通过模拟夹持板的偏转角度为115°、120°、125°时对刷丝角度成型的影响，确定了刷丝角度的成型方式，揭示了有限元法模拟刷丝角度成型和回弹的过程，并对刷丝角度回弹的理论值与仿真值进行了对比分析，得出以下结论：

（1）与单侧偏转板和双侧短夹持板相比，双侧长夹持板对刷丝角度成型的作用效果最佳。对刷丝根部受力面选取4个节点进行应变分析，发现刷丝最终都能处于一种稳定的状态，进一步说明了双侧长夹持板的作用效果相对较好，能够很好地进行刷丝角度的成型。

（2）从整个过程应力和应变的模拟结果可知，刷丝的回弹角度与成型角度呈正相关，即刷丝的成型角度越大，刷丝成型后的回弹变形值越大。刷丝成型角度在120°以上时，为了防止刷丝在发生弹塑性变形时其材料左侧根部发生破坏，应将夹持板左侧夹紧面尽量贴近刷丝左侧根部位置，保证刷丝角度成型的质量。

（3）将刷丝回弹的仿真值与理论值进行对比分析，发现刷丝回弹角度的平均误差在1°左右，总体回弹趋势基本一致。因此，在生产批量不大且无需连续加工的情况下，此方法既简单又实用，可为导电滑环刷丝的工装及设计提供一定的技术支持。