基于贝叶斯神经网络的金属材料P-S-N 曲线估计

杨旭锋 刘泽清 张懿

（西南交通大学 机械工程学院，四川 成都 610031）

获取材料的疲劳寿命与外加应力或应变之间的关系是结构疲劳寿命分析的基础和关键。1910 年，由国外学者提出的方程lgN=β0+β1lgS，给出了对数疲劳寿命（N）与对数应力水平（S）之间的线性关系。为了描述当应力水平低于疲劳极限S0时，疲劳寿命趋于无穷大的现象，1914年Stromeyer［1］提出了非线性S-N模型。根据疲劳试验数据，拟合出S-N曲线，一直是工程领域开展疲劳寿命分析所广泛使用的手段。近年来，神经网络模型被广泛用于建立疲劳寿命模型。Mathur等［2］证明了神经网络预测疲劳寿命的能力。Troudet等［3］提出了一种前馈神经网络，用以实时评估机械应力作用下构件的退化情况并预测构件最终失效循环次数。Artymiak 等［4］训练了4个多层前馈神经网络，用以构建S-N曲线。Vassilopoulos 等［5］利用前馈神经网络构建恒定寿命图，用以预测疲劳寿命。温海骏等［6］采用粒子群算法优化的神经网络对再制造工件进行疲劳寿命预测，为实现再制造工件的疲劳寿命预测提供了一种新的方法。胡贇等［7］提出了一种疲劳寿命服从对数正态分布的疲劳强度概率分布数值模拟方法，该方法能够精确地估计材料的P-S-N（失效概率-应力-循环次数）曲线。由于疲劳失效机理复杂，疲劳试验数据往往呈现出较大的分散性，因此，采用P-S-N曲线描述应力与疲劳寿命之间的关系更为恰当。长期以来，众多研究人员一直致力于疲劳试验技术与拟合方法的研究。但由于疲劳试验所需成本高且耗时，疲劳试验数据往往较少，因此如何通过少量的试验数据获得可靠的P-S-N曲线，成为人们主要关注的问题。

迄今，人们提出了多种方法用以估计材料的P-S-N曲线。总体而言，可将其归为两大类：传统方法和机器学习方法。在传统方法方面，Ling 等［8］建立了估计P-S-N曲线的最大似然方法（MLE）；赵永翔等［9］将经典极大似然法拓展到Langer 模型，提出了估计三参数、Langer 和Basquin 常用的疲劳应力-寿命模型P-S-N曲线及其置信区间的统一方法；Klemenc 等［10］采用蚁群算法估计三参数，提出了一种快速估计S-N曲线及其分散性的方法；Xie 等［11］基于失效轨迹概念和向后统计推断技术，提出了一种用少量试验数据拟合P-S-N曲线的方法；刘潇然等［12］基于非嵌入式多项式混沌展开及贝叶斯更新方法，提出了一种中等寿命区的P-S-N曲线小子样预测方法。在机器学习方法方面，文献［13-14］提出了基于贝叶斯模型的疲劳数据分析方法；Liu 等［15］提出了用于P-S-N曲线估计的分层贝叶斯模型；Chen等［16］基于贝叶斯数据扩展与分层贝叶斯模型，提出了一种用于稀疏样本的P-S-N曲线拟合方法；Chen等［17］提出了一种基于概率的物理驱动神经网络（PPgNN）模型，用于疲劳数据的分析。尽管估计P-S-N曲线的方法众多，但由于疲劳失效机制复杂，材料疲劳试验数据较少，这使得至今为止P-S-N曲线的确定仍是一个尚未解决的问题。

20 世纪90 年代，基于不确定性预测理论的贝叶斯神经网络（BNN）模型被提出。文献［18-19］详细介绍了BNN 的基本原理，其中心思想在于：根据给定的先验分布，利用贝叶斯定理描述神经网络权重参数的不确定性，再从样本数据中获得后验概率分布。相较于传统神经网络，BNN 不仅可以对结果进行预测，还可以对预测结果进行不确定性量化，从而有效地解决神经网络模型的过拟合问题。目前，BNN 模型已经在流体力学中的流场预测［20］、匀质化复合材料参数预测［21］、多孔介质中多相流预测［22］、铁路客流量预测［23］等领域得到了应用，但其在材料疲劳性能不确定性量化领域中的应用尚未开始。

为此，文中提出了基于BNN 模型的金属材料P-S-N曲线估计方法。目前，在BNN 模型中，大多采用基于Kullback-Leibler（KL）散度的变分推理方法（BBP算法）对权重参数的后验分布进行求解，但BBP算法在处理复杂后验分布时，容易低估参数的分散性，从而导致BNN 模型给出不合理的疲劳数据预测结果。为此，文中引入基于α散度的黑盒（BB-α）算法［24］对权重参数进行后验估计，以提高P-S-N曲线的预测精度。最后，基于已有的试验数据，使用提出的方法对2524-T3铝合金、2024-T4铝合金和S420MC 钢的P-S-N曲线进行了拟合，以验证所提方法的可行性。

1 贝叶斯神经网络模型

1.1 贝叶斯神经网络基本原理

给定一个观测数据集D(x，y)，x=(x1，x2，…，xn)为输入样本集，y=(y1，y2，…，yn)为输出样本集。神经网络的权重参数用ω=(ω1，ω2，…，ωd)表示，可以将神经网络模型表示为f ω，该模型通过最小化损失函数L(f ω(x)，y)来找到合适的权重参数ω，这里的ω为定值，如图1（a）所示。不同于传统神经网络模型，BNN 模型的权重参数不再是一个确定的值，而是一个概率分布，如图1（b）所示。它将贝叶斯方法与神经网络结合起来，既能给出预测结果，也能给出预测结果的误差。

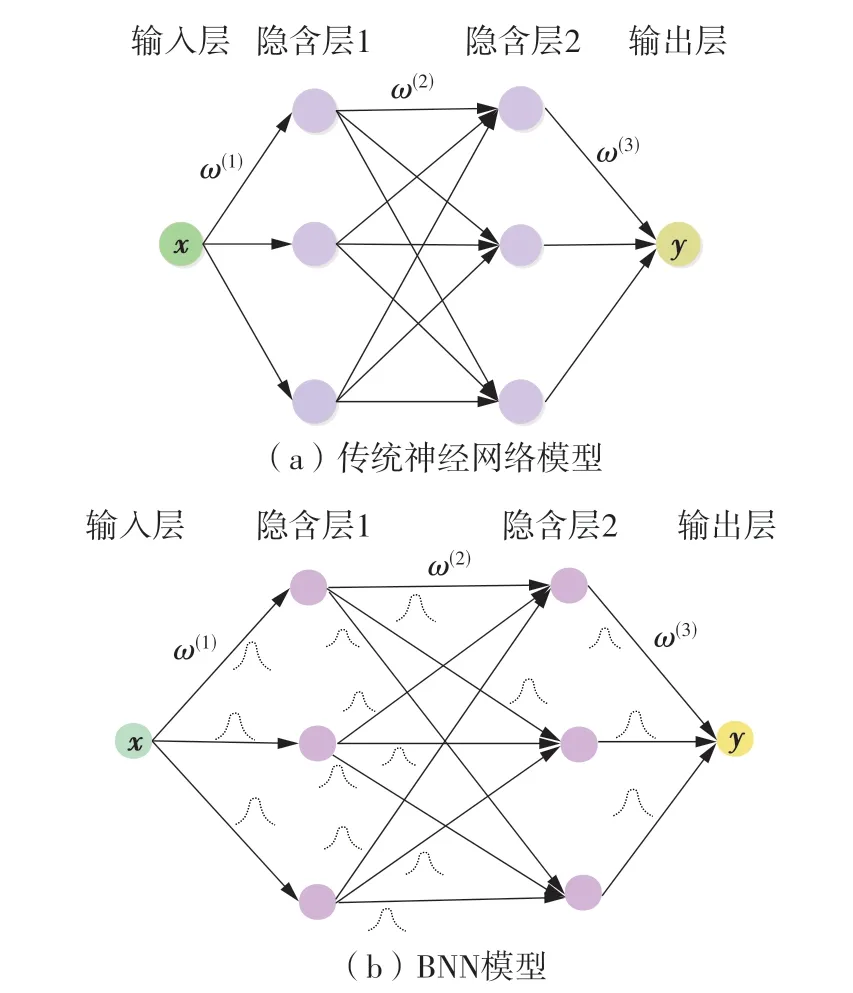
图1 传统神经网络模型与BNN模型的结构Fig.1 Structures of traditional neural network model and BNN model

BNN采用高斯随机过程来描述输入与输出之间的关系，即

式中，p(·)为概率密度函数，f ω(x)为均值，为方差。

假定观测样本D相互独立，则整个数据集的似然函数可以表示为

BNN的训练目标是找到ω的后验分布p(ω|D)。根据贝叶斯定理，权重参数的后验分布可以表示为

式中，p(ω)为参数的先验分布，p(D|ω)为观测数据的似然函数。

给定一个新的输入x*时，可以得到输出y*的预测分布：

假设后验分布p(ω|D)已得到，则可以根据蒙特卡洛法的思想对ω进行多次采样，计算确定性的f ω(x*)，然后多次计算取平均，可以得到预测结果的期望值［21］：

同理，还可以得到预测结果的方差：

1.2 贝叶斯变分推理

由式（4）可知，求解后验分布p(ω|D)是BNN开展预测的关键。然而，由于神经网络模型的权重参数较多（俗称“维数灾难”），通过直接积分或马尔可夫链（MCMC）采样来求解p(ω|D)是难以实现的。因此，在BNN 模型中，通常采用变分推理的策略，如BBP算法和BB-α算法。

1.2.1 BBP算法

BBP 算法的基本思想是用一个新的分布q(θ；ω)去逼近后验分布p(ω|D)，把求解后验分布的问题转化为关于参数θ的优化问题。选择q(θ；ω)为一个d项连乘的高斯分布：

式中，θ=(μi，σi)，i=1，2，…，d。然后将式（4）中的后验分布p(ω|D)替换为q(θ；ω)，可得

接下来，如何使新的分布q(θ；ω)尽可能地接近真实的后验分布p(ω|D)，则成为了关键问题。通常用KL散度［25］来衡量两个分布之间的差异。KL散度值越小，说明两个分布之间的差异越小，反之则越大。因此，要使两个分布接近，优化目标即变成了寻找最优的使得KL散度值最小，即

式中，Eq(·)表示关于分布q(θ；ω)的期望。

1.2.2 BB-α算法

BBP 算法通过参数化的连乘高斯分布来近似p(ω|D)，并通过最小化KL散度获取最优的参数θ。研究表明［24］，当后验分布为多峰分布或权重之间存在相关性时，BBP 算法容易低估参数的分散性，从而导致神经网络给出不合理的预测。为此，文献［24］提出了BB-α算法。

BB-α算法是一种基于α散度最小化的近似推理方法。与KL 散度类似，α散度也可用来衡量两个分布之间的差异，其定义为

KL 散度可以看作α散度的特殊形式。通过改变α值可以得到不同的KL 散度值，进而产生分散程度不同的后验分布预测结果。与BBP 算法不同，BB-α算法采用指数族分布对后验分布进行近似。

由于后验分布p(ω|D) ∝故BB-α算法将q(θ；ω)构造为与p(ω|D)类似的连乘积形式，即

式中：θ=(θ0，θ1，…，θn)；g(θi；ω)与g（0θ0；ω）从指数分布族选取，

θ0和θi为指数分布的自然参数，s(ω)为充分统计量，Z(θ0)为正则化常数。则BB-α算法的优化目标为

2 算例分析

2.1 问题描述

文中采用3 个算例对BNN 模型预测P-S-N曲线的有效性进行验证。每个算例中，均将基于BBP算法的BNN（BNN-BBP）模型和基于BB-α算法的BNN（BNN-BB-α）模型的估计结果进行对比，以验证BB-α算法的优势。同时，为了体现BNN-BB-α的优势，每个算例中均将其与传统MLE方法［8］以及当前较为先进的PPgNN方法［17］进行对比。

MLE构造了一个包含4个参数的疲劳寿命概率密度函数，而后根据疲劳数据，采用最大似然估计方法对未知参数进行求解。PPgNN与传统神经网络的不同之处在于：传统的神经网络以某一应力水平下的寿命为预测目标；PPgNN假定对数空间中的疲劳寿命服从正态分布，以正态分布的分布参数作为神经网络的输出，从而使神经网络能够对S-N曲线的概率特性进行预测。此外，PPgNN在损失函数中引入了材料P-S-N曲线变化的物理规律（①疲劳寿命的标准差一般随应力的减小而增大；②疲劳曲线的曲率随着应力的减小而减小，且如果材料没有明显的疲劳极限，则在疲劳极限附近表现出非常长的寿命），从而使预测结果更加符合人们的物理认知。

算例1 是在4 个应力水平下对2524-T3 铝合金的标准试样进行疲劳试验，每个应力水平进行约15次试验，共计59个试验数据［11］，详见表1。

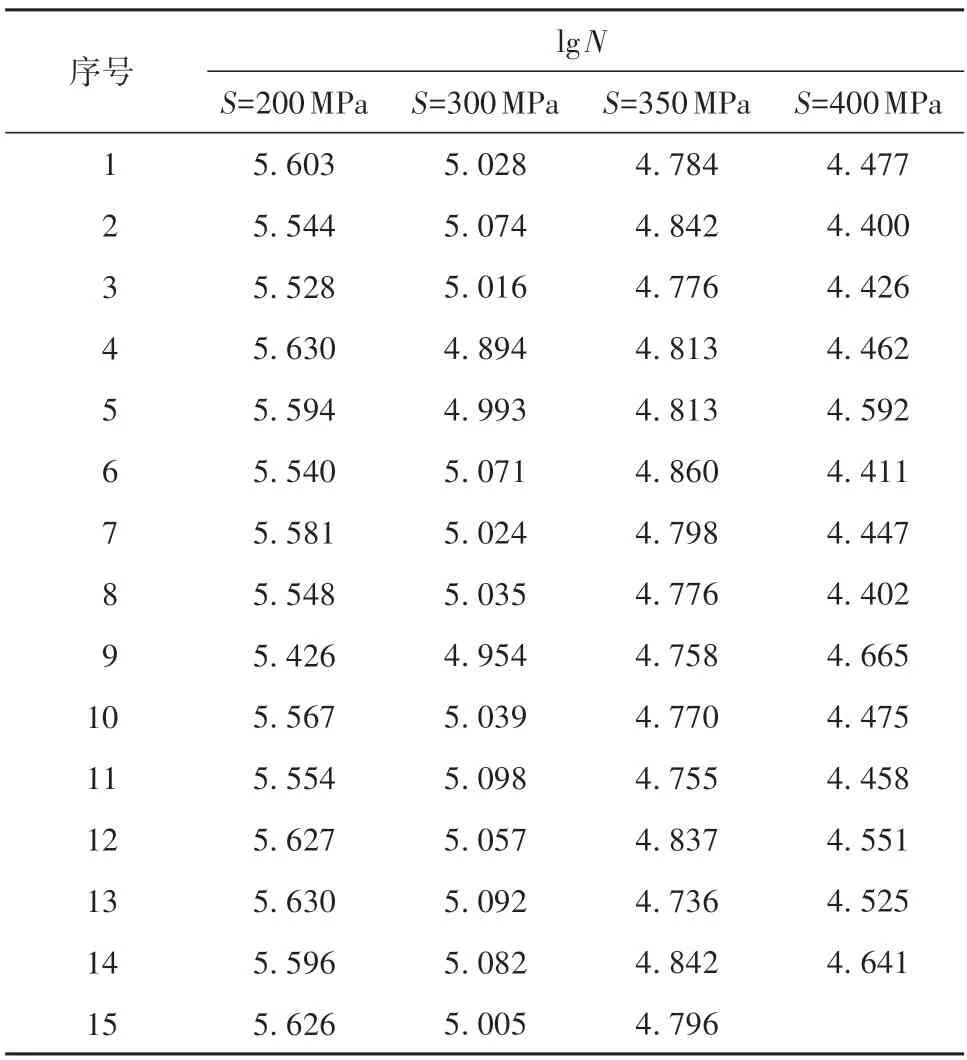
表1 2524-T3铝合金的疲劳寿命试验数据Table 1 Fatigue life test data of 2524-T3 aluminum alloy

算例2 是在9 个应力水平下对2024-T4 铝合金的标准试样进行疲劳试验，每个应力水平进行约30次试验，共计252个试验数据［26］，详见表2。

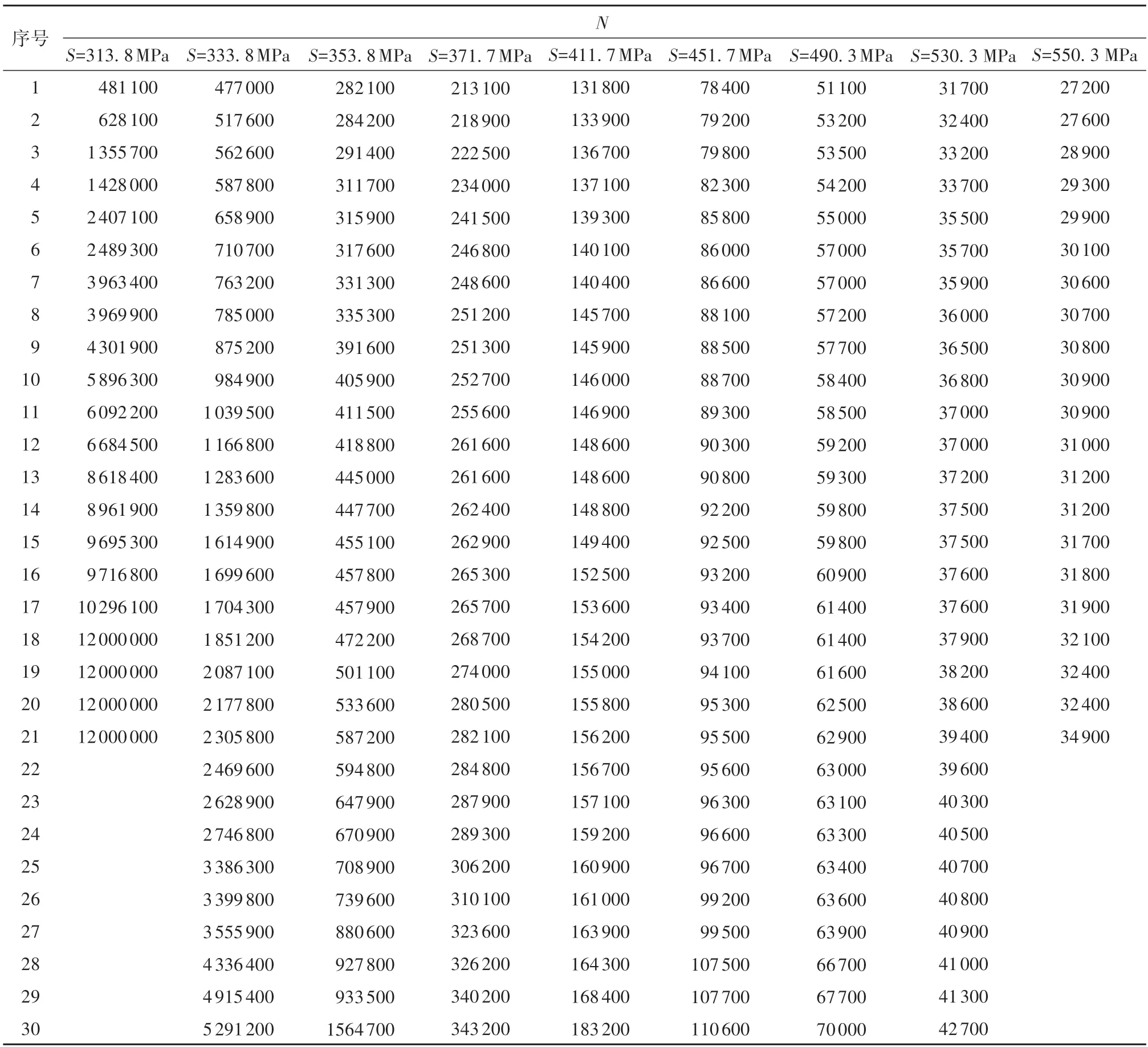
表2 2024-T4铝合金的疲劳寿命试验数据Table 2 Fatigue life test data of 2024-T4 aluminum alloy

算例3 是对S420MC 钢板切割的扁平试样进行疲劳试验，试验结束后，统计共有65 个试样发生断裂，剩余的15个试样在200万次载荷循环中未发生破坏［10］。仅使用断裂试样的试验数据来估计S-N曲线及其疲劳寿命分布特性，试验数据详见表3。

2.2 疲劳数据的BNN模型建立

在建立疲劳寿命预测模型前，需要对疲劳数据进行处理。首先，文中采用MaxAbsScaler 函数对3 个算例的数据集进行归一化，训练完成后再将数据进行反归一化，得到实际值。MaxAbsScaler 是根据数据集中的最大绝对值来缩放和平移每个特征，不会移动数据的中心，因此不会影响数据的疏密性，其在文献［27-29］中表现出了较好的性能。文中模型的输入样本集X为应力，对其进行归一化，得到

式中，X'为归一化后的值，|Xmax|为X的最大绝对值。

输出样本集Y为疲劳寿命。由于文中疲劳寿命的数量级在104～108之间，差距较大，因此在对疲劳寿命进行归一化前先取对数，即

式中，Y0为疲劳寿命取对数的值，|Y0，max|为Y0的最大绝对值，Y'0为归一化后的值。

接着，对数据集进行划分。通常情况下，选取数据集总量的80%作为训练集，剩余的作为测试集［30-32］。

BNN模型由输入层、隐含层和输出层构成，隐含层的层数和层中神经元的数量是可以调整的，每个隐含层的神经元数量在5～100之间［33］。文中隐含层神经元采用双曲正切（tanh）激活函数。BNN-BBP和BNN-BB-α模型有着相同的参数设置：学习率为0.000 5；迭代次数（epoch）为10 万；对于隐含层及神经元数，2524-T3 铝合金的为5-5，2024-T4 铝合金、S420MC 钢的则为5-5-5。对于BB-α算法，α的取值在0～1之间，文中将α设置为0.5。

2.3 预测结果与分析

图2 给出了BNN-BB-α模型对3 种材料的P-S-N估计曲线及概率密度曲面。从图中可以看出不同应力水平下疲劳寿命的概率密度函数变化情况，也可以求出每个位置处对应的概率密度函数值。同时，为了说明基于BB-α的BNN 训练过程的收敛性及采用其预测的可靠度，图3给出了3个算例的损失函数（见式（15））收敛曲线。从图中可以看出，采用该损失函数训练的BNN 具有良好的收敛性。图4 为BNN-BB-α模型对测试集的预测结果，黑色虚线间表示两倍误差带。可以看出，对于2524-T3铝合金、2024-T4铝合金和S420MC钢，其预测结果落入两倍误差带的占比分别为100%、92%、92%，这表明

图2 BNN-BB-α模型的疲劳寿命概率分布曲线Fig.2 Fatigue life probability distribution curves of BNN-BB-α model

图3 BNN-BB-α模型的损失函数收敛曲线Fig.3 Loss function converging curves of BNN-BB-α model

图4 BNN-BB-α模型对测试集的预测结果Fig.4 Prediction results of BNN-BB-α model for test set

BNN-BB-α模型在预测S-N曲线时具有较高的精度。

BNN-BB-α与BNN-BBP模型对3种材料的P-S-N估计性能比较如图5所示。从图中可以发现：在网络参数设定相同的情况下，采用BNN-BB-α模型得到的估计结果比采用BNN-BBP模型得到的估计结果要好，尤其是在对分散性较大的数据进行估计时，BNN-BB-α模型的优势更加明显。对于算例2，从图5（b）可知，当应力小于370 MPa时，使用BBP算法的预测效果较差。对于算例3，从图5（c）可以看出，使用BNN-BBP 模型进行估计时，各个应力水平下寿命的分散性均被低估。另外，算例2 中，对2024-T4铝合金在多个应力水平下开展了疲劳试验，得到了各个应力水平下的疲劳试验数据，这些数据较为完整地描述了2024-T4 铝合金的疲劳性能演化过程：随着应力水平的降低，疲劳寿命逐渐变长，其分散性也逐渐变大。文中提出的方法依据试验数据，能较好地预测出这一变化趋势。

图5 BNN-BB-α与BNN-BBP模型对3种材料的P-S-N估计性能比较Fig.5 Comparison of P-S-N estimation performance between BNN-BB-α and BNN-BBP models for three materials

为进一步验证所提方法的有效性，文中将BNN-BB-α与MLE 和PPgNN 模型对3 种材料的P-S-N估计性能进行了比较，结果如图6、图7 所示。从图6 可以发现，采用BNN-BB-α模型估计疲劳数据的P-S-N曲线具有更大的优势：MLE 模型可能会受局部统计参量的影响而给出非安全估计，较多的试验数据落在了95%置信区间外；BNN-BB-α模型则能给出相对保守的估计结果，在疲劳试验数据较少时仍可获得较为保守的95%置信区间（见图6（a））。

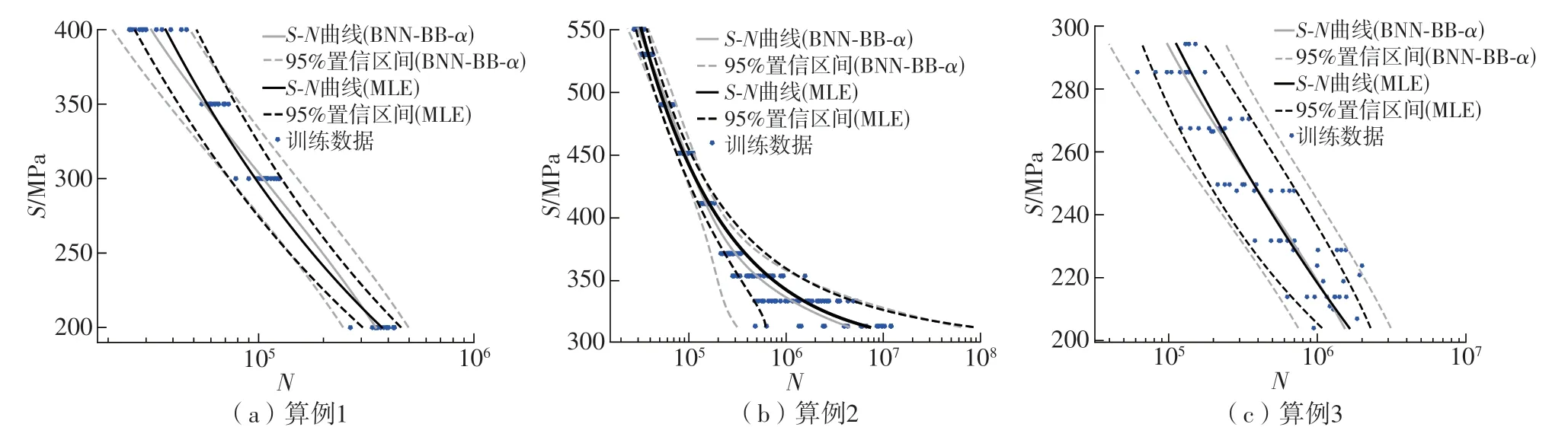
图6 BNN-BB-α与MLE模型对3种材料的P-S-N估计性能比较Fig.6 Comparison of P-S-N estimation performance between BNN-BB-α and MLE models for three materials

图7 BNN-BB-α与PPgNN模型对3种材料的P-S-N估计性能比较Fig.7 Comparison of P-S-N estimation performance between BNN-BB-α and PPgNN models for three materials

从图7 可以发现，相比于PPgNN 模型，BNNBB-α模型显示了更好的包络性。对于算例1，在应力水平为200 MPa 和400 MPa 时，BNN-BB-α模型的疲劳寿命不确定性要稍大于PPgNN模型。对于算例2，PPgNN 模型的疲劳寿命不确定性比BNN-BB-α模型稍低，其中252 个疲劳数据中，有12 个落于包络线外。采用4 种方法对3 种材料的疲劳寿命进行预测时，3个算例的预测值落入95%置信区间的占比和训练时间如表4 所示。从表中可以看出：采用BNN-BB-α模型得到的P-S-N曲线包络性最佳，即绝大部分数据点都落入估计曲线内；BNN-BB-α 模型的用时比BNN-BBP 模型短，比MLE 和PPgNN 模型长，但在可接受的范围内。

表4 3个算例的预测值落入95%置信区间的占比和训练时间Table 4 Proportions of predictive values falling into 95% confidence interval and training time of three examples

为了展现参数α对BNN-BB-α模型预测结果的影响，文中对不同α值的预测结果进行了对比，不同α值下BNN-BB-α模型预测的95%置信区间如图8 所示，不同α值和不同应力下BNN-BB-α模型的预测均值和标准差如图9 所示。从图中可以发现，α值对预测均值的影响较小，但对预测标准差的影响明显。总体来看，当α值增大时，各个应力水平下的预测标准差增大，即估计不确定性增加。过小的标准差，意味着预测太过激进；过大的标准差，意味着预测结果太过保守。总的来说，当α取0.5 时估计效果最好，此时BNN-BB-α模型的95%置信区间能够恰好包络足够多的疲劳数据。

图8 α取不同值时BNN-BB-α模型的95%置信区间估计Fig.8 Estimation of 95% confidence interval of BNN-BB-α with different values of α

图9 不同α值和不同应力下BNN-BB-α模型的预测结果Fig.9 Prediction results of BNN-BB-α model at different values of α and different stress levels

3 结论

材料的疲劳-寿命曲线具有较大的分散性，获取材料的P-S-N曲线具有重要的意义。文中提出了一种基于BNN 模型的金属材料疲劳试验数据分析方法。该方法将传统神经网络模型的权重参数视为随机变量，采用贝叶斯参数估计方法对其后验分布规律进行求解。考虑到已有基于KL 散度的变分推理方法容易低估权重参数的不确定性，文中引入了基于α散度的BB-α算法，并通过3 个算例对基于BNN模型的P-S-N曲线拟合方法的性能进行了验证，得到以下结论：

（1）BNN-BB-α模型的估计效果优于BNN-BBP模型，尤其是对分散性较大的数据集进行估计时，优势更为明显。BNN-BBP 模型容易低估数据的分散性，而BNN-BB-α模型则能给出较为保守的估计结果。采用α散度度量代替KL 散度度量后，对疲劳数据的估计效果得到提升。当α=0.5 时，BNNBB-α模型的估计效果最佳。

（2）相比于MLE 和PPgNN 模型，BNN-BB-α模型的包络性更好，疲劳数据能够更多地落于95%置信区间内；BNN-BB-α可以获得更加保守、准确的P-S-N曲线估计结果，这在工程实际中具有重要的意义。

（3）BNN-BB-α模型的计算速度比MLE 和PPgNN 模型慢，所需要时间相差100 s 左右，这在实际工程中是完全可以接受的。