直扩超声波宽带体内通信的误比特率仿真研究

刘娇蛟 陈阿粤 马碧云

（华南理工大学 电子与信息学院，广东 广州 510640）

随着我国老龄化趋势的加剧，传统医疗服务模式已不能适应时代的需求。自2014 年起，我国颁布了多项政策大力支持远程医疗［1］，推广远程医疗被纳入我国第十四个五年计划和2035年远景目标。体域网是实现远程医疗的重要组成部分，采用人体通信技术把体内、体表和人体周围的传感器、便携式终端等连接起来。其中，植入式节点可以直接采集人体内部的生理数据，用于心脏起搏、胰岛素监测、神经系统监测等领域，可以助推远程健康监测和疾病预防，避免重症疾病的发生，缓解医疗资源紧缺的矛盾，具有重要的社会意义。

人体通信技术大多采用射频（RF）电磁波传输信号。然而，在含水量高达65%的人体软组织中，电磁波衰减快，易被体内水分吸收并产生热量，温度过高时将有损人体细胞。世界卫生组织认为暴露在电磁辐射下的人体会增加患癌风险［2］。现有研究表明，2.5 GHz的RF电磁波在肌肉中传输10～29 cm时功率衰减约75～130 dB，但1 MHz 超声波的功率衰减仅为10～20 dB［3］。过去几十年的医学临床诊断表明，超声波在一定功率下对人体无害，可避免同频段电磁干扰。

因此，超声人体通信逐渐引起学者的关注［4］。现有针对植入式节点的超声波体内通信技术可以分为两类：一类是有载波通信，包括PSK［5］、OOK［6］、OOK-FDM［7］、OFDM［8］和QAM［9］等，文献［5］提出了采用传感器阵列的空间自由度来提高通信速率的方法；另一类是无载波通信，如超声波宽带技术［10］（UsWB），通过发射极短的超声波脉冲携带信息，具有占空比低和能耗低的特点，可以结合跳时与脉冲位置调制（PPM）进行多点接入。文献［11］提出了医学物联网方案，低功耗UsWB 的通信速率可达180 kb/s。文献［12］通过直接序列扩频技术来提高多点通信的抗干扰能力，相同信噪比下直扩超声波宽带（DS-UsWB）通信可采用较短的帧长和码长以获得更低的误码率，但该文献假设脉冲宽度极短，可以忽略多径干扰，因而对换能器的带宽要求很高。

现有研究大都试图提高超声波体内通信的速率。如采用OFDM技术实现超声波体内通信的速率可达12.09 Mb/s，但误比特率（BER）为1.9×10-4，不能满足体内信息传输的可靠性要求［13］。然而，超声人体信道具有密集多径的特性，人体内包括不同器官和组织，其大小、密度和其中的声速不尽相同，超声波在体内传播时会产生反射和散射等现象，接收信号是发射信号经过各种衰减和时延的多路信号叠加，多径时延具有密集特性，最小间隔约几百纳秒［14-15］，其特性不同于现有的射频通信信道。

如果脉冲宽度小于多径时延间隔的最小值，采用极短脉冲的DS-UsWB 通信技术可避免多径交叠及其带来的干扰。然而，由于人体的呼吸、肠胃蠕动、肢体活动等，体内外节点存在不对齐现象。为了保证信号接收，实际应用中需要采用方向角足够大的超声探头，但大方向角的超宽带超声探头难以实现，实际探头产生的脉冲宽度不够小，在接收端会产生多径交叠，对信号判决产生干扰。目前，对体内超声人体信道的多径分布及其对通信影响的研究较少。为了探究密集多径下体内超声通信的可靠性，文中借助超声人体信道的三维建模和超声波体内通信仿真，对超声人体信道的多径时延统计特性进行了定量分析，推导了DS-UsWB 体内通信的多径干扰和BER下界，以期为调整扩频码长实现可靠体内通信提供理论依据。

1 多径信道相对时延的统计特性

超声波在体内传播的速度慢且衰减小，经过不同组织产生的反射和散色强度不同，信道特性的多径分布和时延扩展具有特殊性，现有射频通信的无线信道模型不能直接使用。

文中采用超声人体信道的三维建模和信道冲激响应测试获得多径信道的相对时延统计特性。k-Wave 是Matlab 声学仿真工具箱，最初由 Treeby等［16］设计和开发，采用数值计算方法对超声波在生物组织中的传播进行建模和仿真，可用于体内超声通信信道建模［17］和光声成像仿真［18］等领域。

1.1 体内超声波传播原理

当超声波在体内软组织中传播时，会存在压力、密度、温度和粒子速度的动态波动，这些变化可以采用3个耦合的一阶偏微分方程描述，即运动方程、连续性方程和状态方程［19］。那么，超声波在体内的传播方程可以表示为

式中，p(x，y，z，t)是空间和时间的声压场，v是超声波在人体软组织中的传播速度。当超声波在体内传播时，会被人体组织吸收一部分能量，导致初始压力p0降到p(d)，

式中：d是超声波在介质中的传播距离；α是超声波束的能量耗散系数，与载波频率有关，α=af b，a和b分别是声波衰减系数和吸收因子，其取值与人体组织有关，不同组织的能量耗散系数和衰减系数不同。

可见，根据式（1）、（2）可以获得设定时间范围内仿真模型上各个位置声压场的瞬时分布，得到接收节点的信号波形。

1.2 基于k-Wave工具箱的三维人体建模

对于超声波在体内的传输过程，仿真中需要把它离散化，采用网格方式计算。为了提高计算的精确程度，传统的差分方程和有限元法需要在一个波长范围内采用10 个以上节点，仿真复杂度和计算量很大。为了简化这个过程，可以利用采样定理，采用傅里叶级数对声压强、波速等数据进行近似拟合，以减少节点数量，通过k空间方法在降低仿真模型复杂度的同时兼顾仿真精度。k-Wave 工具箱引入了k空间方法的优化处理，建模中利用快速傅里叶变换和k 空间方法在逐点矩阵乘法的并行特点，采用多线程和图形处理器（GPU）计算进一步加快仿真速度［20］。

为了模拟体内密集多径信道，文中采用k-Wave 工具箱对人体大腿进行三维建模，用一个半径为5 cm、长为20 cm 的圆柱体表示，从内到外依次是骨骼层、肌肉层、脂肪层和皮肤层，不同组织采用不同的介质密度、声速和衰减系数进行设置，具体参数如表1所示。

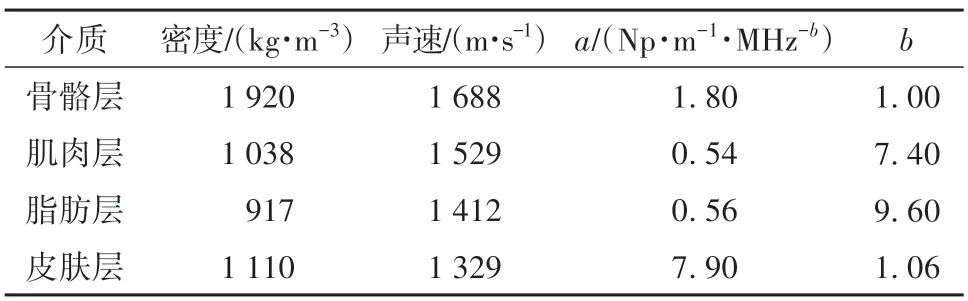
表1 k-Wave超声人体信道建模参数Table 1 Modeling parameters of k-Wave ultrasound human channels

如图1（a）所示，在肌肉层相距10 cm 的位置分别设置发射节点和接收节点，在发射节点发送狄拉克脉冲函数，这个脉冲经过人体信道传播后得到的接收信号如图1（b）所示，即信道冲激响应。

图1 基于k-Wave的超声人体信道建模Fig.1 Modeling of ultrasonic human channel based on k-Wave

可见，在超声体内通信时，超声波在体内软组织中通过不同途径传播，接收信号是密集多径的。这些多径存在正或者负的幅度，表明信号在体内传播时产生了相移，可以认为它近似是多个脉冲的叠加，图1中信道冲激响应h表示为

式中，δ是狄拉克函数，K是可以分辨的多径个数，τk、ρk和θk分别是第k条多径信号的时延、幅值衰减和相位值。

1.3 多径信道的相对时延统计特性

假定发射节点的位置固定，改变接收节点位置，保持收发节点在X轴上的投影距离为10 cm，利用信道测试的仿真实验可得到多组信道冲激响应。记录各组实验中每一条多径相对于直达径的时延，统计这个相对时延数据出现的次数和概率，可以绘制其概率密度函数，如图2实线所示。然后采用Matlab曲线拟合工具箱进行建模，得到的拟合结果用不同虚线绘制（见图2）。

图2 仿真数据的曲线拟合Fig.2 Curve fitting of simulation data

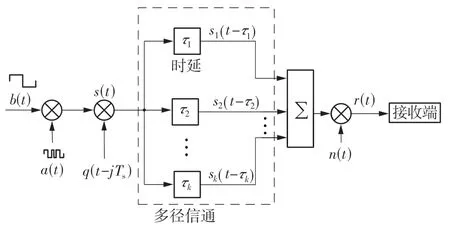
图3 DS-UsWB体内通信示意图Fig.3 Schematic diagram of DS-UsWB intrabody communication

从图2中可见，不同拟合曲线与统计结果在一定程度上具有相似性，故采用均方根（RMS）误差判断拟合效果。3 种曲线（高斯、瑞利、伽玛分布）拟合的RMS 误差分别为0.135 6、0.085 4 和0.094 0，说明大腿肌肉层超声人体信道的相对多径时延可以采用瑞利分布描述，对应的概率密度函数为

根据拟合结果可确定曲线参数σ=0.382 3。类似地，在实测实验中也可以对信道多径的相对时延进行统计和定量分析，采用曲线拟合方法获得相对时延的统计特性。

2 DS-UsWB体内通信的误码性能

根据信道建模和仿真分析可知，超声波在体内传输会产生密集多径，接收的直达信号与多路径的副本信号在接收端混叠在一起，必然对接收信号的解调造成干扰。文中对DS-UsWB体内通信进行分析，通过对多径干扰的定量计算，研究接收端误码性能的数学表述，推导出BER下界的数学表达式。

2.1 DS-UsWB体内通信的多径干扰

接收信号是由直达信号与其他路径上多个副本信号叠加形成的。假设路径k的副本信号与直达径信号存在的时延为τk，那么这个副本信号可以表示为

式中：hk=≤1，是第k条路径的增益；dk是传播距离。信号经过不同路径传播产生不同时延后，与信道中双边功率谱为N0/2的高斯噪声n(t)叠加，接收信号r(t)为

在接收端，接收信号r(t)与伪随机码a(t)进行相干解调，令Z为接收机对直达径的判决统计量，有

式中，I0是直达径对判决统计的贡献，η是热噪声部分，ζ是其他路径对直达径的干扰，

直达径信号与第k条路径信号的时序关系如图4 所示，其中τk=γkTc+Δk，0 ≤Δk≤Tc，τk是第k条路径相对于直达径信号的时延，Δk是部分码元的交叠时长。

图4 直达径信号与路径k接收信号sk(t-τk)的时序关系Fig.4 Time sequence relationship between direct path signal and the received signal sk(t-τk) from path k

可见，与多点通信干扰的推导过程类似，第k条路径信号对直达径判决形成的干扰Ik可以表示为［21］

式中，Sk=Δk/Tc，Xk、Yk、Uk、Vk分别是判决时其他路径错位码元产生的干扰，这些干扰是[0，1]上均匀分布的随机变量，详细推导见文献［21］。

2.2 DS-UsWB体内通信的BER下界

在式（7）中，将热噪声η和多径干扰ζ定义为联合干扰变量ξ，得到联合干扰变量的方差

式中，B是一个比特内PN码的边界变化。如果相邻两个码元不相同，那么B的值增加1。这说明在一个比特内，B的最大值为Ns-1，即PN 码在-1和1之间来回变换，E(B)=，将B的均值代入式（13）中，可得

利用泰勒公式展开的简化过程，E[f(x) ]的估计值可以表示为［23］

根据以上推导可知

对于高斯白噪声信道，μΨ和σ2Ψ均为0，式（18）变成

根据建模结果（式18）和E1、E2表达式可知，对于大腿肌肉层的超声建模信道，E1=-0.144 2，E2=0.292 6，代入式（19）、（22）和（18），可得到DS-UsWB体内通信的误比特率下界。推导中未考虑因多径产生的幅值衰减，将所有路径衰减视为1，实际误比特率必然高于根据式（18）的计算结果。

3 性能分析

3.1 DS-UsWB体内通信的BER

采用图1建模的多径信道进行仿真实验，假设发射节点一次发送106bit 数据，一个PN 码的码元持续时长Tc为10 µs，脉冲持续时长Ts=0.1 µs。

DS-UsWB 体内通信在高斯白噪声信道和多径信道的理论BER 下界与蒙特卡罗仿真实验的BER如图5所示。对于多径信道，理论BER下界略低于实际的仿真结果，且变化趋势一致，随着信噪比的增大这两条曲线更加接近。高斯白噪声信道下没有多径干扰，BER的理论值与仿真曲线基本重合。

图5 不同信道下DS-UsWB通信误比特率比较Fig.5 Comparison of communication BER in DS-UsWB over different channels

蒙特卡罗仿真实验结果（见图5）表明：在未扩频（Ns=1）的情况下，信噪比（SNR）为11 dB 时DSUsWB 在高斯白噪声信道的通信BER 可低至10-6，但在多径信道的通信BER 高达0.5，且随着信噪比的增加并没有明显的改善；当扩频码长Ns=5 时，高斯白噪声信道的通信BER降低明显，SNR为4 dB时BER达2×10-6，而多径信道的BER仿真值相较于未扩频时明显降低，SNR 为15 dB 时的最低BER 能达到0.001 7，但远高于高斯白噪声信道通信的最低误比特率，这说明DS-UsWB 体内通信存在明显的多径干扰，通信可靠性达不到预期效果；当Ns=10 时，DS-UsWB 通信性能在多径信道的仿真实验结果中改善明显，SNR 为14 dB 时BER 可以低至2×10-6。可见，采用扩频通信技术，接收端对多径干扰信号的频谱能量加以扩散，增大扩频码长会提高扩频增益和抗多径干扰能力，有助于提高超声体内通信的可靠性，改善程度与信噪比有关。

当信噪比为10 dB 时，多径信道仿真实验的误比特率随着扩频码长Ns的变化如图6所示，其中理论BER 下界依旧略低于仿真通信BER。从图6可知，随着扩频码长Ns的增加，误比特率逐渐降低，但Ns达到12 时，误比特率也只能达到2.4×10-4。从图5 可知，在信噪比为10 dB 的情况下，高斯白噪声信道中DS-UsWB 的扩频码长Ns只需要达到5就可以获得很低的误比特率，再次说明多径信道对通信性能造成了明显的影响。此外，虽然DSUsWB 采用的直扩技术可以降低多径干扰的负面影响，随着扩频码长的增加可以降低通信误比特率，但也会因数据冗余导致通信速率降低，实际应用中需要考虑通信性能与通信速率的折中。

图6 多径信道下通信误比特率与Ns的关系Fig.6 Relationship between communication BER and Ns over multipath channels

3.2 DS-UsWB有效通信速率

考虑多径干扰及其引起的误比特率，采用有效通信速率描述传输正确信息的能力。有效通信速率Re与误比特率RBER、通信速率Rb有关，可表示为

式中：在RBER趋于0 的情况下Re=Rb；Rp是包错误概率，可以采用上面推导的通信误比特率RBER计算；l是包长。

式（25）说明Rp受RBER的影响：RBER很高时，Rp接近为1，有效通信速率也会降低；反之，RBER很低时，Rp近似为0，有效通信速率达到最大。

固定码长Ns=10，每个脉冲的持续时间为0.2 µs，有效通信速率与信噪比之间的关系如图7所示。当信噪比达到较高值时，Rp也会随着系统误比特率的降低逐渐趋近于0。对于高斯白噪声信道，当SNR为1 dB时，误比特率已经低于10-3（见图5），因此，有效通信速率从SNR为1 dB时就达到理论上的最高值500 kb/s。在多径信道的仿真实验中，有效通信速率没有那么理想，在 SNR 为1 dB 时，多径信道的误比特率仅能达到0.13，使得有效通信速率大幅降低，但随着信噪比的提升，有效通信速率也在逐渐增加，在 SNR 为10 dB 时达到峰值，与高斯白噪声信道结果相近。可见，对于多径超声人体信道，DS-UsWB 通信需要更高的信噪比才能提高有效通信速率。

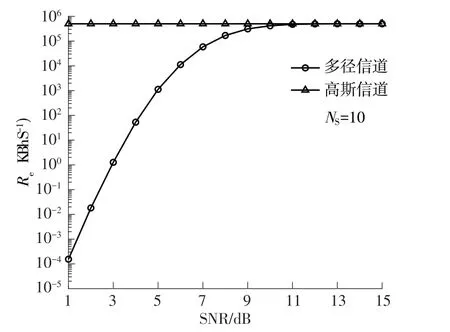
图7 有效通信速率与信噪比的关系Fig.7 Relationship between effective communication rate and SNR

4 结语

文中采用超声人体信道建模与仿真实验，对超声人体信道多径的相对时延进行了统计分析和曲线拟合，推导了DS-UsWB 超声体内通信多径干扰的统计特性及通信BER 下界，并通过蒙特卡罗仿真实验证明了理论BER 下界在多径信道和高斯白噪声信道下的有效性，表明了多径干扰在低信噪比下的影响明显，增大扩频码长可以改善通信性能。

文中的仿真工作为实际信道特性的测试提供了一种研究方案，利用多径信道的多次测试结果获得相对时延的统计特性及其统计量，可以估算通信误比特率下界，有助于通信参数的选择。此外，该方法适用于采用脉冲调制的其他通信技术，选择不同的扩频码长可以适应信道的变化。