沙漠砂混凝土框架结构的抗震性能有限元分析

张振豪,李志强*,王尧鸿,董伟

(1 石河子大学水利建筑工程学院,新疆 石河子 832003;2 内蒙古工业大学土木工程学院,内蒙古 呼和浩特 010051;3 内蒙古科技大学土木工程学院,内蒙古 包头 014010)

随着我国西部地区经济的发展,河砂需求激增,而为了避免河砂资源枯竭,许多学者开始研究应用沙漠砂资源,李志强等[1-3]探讨了沙漠砂混凝土的力学性能和柱的抗震性能,车佳玲等[4-5]通过单轴拉伸试验研究了沙漠砂制备的工程水泥基复合材料的力学性能,刘清等[6]探讨了风积砂自密实混凝土的力学性能及工作性能,董存等[7]对沙漠砂混凝土梁的受弯性能进行了试验研究,秦拥军等[8]进行了沙漠砂混凝土深梁的短期刚度试验研究,张华东等[9]对沙漠砂混凝土框架节点进行了试验研究,Liu等[10]、王尧鸿等[11]、Dong等[12]等对沙漠砂混凝土试块的耐久性能进行了相关研究。以上研究发现沙漠砂粒径较小且表面光滑,并且在混凝土中掺入适量的沙漠砂,容易形成良好的级配,改变其内部孔隙,有利于混凝土强度的形成,增加其延性和耗能[2]。由此可知通过合理配置沙漠砂混凝土可获得与普通砂混凝土相近的力学及抗震性能,并达到节约河砂的目的,但目前沙漠砂混凝土研究还局限在构件层面,以沙漠砂混凝土为框架结构主要材料的研究尚少,因此,本文利用ABAQUS有限元分析软件建立平面框架模型,研究沙漠砂混凝土框架的抗震性能,为沙漠砂混凝土框架结构的工程应用提供依据。

1 有限元模型及验证

1.1 有限元模型

参考文献[13-14]中方法采用三维实体单元(C3D8R)建立混凝土模型,采用三维线性杆单元(T3D2)建立钢筋模型,其材料力学性能指标分别见表1、表2。沙漠砂混凝土本构采用本课题组提出的应力-应变本构方程[2]。

表1 沙漠砂混凝土的材料力学性能

表2 钢筋的材料力学性能

1.2 验证模型

选用本课题组试验中的一个沙漠砂混凝土平面十字节点构件,建立有限元模型进行验证。该模型的梁截面尺寸为150 mm×250 mm,柱截面尺寸为200 mm×200 mm,上、下柱高度分别为650、700 mm,横梁长度为135 0 mm,箍筋、纵筋均选用HRB400型钢筋。横梁的配筋率为1.38%,立柱的配筋为3.02%。构件尺寸及配筋见图1,构件试验破坏形态见图2。

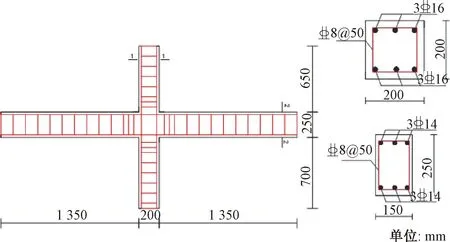
图1 尺寸及配筋图

图2 平面十字节点构件试验的破坏形态

由试验与有限元的滞回曲线(图3)可见:软件模拟获得的滞回曲线与试验滞回曲线整体吻合度较高,这说明利用该模型对框架进行模拟是可行的。

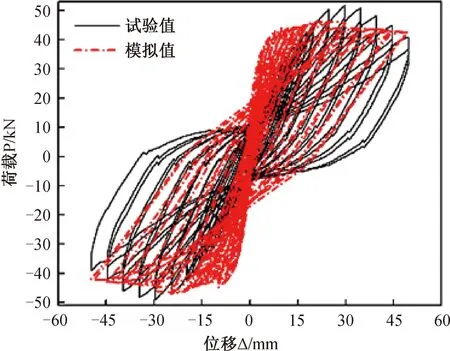
图3 荷载-位移滞回曲线试验值与模拟值对比

2 模型设计与有限元结果分析

2.1 模型设计

有限元分析模型具有可靠性和准确性,所以本研究运用ABAQUS有限元分析软件建立了9个二层平面框架模型。参考颜学渊等[13]建立的框架模型建立数值分析模型,框架层高为300 0 mm,跨度为600 0 mm,梁截面尺寸为250 mm×450 mm,柱截面尺寸为400 mm×400 mm,梁柱混凝土强度等级为C30,梁柱纵筋选择HRB400,梁柱箍筋及梁拉筋都是HPB300。图4为框架的截面图,框架设计参数见表3。

图4 框架截面图

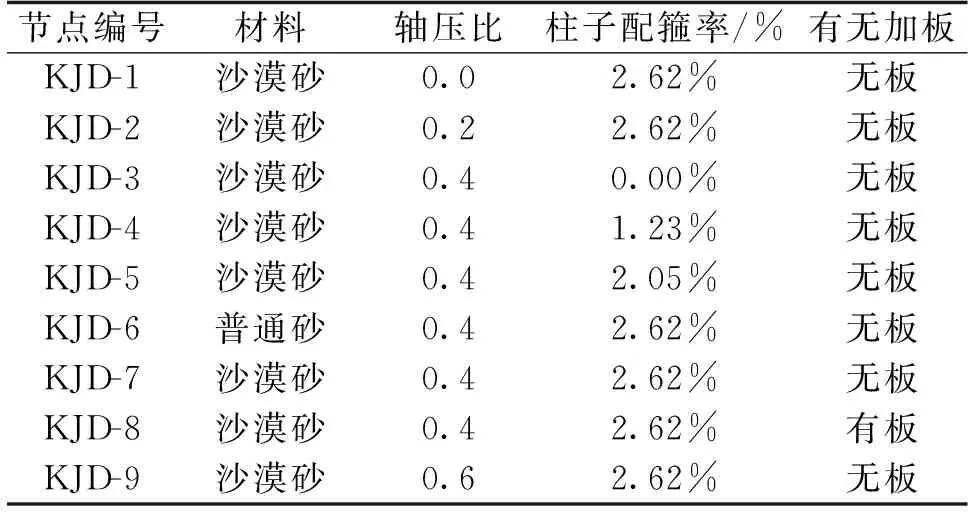
表3 沙漠砂框架设计参数

为了使框架模型在有限元运算中更易收敛[14]且减少运算时间,只在其顶层加载点处施加往复荷载。柱底边界约束X、Y和Z方向的位移和旋转,柱顶边界约束X方向的位移及Y和Z方向的旋转。混凝土框架模型按2个分析步进行加载:step1施加轴压力,此时模型不考虑几何非线性;step2施加Y方向的往复位移,考虑几何非线性。加载制度见图5,框架的边界条件见图6。

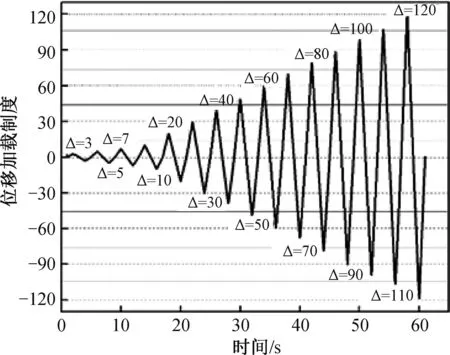
图5 加载制度图

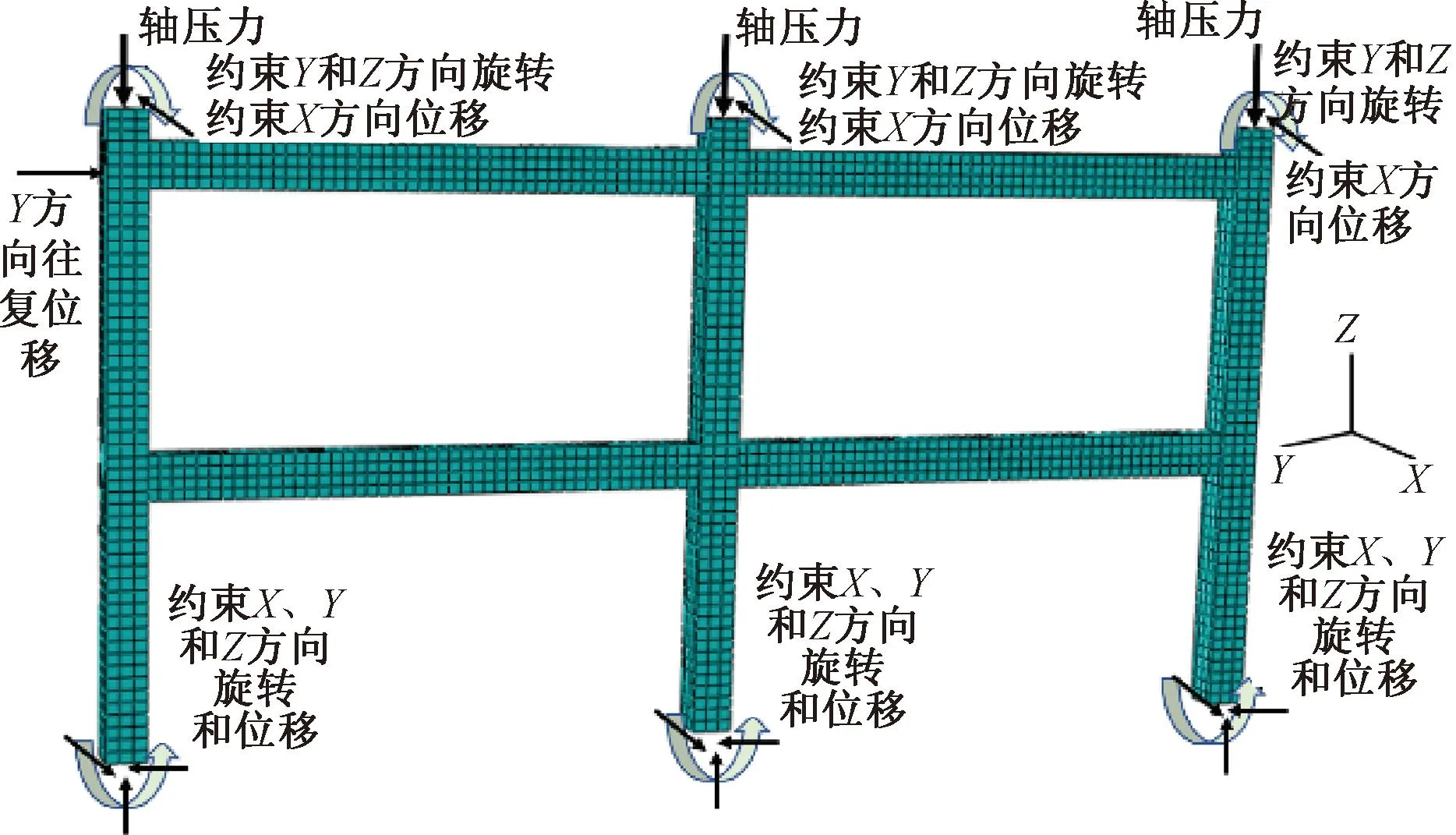
图6 空间中节点边界条件示意图

2.2 试件的破坏现象

图7为KJD-1、KJD-2、KJD-3、KJD-4、KJD-5、KJD-7、KJD-8和KJD-9在最后一个往复位移加载时的应力云图。

图7 框架应力云图

由图7可知:此位移下各节点部位及柱底发生较大塑性变形,产生了塑性铰。各节点部位及柱脚发生应力重分布,致使各节点梁端最大应力位置向梁跨中部位发生较大转移,节点部位柱子最大应力位置向柱顶方向发生较大转移。另外,各试件的破坏现象相似,破坏位置相同,其中:节点1处柱子离加载端最近,应力最大值的区域面积最小,最大应力位置向柱顶方向的转移也最小;节点3处柱子离加载端最远,应力最大值的区域面积也最大,最大应力位置向柱顶方向的转移也最大;一层4、6和8处节点的应力最大值的区域面积比二层5、7和9处节点的应力最大值的区域面积略大。

除节点2处外,KJD-8应力最大值的区域面积均比KJD-7的小(图7f、g)。这是由于加板后,楼板与梁柱浇筑在一起,整体性能提高,且板可以作为梁的翼缘,从而使梁的刚度和抗弯承载力提高。

随着轴压比逐增大,柱脚1、2和3处应力最大值的区域面积也逐渐增大且塑性铰向柱顶方向转移,柱顶5、7和9处应力最大值的区域面积也逐渐增大(图7a、b、f、h)。由图7c、d、e和f可知,随着配箍率的增大,柱脚节点1、2和3处应力最大值的区域面积逐渐减小(图7c、d、e、f)。

2.3 滞回曲线分析

由KJD-1、KJD-2、KJD-3、KJD-4、KJD-5、KJD-6、KJD-7、KJD-8和KJD-9的滞回曲线(图8)可知:在往复位移加载初期,KJD-6和KJD-7试件的滞回曲线呈线性变化,残余变形较小,但因为往复位移的增加,试件滞回曲线不断地向位移坐标轴偏移,刚度显著降低,残余变形也跟着提高(图8f、g);KJD-7和KJD-8试件的滞回曲线形状相似且呈梭形,都出现了典型的弹性阶段、弹塑性阶段和破坏阶段,但KJD-8滞回环面积显然比KJD-7大(图8g、h);随着轴压比的提高,滞回曲线包络环面积不断地提高,形状也相对饱满(图8a、b、g、i);随着配箍率的提高,滞回曲线包络环面积不断地提高,刚度退化不断地降低(图8c、d、e、g)。

2.4 骨架曲线

由骨架曲线(图9)可见:试件的承载能力增高至极限承载力后,随着轴压比的提高,试件的刚度退化不断加快(图9a),这是由框架中的柱子产生弯曲时顶部轴压力对受压区产生的附加压力增大导致的;随着配箍率的提高,试件的承载能力不断地提高(图9b);KJD-6的承载力比KJD-7略大,但刚度退化比KJD-7小(图9c);KJD-8的承载力显著大于KJD-7(图9d)。

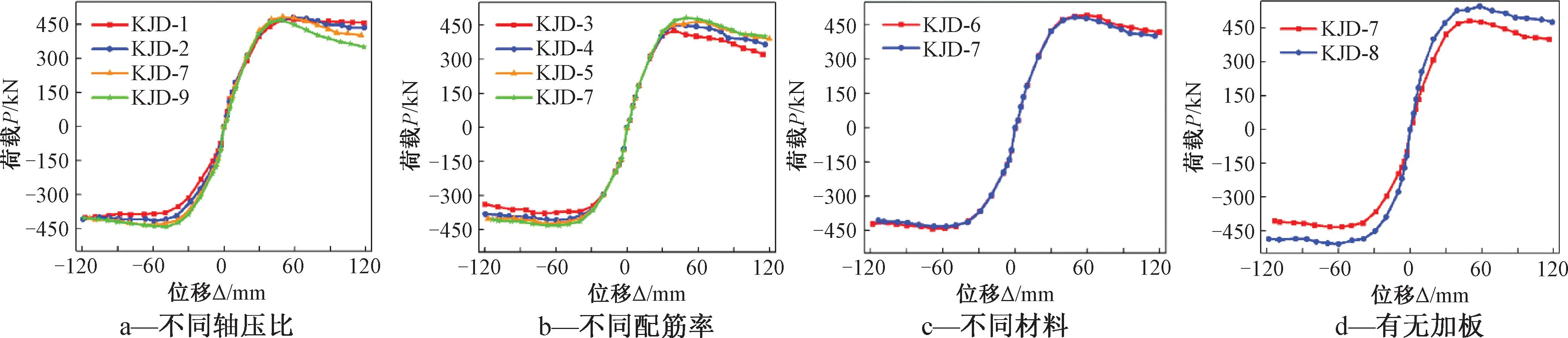
图9 构件的骨架曲线

2.5 延性系数和初始割线刚度分析

试件加载时的刚度退化用割线刚度k表示,计算公式为

(1)

式(1)中+Fy和-Fy分别是正向屈服荷载和负向屈服荷载,+uy和-uy分别是正向屈服位移和负向屈服位移。

试件屈服后的塑性变形能力用延性系数μ来表示,计算公式为

(2)

式(2)中u0.85是破坏位移,uy是屈服位移。

用几何作图法计算出每个框架的破坏位移u0.85和屈服位移uy。过O点作骨架曲线的切线交B点处的切线于点A,作A点的竖向切线交骨架曲线于E点,连接OE并延长交AB线于点D,过D点的垂线交曲线于Y点,Y点的横坐标即屈服位移uy。过极限承载力的85%作水平切线与骨架曲线相交于点C,点C对应的横坐标为破坏位移u0.85,如图10所示。

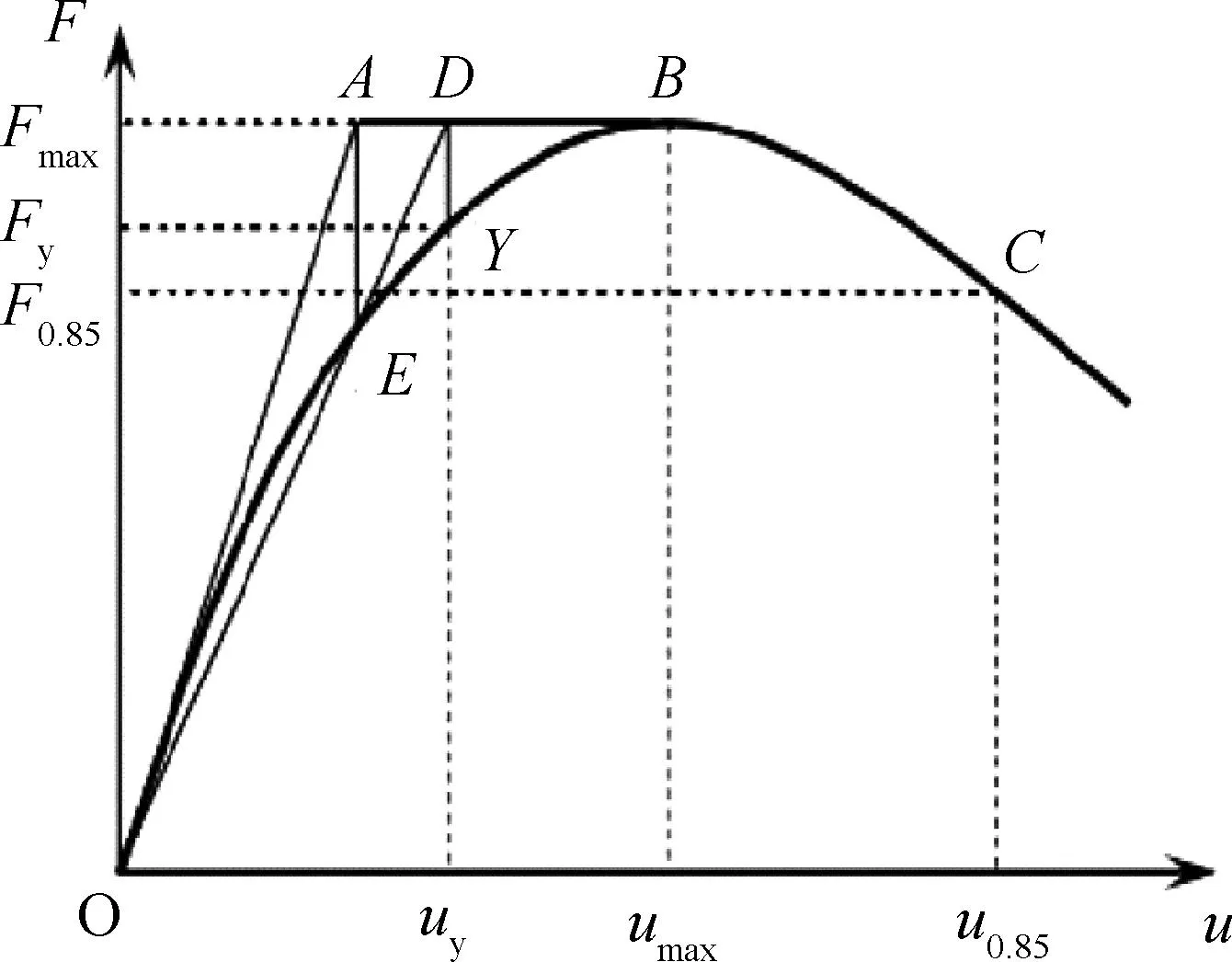
图10 几何作图法的图示说明

KJD-1、KJD-2、KJD-3、KJD-4、KJD-5、KJD-6、KJD-7、KJD-8和KJD-9的延性系数和初始刚度见表4。

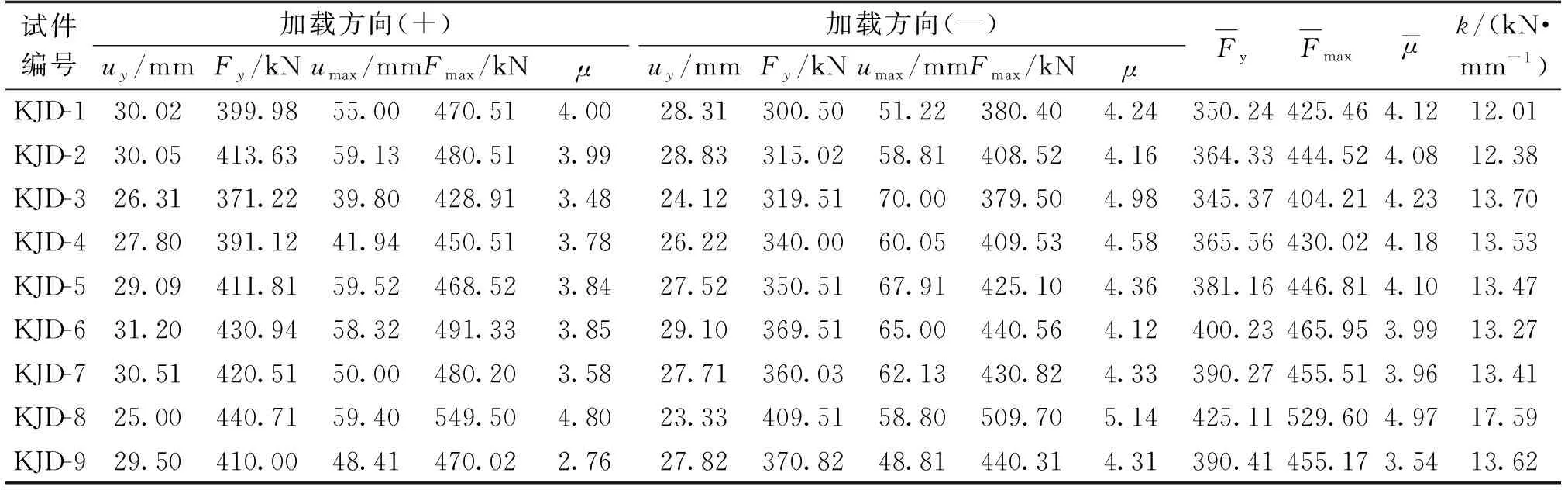
表4 延性系数和初始割线刚度

由表4可知:

(1)KJD-6的平均屈服荷载和平均极限荷载分别比KJD-7大2.49%和2.24%,平均延性系数比KJD-7大0.75%,但初始刚度比KJD-7小1.04%;KJD-6的Fmax/Fy平均值为1.17,KJD-7的Fmax/Fy平均值为1.17,说明屈服后KJD-6结构承载力余量与KJD-7相同;同时,KJD-6的umax/uy值为2.05,KJD-7的umax/uy值为1.94,说明KJD-6在屈服点至极限点变形能力储备比KJD-7高。由以上分析可知:沙漠砂混凝土的承载能力、延性略小于普通砂混凝土,结构进入屈服后承载能力余量与普通砂混凝土相同,但初始刚度相比普通砂混凝土略大,这说明沙漠砂混凝土在模拟分析中呈现出与普通砂混凝土相近的抗震性能。

(2)KJD-8的平均屈服荷载和平均极限荷载分别比KJD-7大8.20%和13.99%,平均初始刚度比和平均延性系数分别比KJD-7大20.32%和23.76%;KJD-7的Fmax/Fy平均值为1.17,KJD-8的Fmax/Fy平均值为1.25,说明屈服后KJD-8结构承载力余量比KJD-7大;同时,KJD-7的umax/uy值为1.94,KJD-8的umax/uy值为2.45,说明KJD-8在屈服点至极限点变形能力储备比KJD-7高。由以上分析可得,带板的KJD-8沙漠砂混凝土框架比不带板的KJD-7屈服荷载大8.20%,极限荷载大14%,初始刚度大20.32%,延性系数大23.76%,在屈服点至极限点承载力余量高6.40%,且变形能力储备高出20.82%。

(3)试件轴压比与平均屈服荷载和平均极限荷载都呈现正相关关系,KJD-9比KJD-1的平均屈服荷载和平均极限荷载分别大10.29%和6.53%;随着试件轴压比的增大,尽管试件的平均初始刚度随之增大,但延性系数是在减小,KJD-9平均初始刚度比KJD-1大11.82%,延性系数比KJD-1小14.08%;随着轴压比的提高,试件的Fmax/Fy平均值基本不变;除KJD-1外,随着轴压比的增加,试件的umax/uy值逐渐减小,KJD-7比KJD-2小3%,KJD-9比KJD-2小15%。由此可知,随着轴压比的增大,屈服点至极限载荷点之间的承载能力余量变化不大,但对结构变形能力储备具有较大影响,轴压比从0.2增加至0.6时,其变形能力储备减小约15%。

(4)KJD-4的平均屈服荷载和平均极限荷载分别比KJD-3大5.52%和6%,KJD-5的平均屈服荷载和平均极限荷载分别比KJD-4大4.09%和3.76%,KJD-7的平均屈服荷载和平均极限荷载分别比KJD-5大2.33%和1.91%,由此可知,每增加一个配箍率,结构的屈服载荷增长的幅度降低约1.5%,极限载荷增长的幅度降低约2%,不同的是配箍率的改变对试件的初始刚度、平均延性系数和Fmax/Fy平均值的影响较小。

2.6 耗能分析

由试件的累计耗能结果(图11)可知:KJD-6的耗能比KJD-7大1.65%(图11c),KJD-8的耗能比KJD-7大12.68%(图11d)。随着轴压比的增加,试件的耗能逐渐增大,KJD-9的耗能较KJD-1大6.36%(图11a)。KJD-4的耗能较KJD-3大7.9%,KJD-5的耗能较KJD-4大4.71%,KJD-7的耗能与KJD-5相近(图11b)。

图11 试件的累计耗能

综上可知,当轴压比小于等于0.4时,试件的耗能变化幅度较大,即每增加一个箍筋率,试件的耗能平均提高将近6.3%;当轴压比超过0.4时,试件的耗能变化幅度较小。

3 讨论

沙漠砂混凝土框架的滞回曲线及骨架曲线与普通混凝土框架相似,均呈现出弹性、弹塑和破坏阶段。与文献[15]的普通钢筋混凝土框架相比,本文所用的沙漠砂混凝土框架具有更好的延性和初始刚度,在地震作用下沙漠砂混凝土框架的变形能力较强,表现出和普通混凝土相似的抗震性能。从试件承载力及延性分析来看,与文献[16]的普通钢筋混凝土框架不同,本文所用的沙漠砂混凝土框架的承载力及延性受轴压比的影响较为显著,并且过高的轴压比会显著降低构件承载力及延性,从而导致构件发生脆性破坏。此外,沙漠砂混凝土框架增设楼板后,能够显著提高混凝土结构的整体性和抗侧力刚度,导致延性系数增加,而且随着配箍率的增加,构件的刚度退化逐渐减小,承载力逐渐增大。这些因素对沙漠砂混凝土框架性能的影响规律与普通钢筋混凝土框架的[17-18]相似,表明沙漠砂混凝土框架在建筑结构中的应用具有较好的前景,可以考虑将沙漠砂混凝土作为普通砂混凝土的替代材料。

值得注意的是,相关研究[19-20]表明混凝土配合比、钢筋布置等其他因素也对沙漠砂混凝土的抗震性能有较大影响,所以在实际应用中需要根据具体情况进行综合考虑,确保其抗震性能满足要求。

4 结论

(1)沙漠砂混凝土框架的承载能力、延性、初始刚度和屈服后承载能力余量均与普通砂混凝土框架相接近。

(2)带板沙漠砂混凝土框架的初始刚度、延性系数和变形储备能力比不带板混凝土框架高出20%左右,屈服载荷及屈服点至极限点承载力余量比不带板混凝土高出6%左右。

(3)改变轴压比,会对结构变形能力储备造成相应的影响,当轴压比由0.2升高至0.6时,其变形能力储备减小约15%。

(4)随着配箍率的增大,屈服点至极限载荷点之间的承载能力余量变化较小,且配箍率每增加一个等级,结构的屈服载荷增长的幅度降低约1.5%,极限载荷增长的幅度降低约2%。

(5)沙漠砂混凝土框架在往复力作用下最易破坏的位置位于柱脚和梁柱交接处,且随着位移的增加,柱底最大应力转至柱顶,梁端最大应力转至跨中。