方形转动摩擦阻尼器工作原理及滞回性能研究

闫丽娟,张春巍

(1. 青岛理工大学 土木工程学院,山东 青岛 266033; 2. 青岛城市学院 土木工程学院, 山东 青岛 266100)

0 引言

建筑结构振动控制的概念是在20世纪70年代被提出的,最初KELLY等提出在结构中设置非结构构件的装置来分担构件应该耗散的能量的设想。之后,各国学者纷纷研究出各种形式的耗能装置。阻尼器作为耗能装置之一,分为速度相关型和位移相关型[1-2]。速度相关型阻尼器指黏滞阻尼器和黏弹性阻尼器。

摩擦阻尼器是在20世纪70年代末开始发展起来的,它的工作原理是利用元件之间相互滑动产生的摩擦力做功消耗能量,从而减小结构在地震作用下的反应。PALL等[3-4]阻尼器问世,它是在框架支撑的相交位置处放入摩擦垫板,在地震作用下,相交处会出现滑动,利用滑动摩擦做功来消耗地震能量。FILIATRAULT等[5]进行了首个摩擦阻尼器钢框架结构的振动台试验,对比不同形式的结构模型的抗震性能,结果表明安装Pall阻尼器的钢框架结果耗能能力良好。日本Sumitomo公司在高层建筑中使用Sumitomo 摩擦阻尼器[6],该阻尼器是利用活塞杆在圆柱形钢筒内滑动时,摩擦垫块滑动进行消耗能量。NIM等[7]对向心式摩擦阻尼器的双旗帜形滞回模型、三角形滞回模型等力学模型进行了理论分析。ONO等[8]研究了影响摩擦阻尼器性能的因素:压强、摩擦材料、摩擦板厚度、加载制度等。MUALLA等[9]提出了新型转动摩擦阻尼器,进行了转动摩擦阻尼器滞回性能的试验研究,并对安装有转动摩擦阻尼器的钢框架进行了试验和数值模拟研究。吴斌等[10-11]在Pall型摩擦阻尼器的基础上,提出了T形芯板摩擦阻尼器,并对T形芯板摩擦阻尼器进行了摩擦系数试验、滞回性能试验及其数值模拟分析。MONIR等[12]在 Pall型阻尼器的基础上,设计了“田”字型转动摩擦阻尼器,对该阻尼器进行了滞回性能试验分析,并对安装该阻尼器的单层钢框架结构进行了振动台试验分析和数值模拟分析,表明该转动摩擦阻尼器有较好的耗能能力。SANATI等[13]在Mualla研发的转动摩擦阻尼器的基础上添加了一些黏弹性垫片和摩擦盘,提出了一种新型转动摩擦黏弹性阻尼器(RFVD),这种阻尼器可以在低激励下实现较大的耗能。SAMANI等[14]设计了可变摩擦力的摩擦阻尼器,对其进行试验及有限元模拟分析。张艳霞等[15]通过对 5 个长孔螺栓摩擦阻尼器的试验研究,分析阻尼器的摩擦力、滞回性能及耗能能力。隋伟宁等[16]设计了一种可用于多种结构的转动摩擦阻尼器,通过试验研究和有限元软件模拟分析了摩擦系数、摩擦面个数及螺栓预紧力对阻尼器性能的影响,提出了转动弯矩M与施加荷载F之间的关系式。杨小琦等[17]提出了一种L形转动摩擦阻尼器,并进行了阻尼器的滞回性能试验分析和有限元模拟。

目前,很多国内外学者对转动摩擦阻尼器进行了研究,并有一些应用实例。本文提出了一种正方形转动摩擦阻尼器,并对阻尼器的工作原理和滞回性能进行了理论分析及数值模拟。

1 方形转动摩擦阻尼器构造

提出的方形转动摩擦阻尼器可以作为耗能装置应用于带斜撑钢框架结构中形成消能减震钢框架,具体装置示意如图1所示。该阻尼器设置于斜撑中,不仅可以通过转动摩擦消耗能量,还可以弥补受压斜撑容易压屈的缺点,提高整体结构的抗震性能,此外,方形转动摩擦阻尼器连接件之间的初始角度均为90°,初始形状为正方形,相对其他角度与形状更易于加工连接,且阻尼器构造简单,便于安装,具有较好的应用前景。

图1 消能减震钢框架示意图Fig. 1 Schematic diagram of energy dissipation and shock absorption steel frame

方形转动摩擦阻尼器主要由连接件、摩擦片、垫片、普通螺栓和高强螺栓五部分组成,如图2所示。阻尼器耗能端的每个摩擦片均由2个连接件固定并采用高强螺栓进行预压紧固;为了利于阻尼器的连接件在外力作用下发生相对转动,加载端采用普通垫片替代摩擦片,并用普通螺栓将其紧固,为了更准确研究摩擦片的耗能能力,可将加载端的垫片涂润滑剂处理。阻尼器具体构造如图3所示。

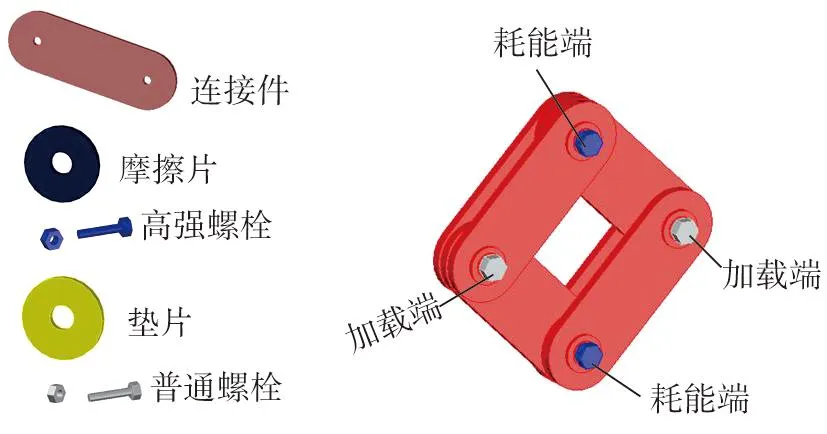
图2 阻尼器3D大样Fig. 2 3D detail of damper

图3 阻尼器构造组成Fig. 3 Structural composition of damper

2 工作原理

方形转动摩擦阻尼器的力学模型如图4所示。理论分析时,假定该阻尼器仅在安装摩擦片的耗能端进行转动摩擦耗能,加载端的普通垫片和普通螺栓只起连接及滑动作用,不进行摩擦耗能。

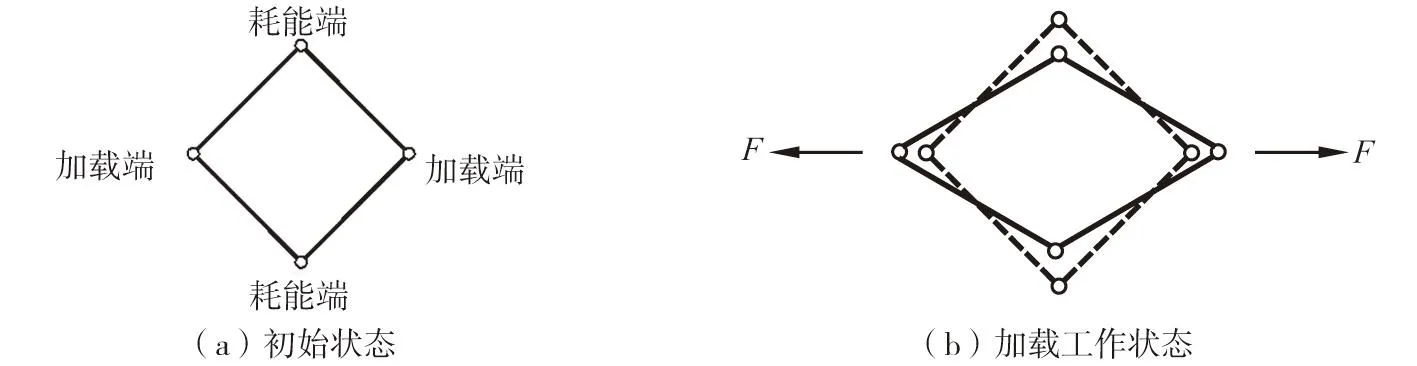
图4 阻尼器力学模型Fig. 4 Mechanical model of damper

结构上下对称,取图4(b)中上半部分进行分析,并将其耗能端端点统一到A点,如图5所示。阻尼器连接件AB(AC)长度为L,两连接件之间的初始夹角为2θ(θ=45°),在F作用下连接件绕着A点转动,B(C)点移动到了B＇(C＇)点,假定此时连接件与竖直轴线夹角为φ,加载端至阻尼器几何中心的距离为x,则x=Lsinφ。在φ的基础上产生虚位移δφ,则δx=δφ·Lcosφ,根据虚功原理可得:

2Fδx=nM·2δφ

(1)

将δx=δφ·Lcosφ代入式(1),得:

(2)

式中:F为阻尼器端部所受外荷载;M为阻尼器单个摩擦片的转动摩擦力矩;n为摩擦片个数;L为阻尼器连接件中心距离。

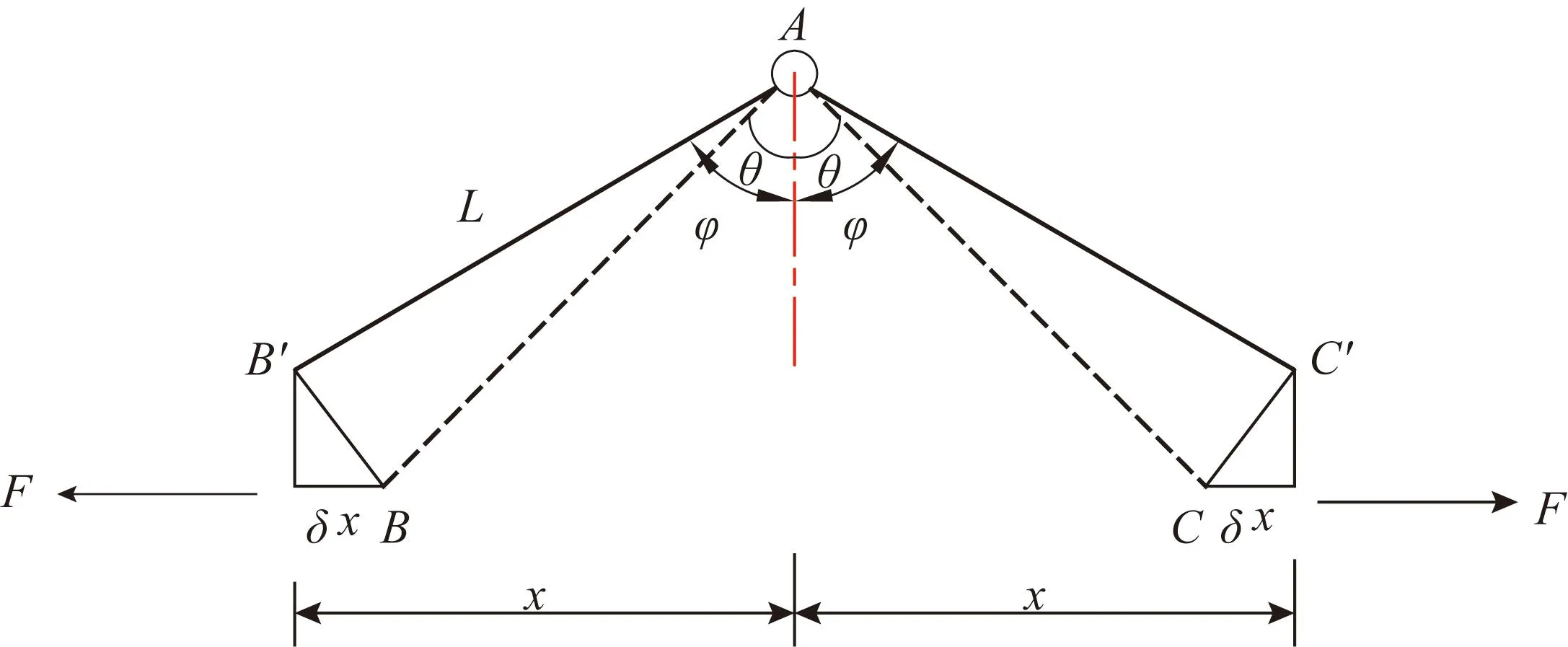
图5 隔离体受力图(正向加载)Fig. 5 Stress diagram of isolator (positive loading

(3)

摩擦片工作原理如图6所示,当连接件转动dφ时,摩擦片转动角度也是dφ,取摩擦片微元体dA,则微元体的摩擦力为:

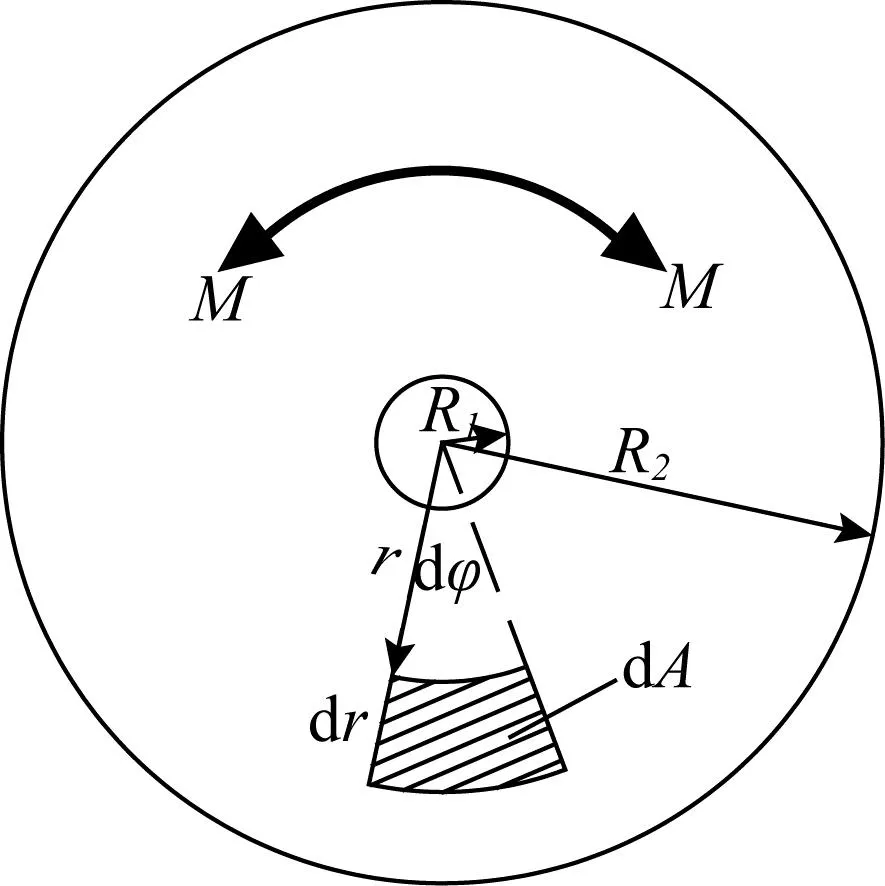
图6 摩擦片工作原理Fig. 6 Working principle of friction plate

df=μpcdA

(4)

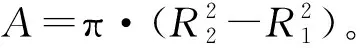
微元体摩擦力df对摩擦片中心取矩,可以得到:

dM=df·r=μpcr2dφdr

(5)

对式(5)积分可得摩睛转动摩擦力矩为:

M=∬μpcr2dφdr

(6)

对整个摩擦片求定积分,可得阻尼器中单个摩擦片的转动摩擦力矩为:

(7)

式中R1、R2分别为摩擦片开孔半径和摩擦片半径。

3 滞回性能理论分析

3.1 F-Δ关系推导

根据对阻尼器工作原理的分析,结合式(2)、式(3),可以得到施加正向荷载时滑移力F与水平位移Δ的关系为:

(8)

因阻尼器中摩擦片始终处于压紧状态,所以无论阻尼器转动角度多大,单个摩擦片的转动摩擦力矩均为定值M,将式(7)代入式(8)可得正向加载时阻尼器的F-Δ关系式为:

(9)

施加反向荷载时阻尼器的受力分析如图7所示,用与正向加载同样的方法可以求得对阻尼器反向加载时的F-Δ关系为:

图7 隔离体受力图(反向加载)Fig. 7 Stress diagram of isolator (negative loading)

(10)

3.2 算例分析

阻尼器连接件长L=160mm,宽80mm,厚度10mm,摩擦片和垫片直径均为80mm,厚度4mm,高强螺栓和普通螺栓均为M12,具体构造如图8所示。

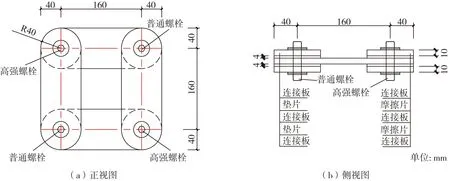
图8 阻尼器构造尺寸Fig. 8 Structural dimensions of damper

根据JGJ/T 101—2015《建筑抗震试验规程》[18]规定,对该阻尼器采用位移控制加载,最大位移20mm,加载时间25s。摩擦片数量n=4,摩擦系数取0.6,根据相关规范对高强螺栓施加预紧力P=50kN,摩擦片螺栓孔半径R1=7mm,摩擦片半径R2=40mm。

根据式(9)和式(10),可以得到阻尼器所施加的荷载F与其产生的位移之间的关系曲线,如图9所示。由图9可知,阻尼器具有较大的初始刚度,滞回曲线基本呈矩形,表明方形转动摩擦阻尼器具有较好的耗能能力。正向加载时,阻尼器滑移力随着位移的增大而增大,反向加载时则相反,其原因主要是摩擦片与连接件表面始终处于压紧接触状态,因此产生的摩擦力矩与两者的相对转动角度无关,即M为定值;加载端施加的力F与力臂Lcosφ形成力偶抵抗摩擦力矩M,正向加载时,力臂逐渐减小,所以F逐渐增大,反向加载时,力臂逐渐增大,所以F会减小。

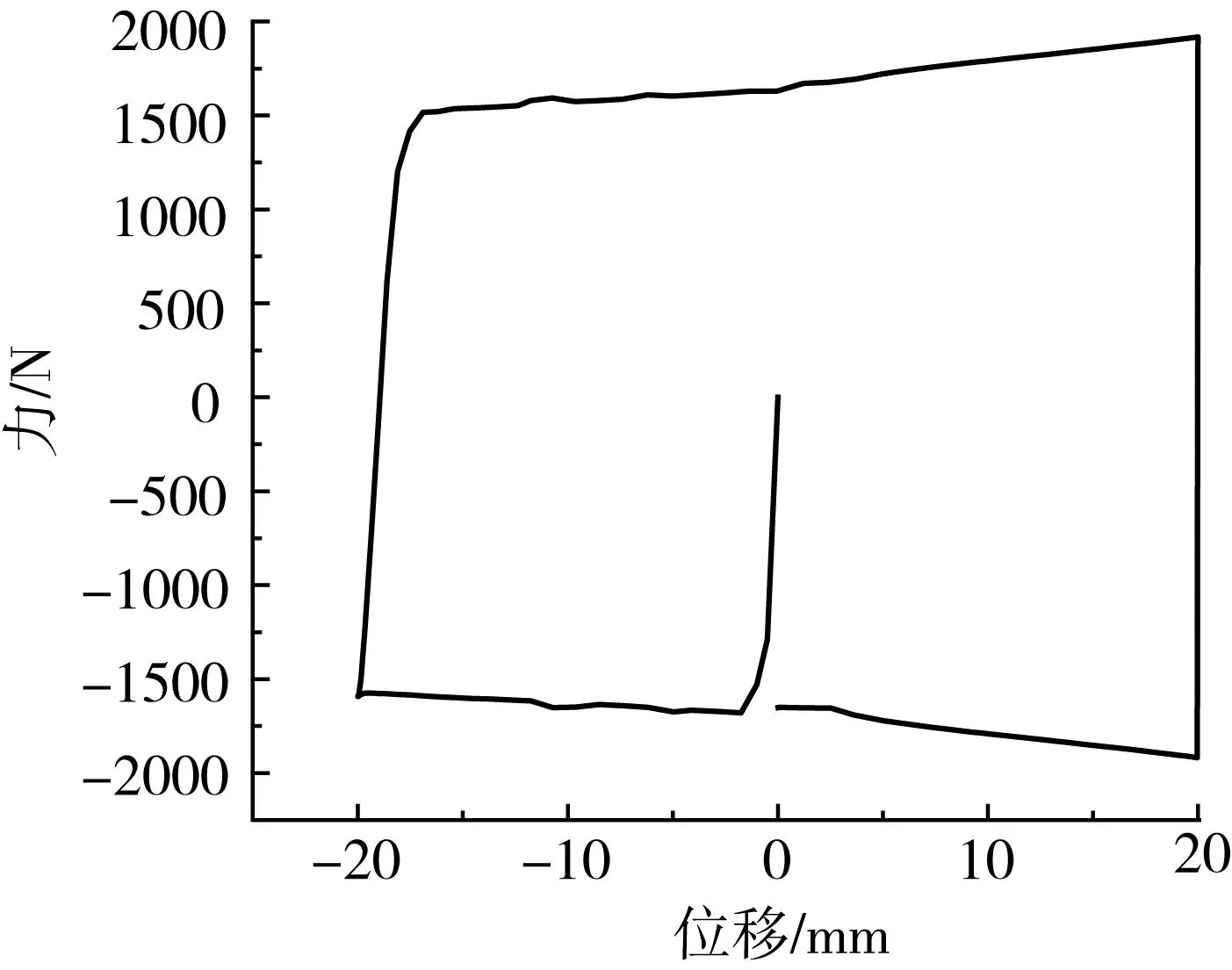
图9 力-位移关系曲线Fig. 9 Force-displacement relation curve

4 方形转动摩擦阻尼器有限元模拟分析

为了对理论算法的结果进行验证,运用有限元软件ABAQUS对上述算例中的方形转动摩擦阻尼器进行模拟分析。

4.1 有限元模型建立

有限元建模包括阻尼器各部件的几何设置、材料属性设置、装配以及单元类型的选取和网格划分、定义约束、定义相互作用关系、定义边界条件和荷载施加方式等方面。

为确保有限元模拟的精确性,转动型摩擦阻尼器中各部件均采用三维实体单元(C3D8) ,采用结构优化网络技术对模型进行网格划分,有限元模型如图10所示。

图10 方形转动摩擦阻尼器有限元模型Fig. 10 Finite element model of square rotating friction damper

4.2 模型连接单元设置

方形转动摩擦阻尼器为机构体系,阻尼器中的连接件、摩擦片和垫片通过高强螺栓或普通螺栓进行相互连接,各部件之间存在着相互约束关系和相对运动关系,属于多体运动。需要通过设置连接单元来模拟各部件之间的相对运动。其中,连接件采用平移连接单元AXIAL以模拟其在轴向不发生变形的要求;高强螺栓和摩擦片、普通螺栓和垫片之间的运动通过设置组合连接单元HINGE进行模拟。该有限元模型共有6个AXIAL单元,20个HINGE单元。

4.3 模型各部件接触及边界条件设置

方形转动摩擦阻尼器中各部件的接触有连接件与摩擦片、连接件与垫片、高强螺栓与连接件、高强螺栓与摩擦片、普通螺栓与连接件、普通螺栓与垫片等。为了方便准确模拟阻尼器的工作,有限元模型中将连接件与摩擦片的接触定义为表面与表明接触,其余均定义为通用接触。接触属性按照库伦摩擦原理,设置切向行为与法向行为,切向行为取库伦摩擦系数,法向行为定义为“硬”接触。理论算法假定只有高强螺栓预紧后的摩擦片转动摩擦耗能,普通螺栓连接的垫片不参与耗能,所以摩擦片与连接件接触的摩擦系数取值与算例相同,垫片与连接件接触按无摩擦考虑。

为了模拟阻尼器两端加载的情况,将普通螺栓的边界条件设置为U2=U3=0,R1=R2=R3=0;并在普通螺栓螺杆中心定义参考点,对该参考点进行位移加载。高强螺栓的预紧力则通过对摩擦片表面施加预压力来实现。

4.4 模型加载制度

在参考点RP1和RP2施加位移荷载,具体加载制度同3.2节算例。加载模型如图11所示。

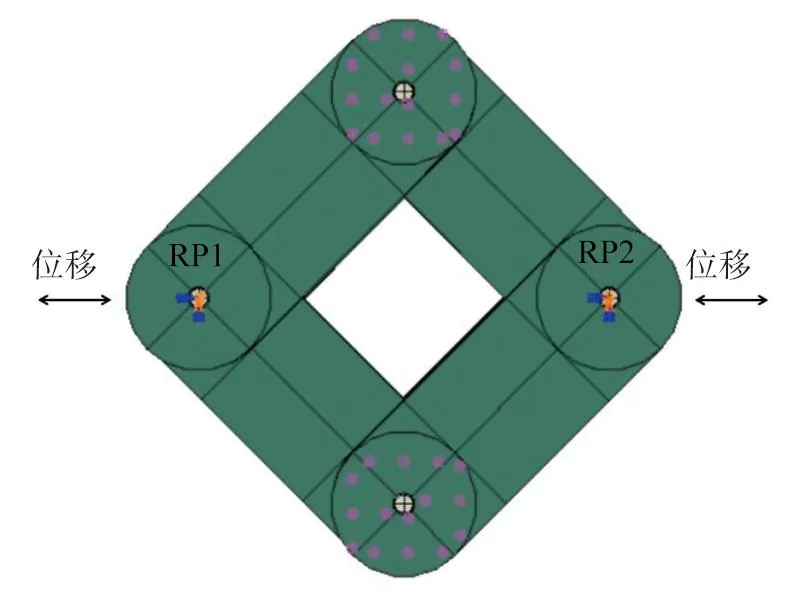
图11 方形转动摩擦阻尼器加载模型Fig. 11 Loading model of square rotating friction damper

4.5 模型有限元分析与理论分析结果对比

方形转动摩擦阻尼器算例有限元分析得到的滞回曲线,如图12所示。由图可知,有限元分析结果与理论分析得到的滞回曲线形状一致,且正反向加载时的变化规律也是基本相同;对比分析可以得到:有限元模拟与理论计算得到曲线基本吻合,可以初步确定该理论计算公式基本正确,后期可以通过试验加以验证。此外,图中曲线都比较饱满,可以较好地反映方形转动摩擦阻尼器的工作性能,说明阻尼器有较强的耗能能力。

图12 滞回曲线对比Fig. 12 Comparison of hysteretic curves

5 结论

通过对方形转动摩擦阻尼器滞回性能的理论分析和有限元软件模拟分析,可以得出以下结论:

1)方形转动摩擦阻尼器的理论分析与有限元模拟分析得到的滞回曲线基本吻合,验证了该理论公式的合理性。

2)方形转动摩擦阻尼器在正向加载和反向加载时,其滞回曲线表现出相反的变化规律。正向加载时,阻尼器反力随位移的增加而增大,反之则减小。

3)理论分析与有限元模拟分析得到的滞回曲线均比较饱满,说明该方形转动摩擦阻尼器具有较好的耗能能力。

4)在地震作用下,摩擦面的摩擦力可能会受到荷载速率、温度等条件的影响,可进一步开展具体的试验研究。