超高强钢筋UHPC梁受弯性能试验研究及承载力分析

张健新,赵晓雪,戎 贤,翟越洋,原伟涛

(1. 河北工业大学 土木与交通学院,天津 300401; 2. 河北省土木技术创新中心,天津 300401)

0 引言

超高性能混凝土是一种强度高、韧性好和耐久性高的新型水泥基复合材料,其抗压强度为120～180 MPa。由于UHPC优异的力学性能,在结构中使用其替代普通混凝土时,大约可减少1/3～2/3的混凝土用量[1],降低运输成本。由于其优异的耐久性,UHPC可具备较长的使用期限,有效减少结构维修费用。此外,UHPC能够减小环境污染和能源消耗,符合国家绿色低碳的政策导向,具有良好的社会效益和经济意义。另一方面,UHPC具有更大的抗拉强度,可以较好地控制荷载下的开裂和变形,这在减少钢筋用量时尤为重要。BARBACHYN等[2]对钢筋总重量和施工成本进行了参数数值研究,并揭示了钢筋混凝土墙中使用高强钢筋和高强度混凝土的经济效益。

因此,国内外学者对超高性能混凝土梁受弯性能开展了系列研究工作[3-6]。为研究不同配筋率下UHPC梁的开裂行为和应力响应,HASGUL等[7]和YOO等[8]评估了UHPC梁的受弯性能,研究了UHPC混凝土的开裂后刚度和承载力随配筋率的变化情况。梁兴文等[5]分析钢纤维体积掺量对UHPC梁受弯性能的影响,YOO等[9]对UHPC梁中掺加的钢纤维类型进行承载力评估,这些UHPC梁受弯试验表明其具有良好的受弯性能。郑文忠等[10]研究了6根钢筋超高性能混凝土梁的变形和裂缝分布,表明在梁的受弯设计中应考虑UHPC在受拉区的拉应力。彭飞等[11]提出一种钢筋UHPC梁受弯承载力的简化计算方法。上述UHPC梁受弯性能研究中纵向受拉钢筋屈服强度小于或等于500 MPa,未见梁中采用更高强度受拉钢筋。因此UHPC与更高强度钢筋结合的有效性需进一步研究。

为减少梁钢筋用量,许多学者开展了高强钢筋混凝土梁受弯性能研究[12-16],管俊峰等[17]进行了高强钢筋混凝土梁在集中荷载作用下的受弯性能试验。为提高梁的抗裂能力,廖桥等[18]针对超高强钢筋(屈服强度标准值≥500 MPa)工程用水泥基复合材料(engineered cementitious composites, ECC)梁进行了受弯性能试验研究,李碧雄等[19]建立了屈服强度标准值大于等于500 MPa的超高强钢筋ECC梁的受弯计算理论。与普通钢筋混凝土梁相比,配置高强钢筋的梁配筋率能够得到降低,在实际工程中创造了良好的经济效益,ECC优异的控裂能力能够显著提高梁的抗裂性能和延性性能。上述研究表明,高强钢筋的使用对于减少钢筋用量具有积极作用,高强钢筋混凝土梁具有较高的抗拉强度和较大的弹性范围,因此具有更好的抗弯能力。

但是高强钢筋的高屈服应变使梁易发生脆性破坏,而且高强钢筋与普通混凝土配合使用时,裂缝宽度往往超过规范限值,并降低梁刚度,其高强度难以充分利用。UHPC是一种潜在的解决方案,可控制裂缝发展,延缓压碎破坏。630 MPa钢筋是一种新型热处理带肋钢筋,UHPC和630 MPa钢筋协作可以实现潜在的材料性能,具有高强度、高耐久性和许多其他优势。目前尚无此种超高强钢筋UHPC梁受弯性能相关研究,因此有必要开展该构件的受弯试验研究,并了解不同配筋率的630 MPa钢筋混凝土梁受弯性能的差别。同时提出了相应的受弯承载力计算方法,根据国内外43根试验梁,验证提出的承载力计算公式的适用性。

1 试验概况

试验共设计4根超高强钢筋UHPC/NC简支梁,包括2根受拉钢筋配筋率1.59%和1.88%的UHPC梁,2根受拉钢筋配筋率1.59%和1.88%的NC对比梁。试验梁长2.1 m,计算跨度1.8 m,矩形截面尺寸为150 mm× 250 mm。梁底部纵向钢筋采用屈服强度标准值630 MPa的新型钢筋,架立筋和箍筋选用HRB400钢筋。为了避免剪力对梁的受弯性能产生影响,在梁中部600 mm纯弯曲段内不设置箍筋。同时为了防止将架立筋当作受压钢筋而对正截面承载力计算产生影响,纯弯曲段不设架立筋。试验梁的几何尺寸和钢筋布置如图1所示,试件设计参数如表1所示。

图1 钢筋详图Fig. 1 Reinforcement details

表1 试件设计参数Table 1 Design parameters of specimens

试验中使用的UHPC由水泥、硅灰、石英砂、石英粉、高效减水剂、水和钢纤维组成,其配合比如表2所示。钢纤维直径为0.21 mm,长13 mm,抗拉强度为2950 MPa。UHPC的制备过程如下:先在搅拌机中放入硅粉、石英砂、石英粉和水泥搅拌3 min;然后按比例混合水和高效减水剂,分2次倒入混合物中,每次搅拌3 min;最后,边搅拌边倒入钢纤维,持续搅拌8 min,使材料分散均匀。

表2 UHPC配合比Table 2 UHPC mixture proportion kg/m3

制备了9个100 mm ×100 mm × 100 mm的立方体试块,测量得到UHPC和NC的立方体抗压强度标准值为115.2 MPa和39.6 MPa,钢筋强度实测平均值如表3所示。

表3 钢筋力学性能实测值Table 3 Measured value of mechanical properties of reinforcement

使用50 t电液伺服压力试验机对试验梁进行两点弯曲加载,通过分配梁对试件施加间距为600mm的两点集中荷载,加载装置如图2所示。为了测量梁的跨中挠度,在2个支座顶部、加载点底部和跨中设置5个位移传感器,在梁跨中正反面分别布置混凝土应变片和应变测点,梁底跨中纵筋粘贴钢筋应变片。试验中用精度为0.01mm的手持式显微镜测量裂缝宽度,试件的荷载、位移和应变通过数据采集系统得到。

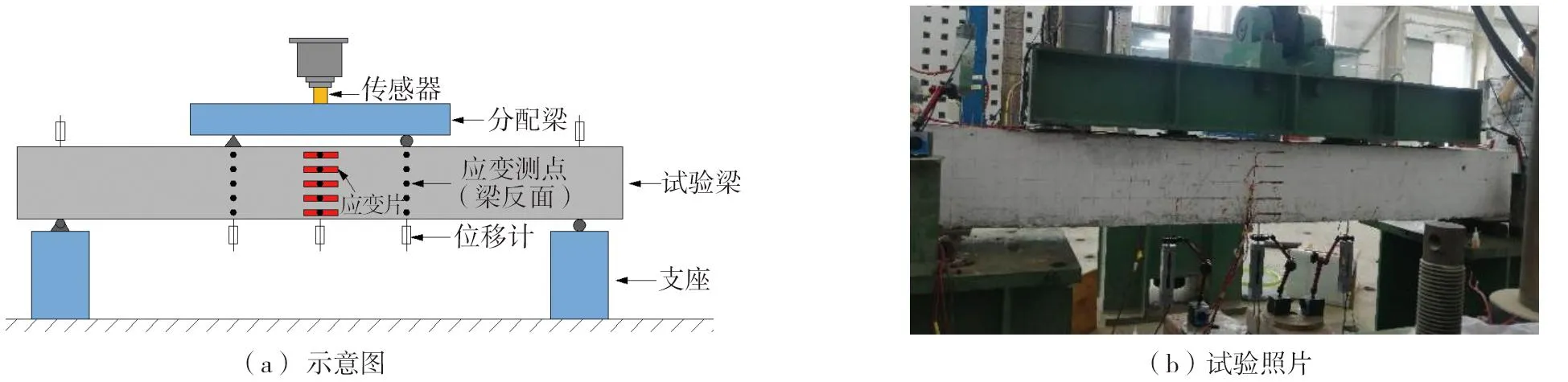
图2 试验装置及测点布置Fig. 2 Test setup and measuring-point arrangement

在试验开始前进行预加载,以检查支架、测量仪器和加载设备,预加载值不得大于极限荷载的0.05倍,且应小于开裂荷载。试验加载制度采用分级加载,在加载到90%的开裂荷载之前,每级加载约为0.2倍的开裂荷载,直到荷载达到开裂荷载的90%后,每级加载变为0.05倍的开裂荷载;试件开裂后,每级荷载控制在极限荷载的0.1倍,当荷载达到0.9倍的极限荷载后,每级加荷为0.05倍的极限荷载,直到试件破坏。在每个加载阶段,宜持荷载5min ,以便裂纹充分发展并便于记录。

2 试验现象

2.1 破坏形态

4个试验梁的破坏模式均为延性良好的受弯破坏,所有梁的主裂缝均位于纯弯区段。UHPC梁和NC梁的破坏模式明显不同,超高强钢筋NC梁纵向受拉钢筋屈服后,顶部受压区混凝土大量压碎,出现明显的弯曲变形,而超高强钢筋UHPC梁的纵向受拉钢筋屈服,底部出现较宽主裂缝,受压区混凝土未发生明显破坏,且未出现明显变形。基于梁的破坏形态分析可以发现,630 MPa超高强钢筋UHPC梁承载能力更强,安全储备更多,对梁的变形产生了较好的约束作用。

2.2 裂缝发展与分布

虽然4根试验梁的破坏形态不相同,但梁的加载过程都经历了3个阶段:第一阶段为线弹性阶段,梁上无裂纹产生;第二阶段梁中开始出现裂缝并向上延伸,梁底部受拉钢筋屈服;第三阶段是屈服后的大变形阶段,在此阶段,梁荷载基本保持不变,而挠度快速增加,试验梁的裂缝分布和荷载-裂缝宽度曲线分别如图3和图4所示。

图3 梁裂缝分布Fig. 3 Crack distribution of beam

图4 荷载-最大裂缝宽度曲线Fig. 4 Load-maximum crack width curves

加载到开裂荷载时,首先在梁的纯弯曲区域沿梁底面出现细小的竖向裂缝,裂缝宽度不大于0.02 mm。随着荷载增加,裂缝数量增多,开始出现在纯弯曲区域以外,并逐渐向上开展延伸。达到试件的屈服荷载时,裂缝数量基本保持不变,裂缝宽度迅速增大。与此同时,可听到钢纤维被拔出、拉断的声音。由图3(c)、(d)中可知,超高强钢筋NC梁纯弯区段出现了由加载点向下延伸的斜裂缝,这是由于加载至极限荷载时,加载点附近混凝土在集中荷载作用下出现压应力集中,使得此区段产生较大剪力,而未配置抗剪箍筋,所以出现斜裂缝,混凝土被压溃。

对比UHPC和NC试验梁,由图3可以明显看出超高强钢筋UHPC梁BU1和BU2的裂缝形式为数量多且宽度小的多缝开裂模式,裂缝条数分别为31和30,梁受压区混凝土仅表面轻微脱落,整个梁基本保持完整,而BN1和BN2裂缝条数分别为15和16,裂缝宽度和间距均较大。由图4可知,各试件在受拉钢筋屈服前,最大裂缝宽度随荷载近似线性增长,钢筋屈服后,最大裂缝宽度迅速增加。UHPC梁开裂荷载明显高于NC梁,并且裂缝宽度发展较慢。在相同荷载条件下,UHPC梁最大裂缝宽度明显小于NC梁。表明UHPC梁中大量乱向分布的钢纤维能有效延缓裂缝开展,同时UHPC与超高强钢筋能很好的工作,显著提高梁的承载能力。

由图3和图4中纵筋配筋率不同的3组试件,可以发现裂缝宽度和数量受纵向钢筋配筋率的影响较小,但对裂缝开展长度影响较大。由各试件的裂缝开展情况可以看出,纵筋配筋率较低的试件裂缝长度较长,配筋率较高的试件裂缝较短。这是由于较高纵筋配筋率的梁提供了较大的拉力,为了保证试件截面拉压平衡,因此需要较高的受压区高度提供压力以平衡纵向受拉钢筋的拉力。

3 试验结果分析

3.1 荷载-挠度曲线

4根试验梁的跨中荷载-挠度曲线如图5所示,各试验梁的开裂、屈服和极限荷载及屈服位移和极限位移如表4所示。所有试件的曲线形状基本相同,均包含3个点,即开裂点、屈服点和峰值点。开裂点为试验梁跨中出现第一条竖向裂缝对应的荷载。根据参考文献[20]的方法确定屈服点,即最远点法。通过连接原点和峰值点,确定距离其连接线最远点为屈服点。峰值点为受压区混凝土压碎对应的荷载。

图5 梁的荷载-挠度曲线Fig. 5 Load-deflection curves of beams

表4 梁的特征荷载Table 4 Characteristic load of beam

由试验现象和图5可以看出试验梁有如下特点:

1)在初始加载阶段,荷载-挠度曲线成线性,梁上无裂缝产生, 结构处于弹性阶段。随着荷载的增加,梁侧面出现裂缝, 曲线的斜率首次变小, 由于UHPC的阻裂作用,BU1和BU2的斜率减小并不明显。随着荷载继续增加,裂缝宽度增大、数量增多,直到受拉钢筋屈服,裂缝数量基本保持不变,而宽度迅速增大,曲线的斜率出现第二次变小。继续加载,NC梁受压区混凝土压碎,此时荷载值几乎没有变化,但挠度迅速增加;而UHPC梁的荷载-挠度曲线呈现缓慢的上升趋势。

2)随着配筋率由1.59%增加到1.88%,UHPC梁和NC梁的屈服荷载增加了27.8%和18.7%,极限荷载提高了17.4%和13.3%。增加梁纵筋配筋率能够提高梁的屈服荷载和极限荷载,值得一提的是,同样配筋率从1.59%到1.88%,超高强钢筋UHPC梁的屈服荷载和极限荷载比超高强钢筋NC梁提高幅度更大,这表明630 MPa的超高强钢筋与UHPC梁结合后效率更高。这是由于UHPC的高粘结提高了钢筋与混凝土之间的粘结强度,从而提高了构件承载能力。

3)以受拉钢筋配筋率为1.88%为例,本文中超高强钢筋UHPC梁比超高强钢筋普通混凝土梁承载力提高36.3%。而相关文献[21]中,当钢筋强度等级为400 MPa时,将配筋率的影响进行归一化处理,UHPC梁比C30混凝土梁和C50混凝土梁的承载力分别提高16.9%和13.5%。应用超高强钢筋的混凝土梁承载力提高幅度远远大于低强度钢筋混凝土梁,这表明超高强钢筋与UHPC结合后效率更高。

4)试件BU1和BU2的荷载-挠度曲线上升段比较陡峭,这表明UHPC有效提高了梁的初始刚度和屈服后刚度。这是因为乱向分布的钢纤维横跨裂缝,可有效减缓裂缝发展,使得由于裂缝发展导致的刚度降低得到减缓。同时由于“桥联作用”,钢纤维承受了梁底部分拉应力,提高了梁的抗拉能力,从而显著增加了开裂荷载。与试件BN1和试件BN2相比,试件BU1和试件BU2的极限荷载增加了31.5%和36.3%。与等配筋率的NC梁相比,UHPC梁受弯承载力得到显著增加,这表明UHPC有效承担了受拉区的拉应力和受压区的压应力。

5)超高强钢筋NC梁在受拉钢筋屈服后,荷载基本保持不变,但跨中挠度迅速增长。而超高强钢筋UHPC梁在受拉钢筋屈服后,荷载仍然出现缓慢的增长,这主要是由于UHPC提供了梁的承载力,使梁在高荷载水平下跨中挠度呈现缓慢增长,其屈服后稳定变形相比超高强钢筋NC梁显著提升。

3.2 混凝土应变分析

混凝土和受拉钢筋的应变测量是梁的延性控制和受弯承载力设计的重要依据。图6给出了试件沿跨中截面高度的混凝土应变分布。由于试件开裂后,穿过应变片的裂缝会导致混凝土应变数据溢出,所以本试验混凝土应变数据根据梁反面的应变测点测得。超高强钢筋UHPC梁和超高强钢筋NC梁的混凝土应变沿梁高度基本呈线性分布,符合平截面假设。

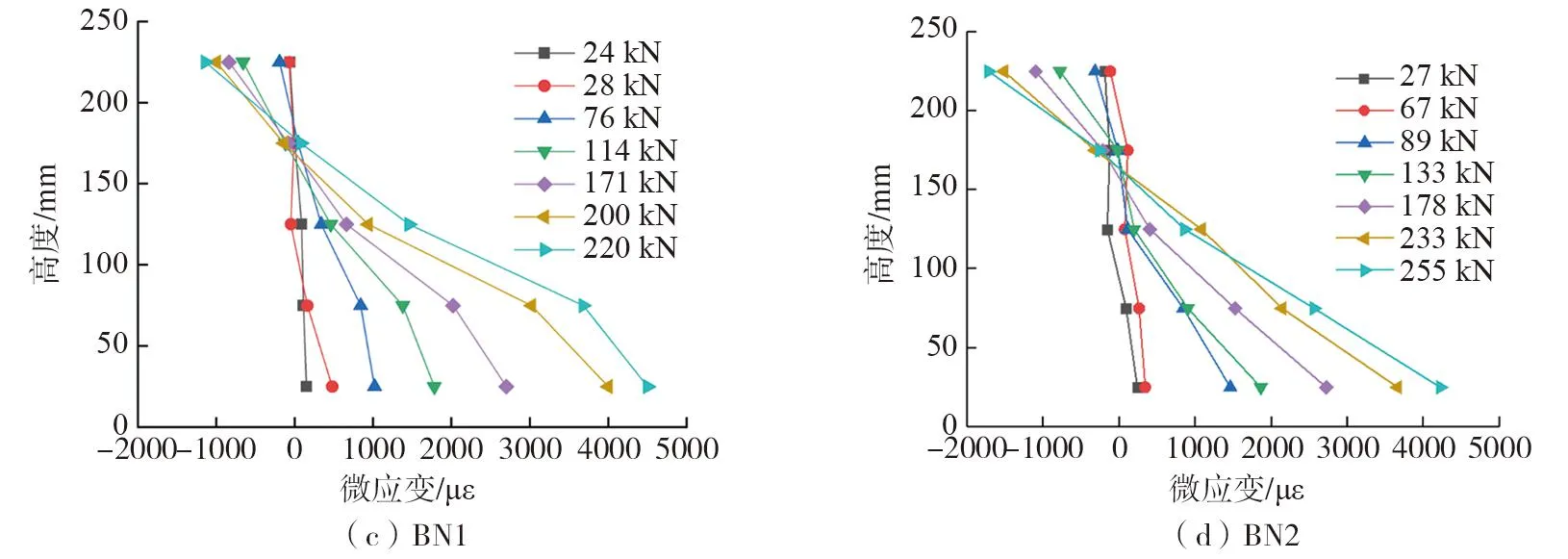
图6 跨中截面沿梁高方向的混凝土应变分布曲线Fig. 6 Strain distribution curves of concrete along the beam height in the mid span

3.3 纵向受拉钢筋应变分析

图7显示了在跨中截面荷载与受拉钢筋应变之间的关系。在初始开裂之前,受拉钢筋应变处于较低水平,约为200 με。开裂后,应变随荷载的增加而迅速增加。对于NC梁,在受拉钢筋屈服后,应变急剧增加,直至混凝土在受压区压碎。对于UHPC梁,当受拉钢筋屈服时,应变增加幅度发生变化。除高配筋率UHPC梁外,其余梁中纵筋均屈服,并达到极限拉应变。

图7 受拉钢筋应变分布曲线Fig. 7 Strains of tension reinforcement bars

4 国外规范梁受弯承载力计算公式

规范ACI 318[22]规定UHPC梁正截面承载力计算方法可以与忽略抗拉强度的普通强度混凝土梁承载力计算相同。UHPC压缩应力用一个等效的矩形应力块来表示,如图8(b)所示,式(1)为ACI 318建议的梁受弯承载力计算方法。这种方法可能会导致计算结果偏保守。

图8 相关文献提出的应力分布图Fig. 8 Stress distribution of relevant literature

(1)

(2)

式中:a为等效矩形应力块的深度;As为受拉钢筋截面面积;d为截面有效高度;fy为受拉钢筋屈服强度。

(3)

a=β1c

(4)

(5)

(6)

(7)

(8)

式中:fc和ft分别为UHPC的抗压强度和抗拉强度;σfs为钢纤维屈服应力;lf和df分别为钢纤维长度和直径;εf为理论弯矩强度下钢纤维的拉伸应变;Efs为纤维弹性模量。

联邦公路管理局(FHWA)的一份报告[24]中也给出了矩形UHPC梁受弯承载力的计算方法,如式(9)和式(10)所示,应力分布如图8(d)所示。

(9)

(10)

文献[25]提出了估算EUHPC的方程:

(11)

从国内外相关文献[3, 5, 6, 8, 26-31]中选取43根UHPC梁,每根梁的受弯承载力试验值与规范计算值之比如图9所示,其中Mexp为试验值,MACI318、MACI544、MFHWA分别为相关规范计算值。ACI 318给出的值小于试验结果,这是因为在这种方法中忽略了混凝土的抗拉能力。ACI544和FHWA方法考虑了受拉区混凝土的抗拉作用,试验值与计算值之间的偏差分别为11%和12%。上述规范中受弯承载力计算值与试验值偏差较大,因此需要提出一个适用于UHPC梁的正截面受弯承载力计算公式。

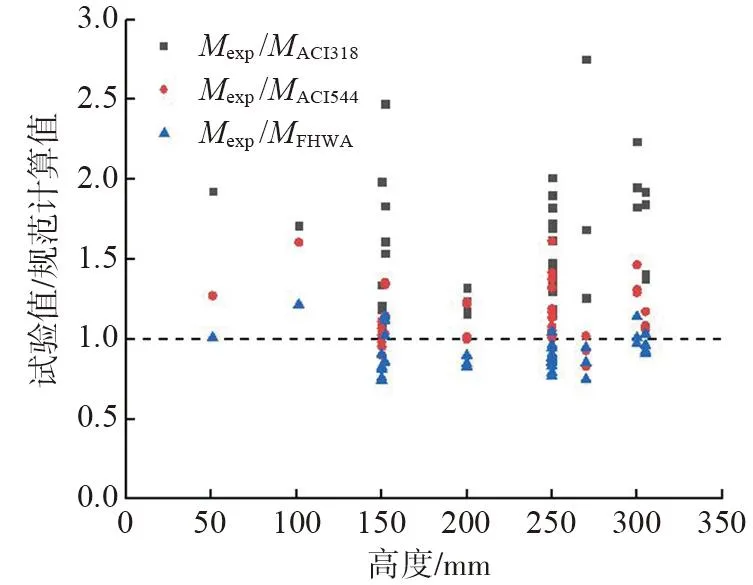
图9 受弯承载力试验值与规范计算值之比Fig. 9 Experimental-to-predicted flexural capacity ratio

5 UHPC梁正截面承载力计算

5.1 基本假定

由于UHPC梁开裂后,钢纤维的“桥联作用”仍可承受一定的拉应力,所以UHPC梁正截面受弯承载力计算时需考虑UHPC的受拉贡献。基本假定如下:①符合平截面假设;②纵向钢筋的应力-应变关系采用理想弹塑性模型;③受拉钢筋和UHPC之间不发生滑移。

5.2 受弯承载力计算

为了简化UHPC加固梁的计算,将受压区和受拉区混凝土的应力分布简化为矩形分布代替理论应力图形。其等效代换原则为受压区混凝土的应力合力大小不变且合力作用点相同。UHPC梁的应力和应变分布如图10所示。

图10 应变和等效矩形应力分布图Fig. 10 Strain and equivalent rectangular stress diagrams

根据弯矩平衡条件,得到以下2个平衡方程:

(12)

式中:x为等效受压区高度;As为纵向受拉钢筋截面面积;as为受拉钢筋合力点到受拉区域边缘的距离;α和β为等效矩形应力图系数,根据相关标准[23,32],α=0.85,β=0.74。

联立上述公式,可得到受压区高度x的表达式为:

(13)

(14)

由式(13)得到受压区高度x,将x代入式(12),并根据试验结果反推得出等效系数k=0.59。

对于矩形截面梁,设计规范通常将受拉区拉应力大小取为受拉区面积和等效系数k的乘积,等效系数k取值范围不大于1.0[33-35]。影响梁受弯承载力的参数主要包括配筋率和梁高,当配筋率较小时,系数k几乎保持不变[11]。为了验证本文提出的受弯承载力简化计算方法的准确性,选取43根UHPC试验梁(纵向受拉钢筋标准屈服强度为400～500 MPa)进行验证,图11显示了UHPC梁受弯承载力试验值与计算值的比值随梁截面高度的变化情况,Mcal为按本文简化方法得到的计算值。由图11可知,当截面高度较小时,k取为0.59时低估了梁的抗弯承载力,这是因为梁截面高度减小,k取值应增大,这是因为加载到极限状态时,梁的弯曲裂缝宽度减小,受拉区能承担更大的拉应力。也就是说,系数k与梁高h成反比。根据本文提出的计算方法,试验值与计算值之比的均值为1.1885,标准差为0.1542,变异系数为0.1297。可见,本文提出的UHPC梁正截面受弯承载力计算方法适用性较好,且与上述相关规范相比,计算结果较为精确。

图11 受弯承载力试验值与计算值对比Fig. 11 Experimental-to-predicted flexural capacity ratio

6 结论

1)UHPC可延缓试件裂缝的发展,与NC梁相比,超高强钢筋UHPC梁裂缝出现晚,宽度小,数量多而密,该梁的荷载变形在受拉钢筋屈服后仍缓慢增长,而NC梁受压区混凝土在钢筋屈服后发生大面积压溃而破坏。

2)UHPC的使用和配筋率的提高可有效提高试件的初始刚度和承载能力。同样配筋率从1.59%提高到1.88%,UHPC梁的屈服荷载和极限荷载分别提高27.8%和17.4%,而NC梁的屈服荷载和极限荷载仅提高18.7%和13.3%,表明超高强钢筋与UHPC结合效率更高,可以充分发挥两者的优势。

3)ACI544和FHWA方法考虑了UHPC的抗拉作用,能较好地预测UHPC梁的极限受弯承载力;用于普通混凝土受弯承载力计算的ACI318方法会导致计算过于保守。

4)基于超高强钢筋UHPC梁平截面假定,考虑UHPC的拉伸贡献,建立了超高强钢筋UHPC梁极限受弯承载力计算公式,对比43根UHPC梁试验结果与计算结果,两者吻合较好。