带肋拱形抗爆门的振动基频等效计算方法

田志敏,王思达,董尚委,曹兴伟

(军事科学院国防工程研究院,北京 100850)

0 引言

带肋拱形抗爆门具有优良的抗高强爆炸冲击波性能,通过选用高强金属材料并合理优化带肋拱的结构构造与设计参数,这种带肋拱形抗爆门可以抵抗峰值达数十兆帕的核爆炸冲击波荷载作用,在防爆安全领域具有广泛应用前景。但另一方面,在高强爆炸冲击波作用下,抗爆门的冲击振动十分强烈,门的振动加速度峰值可达千个g以上。因此, 即使能经受住爆炸冲击波作用不产生结构破坏,抗爆门的冲击振动也可导致门的驱动控制系统失灵[1-2];因此,需要深入研究抗爆门的振动特性,提出其振动理论分析方法及振动的控制措施[3-4]。

带肋拱形抗爆门一方面由于在拱形门内表增设了加强肋,其振动分析比等截面拱形抗爆门的振动分析更为复杂,另一方面抗爆门支撑在门框上,因支撑条件不同,抗爆门在爆炸冲击波作用下的受力状态及振动特性也不同。对于顶、底和两侧边采用不同支撑方式的拱形抗爆门的振动分析,由于问题较为复杂,目前主要采用有限元方法数值求解[5-6],但有限元分析对设计人员的计算技能要求较高。因此,工程设计部门都希望提出更为实用的简化计算方法。

带肋拱形抗爆门振动特性的简化分析方法以往缺乏研究,主要是针对无肋的等截面拱结构的基频计算问题[7-10],但带肋拱由于肋的加强改变了结构的刚度、承载性能及质量分布等特性,它的基频不能直接按无肋的等截面拱结构基频计算方法计算。为满足工程设计需要,根据两侧支撑带肋拱形抗爆门的平面内挠曲振动特性,将带肋拱形抗爆门等效为等截面拱形抗爆门,研究提出了带肋拱形抗爆门的等效等截面拱参数和反对称振动基频计算方法,同时讨论了影响基频的主要因素及等效计算方法的适应条件。

1 带肋拱形抗爆门的平面内挠曲振动模型

左、右两侧边支撑的带肋拱形抗爆门的具体构造如图1所示,抗爆门的有限元网格模型如图2(a)所示。有限元计算表明,拱形抗爆门的基频振动主要呈现反对称形式如图2(b)所示,计算参数如表1和表2所示。在水平向冲击波荷载作用下,主要呈现沿冲击波传播方向的挠曲振动反应;可将该门先等效为等截面拱形抗爆门,然后按过门半高处横截面的平面内挠曲振动模型分析。

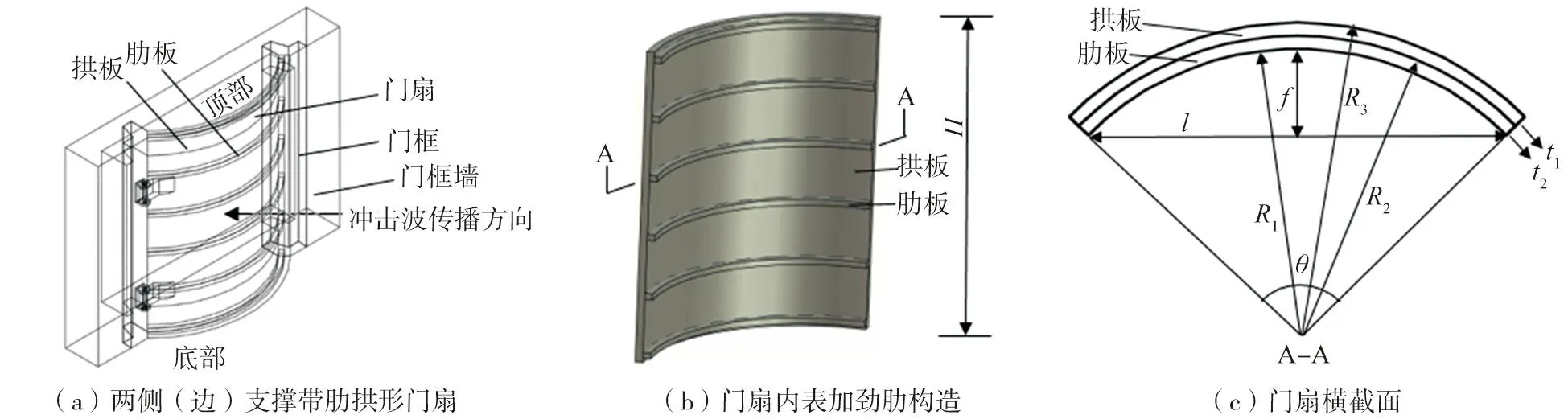
图1 立转式带肋拱形抗爆门示意图Fig. 1 Schematic diagram of a vertical rotating blast resistance arched door with strengthening ribs

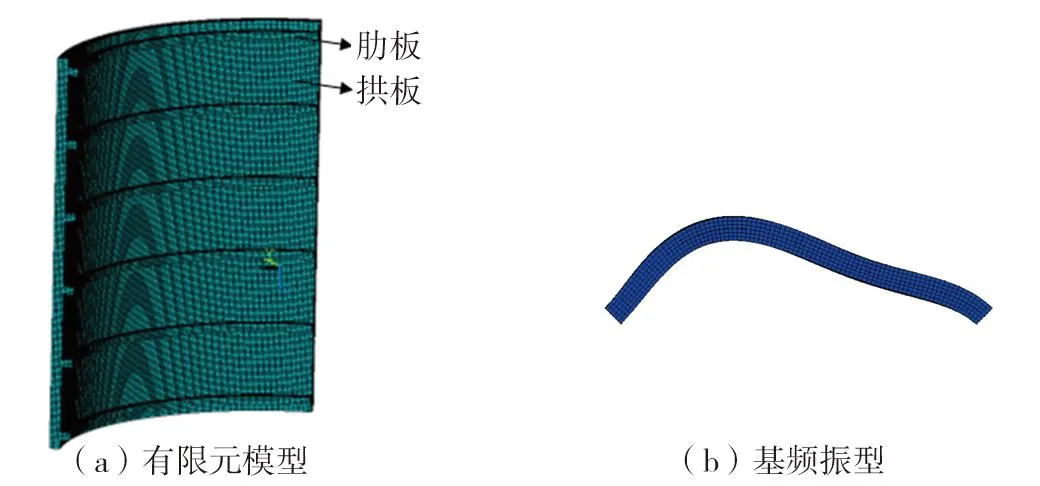
图2 带肋拱形抗爆门有限元计算结果Fig. 2 Finite element calculation results of a blast resistance arched door with strengthening ribs

表1 材料参数Table 1 Material parameters

表2 几何参数及边界条件Table 2 Geometric parameters and boundary conditions

1.1 带肋拱形抗爆门的等效等截面拱参数计算

设带肋拱的拱板内、外径分别为R2、R3,肋板内径为R1,拱的圆心角为θ,拱板和肋板厚度分别为t1和t2。设等效等截面拱的外径R3、圆心角θ和高度H与带肋拱相同,如图3所示,假设带肋拱形抗爆门和等效等截面拱形抗爆门具有相同的平面内挠曲振动特性,则可分别推导出等效等截面拱形抗爆门的内径Re和质量密度m的计算公式为:

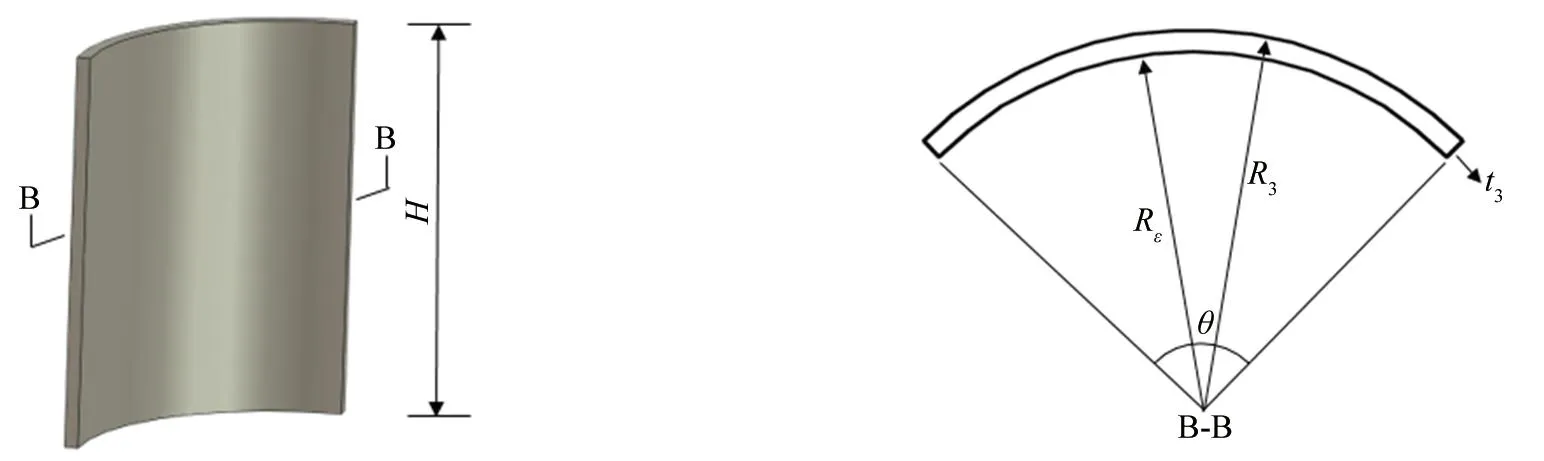
图3 等效等截面拱形抗爆门示意图Fig. 3 Schematic diagram of equivalent cross section for constant section blast resistance arched door

(1)

式中:t3为等效等截面拱形抗爆门拱板厚度;yc为抗爆门沿顶底方向带肋拱板组合截面的形心距;a为肋板宽度;n为肋板数量;ρ为材料密度。

1.2 等效等截面拱的反对称振动基频计算

将带肋拱形抗爆门等效为等截面拱形抗爆门后,可按过门半高处横截面的平面内挠曲振动模型分析门的自振频率[11-13]。圆拱发生面内屈曲后,微元ds=Rdφ在径向荷载pr和切向荷载ps以及内力N、Q、M的作用下处于平衡状态如图4所示。由切向力、径向力和弯矩的平衡条件得出:

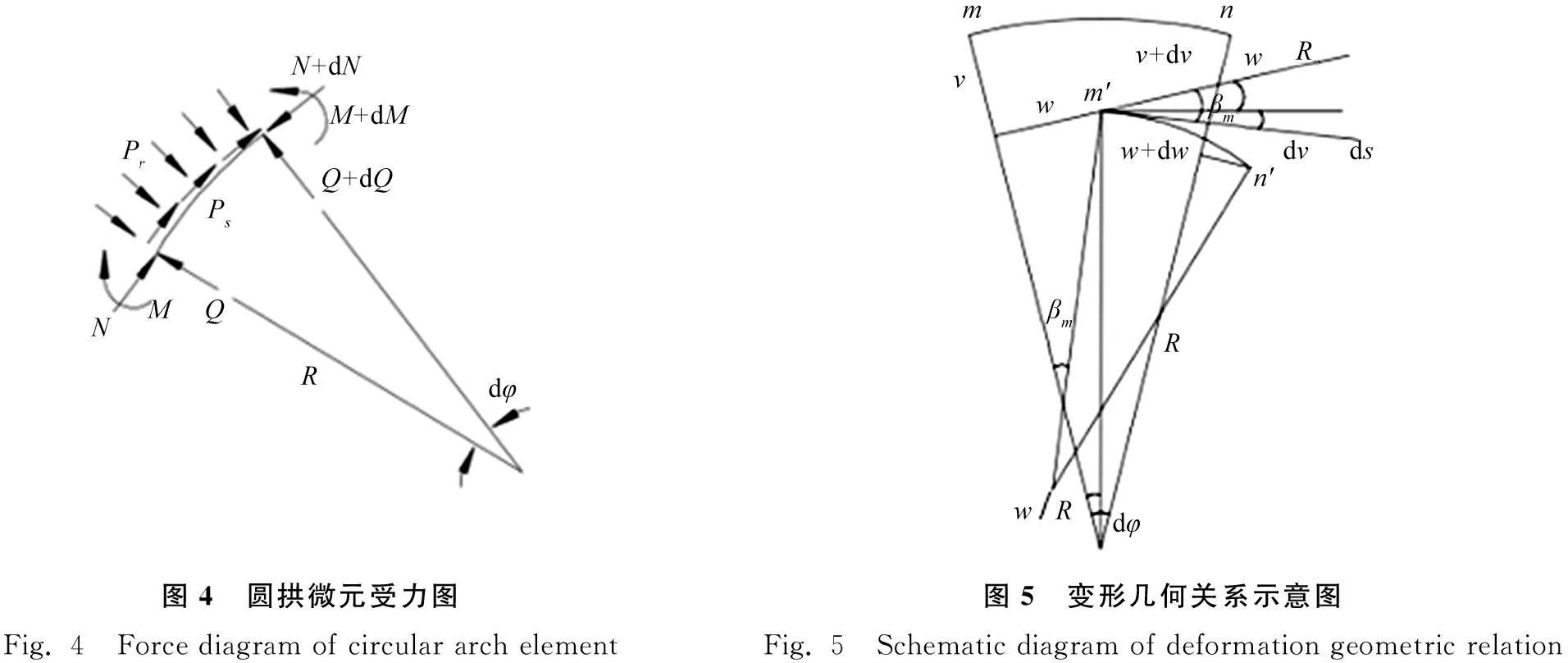
图4 圆拱微元受力图Fig. 4 Force diagram of circular arch element图5 变形几何关系示意图Fig. 5 Schematic diagram of deformation geometric relation

(2)

拱微元mn在平面内挠曲变形后至新的位置m′n′,如图5所示。设m点的径向和切向位移分别为v和w。由图可知:由位移v引起的转角为dv/ds;由位移w引起的转角近似取为w/R,所以在v和w共同影响下截面的转角为:

(3)

可得微元ds的曲率改变量即单位长度转角增量为:

(4)

微元ds由于切向位移w引起的伸长为dw;由于径向位移引起的伸长为(R-v)dφ-Rdφ,即-vdφ,故微元ds单位伸长为:

(5)

弯矩M和轴力N与挠曲率K和伸长率ε的关系为:

(6)

式中:EJ和EF分别为拱截面在拱平面内的抗弯刚度和抗拉(压)刚度。将式(4)、式(5)、式(6)代入式(2)可得圆弧拱的平面挠曲的弹性平衡微分方程:

(7)

根据能量守恒原理,在拱的自振过程中最大变形能等于最大动能,即:

Umax=Tmax

(8)

计算变形能时只考虑弯曲变形,忽略轴向变形和剪切变形[14-16],则:

(9)

振动是简谐的,设

(10)

将式(10)代入式(9),根据瑞莱法原理,由Umax=Tmax可得频率公式为[8-10]:

(11)

对于采用两侧嵌固支撑方式的带肋拱形抗爆门,在满足拱端位移为0、径向速度为0的边界条件及拱轴不变形条件时,可求得反对称基频计算公式为[17-18]:

(12)

式中:Ω为频率系数,如图6所示;α为拱弧全长对应的半圆心角(α=0.5θ);l为圆拱计算跨度;E为圆拱材料受压弹性模量;J为单位宽圆拱截面惯性矩;m为单位长度圆拱质量。

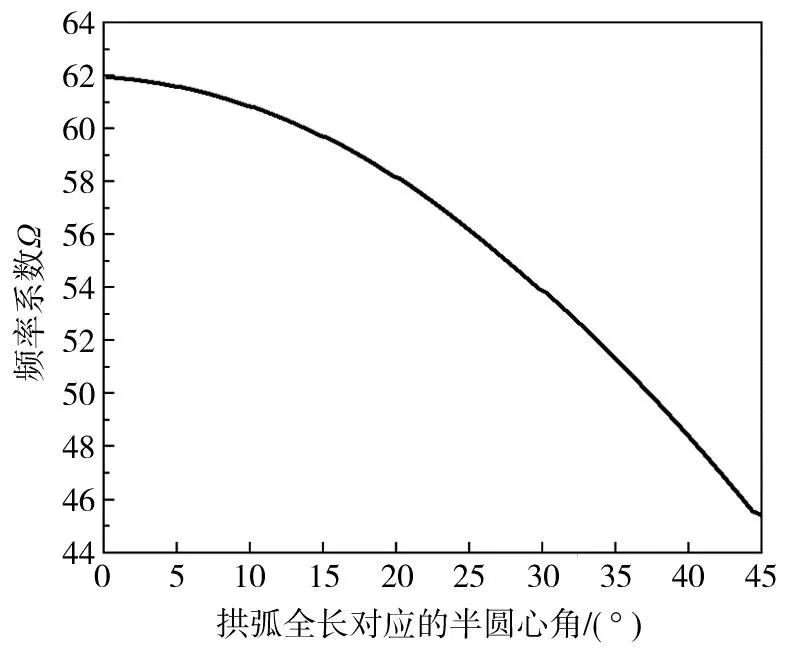
图6 频率系数图Fig. 6 Diagram of frequency coefficient

等效等截面拱形抗爆门外径为R3,内径为Re。其单位宽圆拱截面惯性矩J,单位宽圆拱体积V,单位宽圆拱弧长S,单位长度圆拱质量m计算公式为:

(13)

式中:b为圆拱截面宽度;ρ为拱形抗爆门所用材料密度。

式(1)、式(12)、式(13)适用于采用两侧嵌固支撑方式的带肋拱形抗爆门[19-20]的反对称基频计算。

2 基频的主要影响因素及计算结果讨论

2.1 肋板与拱板厚度比对基频的影响

带肋拱形抗爆门等效为等截面拱形抗爆门后,振动基频可由式(12)算出,将式(13)代入式(12)可得:

(14)

式(14)表明,频率系数Ω仅与拱弧全长对应的半圆心角有关,而弹性模量E和材料密度ρ为定值,因此振动基频ω与t3/l2呈正比,即:

(15)

若拱板厚度t1不变,肋板与拱板厚度比t2/t1增加,则t2增加;使得t3增加、l减小,则t3/l2增加,ω变大;振动基频随肋板与拱板厚度比变化的关系曲线如图7所示。

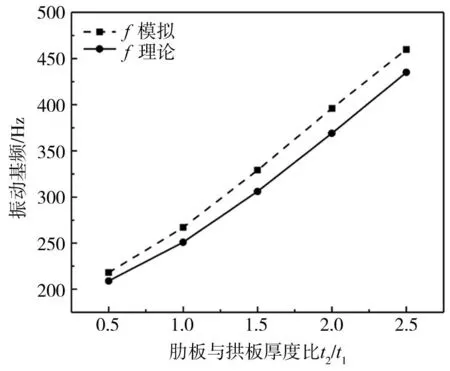
图7 振动基频与t2/t1关系Fig. 7 Relationship between the eigen-frequency and t2/t1

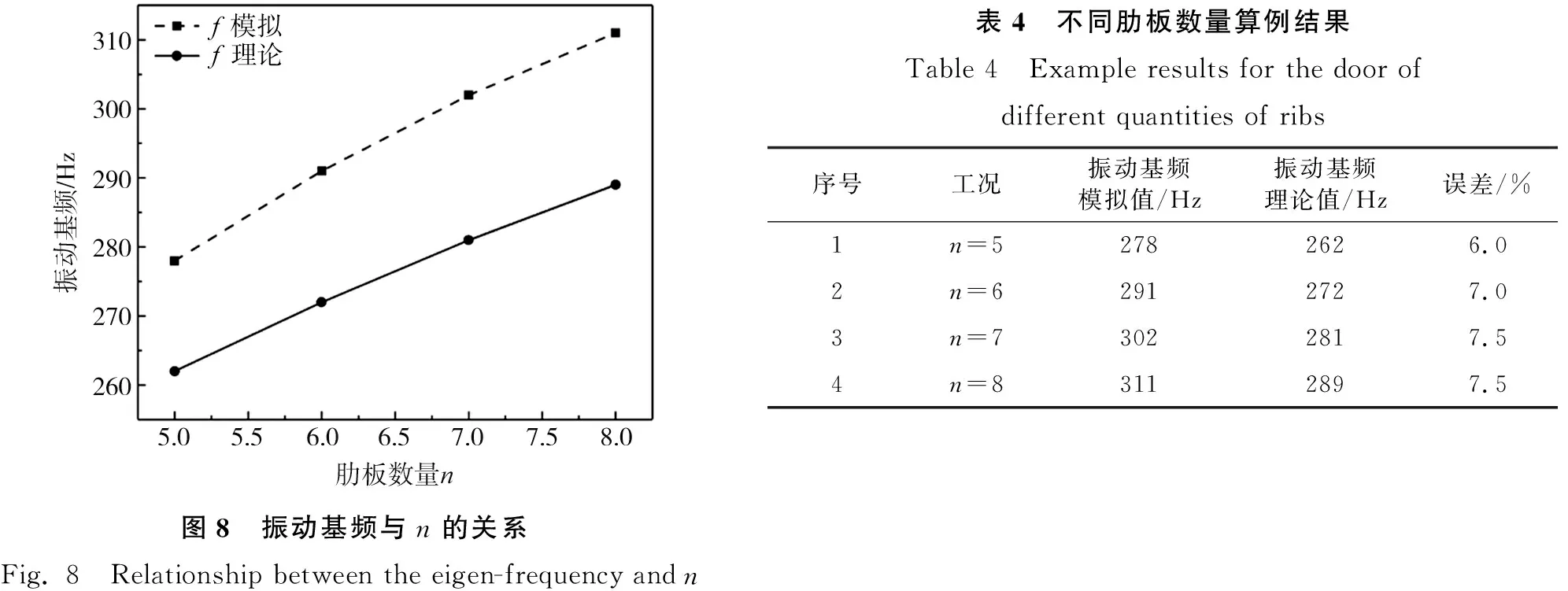
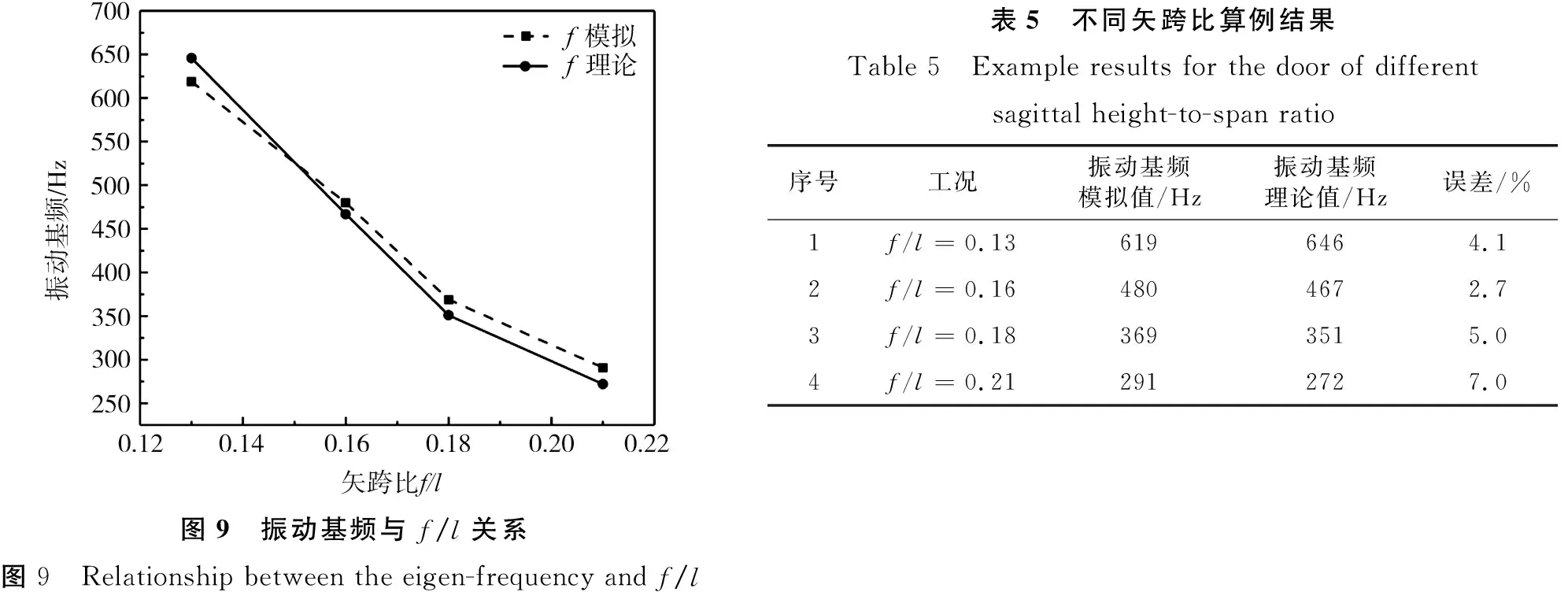
采用等效等截面拱基频计算方法得出的具有不同肋板与拱板厚度比t2/t1的带肋拱形抗爆门的反对称基频计算结果及其与有限元方法得出结果的比较如表3所示。由表可知,对于一般的带肋拱形抗爆门(0.5≤t2/t1≤2.5),在满足厚跨比0.03

表3 不同肋板与拱板厚度比算例结果Table 3 Example results for the door of different thickness ratios between ribs and arch plates

2.2 肋板数量对基频的影响

由式(1)、式(12)、式(13)可知,肋板数量n增加,则等效等截面拱形抗爆门拱板厚度t3增加;ω与t3/l2的函数关系可简化为:

(16)

因为t3

图8 振动基频与n的关系Fig. 8 Relationship between the eigen-frequency and n表4 不同肋板数量算例结果Table 4 Example results for the door of different quantities of ribs序号工况振动基频模拟值/Hz振动基频理论值/Hz误差/%1n=52782626.02n=62912727.03n=73022817.54n=83112897.5

具有不同的肋板数量的带肋拱形抗爆门的反对称基频计算结果及其与有限元计算结果的比较如表4所示。由表可知,一方面,随着肋板数量增加,带肋拱形抗爆门的反对称基频增大;另一方面,等效等截面拱基频计算方法与有限元计算方法得出的基频计算结果基本一致,二者得出的计算结果误差也在8.0%以内。

2.3 拱的矢跨比对基频的影响

矢跨比f/l增加,则抗爆门对应圆心角θ增加。由式(16)得:矢跨比f/l增加,θ增加,ω减小;振动基频与矢跨比变化的关系曲线如图9所示。

图9 振动基频与f/l关系图9 Relationship between the eigen-frequency and f/l表5 不同矢跨比算例结果Table 5 Example results for the door of different sagittal height-to-span ratio序号工况振动基频模拟值/Hz振动基频理论值/Hz误差/%1f/l=0.136196464.12f/l=0.164804672.73f/l=0.183693515.04f/l=0.212912727.0

具有不同矢跨比的带肋拱形抗爆门的反对称基频计算结果及其与有限元计算结果的比较如表5所示,由表可知,随着矢跨比增大,带肋拱形抗爆门的反对称基频减小,本文给出的计算方法与有限元方法得出的基频计算结果基本一致,二者计算结果的误差在7.0%以内。

3 结论

通过本文对带肋拱形抗爆门的振动基频计算方法研究和计算结果,可以得出如下结论:

1)两侧边支撑的带肋拱形抗爆门的基频振动主要呈现反对称形式,当满足0.5≤t2/t1≤2.5和0.03

2)肋板与拱板厚度比、肋板数量和拱的矢跨比是影响带肋拱形抗爆门反对称基频的主要因素,基频随着肋板与拱板厚度比和肋板数量增加而增大;基频随着矢跨比增大而减小。