西南地区水平向地震动设计谱参数特征分析
胡进军,石 昊,谭景阳
(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080; 2. 地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080)
0 引言
基于弹性反应谱理论的抗震设计方法是目前抗震设计应用最广泛的方法。规范抗震设计谱通常根据大量实际地震记录的反应谱进行统计,并结合工程经验加以规定[1]。设计反应谱是抗震设计的重要依据,是确定地震作用的关键,因此设计反应谱的研究一直是抗震设计研究中的重点,如对反应谱下降段的研究、曲线形式的研究,以及对设计反应谱中的地震影响系数(αmax)、特征周期和反应谱模型的修正。解决以上问题的关键便是对设计谱参数进行分析。
自20世纪40—50年代,标准反应谱与设计反应谱[2-4]在国外被提出后,国内的反应谱研究也随之起步。1958年,刘恢先[5]建议采用反应谱理论进行抗震设计。随后便在1964年抗震规范草案中采用了与场地条件相关的抗震设计反应谱理论并一直发展至今。设计反应谱参数的分析是抗震设计的重要一环,相关研究提出了三参数标定法、双参数标定法等[5-8]。近些年,学者们开始引入各种不同算法,如遗传算法、最小二乘法、模拟退火算法、差分进化算法、粒子群算法、卷积神经网络算法等[9-19]。合理的标定方法是基于地震动进行设计谱参数分析的关键,其中基于全局和邻域变异的差分进化算法(differential evolution with global and local neighborhoods, GLDE)在稳定性和精确性上有明显的优越性[18]。
我国西南地区临近印澳板块与亚欧大陆板块,处于青藏高原南、中部地震区[20],有着十余条地震带,强震频发。近年来随着强震观测台网的发展,西南地区积累了大量强震动数据。考虑到地震动存在的区域特征差异,基于实际地震动开展设计谱特征参数的研究,不仅可以比较实际不同场地反应谱参数与现行规范设计谱参数的异同,还可以为未来规范设计谱的改进和修正提供建议。郭晓云等[12]基于汶川地震记录采用最小二乘方法研究了场地条件和断层距对反应谱特征参数的影响。谭潜等[19]选取421条汶川地震主震记录对现行规范设计反应谱的长周期段进行研究,认为长周期段的取值与地震动记录的长周期特性密切相关,并给出了不同场地和不同设计地震分组时设计谱平台段(βmax)和特征周期(Tg)的取值。考虑到西南地区的区域性特征以及单次地震中地震动记录的特殊性,尽可能多地采用本地区实际地震动记录对设计谱特性进行研究是分析区域设计谱参数的关键。
本文收集整理了截至2022年底我国西南地区的强震动数据和场地资料,对地震动按场地类别和地震分组进行分类,采用改进的差分进化算法对西南地区设计谱的特征参数进行标定,分析西南地区设计谱特征参数变化以及与现行设计谱参数之间的差异。
1 西南地区强震记录及分组
1.1 数据库
本文整理了2007—2022年我国西南地区的强震动数据,包括1803次地震的14097条地震动记录,并对其进行基线校正和带通滤波处理。基于震级、场地条件、震源距、断层距、峰值加速度、设计地震分组对数据进行筛选和分类。选取的地震记录面波震级(Ms)范围为4.0≤Ms<8.0。对所有强震数据进行筛选[21-23]:剔除①非地震动波形、P波丢失、单次记录包含多个地震事件、信噪比小于3等低质量波形;②台站资料不足以进行场地分类且无其他分类依据的记录;③震源距Rhyp>300 km或者断层距Rrup>300 km的记录;④峰值加速度PGA<10 Gal的记录。为了保证记录的数量,避免统计过程中单次地震事件内的偶然误差,剔除小震(4.0≤Ms<5.0)中单次数据小于5条的记录、中震(5.0≤Ms<6.0)中单次数据小于3条的记录、中大震(6.0≤Ms<7.0)中单次数据小于2条且震源距Rhyp>60 km的记录。通过上述原则筛选得到地震事件284次,包含353个台站的4527条水平向地震动记录,相较于以往的区域性设计谱研究[12-13,19],本文数据包含了目前我国西南地区绝大多数水平向地震动记录。
1.2 地震动记录及分组
对筛选后的西南地区353个台站地震动记录进行分析,按照以下标准对台站的场地类别进行划分:①对于具有剪切波速以及覆盖层厚度数据的台站,依据GB 50011—2010《建筑抗震设计规范》进行场地分类;②对于缺少完整信息不能直接参照规范进行分类的台站,利用已知剪切波速信息进行速度梯度延拓[24],获得等效剪切波速VS30,利用场地类别转换方法[25-26]获得该台站的场地类别;③对于缺失剪切波速以及覆盖层厚度数据,无法分类的台站,参考相关场地分类的研究结果[23-24, 27-30]。按照上述原则分类后的各类场地台站数量如表1所示。

表1 各类场地台站数量Table 1 Number of stations for different site classes
本文选用近似方法逐条进行计算地震动反应谱特征周期Tg[31-32],如式(1)所示:
(1)
式中:EPV为有效峰值速度;EPA为有效峰值加速度。
由于Ⅳ类场地地震动记录数量较少,因此本文只针对Ⅰ、Ⅱ、Ⅲ类场地进行研究。最终选取出276次地震,共计3084条水平向地震动数据,按照峰值对地震动进行设计地震分组,结果如表2所示。震源深度-震级,震源距-震级和震源距-峰值加速度(PGA)的分布如图1所示。

表2 记录分组和条数Table 2 Classification and numbers of records in each group

图1 地震数据的分布图Fig. 1 Distribution of ground motion data
2 设计谱标定方法及其稳定性验证
2.1 改进的差分进化算法
通过地震动记录确定设计谱时,实际上是标定控制设计谱形状的几个特征参数以达到最佳拟合效果。应用差分进化(differential evolution, DE)算法对设计谱特征参数进行研究可以高效地锁定最优情况,从而能够清晰地分析设计谱的特征周期和平台段的变化情况[12,14,17]。谭景阳等[18]从改进的差分进化算法中挑选出兼顾稳定性和精度的GLDE算法进行设计谱特征参数标定,相比于标准DE算法获得的结果更可靠。本文应用此算法对我国西南地区数据进行设计谱特征参数标定。
采用四阶段设计反应谱拟合模型,如式(2)所示:
(2)
式中:T为结构自振周期;βmax为放大系数谱的最大值即平台段取值;Tg为与场地条件和设计分组有关的特征周期值;γ为衰减指数;T0为曲线上升段与平台段的交点;Td为下降区两段的分界点;Tm为反应谱周期的最大值,基于我国规范选取Tm值为6.0 s;η1为直线下降段的斜率调整系数;η2为阻尼调整系数,由于本文阻尼比设置为0.05,因此η1与η2分别取值为0.02和1。模型如图2所示。

图2 设计反应谱拟合模型Fig. 2 Fitting model of design response spectra
对选取的5个特征参数(T0,Tg,Td,βmax和γ)进行寻优,实质上是寻找β的最优值。为了保证搜索结果最优,选取基于最小二乘原理设定的适应度函数,如式(3)所示:
(3)
由于实际反应谱的计算结果是离散周期值,因此对其进行线性插值求得连续反应谱,再通过式(3)表示拟合的均方根误差,用以评价拟合水平:曲线拟合程度越高,F取值越小,5个参数的值便越靠近最优解。GLDE算法主要包含初始化、改进的变异操作、交叉和选择4个步骤,流程图如图3所示。

图3 GLDE算法流程图Fig. 3 Flowchart of the GLDE algorithm
步骤1:初始化。随机产生NP个均匀分布的初始解x0,j(j= 1, 2, …,NP),如式(4)所示:
(4)
式中:Xmin和Xmax分别为初始设置的极小、极大值;k1为均匀分布的随机数;X0为基于Xmin和Xmax生成的NP行5列的解矩阵,每行的x0为一个单独的解。
步骤2:变异。将第t次迭代后的解随机排列后首尾相接,即此时的第j+1行实为第1行,构成一个循环的解集,以免陷入局部的最优解从而导致计算结束。对第i个解xi用其周围的2k+1个解[xi-k,xi+k](邻域)进行表示。为产生后代vi,t,需进行变异计算,即分别由邻域解向量计算所得的Li和整体(全局)解向量计算所得的Gi进行加权计算:
(5)
式中:xp、xq、xr、xs均为随机选择的解。其中xp、xq选自邻域,xr、xs选自全局(总解集),xn-best、xp-best分别为邻域内和全局中可令计算所得的F值最小的解(即最贴近实际反应谱)。参数α、β分别设为0.7[33]。权重系数w采用自适应更新[33]进行选取,如式(6)所示:
(6)
式中:wbest是全局中令F值最小的解所对应的权重系数;wr和ws分别为式(5)中xr和xs所对应的权重系数,当wi超出界限时取最近的边界值。比例因子P设为0.7[32]。
步骤3:交叉。对于第t次迭代后的解,将步骤2之前与之后的2个解集进行如下交叉操作,即依照概率对旧解集中的解向量进行随机替换,最终产生新的向量U:
(7)
式中,本方法CR取值0.3[32];k2为从[1,5]随机选取的整数。
步骤4:选择。按照式(3)计算Ui,t和Xi,t的F值,选择二者中具有较小F值的解矩阵作为下一代的初始解输入步骤(2),继续进行下一次迭代。
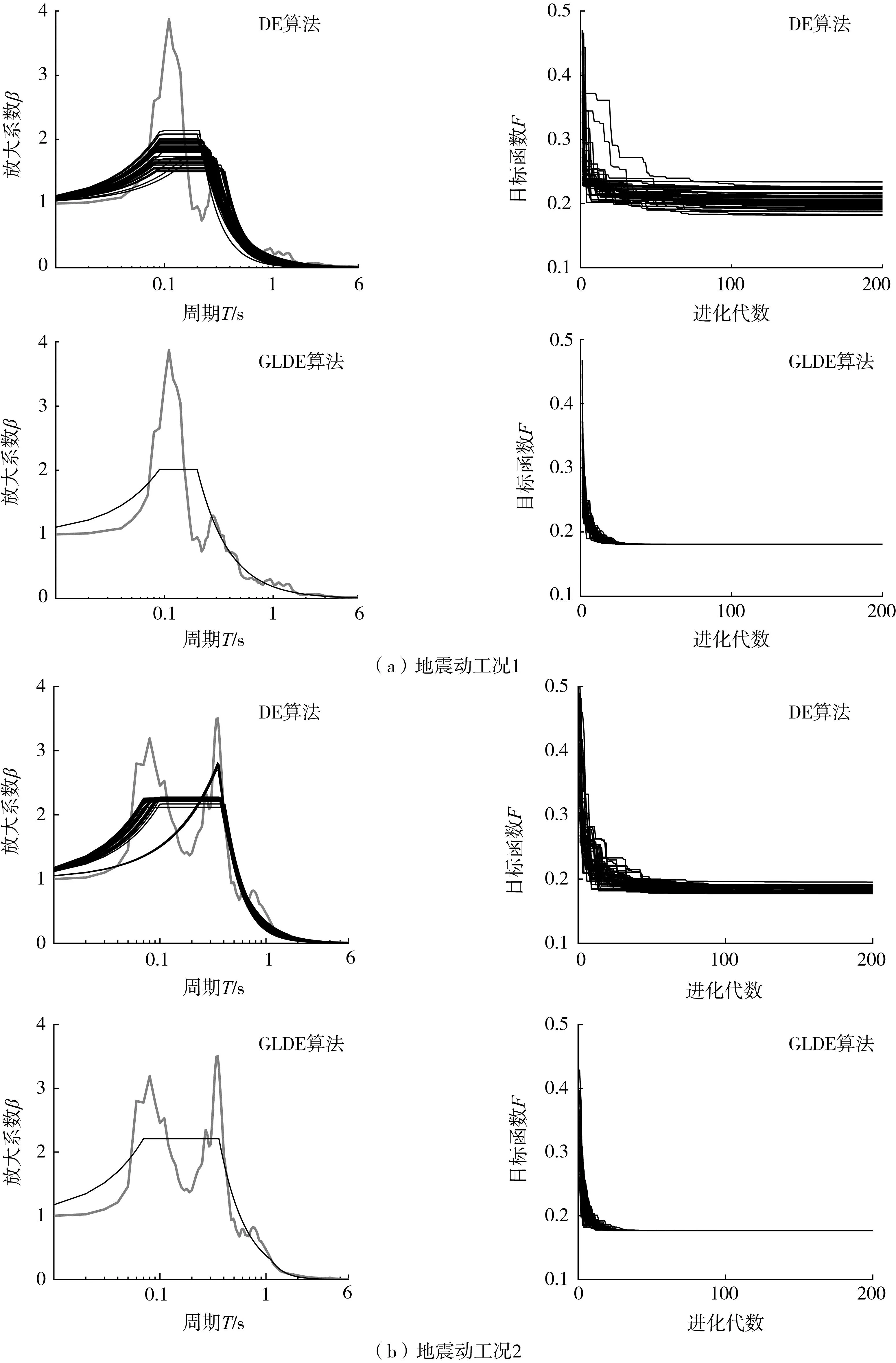
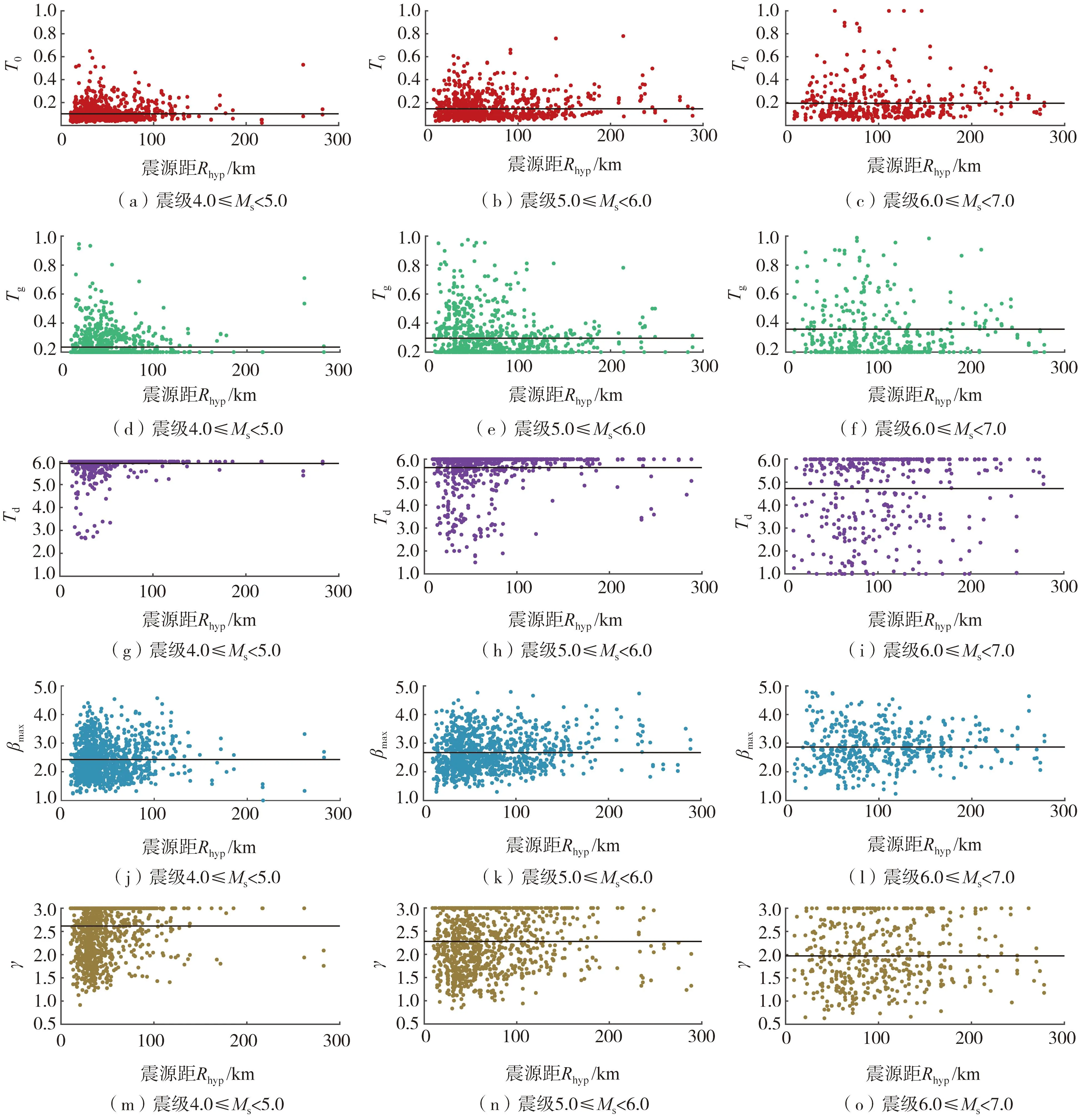
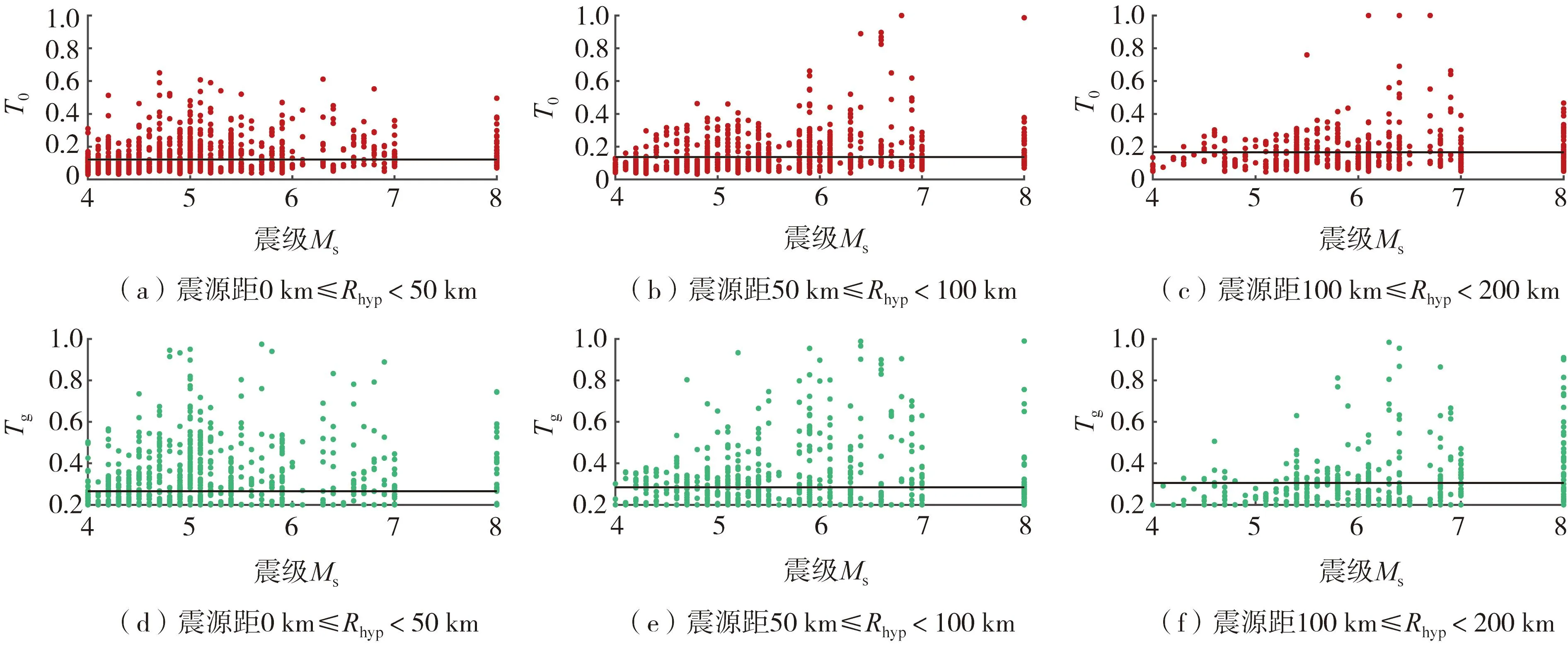
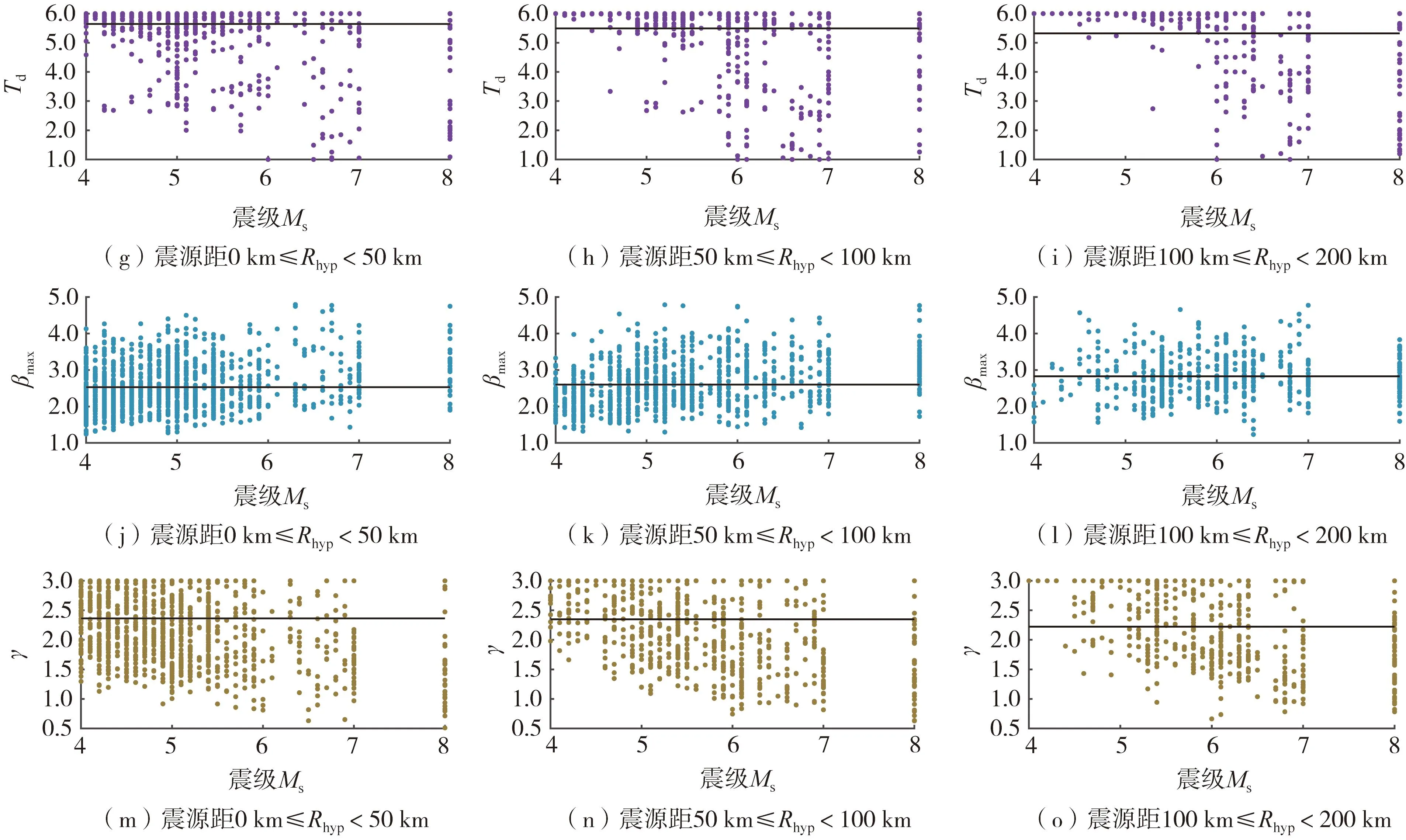
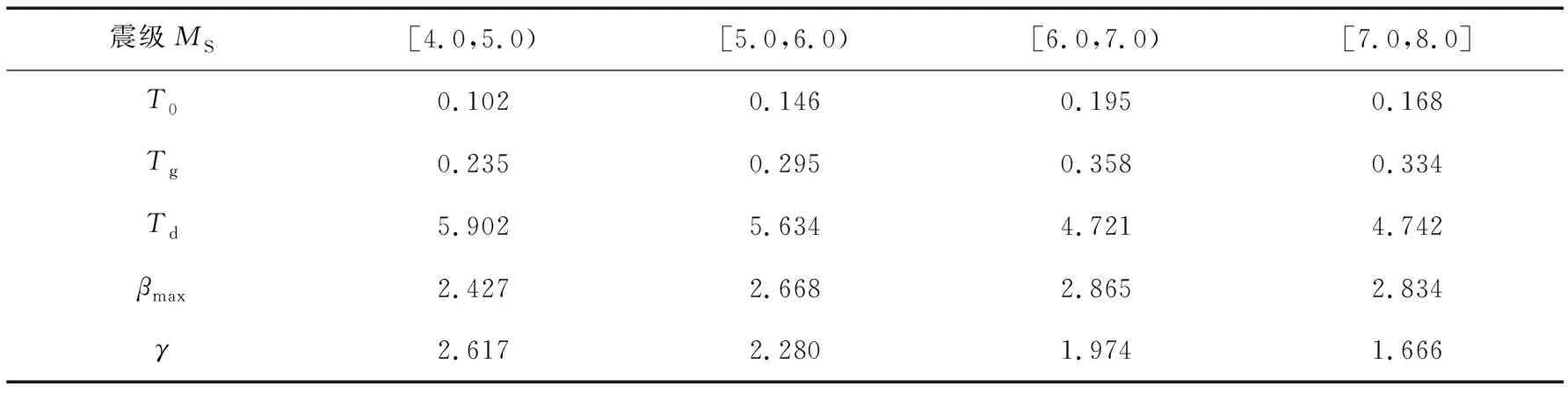
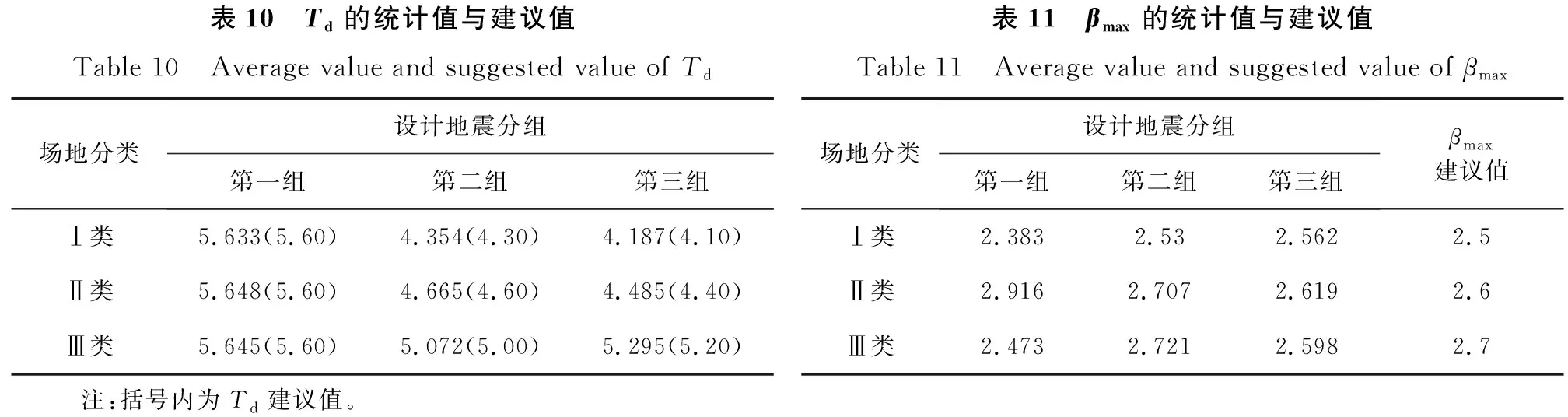
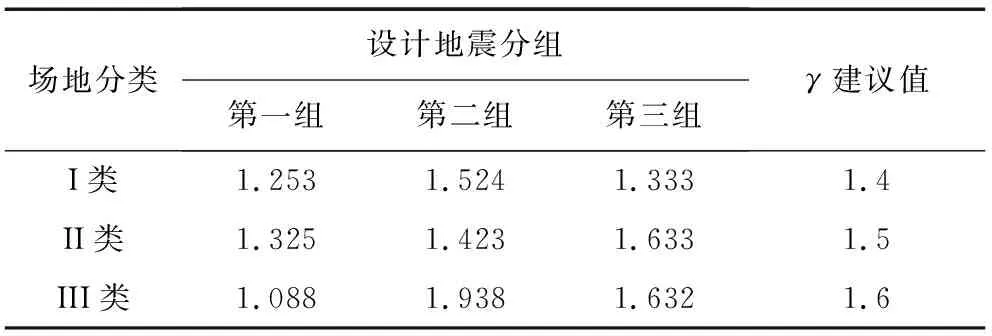
设计谱标定前,需设置F的目标值F0以及最大进化代数Gmax。当满足F 对选取的全部地震动数据分别用标准DE算法与GLDE算法进行标定并比较,以验证GLDE算法的稳定性。5个特征参数的初始范围设置为:T0∈(0.02,0.5)、Tg∈(0.1,1.0)、Td=5Tg且Td∈(1.5,6)、βmax∈(1,4)、γ∈(0.2,2)。算法参数按照效率最高的方案进行选取[32]。 图4(a)、(b)为对随机选择的2条西南地区的反应谱采用标准DE算法和GLDE算法进行的标定结果。对于图4(a)、(b),左侧为分别使用DE与GLDE算法进行标定时的结果变化趋势,每一次迭代都对应着图中的一条设计谱,同时在右侧对应着一条目标函数F的变化曲线。由图可知,与GLDE算法相比,DE算法的设计谱曲线集和目标函数集多且杂,说明DE算法搜寻结果的速度慢,并且容易陷入局部最优解的循环。而GLDE算法的曲线集很简洁,说明其搜寻最优解的目标函数会在更早的进化代数趋于稳定,同时并没有由于达到局部最优解而产生早熟或停滞,对设计谱的标定过程不存在结果不稳定的现象。相比于DE算法[13,15],GLDE算法的结果明显更为可靠,给出的结果也更准确。 图4 GLDE方法标定反应谱的验证Fig. 4 Validation of applying the GLDE calibration method to the response spectra 将基于GLDE算法的计算结果分别按照震级与震源距进行分组:震级分为[4.0,5.0)、[5.0,6.0)、[6.0,7.0)和[7.0,8.0]共4组,震源距分为[0,50)km、[50,100)km、[100,200)km、[200,300]km共4组。部分设计谱特征参数随震源距、震级的变化趋势分别如图5和图6所示。每个参数在每个分组内的平均值用黑线表示,具体数值如表3和表4所示。 图5 不同震级分组内特征参数随震源距变化的趋势Fig. 5 Trend of characteristic parameters with source distance within different magnitude groups 图6 不同震源距分组内特征参数随震级变化的趋势Fig. 6 Trend of characteristic parameters with magnitude within different source distance groups 表3 特征参数按震级分组的平均值Table 3 Average value of characteristic parameters grouped by magnitude 表4 特征参数按震源距分组的平均值Table 4 Average value of characteristic parameters grouped by hypocentral distance 由图5、图6可知,5个参数都有着明显的单调趋势。随着震级和震源距的增加,第一拐点T0、特征周期Tg以及放大系数最大值βmax均逐渐增大,而第三拐点Td和衰减指数γ在逐渐减小。随着震级与震源距的增大,设计谱的第一、第二拐点均向长周期段移动,第三拐点向短周期段移动,平台段会有所上升,同时下降段的衰减趋势将越发平缓。 在现行规范中,第三拐点周期Td为5倍的特征周期Tg,但在标定时,Td结果趋向于长周期,部分记录结果在标定周期内甚至不存在第二个下降段。于是本文针对不同震级分组、震源距分组、设计地震分组及场地分类对Td/Tg的平均值进行计算,如表5~表7所示。由计算结果可见,与规范中的Td=5Tg相比,各分组中的Td/Tg平均值基本都大于5,且该比值随着震级、震源距、设计地震组别以及场地分类的增加呈减小趋势。基于标定的结果,Tg至Td段应当适当延长,不同场地不同分组下的Td的取值范围均应该在5 s左右。 表5 不同震级分组内Td/Tg平均值Table 5 Average Td/Tg within different magnitude groups 表6 不同震源距分组内Td/Tg平均值Table 6 Average Td/Tg within different source distance groups 表7 不同设计地震分组及场地分类Td/Tg平均值Table 7 Average Td/Tg values for different design earthquake groups and site classifications 为整体比较西南地区设计谱特征参数与规范设计谱特征参数的异同,通过放大系数谱对二者进行直接的比较,如图7所示。图7基于不同的设计地震分组与场地条件,展示了GLDE算法标定结果、我国规范设计谱与实际观测记录的放大系数平均谱之间的对比关系。 图7 GLDE标定谱、现行规范设计谱与实际数据平均放大系数谱的对比Fig. 7 Comparison of GLDE spectra, design spectra and the mean amplification factor spectra 各特征参数的统计值如表8~表12所示。与规范设计谱相比,基于西南数据计算的放大系数最大值βmax的取值更大,始终略高于规范谱的平台值。对于规范中所提出的不小于大样本容量平均值的设计理念,有着更好的保证率,并且没有偏大很多。第一拐点T0是设计谱上升段与平台段的交点,特征周期Tg是设计谱平台段与下降段的交点,二者共同规定着设计谱的平台段。由标定结果可知,随着场地类别与设计组别的增加,T0与Tg均增大,即平台段有着向长周期移动的趋势,更符合每组中反应谱峰值的移动趋势。下降段拐点Td偏向长周期,基本分布在4~5.5 s,说明速度控制段的长度偏长,与规范谱中的5倍Tg有明显的区别。衰减指数γ始终大于规范谱中的取值,在长周期段的衰减趋势明显大于规范谱,与平均谱有着更好的拟合效果。 表8 T0的统计值与建议值Table 8 Average value and suggested value of T0场地分类设计地震分组第一组第二组第三组T0建议值Ⅰ类0.1020.1770.2010.10Ⅱ类0.1210.1830.3230.15Ⅲ类0.1380.3530.4150.20表9 Tg的统计值与建议值Table 9 Average value and suggested value of Tg场地分类设计地震分组第一组第二组第三组Ⅰ类0.255(0.25)0.456(0.45)0.806(0.80)Ⅱ类0.318(0.35)0.598(0.60)1.091(0.90)Ⅲ类0.412(0.45)0.716(0.75)1.009(1.10) 注:括号内为Tg建议值。 表10 Td的统计值与建议值Table 10 Average value and suggested value of Td场地分类设计地震分组第一组第二组第三组Ⅰ类5.633(5.60)4.354(4.30)4.187(4.10)Ⅱ类5.648(5.60)4.665(4.60)4.485(4.40)Ⅲ类5.645(5.60)5.072(5.00)5.295(5.20) 注:括号内为Td建议值。表11 βmax的统计值与建议值Table 11 Average value and suggested value of βmax场地分类设计地震分组第一组第二组第三组βmax建议值Ⅰ类2.3832.532.5622.5Ⅱ类2.9162.7072.6192.6Ⅲ类2.4732.7212.5982.7 表12 γ的统计值与建议值Table 12 Average value and suggested value of γ 对于长周期段的设计反应谱取值,不同学者之间存在争议[34-39]:一部分学者认为,为保证设计地震的最小剪力系数,从而满足结构设计的安全性,应当对长周期段进行人为提高以提升安全概率;而另一部分学者认为长周期段未考虑场地条件便进行了人为修正,长周期结构在地震作用下计算的位移值偏大,在设计时很难通过提升刚度来满足最小剪力系数的要求,从而造成设计上与施工上的浪费,因此应该适当下调。本文基于大量西南地区实际地震动数据的标定结果可见:在长周期段的衰减趋势明显大于规范谱,因此对长周期结构按照目前规范谱进行的设计可能会偏于保守。 为了增加结果的保证率,利用标准差增加标定结果的置信区间[15]:对于Td,其取值为本组数据的平均值减去该组数据的标准差;而对于Tg,其取值为本组数据平均值加上该组数据的标准差。对于T0、β与γ共3个参数,按照不同的场地分类以记录数量进行加权平均,对计算结果取整给出便于工程采用的建议取值。Tg的取值与场地特征周期相关、Td的取值与Tg相关,因此对Td与Tg基于不同场地分类与不同设计分组分别给出建议值,各特征参数的建议值如表8~表12所示。 将本文给出的建议值分别与基于汶川、云南地震记录给出的设计谱参数建议值[19, 40](图中分别用文献[19]、文献[40]表示)、中国规范设计谱和分组反应谱平均值进行比较,对比结果如图8所示。 与其他设计谱相比,本文给出的设计谱平台值略高,与平均谱更接近。对于短周期段,本文对第一拐点进行了部分调整,既满足了T=0时的动力不放大规律,又使上升段与反应谱更贴合。本文的第一下降段的下降速度略高,第二下降段位置靠后,介于规范谱与平均谱之间。既保证了长周期位移控制段的安全性,又使其便于达到设计施工时的实际要求。 本文基于我国西南地区的强震动数据,通过场地划分和设计地震分组,利用基于全局和邻域变异的差分进化算法,对水平向抗震设计谱特征参数进行标定,分析了其随震级、震源距变化的规律以及与规范设计谱中特征参数的差异,给出了西南地区基于规范设计谱形式的特征参数建议取值。 由于采用了我国西南地区近年全部可用的水平向强震动数据,与基于单次地震的统计结果相比,本文结果全部基于区域性地震记录,更多地揭示了西南地区的地震动特征。 通过GLDE算法对设计谱特征参数T0、Tg、Td、βmax与γ进行高效标定,参数的变化规律表明:随着震级和震源距的增加,T0、Tg与βmax逐渐增大,Td与γ逐渐减小。按照不同设计分组和场地条件进行分类研究,特征参数整体趋势在放大系数谱中体现为:平台段逐渐上升并向长周期移动,下降段的趋势则变得平缓。与规范谱相比,βmax与γ更大,T0差异较小,Ⅰ类场地的Tg更小,Ⅱ类、Ⅲ类场地的Tg更大,Td并非Tg固定的倍数,而是更趋向于长周期方向。 致谢:感谢中国地震局工程力学研究所国家强震动台网中心为本研究提供数据支持。2.2 GLDE算法的稳定性验证
3 西南地区设计谱特征参数分析
3.1 设计谱特征参数标定结果的组别分析




3.2 标定结果与规范谱特征参数的比较


3.3 针对西南地区的特征参数取值建议
4 结论
--западе Китая

