温度与应变率对聚羟基脂肪酸酯弹塑性力学行为的影响
李佳妮,齐正磐,胡 宁,朱建斌,杨艳静
(1.河北工业大学机械工程学院,天津 300401;2.北京卫星环境工程研究所,北京 100094)
0 引言
高分子材料的飞速发展给人们带来了极大的便利,但与此同时也导致了大量固体废弃物污染,因而近年来随着石油资源的日益枯竭和绿色环保理念的深入人心,可降解高分子材料的开发与综合利用日益受到广大研究者的重视[1]。聚羟基脂肪酸酯(Polyhydroxyalkanoate,PHA)是一种天然的高分子聚合物,具有良好的生物可降解性,优异的生物相容性,因此在生物可降解的包装材料、组织工程材料(骨组织、神经导管组织、心脏瓣膜组织及血管组织)等方面都有广阔的应用前景[2]。故而,为了充分理解PHA的力学性能及其生物兼容性;有效确保相关产品设计的稳定性、耐久性和可靠性;充分挖掘生物可降解高聚物的工程使用价值和前景,现阶段亟需对PHA的力学性能进行系统深入的研究,在明确其力学性能影响因素的基础上,寻找建立简洁而精确的本构模型,对其基本力学行为进行模拟预测。
现阶段,人们在相关方面已经开展了较多研究,并取得了较为可观的研究成果。总体而言,当前有关PHA的研究主要集中在制备获取单体及其复合材料、PHA相关各类材料性能表征测试、PHA材料及产品的生物可降解和兼容性等方面。
关于PHA单体及其复合材料制备,大量研究旨在根据实际应用需求通过各类化学和工业方法实现可变基团置换、主体链长增减以及聚合度调控等。PHA是微生物体内的一类3-羟基脂肪酸组成的线性聚酯类高分子聚合物。其中侧链R作为可变基团,是区别不同PHA单体的核心依据;主链单体链长m可取值为1、2或者3;聚合度n一般在数百至数千之间。例如,当m为1,侧链R为甲基时,即为最常见的聚3-羟基丁酸(P3HB),也是目前研究最成熟的PHA之一。其中最具代表性的研究当属Narayanan从污染湖土中筛选出蜡样芽孢杆菌NDRMN001,在廉价营养因子作用下,该菌在短时间内能生产出优质的P3HB[3]。PHA的结构变化多样,不仅侧链的R和主链单体链长m均可变化,而且不同的单体还可以形成不同的共聚物,此外单体在共聚物中比例的变化也能导致共聚物的性能产生多种变化。例如,Melendez-Rodriguez通过混合微生物培养(MMC)技术获得了一种新的三元聚酯类聚合物,3-羟基丁酸-co-3-羟基戊酸酯-co-3-羟基己酸酯,简记为P(3HB-co-3HV-co-3HHx),该三元聚酯含有摩尔质量分数约68%的3-羟基丁酸盐(3HB),摩尔质量分数约17%的3-羟基戊酸盐(3HV)和摩尔质量分数15%的3-羟基己酸酯(3HHx)。P(3HB-co-3HV-co-3HHx)的弹性模量约为700 MPa,拉伸强度约为5 MPa,断裂伸长率高于4%,该三元共聚物中的3HHx分数越高,弹性模量越大[4]。由此可见,通常人们所说的PHA指的是一大类聚合物,它们种类多样、彼此之间链长差别非常大,因而不同种类的PHA材料属性差异也较大,某些表现出明显的脆性,而其他一些则具有较好的韧性[5-8]。
PHA及其复合材料性能表征测试的相关研究中,力学性能研究数量较多,但是由于PHA类材料种类繁多,力学性能受温度和加载速率影响较大,导致这类研究仅停留在性能表征测试方面,缺少变形机理探究、变形规律讨论抑或数值模拟计算。例如:Yves-Marie Corre 选取了Enmat Y1000P(P3HB-3HV)、Mirel F1006(P3HB-4HB)、Mirel F3002(P3HB-4HB)、P226(P3HB) 4种不同等级的商用PHA,通过拉伸试验获得的应力应变曲线,发现4 种PHA 的断裂伸长率都十分有限。Y1000P 晶体含量最高,是一类易碎的材料,P226断裂伸长率最高,作者将其归因于增塑剂的影响[9]。为满足应用需求,研究者们还通过制备复合材料以改善PHA的力学性能并进行测试。例如,Wu等[10]制备了板栗壳纤维(CSF)增强PHA复合材料以及CSF 和甲基丙烯酸缩水甘油酯接枝PHA(PHA-g-GMA)复合材料,并通过拉伸试验比较了二者的力学性能。由于CSF 中的羟基基团与PHA-g-GMA 中的甲基丙烯酸缩水甘油酯基团发生了缩合反应,使得CSF 与PHA-g-GMA 基体之间具有更好的粘附性,从而能有效提高PHA/CSF 复合材料的抗拉强度,但与此同时也降低了材料的断裂伸长率。又如,Ye等[11]制备了用于3D打印的β-磷酸三钙(β-TCP)增强聚羟基烷酸酯复合材料,经相关力学性能测试,发现随β-TCP含量的增加,PHA/β-TCP复合材料的强度极限和屈服应力均先增大后减小,且在β-TCP含量为20%时,均达到最大值,与基体PHA材料相比,该复合材料的强度极限提高了38.35%,屈服应力提高了20.18%。作者进一步指出当β-TCP含量少时,β-TCP能够更加均匀地分散在PHA 基体中,从而与PHA 分子链紧密结合,此时PHA/β-TCP 复合材料若受到拉伸作用力,β-TCP 与PHA分子链纠缠形成的物理结合点能够有效抑制PHA分子链的滑动,从而提高复合材料的拉伸强度极限;而当β-TCP含量较多时,β-TCP在PHA/β-TCP复合材料中的分散性较差,会在PHA基体中形成较大的团聚体,导致β-TCP与PHA基体之间的结合力下降,从而在外力作用下发生脱黏,使得复合材料的拉伸强度极限有所降低[11]。Chan等[12]制备了质量分数50%的木粉增强PHBV和P3HB4HB共聚物的复合材料并进行相关力学性能测试。研究发现,与纯PHBV相比,加入P3HB4HB能有效地改善共聚复合物的断裂应变,这主要是因为在没有共结晶的情形下,4-HB单元作为缺陷能明显扰乱P(3-HB)晶格的填充,从而导致较低的熔点,较低的结晶度以及较高的断裂应变;并且基体性能对复合材料的力学性能影响有限,此时PHA复合材料的力学性能反而主要由刚性和脆性的木粉所决定。综上所述,虽然针对各种PHA的力学性能存在为数众多的研究,但是这些研究主要是通过多种测试方法从实验的角度对材料的模量、强度和韧性等力学性能参量进行表征测试,并没有系统研究这些参量受拉伸速率,温度等因素的影响规律,也没有深入理解变形机理、应力应变关系、损伤起始演化等,对于材料本构模型和数值模拟的研究有待更进一步的探索。
从力学模拟的角度而言,PHA可以认为是一类新型的聚合物复合材料,故而聚合物力学与复合材料力学性能模拟的相关方法可以作为借鉴。这其中有限单元法及其衍生方法是研究各类材料力学性能的一类重要方法。但要进行有限元模拟,必须获得材料的本构模型。目前国内外文献并未阐述专门针对PHA的本构模型。究其原因在于,首先即使在室温条件下不同种类的PHA由于分子结构差异巨大导致本构行为差异较大,或表现为弹性,或表现为弹塑性,所以构建本构模型时必须指明具体的PHA种类和牌号;其次,高分子聚合物的本构行为还具有时间效应,或表现为黏弹性,或表现为黏塑性,甚至黏弹塑性,使得PHA本构模型的构建难度较大。目前,较为可行的方法是借鉴金属在高温条件下的本构模型,因为高温条件下金属也呈现出相关塑性甚至黏塑性行为[13]。这类本构模型一般可分为3 类[14],分别是基于“唯象学”本构模型[13,15-16]、基于物理机理的本构模型[17]和基于人工神经网络的本构模型[18-19]。“唯象学”本构模型是采用一定的原件组合和简单的数学方程组合来定量刻画材料的宏观应力应变关系;基于物理机理的本构模型是从热力学、能量守恒等基础理论出发并在一定程度上考虑材料内部微观结构变形机制的自洽理论模型;人工神经网络则是基于数据分析和集合映射的纯数学关系,提供了一种新的模拟材料变形行为的建模方法[20]。
3种类型中,“唯象学”本构模型因具有材料参数少、计算量小、更易校准等优点,从而得到广泛的应用。典型的唯象型本构模型有Johnson-Cook(J-C)模型[21]、Arrhenius模型[22]、Khan-Huang(KH)[23]等。其中J-C模型最初是为了描述金属在大变形、高应变速率和高温下的变形行为而提出的经验型本构模型,其流动应力是温度、应变率和塑性应变的函数[24],随后被广泛用于模拟多种金属的本构行为。例如,Bisht等[25]利用Johnson-Cook本构模型模拟了AM30镁合金在热加工过程中的变形行为。Jia等[26]建立了7A52铝合金的Johnson-Cook本构模型模拟该合金在一定温度与应变率下的准静态和动态拉伸试验,模拟结果与试验结果吻合较好。Gupta等[27]建立了Johnson-Cook模型来预测高磷钢的热变形行为。然而,原始的J-C模型只将材料的力学行为看作是应变、应变速率和温度的倍增效应,忽略了应变、温度和应变率之间的耦合效应。往往不能准确预测高温软化和加工硬化等对材料流动应力的影响。因此许多研究者对J-C模型加以修正。例如,Shokry[28-29]提出一种综合考虑了应变、应变速率和温度之间的耦合效应的Johnson-cook改进模型,用于精确预测各种常见合金的流动特性。并分别采用Johnson-Cook模型、改进的Johnson-Cook模型表征了纳米准晶Al93Fe3Cr2Ti2合金在不同应变速率和高温下的流动行为,结果表明改进后的Johnson-Cook 模型在测试范围内,预测应力数据与实验应力数据吻合更好。Chao等[30]提出了一种考虑应变软化的改进Johnson-Cook模型,该模型能更准确地估计体积分数分别为25%和55%B4C/2024Al复合材料的流动应力。Xu等[31]考虑温度与应变率之间的耦合关系改进了Johnson-Cook本构模型用于模拟SnSbCu合金在压缩载荷作用下的应力应变关系。
基于物理机理的本构模型和基于人工神经网络的本构模型虽没有“唯象学”本构模型应用广泛,但是都有各自的优点。物理模型[17]虽然较为复杂,材料参数难以确定,但是它们能够对高温和高应变率下材料宏观变形行为所蕴含的内在机制以及材料内部微观结构变化进行物理学和热力学解释,这是“唯象学”模型无法企及的。例如,Zhou等[32]考虑了P91钢的析出相硬化和分级晶界强化并结合基于物理的统一循环黏塑性本构模型,成功地预测了P91钢的循环软化。基于人工神经网络的本构模型通过应用许多称为神经元的非线性处理单元来模拟复杂的非线性关系。通过实验数据的适当训练,人工神经网络可以来“学习”这种关系并归纳其中的数学逻辑规律[33]。例如,Ling等[20]利用人工神经网络提出了高铌含量的β-γTiAl合金的高温本构模型,该模型的精度高于Arrhenius模型。
综上所述,近些年有大量的研究人员对多种材料的本构模型进行研究并取得了丰硕的研究成果。其中,“唯象学”本构模型参数较少且可在有限的应变率和温度范围内可取得较高精度,基于物理机理的本构模型和基于人工神经网络的本构模型虽然具有较多参数,但可以在较大的应变率和温度范围内进行模拟。然而这些研究主要是针对金属、陶瓷以及通用高分子材料的,对于PHA的本构模型还少有涉及。如前文所述有限元模拟是研究材料力学性能的一种重要方法,且只有将材料的本构模型融入有限元方法才能真实反映该材料在不同加载条件下的力学响应特性。因此,亟需对PHA的本构关系开展深入研究并对其力学行为进行精确模拟。
为系统深入研究不同类型PHA的宏观力学行为并揭示温度、应变率对PHA力学行为的影响规律,进而获得精确的本构模型,首先针对2种批号的PHA材料开展不同温度下和不同应变率下的宏观拉伸力学性能测试,并对测试数据进行分析归纳了温度和应变率对不同PHA力学性能的影响规律,继而借助扫描电镜和差示扫描量热仪(DSC)分别研究了不同PHA的变形破坏机理并揭示了造成不同PHA力学性能差异的根本原因,并分别借助线弹性本构模型和J-C本构模型实现了不同PHA的本构行为模拟。为便于阐述,下文将以产品编号指代具体材料。
1 PHA 的制备与实验
1.1 实验材料
作为生物可降解材料,PHA应用范围较广,为此选取了市面上销售量较大的2类最具代表性的PHA粒料EM10080和EM20010,前者属于食品级PHA,可作为食用产品薄膜和包装,后者属于注塑级PHA,可用于生产医疗器械。
1.2 实验仪器及设备
因PHA 粒料吸水率较高且性能受温度影响较大,加工前需在室温条件下进行真空干燥处理,故选用DZF-6020 真空干燥箱,其温控范围为10~200 ℃,温度波动为±1 ℃,真空度<133 MPa。根据粒料级别需求和测试件尺寸要求,选用武汉瑞鸣SZS-15微型注塑机制备测试件,该注塑机最大注射压力为45 MPa,最大合模力为120 kN,最大注射质量15 g。为进行拉伸测试,采用美特斯CMT5205电子万能试验机,最大力值为200 kN,分辨力为1/300 000 FS,即2/3 N,满足测试需求,力值相对误差为0.5%,行程800 mm,位移分辨力0.008 mm,位移相对误差为0.5%。为观测表针试样拉伸前后表面形貌,采用TESCAN MIRA LMS 扫描电子显微镜,加速电压200 V~30 kV,探针束流1 pA~100 nA,最大放大倍数100 000倍,分辨率0.9 nm。为获取材料的玻璃化转变温度,采用美国TA公司差示扫描量热仪,温度范围-80~500 ℃。

表1 实验材料Tab.1 Testing materials

表2 实验仪器及设备Tab.2 Testing instruments and equipment
1.3 试样的制备
将PHA粒料放入真空干燥箱干燥8 h后取出,用微型注射机注塑成符合ISO527-2改型的拉伸试样,试样制备成型后置于真空密封袋中保存。之所以选用ISO527-2改型,是综合考虑材料受力均匀性和万能试验机测试空间与量程的结果。试样的示意图如图1所示。

图1 试样尺寸示意图Fig.1 Diagram of specimen geometry
1.4 性能测试
1.4.1 力学性能测试
为了系统全面的研究不同种类PHA的力学性能以及应变率和温度对PHA力学行为的影响,特意选取了两种具有代表性的PHA,并分别在4种不同的加载速率(分别为0.004 mm/s、0.020 mm/s、0.100 mm/s 和0.500 mm/s)和2 种不同温度(分别为22 ℃和62 ℃)下进行了准静态单轴拉伸测试。考虑到测试数据的离散性和统计学规律,每组测试重复3次,其中编号为EM20010的PHA在62 ℃下的实验,因同批次试样不足仅完成了部分测试。需说明的是PHA的注塑成型条件极为苛刻,且注塑工艺对最终成型样件的力学性能影响较大,所以不同批次的试样力学测试结果的分散性可能较大,不利于规律研究和机理揭示,故而在能够确定影响规律的情况下未再补做测试。具体实验要求如表3所示。

表3 力学性能测试方案Tab.3 Testing plan for mechanical properties
1.4.2 形貌观察
将制备的PHA标准试验件(拉伸件与原件)浸泡于液氮中数分钟并将样条脆断成约4 mm×4 mm×3 mm的块状。使用Oxford Quorum SC7620 溅射镀膜仪对表面喷金60 s。随后使用TESCAN MIRA LMS扫描电子显微镜拍摄样品表面形貌,形貌拍摄时加速电压为3 kV,探测器为SE2二次电子探测器。
1.4.3 热力学分析
因产品EM20010 在22 ℃和62 ℃时力学性能差异较大,故用差示扫描量热仪(DSC)对EM20010进行测试分析从而获取其玻璃化转变温度。首先取任一试样,从中切取约5 mg的材料块体,置于DSC测试腔体内。表征测试过程中,以高纯氮气作为保护气体,起始平衡温度为30 ℃;以10 ℃/min的速率升温至170 ℃;无需保温;随即以10 ℃/min的速率降温到0 ℃以消除热历史;然后再以10 ℃/min的速率升温至170 ℃。记录最后一次升温过程中的热谱图。
2 实验结果
2.1 PHA 的力学性能
为了清晰呈现测试条件对材料力学性能的影响效果,对于同一测试条件下不同试样的测试结果进行了离散插值,然后在各离散点求平均值的方法获得了平均测试结果曲线。图2 为EM10080 在22 ℃时不同拉伸速率的工程应力-应变曲线。从图2 可知,常温下EM10080呈现出明显的屈服特征;且屈服后应力应变曲线呈现一定程度的下降(即应变软化现象),这是聚合物大分子在外力作用下的旋转重排所导致;随后聚合物分子链在拉伸方向的微小伸长导致材料表现出微弱的强化现象(即应力应变曲线略微上升);而试样最终断裂都表现为瞬断,并没有呈现出类似于金属材料柔性断裂的下降阶段。此外,随着加载速率的增加(等效于应变率增加),材料屈服应力增加较为明显,然而最终断裂应力以及延伸率的规律性并不明显,这是因为屈服应力是试样整体平均力学性能,而最终断裂与试样局部微观缺陷密切相关。值得注意的是22 ℃时不同拉伸速率下的曲线在工程应变2.25 左右相交,这一有趣现象背后的机理正在进一步探索研究中。

图2 22 ℃下EM10080 不同拉伸速率的工程应力应变曲线Fig.2 Engineering stress-strain curves of EM10080 at different tensile speeds at 22°C
图3 为EM10080 在62 ℃时不同拉伸速率下的工程应力-应变曲线。从图3 可知,EM10080 在高温下的应力应变趋势与室温下相似,经历了初始弹性阶段后即发生明显屈服,屈服应力随着温度的升高而降低。高加载速率下屈服之后会出现微弱的应变软化阶段,而当加载速率为0.004 mm/s时,软化现象消失。
图4 进一步对比了22 ℃和62 ℃时EM10080 应力应变曲线的异同。显然,随着温度的升高,EM10080的杨氏模量和屈服应力都显著降低,原因在于高温下材料大分子链流动性增强,从而导致克服分子间作用力所需的外力有所降低。

图4 相同加载速率不同温度下EM10080 的工程应力应变曲线Fig.4 The engineering stress-strain curves of EM10080 at the same loading rate and different temperatures
图5 对比了EM10080试样测试前后形貌,无论室温下还是高温下,试样都呈现了典型的颈缩现象,并且具有明显的延展性。由于高温下,材料的延展性增强,所以高温下部分试样在测试结束时并没有被拉断,即使此时试验机已经达到了其最大行程。
图6 给出了室温下EM10080 的屈服应力与杨氏模量随加载速率的变化趋势。图7 展示了高温62 ℃时EM10080的屈服应力与杨氏模量随加载速率的变换趋势。根据图6和图7可知,无论室温还是高温,随着加载速率的增大,EM10080的屈服应力和杨氏模量均显著增加。因为外力作用下,高分子材料的变形是依靠大分子链的蠕动来实现的,对于线性分子链而言,通过蠕动达到热力学平衡状态需要一定的时间,所以高加载速率下,外力作用迅速传递到试件中心,而变形则是通过分子链缓慢传递的,从而导致记录的应力数据较大而应变数据较小,呈现出了较大屈服应力和较大杨氏模量。

图6 25 ℃下EM10080 的屈服应力与杨氏模量随加载速率的变换趋势图Fig.6 Trend diagram of yield stress and Young′s modulus of EM10080 with loading rate at 25 ℃

图7 62 ℃下EM10080 的屈服应力与杨氏模量随加载速率的变换趋势图Fig.7 Trend diagram of yield stress and Young′s modulus of EM10080 with loading rate at 62 ℃
图8 为EM20010 在22 ℃时不同拉伸速率下的工程应力-应变曲线。室温下EM20010 呈现明显的线弹性变形行为。而且加载速率越大,抗拉强度也越大,因为当加载速率提高时,大分子链蠕动远远滞后于外力作用传递,因此链段发生断裂时所施加的外力更大,材料的抗拉强度也随之更大。

图8 22 ℃下EM20010 不同拉伸速率的工程应力应变曲线Fig.8 Engineering stress-strain curves of EM20010 at different tensile rates at 22°C
图9 为62 ℃时EM20010 在不同拉伸速率下的工程应力-应变曲线。与室温不同,高温下EM20010 呈现明显的塑性变形。当加载速率较大时,曲线首先表现为线弹性,然后依次是屈服、应变软化,最后表现为硬化。而随着加载速率的降低,材料的初始模量显著下降,屈服峰和应变软化也逐渐消失,但是非线性强化现象依然存在。外力作用下,聚合物分子链吸收足够能量后会沿着外力方向重新排列,当加载速率较大时,聚合物基本处于绝热状态,聚合物在外力做功下,试样温度升高而产生热变形,进而导致应变变化较大,当热变形占主导地位时,这反映在应力应变曲线上就是应变软化阶段。随着应变的增加,分子链的取向程度也随之增加,但是由于变形时间有限,分子链没有足够的时间来解取向,即分子链的取向排列占主导地位,因此,曲线最后表现为强化。当加载速率较低,变形时间延长时,分子链在取向排列的同时也在解取向,应力应变曲线表现的应变硬化程度就会比高加载速率小。

图9 62 ℃下EM20010 不同拉伸速率的工程应力应变曲线Fig.9 Engineering stress-strain curves of EM20010 at different tensile rates at 62°C
图10 是拉伸后的试样形貌前后对比,显然室温下EM20010 发生脆性断裂,而高温下材料发生柔性断裂。对比图9、图10可以看出,EM20010在22 ℃下呈现出线弹性变形行为以及脆性损伤断裂,然而在62 ℃下则表现为弹塑性变形行为和柔性损伤断裂。动力学理论认为,聚合物从高温下出现塑性到低温下出现脆性的转变是由于形成了聚合物构象重排。主链上单键旋转时会产生能量势垒。当温度高于玻璃化转变温度时,分子运动有足够的能量去克服能量势垒已到达平衡;相反,当温度低于玻璃化转变温度时,分子热运动的能量势垒难以克服,分子运动发生冻结。为了进一步求证,针对EM20010 做差示扫描量热仪(DSC)进行热力学分析,获取了EM20010的玻璃化转变温度,DSC测试结果将在2.3详细说明。
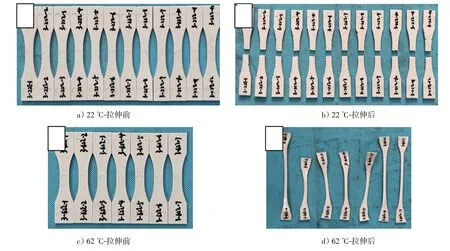
图10 EM20010 拉伸前后形貌对比Fig.10 Morphology comparison of EM20010 before and after stretching
2.2 PHA 的表面形貌分析
图11 为通过扫描电镜观测而得的EM10080原件、22 ℃拉断后样件以及62 ℃下拉断后样件表面微观形貌。显然,无论室温还是高温下,拉断后样件表面都出现了平行于拉伸方向的微观裂纹,使得材料表面呈现出类似于被“撕裂”形貌,因为塑性阶段材料的大分子链沿着拉伸方向重排伸长,导致垂直于拉伸方向逐渐收缩,使得不同部位之间出现了梭形“撕裂”孔。

图11 EM10080 的SEM 图Fig.11 SEM image of EM10080
图12 为通过扫描电镜观测而得的EM20010原件、22 ℃拉伸后样件以及62 ℃下拉伸后样件表面微观形貌。和EM10080相比,受试样制备工艺影响,试样表面光更为光滑平整。22 ℃下,EM20010的“撕裂”孔形状更趋近于条状,是因为该温度下,EM20010表现出脆性特点,断裂延伸率小,试样拉断时分子链沿着拉伸方向的伸长量就小,那么垂直于拉伸方向的收缩量也相应较小,“撕裂”孔形状较小,表现为条状。62 ℃下,试样伸长过大,已经超出引伸计量程但并未被拉断,为了确保应变数据的准确性,故而摘掉引伸计后也未继续进行测试,所以图12c)对应的是图10d)中未拉断试样的表面形貌,因此并未出现撕裂孔。

图12 EM20010 的SEM 图Fig.12 SEM image of EM20010
2.3 PHA 的热力学分析
EM20010 的DSC 曲线如图13 所示,从材料的二次升温曲线可得到EM20010 的玻璃化转变温度为55.96 ℃,由此可见在62 ℃下EM20010的应力应变曲线之所以表现出塑性,正是因为此时的测试温度已经跨过了该材料的玻璃化转化温度。
3 本构模型参数计算
根据实验结果,PHA的力学性能与温度和拉伸速度密切有关,在众多温度和率相关的本构模型中,基于“唯象学”的和基于微观结构的物理机理的两类本构模型各有优劣,前者适用于工程应用,参数较少易于标定且能够保证较高的计算精度,后者考虑了了材料内部微观结构和塑性变形机理,但是数值实现较为困难。其中,Johnson-Cook模型是应用最为广泛且待定参数较少,并在众多场合中被验证了模拟精度的一种“唯象学”本构模型。因此采用Johnson-Cook本构模型模拟EM10080的温度与率相关应力应变响应;而且根据测试结果初步判断模型中的幂次强化项能够反映材料的强化行为,因为当幂指数小于1 时曲线上凸,当幂指数大于1时曲线下凸;对数线性项也能够反映应变率对初始屈服应力的影响。这些推测也被模拟结果所证明,详见下述章节。
3.1 Johnson-Cook 本构模型
Johnson-Cook本构方程的公式如下:
式中:σeq为等效应力;εeq为等效塑性应变;为等效应变率;为参考应变率;T*=(T-Tr)/(Tm-Tr),T为当前温度,Tr为参考温度,Tm为材料熔点温度,这里取438 K[34];A、B、C、n、m为模型参数。公式第1 项表示参考温度、参考应变率条件下材料的流动应力与应变的关系;第2项反映的应变率对流动应力的影响,在参考应变率时,该项为1;第3 项反映的是流动应力随温度变化的关系,在参考温度时该项为1。本文将根据实验条件下的应力应变关系拟合得到式(1)中的A、B、n、m和C参数,其中设定拉伸速率为0.004 mm/s,即应变率为0.000 067 s-1时为参考应变率。
首先,将22 ℃即295 K下的工程应力应变曲线,转化为真实应力应变曲线如图14。

图14 295 K 下EM10080 真实应力应变曲线Fig.14 The true stress-strain curve of EM10080 at 295 K
在屈服点处,295 K时不同应变率下,εeq=0,所以,设,此时式(1)化为
展开得
选拉伸速率为0.004 mm/s,0.020 mm/s两曲线代入屈服点处数据,数据如表4所示。解得:

表4 代入数据Tab.4 Substituting data
用同样的方法将0.004 mm/s,0.500 mm/s 两曲线代入屈服点处数据解得C=0.04 ,求平均值取C=0.02。在参考应变率下,此时式(1)化为
采用式(6)对295 K,参考应变率下屈服后的真实应力应变数据进行曲线拟合,如图15所示。拟合得:

图15 参数拟合Fig.15 Parameter fitting
在参考应变率,屈服点处,此时式(1)化为
等式两边同时除以A并移项得
对该式两端取对数得
代入295 K、335 K温度下的屈服应力求解,代入数据如表5所示。解得:

表5 代入数据Tab.5 Substituting data
由此获得产品编号为EM10080 的PHA 全部Johnson-Cook本构模型参数如表6所示。

表6 Johnson-Cook 本构模型参数Tab.6 Parameters of Johnson-Cook constitutive model
3.2 线弹性本构模型
EM20010在22 ℃时表现出线弹性变形行为和脆性断裂,因此采用线弹性本构模型,只需要输入弹性模量和泊松比2个参数如表7所示,其中泊松比取值参考Bejagam的研究[35]。EM20010在62 ℃时表现为弹塑性变形行为和延性断裂,用传统弹塑性本构模型进行模拟。

表7 线弹性本构模型参数Tab.7 Parameters of linear elastic constitutive model
4 模型验证
4.1 EM10080 本构模型验证
如图16所示,在有限元软件中建立PHA 拉伸模型,根据实验得出的应力应变曲线,计算得出该PHA的弹性模量为48.88 MPa,泊松比取为0.4[35]。将上文所求J-C本构模型参数输入有限元软件。试样左端采取固定约束,右端施加水平向右的速度载荷,在预定义场变量中分别施加温度为295 K与335 K。采用显示动力学分析步进行计算。模拟所得的应力应变曲线与测试结果比较如图17、图18所示。

图16 单轴拉伸测试有限元模拟示意图Fig.16 Simulation based on FEM of uniaxial tension

图17 不同温度相同拉伸速率下EM10080 模拟与实验曲线Fig.17 EM10080 simulation and experimental curves at different temperatures and the same tensile rate
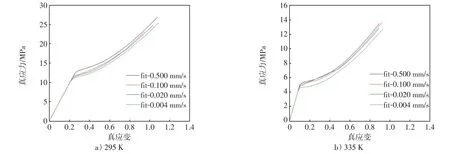
图18 不同拉伸速率下EM10080 模拟曲线Fig.18 Simulated stress-strain curves of EM10080 at various loading rates
图17给出了EM10080拉伸试验与模拟的应力-应变曲线比较结果,其中图17a)为参考应变率下的测试曲线与模拟曲线。图17表明Johnson-Cook本构模型能够模拟EM10080的力学行为,并且本构模型中的参数A、B和n的取值较为合理;同时,本构模型也能够有效刻画温度对材料应力应变曲线的影响,进而说明本构模型中参数m的取值较为合理。
图18中将不同应变率下的模拟结果绘制在同一坐标系中,显然,Johnson-Cook本构模型能够反映应变率对材料应力应变曲线的影响,也说明参数C的取值合理。
4.2 EM20010 本构模型验证
由于EM20010 在22 ℃时表现为线弹性变形,故采用线弹性本构模型对其力学行为进行模拟。并且此时材料的变形行为不依赖于应变率,因此只需给出22 ℃下0.004 mm/s加载时的模拟结果与测试结果,即可说明材料的变形特征以及模拟精度,如图19 所示,显然线弹性本构能够有效刻画材料的线弹性变形行为。当温度升高至62 ℃时,EM20010 表现出显著的弹塑性变形,此时则需采用传统弹塑性本构模型对其应力应变曲线进行模拟,结果如图20所示。

图19 295 K 下EM20010 模拟与试验曲线Fig.19 Simulation and experimental curves of EM20010 at 295 K

图20 335 K 下EM20010 模拟与试验曲线Fig.20 Simulation and experimental curves of EM20010 at 335 K
5 结语
针对2种常见的PHA材料(牌号分别为EM10080和EM20010)开展不同应变率和不同温度下的轴向单拉测试、界面微观形貌表征测试以及DSC 测试,进而根据测试结果采用合适的本构模型分别对2 种牌号PHA的应力应变响应进行了精确模拟,获得了以下结论。
1)2种牌号的PHA材料的力学行为都表现出了显著的温度相关性和应变率相关性,并且屈服应力和杨氏模量等力学性能均随应变率的升高而升高,但是随着温度的升高而降低。
2)温度和应变率不仅影响材料的力学性能,也影响材料的应力应变曲线形态。对于EM10080 而言,较高应变率下和较低温度下,屈服后的软化现象更为明显。对于EM20010而言,22 ℃时曲线表现出明显的线弹性特征,类似于脆性玻璃;而62 ℃时曲线表现出显著的弹塑性特征,类似于热塑性橡胶,这是因为EM20010的玻璃态转化温度为55.96 ℃。
3)准静态拉伸过程中,由于大分子链沿着拉伸方向重排,所以2种牌号PHA 试样表面均出现平行于拉伸方向的裂纹,使得试样呈现出类似于被“撕裂”的状态。其中EM10080 的裂纹近似于“梭形”,而EM20010的裂纹近似于“条状”。
4)Johnson-Cook本构模型能够精确模拟EM10080在不同温度和不同应变率下的应力应变响应。但是由于EM20010的力学行为更为复杂,因此目前采用线弹性本构模型模拟常温下应力应变响应,而采用传统弹塑性本构模型模拟高温下应力应变响应,后续需要更深入研究来建立考虑温度的普适型本构模型。

