基于Kriging模型的双变量降维方法

韩忠皓，张德权，杨美德，赵海文

（1.河北工业大学机械工程学院，天津 300401；2.湖南大学机械与运载工程学院，湖南 长沙 410082）

0 引言

功能函数的统计矩是机械系统进行可靠性分析的前提和基础，其计算效率决定着机械系统可靠性分析的效率。随着机械系统愈加复杂，高效地获得功能函数统计矩变得愈加重要，已成为近年来的研究热点。

当前，功能函数统计矩的计算方法主要包括三点估计方法[1-2]、稀疏网格法[3]和降维法[4-6]等。对于三点估计方法，Seo等[1]提出对于n维不确定变量问题，需要调用3n次功能函数。相关研究表明[7]：当涉及到高维问题时，三点估计方法的功能函数调用次数会随着不确定变量个数的增加呈指数增长，其计算效率非常低。针对三点估计方法的缺点，Smolyak[3]提出一种稀疏网格法，该方法具有较高的计算精度，有效地解决了高维和变量强相关的不确定分析问题，但仍需调用大量的功能函数。Rahman等[5]提出了降维方法，其主要包括单变量降维法[5-6]和双变量降维法[4]，单变量降维法将一个多维问题转换为多个一维问题进行分析，具有较高的计算效率，但该方法忽略了二维及以上积分的残差，在遭遇强非线性问题时获得的高阶统计矩误差较大。相比而言，双变量降维法在计算精度方面比单变量降维法更具有优势，但由于需要调用更多的功能函数导致其计算效率较低。

此外，考虑到代理模型[8-9]可以在保证近似精度的基础上大大提高计算效率，一些研究者将代理模型应用于功能函数的统计矩计算中应对复杂问题，这类方法可以显著改善计算效率，但其精度取决于样本点的选取和模型参数的选取。常见的代理模型有Kriging模型[9-10]、径向基模型[8，11]、支持向量机模型[12]、响应面模型[13]、人工神经网络模型[14]、混沌多项式展开模型[15]等，其中Kriging 模型因其可以预测局部方差的优点而备受关注。Won等[16]将Kriging模型与单变量降维方法相结合，提出了基于Kriging的单变量降维方法。尽管该方法改善了单变量降维方法的计算效率，但并没有提高单变量降维方法的计算精度。范文亮等[17]将Kriging模型与双变量降维方法相结合，提出了基于双变量降维和Kriging近似的统计矩评估方法，该方法采用“米”字型节点构建功能函数的Kriging模型，与原双变量降维方法相比，显著提高了统计矩计算效率，但该方法仅仅是简单的使用Kriging模型代替真实功能函数。对于一般工程问题来说，该方法构建的Kriging模型精度是足够的，但对于复杂工程问题来说，无法判断“米”字型节点构建的Kriging模型是否准确，可能导致获得不精确甚至错误的统计矩结果。

鉴于此，本文将U学习函数和Kriging模型引入到双变量降维方法中，提出了一种新的基于Kriging模型的双变量降维方法。不同于仅仅采用“米”字型节点构建功能函数的Kriging模型，提出的方法在使用Kriging模型代替真实的功能函数的基础上，进一步采用U学习函数逐步地挑选对响应函数值影响最大的高斯积分点，减少使用对计算精度影响较小的积分点。此外，通过采用停止准则，提出的方法能够在保证精度的前提下，减少功能函数调用次数，有效克服传统双变量降维法计算效率低的问题。

1 双变量降维方法

为提高计算系统响应统计矩的精度，Xu 等[18]在单变量降维方法的基础上进一步提出了双变量降维方法。与单变量降维方法类似，双变量降维方法的实施包括3个步骤。

1）将一个多维响应函数等效为多个二维响应函数与多个一维响应函数的叠加，其数学形式如下：

式中：n表示随机变量的维数；g(·)表示系统响应的功能函数；和表示二维响应函数的第i1和i2个随机变量；xi表示一维响应函数的第i个随机变量；μi(i=1,…,n)表示随机变量的均值。

2） 根据所有二维响应函数与一维响应函数的统计矩近似计算多维响应函数的统计矩。令，根据矩的定义，其l阶近似响应函数原点矩可表示为

3）采用基于矩的求积法则[18]计算式（2）中的积分。

2 Kriging 模型和U 学习函数

2.1 Kriging 模型

Kriging模型由线性回归项和非参数项2部分组成[19]，具体表达式为

式中：θ为相关参数；Rθ(Xi,Xj)为两点的相关函数，其表达式为

式中：xi,q表示样本点Xi的第q个响应；θq为第q个相关参数。这些参数可以通过最大似然估计法[19]获得：

式中，R为对称相关矩阵，Rij=Rθ(Xi,Xj)，i,j=1,2,…,n。采用广义最小二乘法[19]计算回归系数β和σ2的估计值

式中：F是包含m1×m2个元素的矩阵，。

给定一个预测点X0，在该点预测的函数值和方差为

式中，u=FTR-1r0-f(X0)。在本研究中，采用DACE工具箱[20]建立Kriging模型并计算相应的预测值。

2.2 U 学习函数

在保证Kriging 模型具有足够精度的前提下，尽可能提高计算效率，Echard 等[21]提出了一种U 学习函数，并采用该学习函数寻找潜在最优样本点更新Kriging模型，逐步改善Kriging模型的精度。U学习函数[21]的数学表达式为

3 提出的方法

3.1 基于Gauss-Hermite 的统计矩评估

基于矩的求积法则在解决线性方程组时可能遭遇数值不稳定现象[22-23]，受Huang 等[4]研究工作的启发，本研究采用Gauss-Hermite数值积分求解式（2）以解决上述问题。

引入一个函数T将随机变量转变为服从正态分布U～N(0,1 2 )的正态变量。该T函数的数学形式如下：

式中：Ti表示随机变量xi的转变函数；Φ-1[·]为标准正态随机变量累积分布函数的逆函数；是随机变量xi的累积分布函数。

采用高斯埃尔米特积分[4]，式（14）可以表示为

式中：g(·)表示系统响应的功能函数；为第i1个变量关于第I1个积分点的高斯权重系数；为第i2个变量关于第I2个积分点的高斯权重系数；为第i1个变量关于第I1个积分点的高斯积分点；为第i2个变量关于第I2个积分点的高斯积分点；r，r1和r2均表示高斯积分点的个数。表1列出5阶高斯埃尔米特积分节点和相应的权重。当求解式（15）时，为了保证足够的精度，一般选择5阶高斯埃尔米特积分节点。

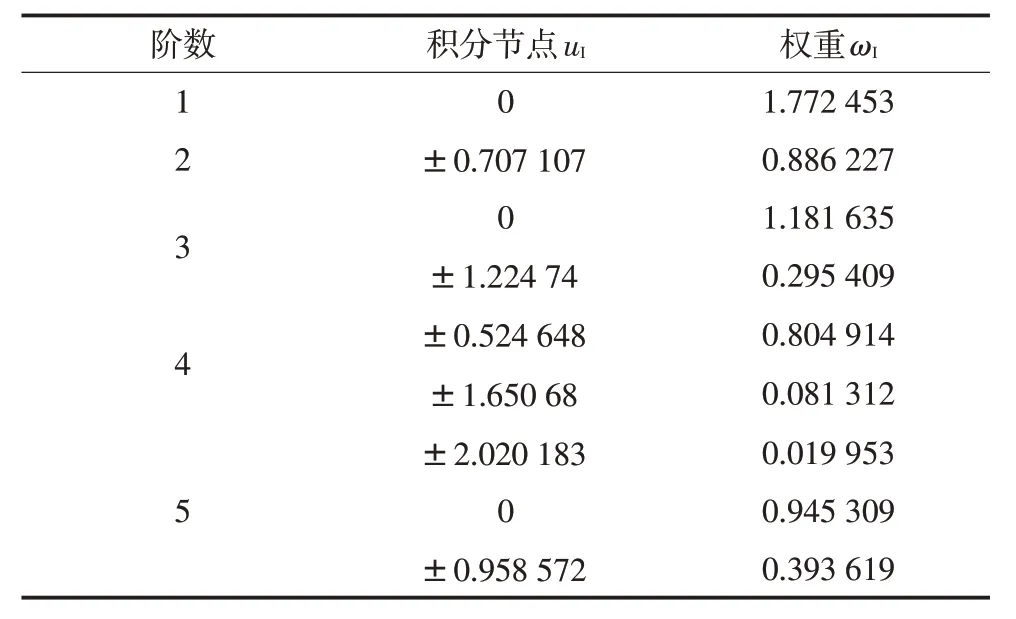
表1 高斯埃尔米特积分节点和权重[4]Tab.1 The nodes and weights of Gauss-Hermite integral

根据前4 阶统计矩与原点矩的关系[24]，统计矩可表示为

式中：m1，m2，m3和m4是前4 阶原点矩；D1，D2，D3和D4是前4阶统计矩。

3.2 基于Kriging 模型的积分节点选取策略与收敛准则

3.2.1 积分节点的选取策略

当采用5 阶高斯埃尔米特积分节点时，对于式（15）任意一个二维响应函数，需要调用52次功能函数；对于任意一个一维响应函数，需要调用5次功能函数。为了进一步减少功能函数调用次数，本研究采用Kriging模型代替真实功能函数，并引入U学习函数逐渐增加新的积分点更新Kriging模型。

1）构建一维响应函数的Kriging模型

选择坐标轴上距离原点最近的2个积分点作为初始样本点，采用U学习函数逐渐增加新的积分点更新Kriging模型，直到满足收敛准则。为了便于理解，图1给出一维响应函数Kriging 模型样本点的选取示意图。如图1 所示，黑色实心圆（）表示坐标原点，红色空心圆（）表示建立一维响应函数Kriging 模型的初始样本点，黄色实心圆（）表示建立单变量响应函数新增的样本点，绿色实心圆（）表示建立Kriging模型未使用的样本点。

与国外的机构库建设的高速发展相比，我国目前还处于起步阶段。吴建中[3]2004年初发表文章探讨了机构库对图书馆整体管理模式的冲击，将知识库的概念引入我国。2005年7月，北京大学图书馆率领国内50多所高等院校图书馆联合发表《图书馆合作与信息资源共享武汉宣言》，在宣言中明确指出我国高校图书馆应“建设特色馆藏，开展特色服务，建立一批特色学术机构库（Institutional Depository）”[4]。从那之后，机构知识库的建设在国内，特别是我国高校图书馆逐步开启[5]。

图1 一维响应函数Kriging 模型样本点的选取示意图Fig.1 Schematic diagram of sample points selection in Kriging model for one dimensional response functions

2）构建二维响应函数的Kriging模型

选择坐标轴上的9个积分点作为初始样本点（红色空心圆），采用U 学习函数逐渐增加新的积分点更新Kriging 模型，直到满足收敛准则。为了便于理解，图2给出二维响应函数Kriging模型样本点的选取示意图。如图2所示，红色空心圆（）表示建立二维响应函数Kriging 模型的初始样本点，黄色实心圆（）表示建立二维响应函数新增的样本点，绿色实心圆（）表示建立Kriging模型未使用的样本点。

图2 二维响应函数Kriging 模型样本点的选取示意图Fig.2 Schematic diagram of sample points selection in Kriging model for two dimensional response functions

3.2.2 停止准则

为了提高计算效率，当更新的一维响应函数和二维响应函数Kriging模型分别达到足够精度时，其Kriging模型则停止更新。为此，本文引入以下收敛准则[21]：

式中：δ表示功能函数值的误差；ε为允许的误差值；表示Z(·)的预测值；Range(Z(u))=max(Z(u))-min(Z(u))，其中u为已存在的样本点，u′为新加入的样本点。本文中，ε取值为0.000 1。

3.2.3 计算统计矩

通过构建一维响应函数和二维响应函数的Kriging模型，式（15）可进一步变换为

3.3 实施步骤和流程图

提出方法的实施步骤如表2所示，流程图如图3所示。

图3 提出方法的流程图Fig.3 Flowchart of the proposed method

表2 提出方法的实施步骤Tab.2 The implementation steps of the proposed method

4 算例验证

4.1 算例1

采用文献[5]中三维非线性功能函数验证提出方法的有效性，其表达式为

式中，随机变量x1，x2和x3是相互独立且均服从均值为0.918，标准差为0.210 的韦布尔分布，其边缘概率密度函数为。

将双变量降维方法、提出的方法与蒙特卡洛模拟方法计算得到的前4 阶统计矩进行对比如表3 所示，可以看出传统双变量降维方法和提出方法获得的前4阶矩结果基本一致，且都接近蒙特卡洛模拟计算结果，表明计算精度能够得到保证。在计算效率方面，提出方法调用功能函数次数比传统双变量降维方法少16次，从而提高了统计矩的计算效率。

表3 算例1 不同方法计算结果Tab.3 Computational results of different methods in example 1

4.2 算例2

考虑含5 个随机变量的非线性功能函数[23]，其表达式为

式中：随机变量相互独立且服从正态分布；均值分别为μ1=1.2，μ2=2.4，μ3=50，μ4=25和μ5=10；标准差分别为σ1=0.36，σ2=0.072，σ3=3，σ4=7.5和σ5=5。

双变量降维方法、提出的方法与蒙特卡洛模拟方法的计算精度和效率对比如表4 所示。从表4 可以看出，传统双变量降维方法和提出方法获得的前4 阶矩结果基本一致，且都接近蒙特卡洛模拟计算结果，再次证明提出方法具有较高的计算精度。在计算效率方面，提出方法功能函数调用次数约为传统双变量降维方法的一半，计算效率得到了显著提升。与算例1相比，算例2随机变量维数增多，提出方法在节省调用功能函数次数方面具有显著的效果。

表4 算例2 不同方法计算结果Tab.4 Computational results of different methods in example 2

4.3 算例3

SCARA机器人[25]有4个关节，其中3个旋转关节的轴线相互平行，在空间内进行定位和定向，1个移动关节用于实现末端件在垂直于水平面的运动。SCARA 机器人示意图和机构运动简图如图4a）和图4b）所示。表5列出了SCARA机器人的D-H参数[25]，其中L1=200，θ1=0和d3=250为确定值，其他不确定变量的信息如表6所示。

图4 SCARA 机器人示意图和机构运动简图Fig.4 Schematic diagram and mechanism motion diagram of the SCARA robot

表5 SCARA 机器人D-H 参数[25]Tab.5 D-H parameters of the SCARA robot

表6 SCARA 机器人不确定参数Tab.6 Uncertain parameters of the SCARA robot

将双变量降维方法、提出方法与蒙特卡洛模拟方法计算获得的前4 阶统计矩进行对比，表7、表8 和表9分别列出工业机器人末端位置X，Y和Z方向坐标统计矩的计算结果。

表7 不同方法计算SCARA 机器人X 方向统计矩Tab.7 The computational statistical moments by different methods in X direction for the SCARA robot

根据计算结果可以看出，提出的方法无论是在均值，标准差，偏度还是峰度，计算精度都与原双变量降维方法相近，且都接近蒙特卡洛模拟方法的计算结果。此外，与原双变量降维方法相比，提出方法在3个方向的功能函数调用次数都明显减少，Z方向功能函数调用次数减少了46次，X和Y方向功能函数调用次数约为原双变量降维方法的一半，证明提出方法在保证计算精度的前提下，实现统计矩的高效计算。

5 结论

本文将Kriging模型和U学习函数引入到双变量降维方法中，提出一种改进的双变量降维方法，与传统双变量降维方法和蒙特卡洛模拟法进行精度和效率的比较。两个数值算例和SCARA机器人算例的计算结果表明：提出的方法能够在保证计算精度的前提下，提高传统双变量降维方法的计算效率，减少功能函数的调用次数。此外，提出方法可应用于其他复杂机械装备的不确定性分析和可靠性优化设计。