基于空间投影的函数最佳平方逼近注记

倪 倩, 王旭辉

(1.南京工业大学 数理科学学院,南京 211816; 2.中国科学院 数学与系统科学研究院,北京 100190; 3. 河海大学 数学学院,南京 211100)

0 引 言

函数的最佳平方逼近是数值分析课程中的重要部分[1-2],该内容也与最小二乘法紧密相连,在后续的理论分析和实际应用中有着广泛的用途[3].在平时的课堂教学中,通常都是将函数的最佳平方逼近问题转换为最小二次问题进行讲解,实践表明,这样处理,学生不容易理解和掌握.因此,如何处理这部分内容,便于学生理解是教师值得研究的问题.本文尝试将向量空间投影理论[4]应用到函数最佳逼近,最小二乘法与微分方程Galerkin方法求解问题的讲解中,可使学生更加直观地理解相关内容,促进学生对相关内容的掌握和应用,并培养学生融会贯通处理学习内容的能力.

1 函数的最佳平方逼近简介

给定函数f(x)∈C[a,b]及函数空间Φ,其中Φ由基函数φ1(x),φ2(x),…,φn(x)张成,φi(x)∈C[a,b],i=1,2,…,n.函数f(x)在空间Φ中的最佳平方逼近问题为:计算φ∈Φ使得误差函数

(1)

达到最小,其中ω(x)为给定的权函数.

计算c1,c2,…,cn使得E(c1,c2,…,cn)达到最小,可求解下列线性方程组

(2)

上述方程组 (2) 可化简为

(3)

2 空间投影及函数最佳平方逼近

下面引入向量的空间投影.

2.1 向量的空间投影

给定向量u∈d,d∈+及d中的子空间V,其中V由基向量v1,v2,…,vn张成.记v为u在子空间V中的投影,即v∈V且

(4)

其中cT=(c1,c2,…,cn)∈n,A=(〈vi,vj〉)i,j=1,2,…,n,bT=(〈u,v1〉,〈u,v2〉,…,〈u,vn〉).又由于v1,v2,…,vn线性无关,故A非奇异.此外,由 (4) 式得,E1为关于变量c1,c2,…,cn的二次函数,其最小值在cT=(c1,c2,…,cn)满足Ac=b时取得.故u在V中的投影v可表示为

v=(v1,v2,…,vn)A-1b.

上述求解过程具有直观的几何解释(见图1示意图).

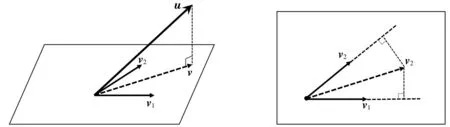
图1 向量投影示意图

特别地,当v1,v2,…,vn两两正交时,A=diag(〈v1,v1〉,〈v2,v2〉,…,〈vn,vn〉).此时,u在V中的投影可表示为

2.2 空间投影与函数最佳平方逼近

对于函数的最佳平方逼近问题 (1),可借助向量的空间投影进行处理.定义内积

用函数空间Φ代替3.1节中向量空间V,用函数空间Φ的基函数φ1(x),φ2(x),…,φn(x)代替3.1节中的向量空间V的基,从而对于函数的最佳平方逼近问题,从空间投影的角度可建立法方程组

特别地,当φ1(x),φ2(x),…,φn(x)为一组正交基,即φ1(x),φ2(x),…,φn(x)满足

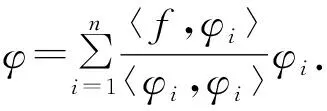
注1(最小二乘问题情形) 如果考虑最小二乘问题:给定点(xi,yi),权因子ωi,i=1,…,l,计算

注2(微分方程的Galerkin方法求解[5]) 如果考虑如下齐次微分方程求解问题:

(5)

可将向量空间中内积替换成能量内积 (Energy inner product)

针对微分方程问题 (5), 可通过变分得到其弱形式,进行类似推导可得线性方程组

(6)

3 结 论

对于函数最佳平方逼近,利用向量空间的空间投影推导,可将复杂的运算转化为学生非常熟悉的线性代数问题,而且几何意义非常直观.此外,通过将相关结论推广到最小二乘法,微分方程的Galerkin方法求解,可将这一类问题理解成最佳逼近(在某种意义下),或者是不同空间的投影.该教学内容的相关处理,可使学生更容易掌握与应用函数最佳逼近,最小二乘法以及微分方程Galerkin方法求解等知识.相关处理方法可促进学生在学习中提高整体把握,融会贯通的能力.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.