矩阵的Kronecker积的性质
李 俊, 戴星宇, 宋伊萍
(国防科技大学 理学院,长沙 410072)
0 引 言
矩阵的Kronecker积是矩阵的一种重要乘积,在信号处理、随机过程向量分析、群论、数值分析等领域中都有着广泛应用. 大部分教材中除了会介绍Kronecker积的基本性质外,还会给出Kronecker积的特征值、特征向量、秩、迹和行列式等重要结果[1-2],但是对于Kronecker积的Jordan标准形、最小多项式、范数和分解等内容基本没有介绍,文献[3]中给出了Kronecker积的几个范数公式,文献[4]通过行列式因子法给出Kronecker积的Jordan标准形,文献[5]通过分析Jordan块的幂的秩的变化规律给出Kronecker积的Jordan标准形. 本文通过初等变换法给出Kronecker积的Jordan标准形的一种新的证明方法,进而给出关于Kronecker积的Jordan标准形、最小多项式、范数和分解的相关结果.
1 预备知识
先约定文中的记号:A⊗B表示矩阵A和B的Kronecker积,En表示n阶的单位矩阵,Jr1(λ1)表示λ1对应的r1阶Jordan块,JA表示矩阵A的Jordan标准形,di(λ)表示相应矩阵的第i个不变因子,Di(λ)表示相应矩阵的第i阶行列式因子.除特殊声明外,本文所考虑的矩阵都是方阵.
引理1[2,5]若A和B分别是下三角矩阵、单位下三角矩阵、上三角矩阵、单位上三角矩阵、对角矩阵、酉矩阵、行满秩矩阵、列满秩矩阵、Hermite正定矩阵、Hermite半正定矩阵,则A⊗B也是下三角矩阵、单位下三角矩阵、上三角矩阵、单位上三角矩阵、对角矩阵、酉矩阵、行满秩矩阵、列满秩矩阵、Hermite正定矩阵、Hermite半正定矩阵.
引理2假设λ1,μ1∈,且λ1μ1≠0,r1,t1都是正整数.若r1≥t1,则λ矩阵(λEt1-λ1Jt1(μ1))r1的不变因子为
d1(λ)=(λ-λ1μ1)r1-t1+1,d2(λ)=(λ-λ1μ1)r1-t1+3,…,
dk(λ)=(λ-λ1μ1)r1-t1+2k-1, …,dt1(λ)=(λ-λ1μ1)r1+t1-1.
若r1 d1(λ)=…=dt1-r1(λ)=1,dt1-r1+1(λ)=(λ-λ1μ1)r1-t1+1, dt1-r1+2(λ)=(λ-λ1μ1)r1-t1+3, …,dt1(λ)=(λ-λ1μ1)r1+t1-1. 由矩阵Cr1的元素排列的规律可知,随着列数增加每一列的非零元素对应的因式λ-λ1μ1的次数减少,随着行数减少每一行的非零元素对应的因式λ-λ1μ1的次数减少,因此Cr1的k阶非零子式中因式λ-λ1μ1的次数至少是k(r1-t1+k),即矩阵Cr1的k阶行列式因子实质上是由该矩阵中取第1,2,…,k行和第t1-k+1,t1-k+2,…,t1列的非零k阶子式来确定,进而由行列式因子的定义知 D1(λ)=(λ-λ1μ1)r1-t1+1,D2(λ)=(λ-λ1μ1)2(r1-t1+2),…, Dk(λ)=(λ-λ1μ1)k(r1-t1+k), …,Dt1(λ)=(λ-λ1μ1)r1t1. 令d1(λ),d2(λ),…,dt1(λ)表示(λEt1-λ1Jt1(μ1))r1的不变因子,则 Dk(λ)=d1(λ)d2(λ)…dk(λ),k=1,2,…,t1. 因此λ矩阵(λEt1-λ1Jt1(μ1))r1的不变因子为 d1(λ)=(λ-λ1μ1)r1-t1+1,d2(λ)=(λ-λ1μ1)r1-t1+3,…, dk(λ)=(λ-λ1μ1)r1-t1+2k-1, …,dt1(λ)=(λ-λ1μ1)r1+t1-1. 若r1 Dt1-r1(λ)=1,Dt1-r1+1(λ)=(λ-λ1μ1)t1-r1+1,…, Dt1-k(λ)=(λ-λ1μ1)(t1-k)(r1-k), …,Dt1(λ)=(λ-λ1μ1)t1r1. 因此λ矩阵Cr1的不变因子为 d1(λ)=…=dt1-r1(λ)=1,dt1-r1+1(λ)=(λ-λ1μ1)r1-t1+1, dt1-r1+2(λ)=(λ-λ1μ1)r1-t1+3, …,dt1(λ)=(λ-λ1μ1)r1+t1-1. 解对λ矩阵C进行初等变换 因此λ矩阵C的不变因子为d1(λ)=1,d2(λ)=(λ-6)2,d3(λ)=(λ-6)4. 因此λ矩阵F的不变因子为d1(λ)=λ-6,d2(λ)=(λ-6)3,d3(λ)=(λ-6)5. 关于矩阵A和B的Kronecker积A⊗B的Jordan标准形,有如下结果. 定理1设矩阵A和B的Jordan标准形分别为 JA=diag(Jr1(λ1),Jr2(λ2),…,Jrs(λs)), JB=diag(Jt1(μ1),Jt2(μ2),…,Jtk(μk)), 则A⊗B的Jordan标准形是由Jri(λi)⊗Jtj(μj),1≤i≤s,1≤j≤k对应的Jordan块构成. 证因为JA⊗B~A⊗B,A⊗B~JA⊗JB,所以JA⊗B~JA⊗JB.因此JA⊗JB的Jordan标准形也是A⊗B的Jordan标准形.由于 而 是分块对角矩阵,因此只需要确定每一块的Jordan标准形,就可以得到A⊗B的Jordan标准形.因此A⊗B的Jordan标准形是由Jri(λi)⊗Jtj(μj)对应的Jordan块构成,1≤i≤s,1≤j≤k. 下面给出两个Jordan块的Kronecker积的Jordan标准形. 定理2[4-5]设A=Jr1(λ1),B=Jt1(μ1),令r=max{r1,t1},t=min{r1,t1}. (i) 若λ1μ1≠0,则A⊗B的Jordan标准形是从Jr-t+1(λ1μ1)开始阶数依次增加2的t个Jordan块构成,即 JA⊗B=diag(Jr-t+1(λ1μ1),Jr-t+3(λ1μ1),…,Jr+t-1(λ1μ1)); (ii) 若λ1≠0,μ1=0,则A⊗B的Jordan标准形是由r1个Jordan块Jt1(0)构成,即 JA⊗B=diag(Jt1(0),Jt1(0),…,Jt1(0)); (iii) 若λ1=0,μ1≠0,则A⊗B的Jordan标准形是由t1个Jordan块Jr1(0)构成,即 JA⊗B=diag(Jr1(0),Jr1(0),…,Jr1(0)); (iv) 若λ1=μ1=0,则A⊗B的Jordan标准形是由2个1阶Jordan块J1(0),2个2阶 的Jordan块J2(0),…,2个t-1阶的 Jordan块Jt-1(0),r-t+1个t阶的Jordan块Jt(0)构成,即 JA⊗B=diag(J1(0),J1(0),…,Jt-1(0),Jt-1(0),Jt(0),…,Jt(0)). (i) 由于λ1μ1≠0,令C=λEt1-λ1Jt1(μ1),则对λE-A⊗B进行一系列初等变换 由引理2知,λE-A⊗B的不变因子为 d1(λ)=…=dt1(r1-1)(λ)=1,dt1(r1-1)+1(λ)=(λ-λ1μ1)r1-t1+1, dt1(r1-1)+2(λ)=(λ-λ1μ1)r1-t1+3, …,dt1r1(λ)=(λ-λ1μ1)r1+t1-1, 因此 JA⊗B=diag(Jr-t+1(λ1μ1),Jr-t+3(λ1μ1),…,Jr+t-1(λ1μ1)). 再通过适当的列变换和行变换最终就可将λE-A⊗B的前t1行化成 diag(D,…,D,λE-λ1Jt1(μ1)). 由于λE-λ1Jt1(μ1)的不变因子为d1(λ)=…=dt1-1(λ)=1,dt1(λ)=λt1,故λE-A⊗B的不变因子为 d1(λ)=…=dr1(t1-1)(λ)=1,dr1(t1-1)+1(λ)=…=dr1t1(λ)=λt1. 即A⊗B的初等因子为是r1个λt1,因此A⊗B的Jordan标准形为 JA⊗B=diag(Jt1(0),Jt1(0),…,Jt1(0)). (iii) 由于λ1=0,μ1≠0,故 于是 进而λE-A⊗B通过初等变换可化成diag(Et1,…,Et1,λr1Et1),故λE-A⊗B的不变因子为 d1(λ)=…=dt1(r1-1)(λ)=1,dt1(r1-1)+1(λ)=…=dt1r1(λ)=λr1. 即A⊗B的初等因子是t1个λr1,因此A⊗B的Jordan标准形为 JA⊗B=diag(Jr1(0),Jr1(0),…,Jr1(0)). (iv) 由于λ1=μ1=0,令C=λE-A⊗B,则 其中 对矩阵C进行类似的变换,最终可以得到 其中F,G1,G2,H1,H2如上, 故C的不变因子为 d1(λ)=…=dt1(r1-2)-s+2(λ)=1,dt1(r1-2)-s+3(λ)=dt1(r1-2)-s+4(λ)=λ,…, dt1r1-s-1(λ)=dt1r1-s(λ)=λt-1,dt1r1-s+1(λ)=…=dt1r1(λ)=λt, 其中λ,λ2,…,λt-1各有2个,λt有s个.因此A⊗B的Jordan标准形为 JA⊗B=diag(J1(0),J1(0),…,Jt-1(0),Jt-1(0),Jt(0),…,Jt(0)), 其中Jt(0)有|r1-t1|+1块. 注 定理2中的情形(i)中的具体情形: 当r1≤t1时, JA⊗B=diag(Jt1-r1+1(λ1μ1),Jt1-r1+3(λ1μ1),…,Jt1+r1-1(λ1μ1)); 当r1≥t1时, JA⊗B=diag(Jr1-t1+1(λ1μ1),Jr1-t1+3(λ1μ1),…,Jr1+t1-1(λ1μ1)). 因此λE-A1⊗B1的不变因子为 d1(λ)=d2(λ)=d3(λ)=d4(λ)=1,d5(λ)=(λ-6)2,d6(λ)=(λ-6)4. 故 通过类似计算可分别求得A1⊗B2,A2⊗B1,A2⊗B2的Jordan标准形,即 假设矩阵A和B的最小多项式分别为 mA(λ)=(λ-λ1)m1(λ-λ2)m2…(λ-λs)ms, mB(λ)=(λ-μ1)n1(λ-μ2)n2…(λ-μk)nk, 则矩阵A的相异特征值只有λ1,λ2,…,λs,并且A的Jordan标准形中对应的Jordan块中最高阶数分别为m1,m2,…,ms,矩阵B的相异特征值只有μ1,μ2,…,μk,并且B的Jordan标准形中对应的Jordan块中最高阶数分别为n1,n2,…,nk.由矩阵的Jordan标准形与最小多项式之间的关系以及定理2可得下列定理. 定理3已知矩阵A和B的最小多项式分别为 mA(λ)=(λ-λ1)m1(λ-λ2)m2…(λ-λs)ms, mB(λ)=(λ-μ1)n1(λ-μ2)n2…(λ-μk)nk, 令tij=min{mi,nj},1≤i≤s,1≤j≤k. (i) 若λiμj≠0且λiμj两两不同,1≤i≤s,1≤j≤k,则A⊗B的最小多项式 (ii) 若存在1≤i0≤s,1≤j0≤k使得λi0=μj0=0,且λiμj两两不同,1≤i≠i0≤s,1≤j≠j0≤k,则A⊗B的最小多项式 (iii) 若存在1≤i0≤s,使得λi0=0,且λiμj两两不同,1≤i≠i0≤s,1≤j≤k,则A⊗B的最小多项式 (iv) 若存在1≤j0≤k使得μj0=0,且λiμj两两不同,1≤i≤s,1≤j≠j0≤k,则A⊗B的最小多项式 (v) 若上述四种情况中连乘部分只要出现一次因式相同的情形,则只保留相同一次因式中方幂次数最高的那一项,而该一次因式方幂次数低的项直接舍去. 解由例2可知矩阵A1⊗B1,A1⊗B2,A2⊗B1,A2⊗B2的Jordan标准形分别为 由最小多项式与Jordan标准形的关系可知,A1⊗B1,A1⊗B2,A2⊗B1,A2⊗B2的最小多项式分别为 mA1⊗B1(λ)=(λ-6)4,mA1⊗B2(λ)=λ3,mA2⊗B1(λ)=λ2,mA2⊗B2(λ)=λ2. 这与定理3中的结论是一致的. 由于矩阵可相似对角化当且仅当矩阵的最小多项式是互不相同的一次因式的乘积,故有下列推论. 推论1[5]已知A∈m×m和B∈n×n都是非零矩阵,则A⊗B可相似对角化的充分必要条件是A和B都可相似对角化. 证充分性容易证明.下面采用定理3中记号约定,若A∈m×m和B∈n×n都是非零矩阵,并且A⊗B可相似对角化,因此A⊗B的最小多项式是互不相同的一次因式的乘积,由于mi≥1,nj≥1,1≤i≤s,1≤j≤t,并且定理3中的四种情况分别对应着 (1)mi+nj-1=1,1≤i≤s,1≤j≤t; (2)ti0j0=min{mi0,nj0}=1,mi+nj-1=1,1≤i≠i0≤s,1≤j≠j0≤t; (3)mi0=1,mi+nj-1=1,1≤i≠i0≤s,1≤j≤t; (4)nj0=1,mi+nj-1=1,1≤i≤s,1≤j≠j0≤t; 因此mi=1,nj=1,1≤i≤s,1≤j≤t,即A和B的最小多项式都是互不相同的一次因式的乘积,故A和B都可相似对角化. 为了完整起见,本节将已有的Kronecker积的常见矩阵范数性质进行了罗列,此外还给出Kronecker积的常见分解的相关结果. 性质1[3]已知矩阵A∈m×m和B∈n×n,则 ‖A⊗B‖1=‖A‖1‖B‖1, ‖A⊗B‖∞=‖A‖∞‖B‖∞, ‖A⊗B‖2=‖A‖2‖B‖2, ‖A⊗B‖F=‖A‖F‖B‖F, ‖A⊗B‖m1=‖A‖m1‖B‖m1, ‖A⊗B‖mp=‖A‖mp‖B‖mp, ‖A⊗B‖m∞=‖A‖m∞‖B‖m∞. 由引理1可知,关于矩阵A∈m×m,B∈n×n的Kronecker积的三角分解、QR分解、满秩分解、奇异值分解、极分解有如下性质. 性质2若A=L1R1和B=L2R2分别是矩阵A和B的三角(Doolittle,Crout)分解,则 A⊗B=(L1⊗L2)(R1⊗R2) 为矩阵A⊗B的三角(Doolittle,Crout)分解. 证若A=L1R1和B=L2R2分别是矩阵A和B的三角分解,即L1,L2是下三角矩阵,R1,R2是上三角矩阵,由引理1知L1⊗L2是下三角矩阵,R1⊗R2是上三角矩阵,因此A⊗B=(L1⊗L2)(R1⊗R2)为矩阵A⊗B的三角分解. 特别地,若A=L1R1和B=L2R2分别是矩阵A和B的Doolittle分解(或Crout分解),则L1,L2是单位下三角矩阵(或R1,R2是单位上三角矩阵),由引理1知L1⊗L2也是单位下三角矩阵(或R1⊗R2是单位上三角矩阵),因此A⊗B=(L1⊗L2)(R1⊗R2)为矩阵A⊗B的Doolittle分解(或Crout分解). 性质3若A=L1D1R1和B=L2D2R2分别是矩阵A和B的LDR分解,则 A⊗B=(L1⊗L2)(D1⊗D2)(R1⊗R2) 为矩阵A⊗B的LDR分解. 证若A=L1D1R1和B=L2D2R2分别是矩阵A和B的LDR分解,即L1,L2是单位下三角矩阵,D1,D2是对角矩阵,R1,R2是单位上三角矩阵,由引理1知L1⊗L2是单位下三角矩阵,D1⊗D2是对角矩阵,R1⊗R2是单位上三角矩阵,因此 A⊗B=(L1⊗L2)(D1⊗D2)(R1⊗R2) 为矩阵A⊗B的LDR分解. A⊗B=(G1⊗G2)(G1⊗G2)H 为矩阵A⊗B的Cholesky分解. A⊗B=(G1⊗G2)(G1⊗G2)H 为矩阵A⊗B的Cholesky分解. 性质5[5]若A=Q1R1和B=Q2R2分别是矩阵A和B的QR分解,则 A⊗B=(Q1⊗Q2)(R1⊗R2) 为矩阵A⊗B的QR分解. 性质6若A=F1G1和B=F2G2分别是矩阵A和B的满秩分解,则 A⊗B=(F1⊗F2)(G1⊗G2) 为矩阵A⊗B的满秩分解. 证若A=F1G1和B=F2G2分别是矩阵A和B的满秩分解,即F1,F2是列满秩矩阵,G1,G2是行满秩矩阵,由引理1知F1⊗F2是列满秩矩阵,G1⊗G2是行满秩矩阵,因此 A⊗B=(F1⊗F2)(G1⊗G2) 为矩阵A⊗B的满秩分解. A⊗B=(U1⊗U2)(Σ1⊗Σ2)(V1⊗V2)H 为矩阵A⊗B的奇异值分解. 性质8[6]若A=C1Q1=Q1D1和B=C2Q2=Q2D2分别是矩阵A和B的极分解,其中Q1和Q2是酉矩阵,C1,D1,C2,D2是Hermite半正定矩阵,则 A⊗B=(C1⊗C2)(Q1⊗Q2)=(Q1⊗Q2)(D1⊗D2) 为矩阵A⊗B的极分解. 证若A=C1Q1=Q1D1和B=C2Q2=Q2D2分别是矩阵A和B的极分解,其中Q1和Q2是酉矩阵,C1,D1,C2,D2是Hermite半正定矩阵,由引理1知Q1⊗Q2是酉矩阵,C1⊗C2是Hermite半正定矩阵,D1⊗D2是Hermite半正定矩阵,因此 A⊗B=(C1⊗C2)(Q1⊗Q2)=(Q1⊗Q2)(D1⊗D2) 为矩阵A⊗B的极分解. 本文通过初等变换法给出矩阵A和B的Kronecker积A⊗B的Jordan标准形与A和B的Jordan标准形之间的关系,以及Kronecker积A⊗B的最小多项式与A和B的最小多项式之间的关系,由此证明了矩阵的Kronecker积A⊗B可对角化当且仅当矩阵A和B都可对角化. 此外本文还总结了Kronecker积A⊗B的各种范数以及分解与矩阵A和B的相应范数和分解的关系. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.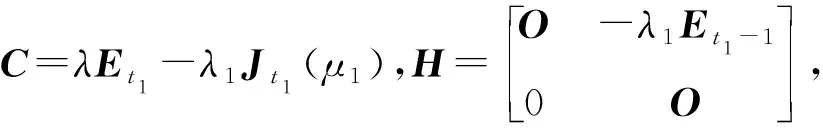

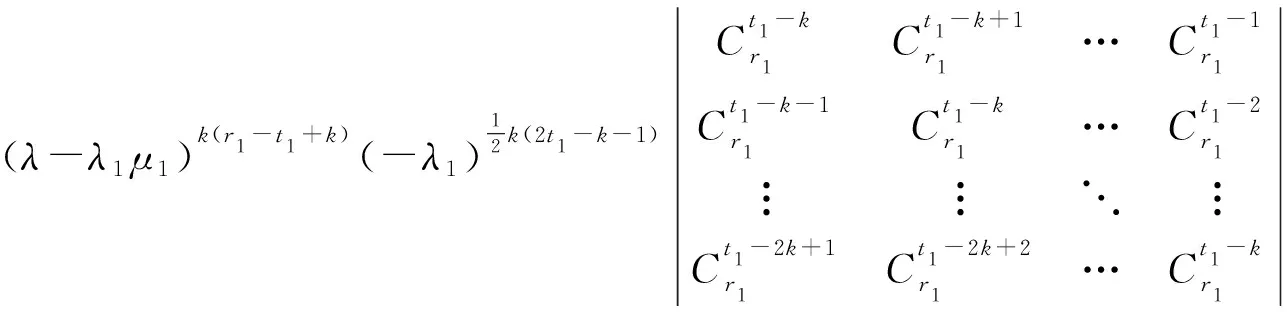
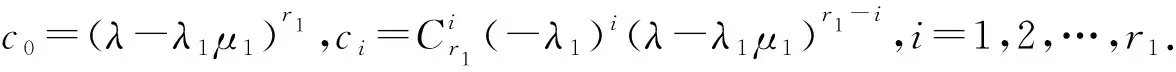
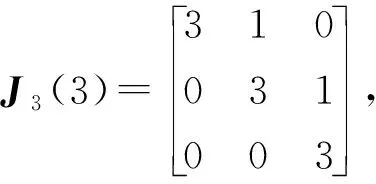
2 Kronecker积的Jordan标准形



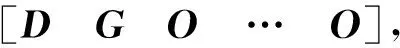
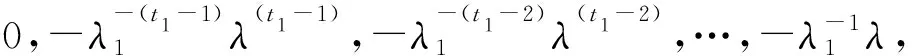
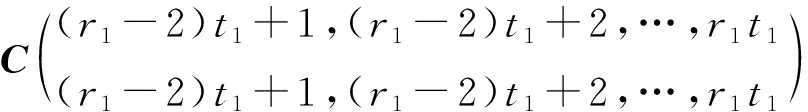
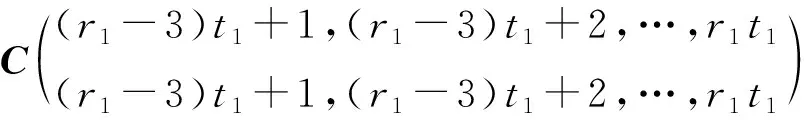
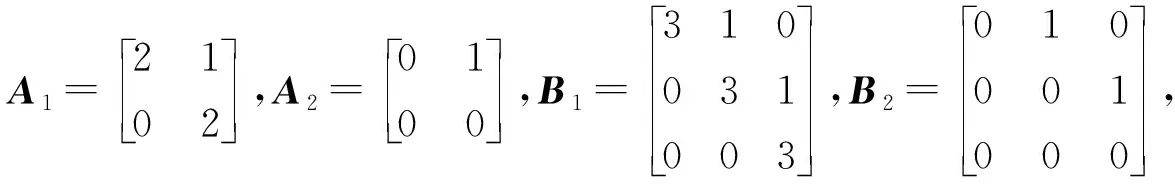

3 Kronecker积的最小多项式
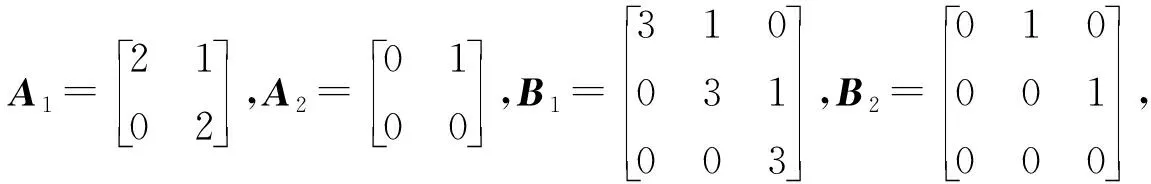
4 Kronecker积的范数和分解
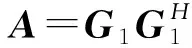
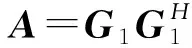

5 结 论

