结合近邻密度和信息修正的基本概率赋值生成方法

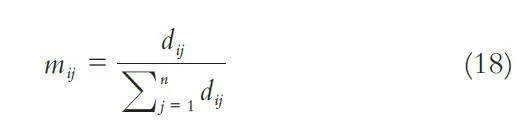
摘 要：为了解决D-S 证据理论应用中基本概率赋值（BPA）获取困难、生成模型适用度低的问题， 提出一种结合近邻密度和信息修正的基本概率赋值生成方法： 通过基于KNN 算法得出的密度峰值点与样本间的距离为依据生成单焦元BPA 函数， 通过信念χ2 散度对全子集事件赋值并基于可信度对BPA 进行信息修正， 用改进的信念熵公式计算各证据的不确定性权重， 进行证据的再分配. 利用生成的BPA 解决少样本和不均衡类样本的实际应用问题， 经多个数据集验证诊断精度均达85% 以上， 优于其他方法.

关键词：D-S 证据理论; 密度; 信息修正; 信念熵; 信念χ2 散度

中图分类号：TP391

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.01

D-S 证据理论[1]是处理不确定性信息的有效方法， 与贝叶斯算法成为数据融合中的两个主流经典算法. 相比于贝叶斯算法， D-S 证据无需先验概率且可以将概率同时赋给单焦元子集和多焦元子集，在决策[2-5]、分类[6-7]、模式识别[8-10]、数据融合[11]等诸多领域得到广泛应用. 然而， Zadeh 提出“Zadeh 悖论[12]”对D-S 证据理论质疑. 他认为当使用D-S 组合规则融合高度冲突的证据时， 会获得违反直觉的结果. 为解决此问题， 研究人员开展了大量研究， 目前已有的研究方法可以分为修改D-S 的组合规则[13]和对证据进行预处理[14]两大类. 对于这两类解决方法， D-S 理论终究是针对各个证据的基本概率赋值（The basic probability assignment function， BPA）进行融合. 若BPA 函数是客观合理的， 会减少大量对证据的后续修正处理工作. 因此， 就如何生成BPA 这一问题， 一直以来都是D-S 证据理论框架下的研究焦点， 可至今没有统一的定论.

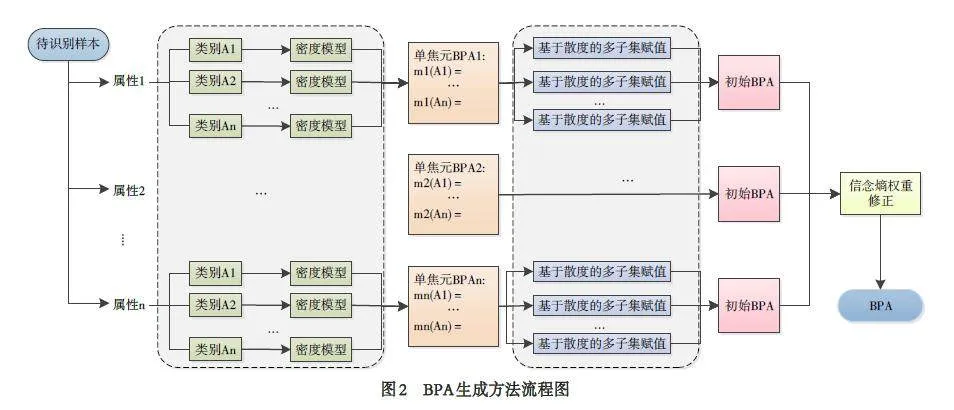
早期针对BPA 函数的生成方法主要以专家主观经验为依据分配信任值， 但是该方法受主观影响较大， 不同专家给出的信任值往往会存在一定的冲突. 目前使用的BPA 函数的生成方法主要是根据系统的应用背景和客观条件自动生成BPA， 例如工业背景下的系统故障率. 但该方法需要相对完备的数据基础和相对完善的硬件设施， 受限程度较大. 因此， 国内外学者目前对该问题的探索多数仍然是以解决实际应用为导向， 基于应用背景进行概率赋值. 较早的Bogler 等人[15]利用目标速度和加速度或目标身份构建BPA; 文献[16]根据传感器节点所测得的水质数据与水质等级标准之间的距离为依据生成BPA; 文献[17]通过传感器监测数据对实体特征指标进行计算得到BPA. 此种研究思路下， BPA 的构建方法没有一个固定的模式， 通常是根据应用背景提出设计思路， 获得BPA. 但随着D-S 证据理论的应用愈加广泛， 越来越多的学者意识到BPA 生成的重要性， 开始研究适用性较高的基本概率分配方法. 韩崇昭等人[18]提出一种基于最大熵原则构建BPA 的方法; 文献[19]构建样本的区间数模型， 通过区间数距离表示样本之间的差异性， 并依此生成BPA， 该方法的结果易受异常值影响而出现较大偏差; 文献[20]提出了基于高斯分布的单焦元BPA 生成方法， 但是忽视了多焦元子集的赋值问题; 文献[21]将BP 神经网络的输出结果作为基本概率分配的值， 其应用要求数据相对完善且分布均衡; 蒋雯等人[22]提出了基于广义模糊数构建基本概率赋值函数; 文献[23]为数据的每个属性建立基于正态分布的模型， 然后利用数据与正态分布模型之间的关系，构造嵌套结构的BPA 函数. 根据对现有文献分析可以看出， BPA 函数的生成本质是基于样本数据， 对各可能事件发生概率的确定. 目前多数学者使用的BPA 生成方法大都需要足够的样本为依据进行估算. 而在很多实际应用场景中， 如网络安全领域， 收集和标注大量网络中的新型未知攻击样本是十分困难的， 则建立目标属性的描述模型可用样本较少[24].因此本文提出一种结合近邻密度和信息修正的基本概率赋值生成方法. 该方法首先基于样本近邻密度构建目标模型值， 利用待测样本与目标模型值之间距离差异度生成单焦元BPA; 然后提出了一种基于信念χ2 散度的多焦元BPA 分配方法和改进的信念熵公式， 对基本概率赋值函数进行可信度与不确定性双重修正并对多焦元子集进行赋值， 从而得到目标问题的基本概率分配; 最后通过多个UCI 数据集对本文所提出的方法进行有效性验证.

1 相关理论基础

1.1 D-S 证据理论

D-S 证据理论主要用于处理不确定信息. 对于目标分类而言， 某一类事件的发生往往伴随多角度的属性特征， 每个特征下该目标事件皆存在一定的发生可能性. 该理论是利用事件发生时， 产生的多维度特征值来确定目标类型. D-S 证据理论通过计算对不同属性特征的基本概率分配函数， 并运用D-S 证据理论合成规则对其进行融合， 使判定结论更加合理， 置信度更高. 下面给出与本文研究相关的D-S 证据理论定义.

定义1 识别框架： 假定Θ = {A } 1，A2，…An 是给定问题所有可能发生结果的有限集合， 且其中元素互斥， 则称该类集合为识别框架. 识别框架Θ的幂集用2Θ 表示， 具体描述为： 2Θ = { ∅， { A1 } ，…{ An } ， { A1，A2 } ， { A1，A3 } ，…{ A1，A2，…An - 1 } ，…Θ }其中∅表示空集.

定义2 基本概率赋值函数： 假设映射m：2Θ → [ 0，1]， 若满足条件：

则称Bel （ A）为命题A 的信任函数.

定义5 似然函数： 对给定的证据m， 定义似然函数， 似然函数值Pl （ A） 表示证据对命题A 不为假的信任程度.

若映射m：2Θ → [ 0，1]满足：Pl （ A） = ΣB ⋂ A ≠ ∅m （B ） = 1 - Bel （ Aˉ） ，∀A ⊆ Θ （5）则称Pl （ A）为该命题的似然函数.

信任函数是指明确支持A 事件的概率之和， 它反映了A 的必然性和信任度， 构成了A 的概率的下限函数; 而似然函数则度量了潜在支持A 事件的概率之和， 它描述了与A 相关的总的信任度， 构成了A的概率的上限函数. 即Bel （ A） ≤ m （ A） ≤ Pl （ A）.

1.2 KNN 密度峰值算法

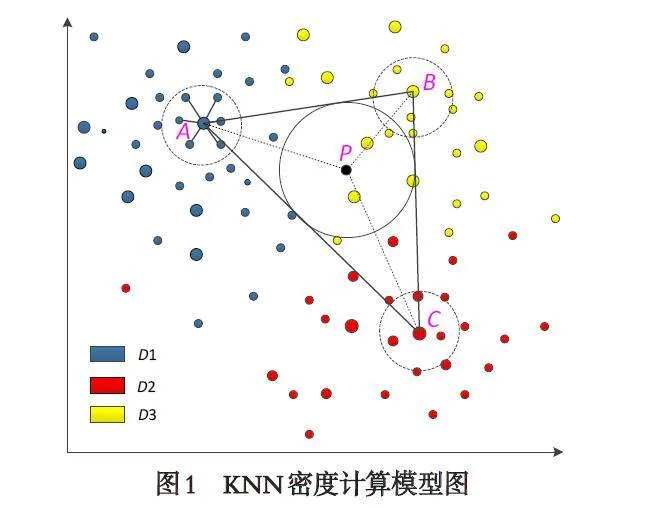
K-近邻（KNN）是经典的分类方法之一， 依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别. 当对数据的分布很少或者没有任何先验知识时， K 近邻算法可以达到相对较高的准确率. 本文基于该思想， 在局部类内以每点为中心不断搜索其周边K 个近邻点的位置信息并计算两者距离， 即点的K 近邻密度取决于它与K 近邻点集的距离之和. 在相对密集的区域， 该点的K 近邻点距离之和较小; 相反， 越稀疏K 近邻点距离之和越大， 这可以表明该点在一个类簇的密集程度. 将样本按近邻密度进行降序排列， 获取密度位于前3 的待测样本， 通过降维得到其二维坐标. 若三点坐标位于同一直线， 则对两端点坐标求平均; 否则将如图1 所示， 构成以A、B、C 为顶点的三角形并求其内心坐标P （x，y ）， 距离内心最近的数据样本则为特征模型值.

计算如下：

设i = {a } 1，a2，…，an 为任一样本点，n 为样本属性个数， j = {b } 1，b2，…，bn 为i 的K 个近邻点之一， 则其密度Di 定义为：

即D'i 越大， 代表待测样本距离K 个近邻点距离越远， 密度越小. 选取近邻密度相对较高的前三个样本点所对应的二维坐标作为A、B、C 点， 通过公式（9）确定内心坐标，通过近邻分析查找距离内心最近的样本点作为特征模型值.

（2）基于待识别样本值之间的距离， 生成初始单焦元BPA 函数：

其中： dij 表示当前样本x 与每一类目标模型值Dij 对应属性间的距离倒数， i = 1，2，…，n ; j = 1，2，…，m， m为列属性个数， n 为样本类别数. 每个样本根据n 类特征值将生成n × m 的距离矩阵， 记为DDIS_ ij. 例如：{d } 11，d12，…d1m 表示当前样本与第一类模型值对应属性间的距离倒数. 以距离倒数衡量待测样本与目标属性值之间的差异度， dij 越大， 则与目标值归属同一类的可能性越大. 对各样本的距离测度进行归一化处理， 将各样本的距离权重作为初始单焦元BPA 函数， 公式如下：

Step2： 全子集概率分配与可信度修正

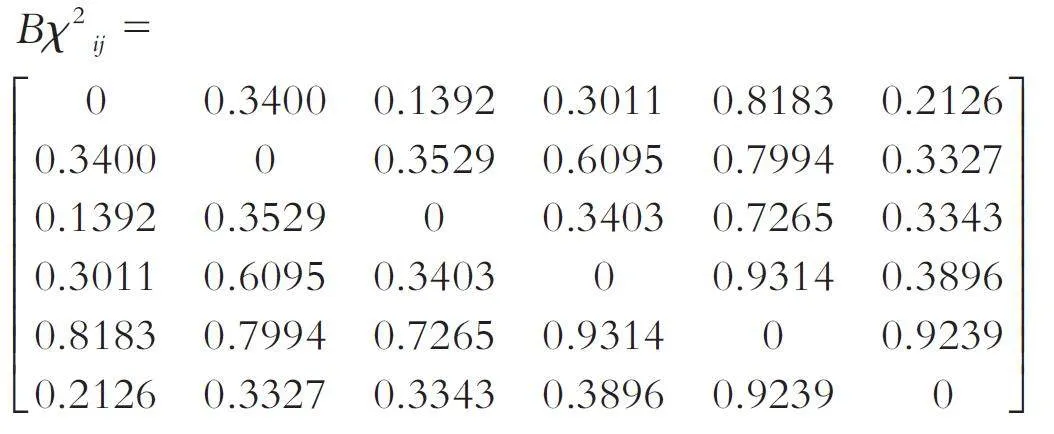
（1）计算证据间散度距离. 根据色式（11）计算各证据间的信任散度距离， 并得各证据间的距离矩阵：

其中Bχ2ij 表示证据mi 和mj 之间的信任散度距离，Bχ2 越大， 则表明两证据间信任度越低. 由公式（11）易知， Dii = 0且Dij = Dji， Bχ2ij 为对称矩阵.

（2）多焦元概率分配. 通过公式（12）（13）对生成BPA 进行可信度修正， 并对全子集事件赋值.

Step3： 不确定性权重的构造与BPA 修正

基于改进的信念熵计算方法度量信息的不确定性. 通过公式（15）计算各证据间的不确定性， 将结果记为Eb （m ） i ， 每个类别具有的属性为i （i = 1，2，…，n），n 为属性总数. 并对结果进行归一化处理得到不确定性权重iwi =Eb （mi ）／Σi = 1n Eb （mi ）， 修正步骤2 所得BPA结果. 对可靠性较低的BPA 函数赋予较低权重， 降低其干扰性. 随后， 对生成的BPA 计算加权平均证据.

Step4： BPA 融合识别

将待分类样本每种属性下计算所得BPA 按照公式（2）和公式（3）进行融合， 将融合结果中具有最大信度的事件作为识别结果.

2.2 算例分析

用UCI 上公开的骨科患者的生物力学特征数据集分类问题验证本文提出的BPA 生成方法的有效性. 该数据集有三个分类， 分别是腰椎突出（Her⁃nia）、脊椎滑脱（Spondylolisthesis）和正常（Normal）， 样本量依次是60、150 和100， 样本量偏少且存在一定程度的分布不均衡. 分别用A1、A2、A3 来表示， 由三种状态组成的一个识别框架为Θ = {A } 1，A2，A3 .其中每个样本有六个属性特征， 分别是骨盆入射角PI（pelvic incidence）、骨盆倾斜PT（pelvic tilt）、腰椎前凸角度LLA（lumbar lordosis angle）、骶骨倾斜角SS（sacral slope）、盆腔半径PR（pelvic radius）、脊椎前移的等级GOS（grade of spondylolisthesis）. 获取BPA 后， 采取经典的Dempster 组合规则并选择融合后具有最大信度的焦元命题作为识别方案， 具体流程如下.

步骤1： 构造单焦元子集模型

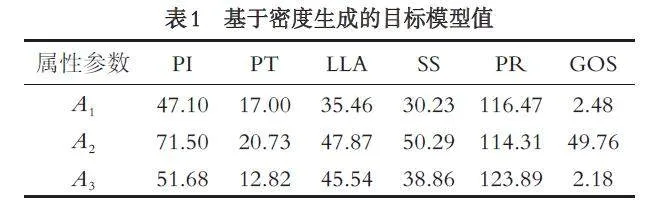
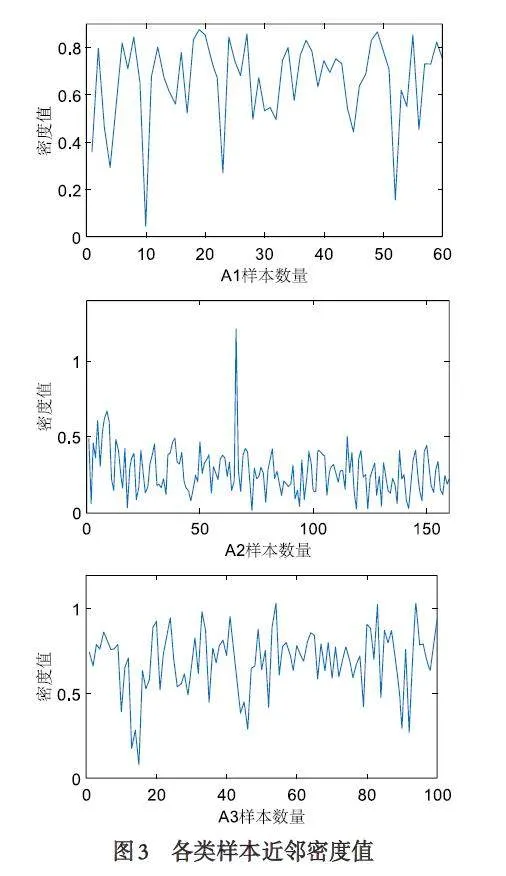
对于这三类脊椎状况的数据样本， 使用基于KNN 的密度峰值筛选算法， 得到三类样本近邻密度值（如图3）.根据Step-1 确定特征模型值（如表1）.

例： 数据样本S1 = { 39.05， 10.06， 25.01， 28.99，114.4， 4.56 }， 计算S1 对目标属性A1 的基本概率分配. 通过公式（17）得到距离矩阵：

DDIS_S1 ， A1 =

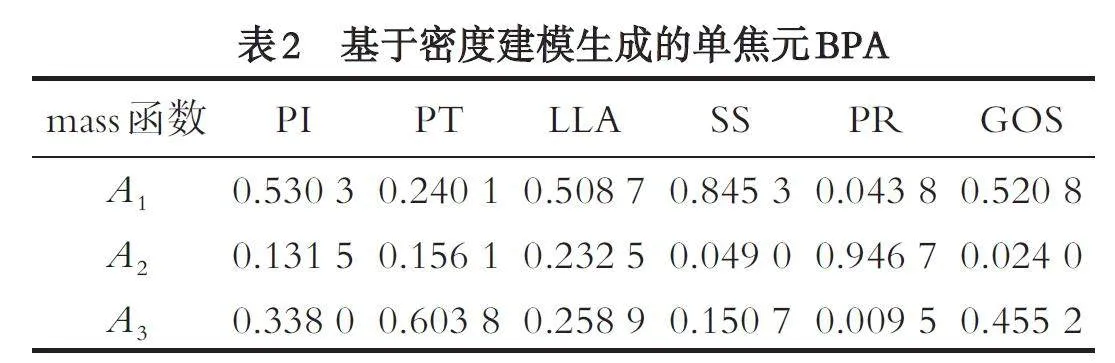
通过式（18）， 可以得到待测样本S1 对脊椎健康Hernia 等级的mass 函数值为： mA1S1 = {0.5303， 0.2401，0.5087， 0.8453， 0.0438， 0.5208}. 类似地， 可以得到健康等级A2 和A3 的各mass 函数值， 结果如表2 所示.

步骤2： 多焦元概率分配与可信度修正

基于信念χ2 散度生成可信度权重， 并给系统未知性赋值. 利用公式（11）计算表2 中各证据间的Bχ2距离， 生成对称的距离矩阵如下：

根据两证据间的平均相似度来度量各证据的可信度， 结果如下：

α1 = 0.3622 ; α2 = 0.4869 ; α3 = 0.3786

α4 = 0.5143 ; α5 = 0.8399 ; α6 = 0.4386

其归一化结果为：

ω1 = 0.1199 ; ω2 = 0.1611 ; ω3 = 0.1253

ω4 = 0.1703 ; ω5 = 0.2781 ; ω6 = 0.1452

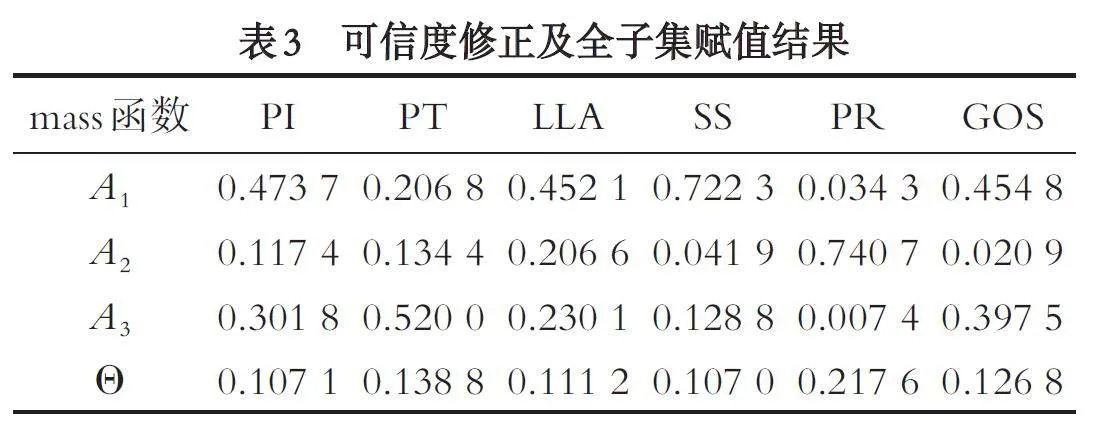
通过公式（12）（13）对各单焦元BPA 进行可信度的修正并对全子集事件进行赋值. 结果如表3 所示.

步骤3： 不确定性权重的构造与BPA 修正

在上一步骤的基础上， 利用本文改进的新信念熵来度量证据不确定性. 根据公式（15）对表3 内的基本概率赋值函数计算信念熵， 结果如下：

Eb （m1 ） = 1.7402 ; Eb （m2 ） = 1.7453 ;

Eb （m3 ） = 1.8277 ; Eb （m4 ） = 1.2566 ;

Eb （m5 ） = 1.0188 ; Eb （m6 ） = 1.5404

对各证据的信念熵测度进行归一化处理， 得：

iw1 = 0.1906， iw2 = 0.1912， iw3 = 0.2002

iw4 = 0.1376， iw5 = 0.1116， iw6 = 0.1687

将上述归一化得到的信念熵结果， 与表4 各mass 函数值进行修正得到加权平均证据， 结果如下：

m （ A1 ） = 0.4004， m （ A2 ） = 0.1811

m （ A3 ） = 0.2878， m （Θ） = 0.1296

步骤4： BPA 融合识别

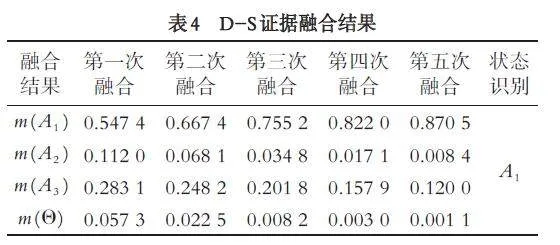
通过D-S 证据融合规则对上述加权平均证据进行n - 1 次融合， 结果如表4 所示. 根据最终组合结果可判断脊椎状态.

由表4 可得， 第一次融合后PI 对A1 的信任值为0.547 4， 相较于融合前信任值为0.400 4 再到最终融合结果为0.870 5， 显著提高了诊断精度. 对于属性SS 和属性PR 中出现的证据高度冲突的情况， 本文方法也可以在融合中作出正确决策.

3 实验与结果分析

采用在UCI 公开的几个数据集作为验证数据集验证本文提出的BPA 生成方法在分类诊断方面应用的有效性， 并与其他方法进行对比; 为了进一步验证本文方法在少样本数据下的有效程度， 参考康兵义[19]等人提出的小样本测试方法， 对样本规模做单变量分析.

3.1 常规数据下识别的有效性

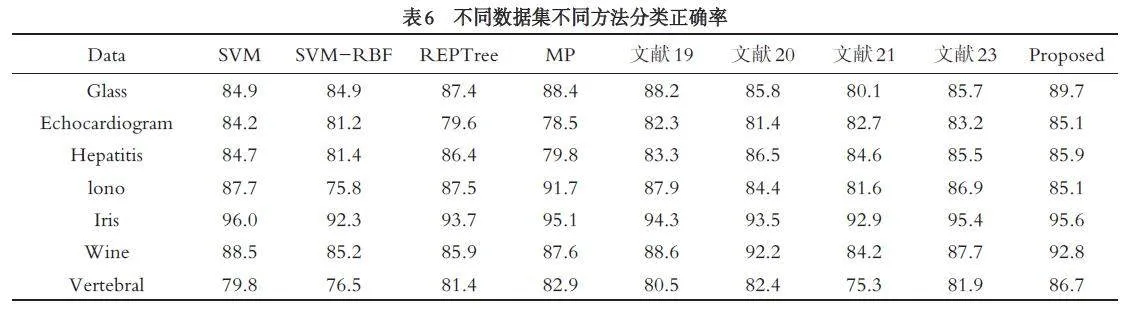
实验采用的7 个在UCI 官网上公开的数据集基本信息如表5 所示. 其中， 玻璃数据集根据其氧化物含量识别玻璃类型; 超声心电图用于对患者在心脏病发作后能否存活至少一年进行分类， 其属性是关于患者的一些检查结果; 肝炎数据集是基于一些肝功能测试结果去判断肝炎存不存在; 电离层数据集中包含有关雷达的数据; 鸢尾花数据集是在模式识别文献中使用相对广泛的数据库， 该数据集包含三个类别， 每个类别50 个实例， 其中每个类别指的是一种鸢尾花植物; 葡萄酒数据集是通过对每种葡萄酒的13 种成分进行分析， 从而确定葡萄酒种类; 脊椎数据集是通过人体脊椎不同位置的弯曲角度判断脊椎健康状态， 共有三个类别. 这七个数据集大小、属性各不相同且涉及不同的具体应用场景， 用于实验可以较全面地展现方法的有效性.

对比实验为四个著名的经典分类器SVM、SVM-RBF、REPTree、MP 和四种其他的基本概率赋值方法， 具体实验结果如表6 所示. 通过对表6 的结果分析可以看出， 本文所提的方法在不同应用场景、不同特征维度的数据集上， 整体准确率优于其他几种方法. 相较于其他的BPA 生成方法， 本文所提方法与分类器结果相比有一定优势， 而其他四种方法与分类器相比表现较为平均. 但本文所提方法在处理特征属性较多的数据时， 准确率会出现一定程度的下降， 如Hepatitis 和lono 数据集. 分析其主要原因为D-S 证据本身融合规则的弊端， 列属性偏多时对其逐个相乘会导致结果出现一定的误差. 由于本文主要研究BPA 生成方法， 并未对融合规则进行相应改进， 所以在此不予以讨论. 整体来看， 本文所提的基本概率赋值方法是有效可行的.

3.2 少样本数据下识别的有效性

针对脊椎数据集， 将三种类别的样本规模逐步增加. 考虑到该数据集三类样本数据数量不同， 且对样本量小于3 的极特殊情况不予以讨论， 因此构建密度模型的样本规模从3 增加到n， n 为类样本数量. 按照等步长递增， 最后一次参与实验的类样本数量为n， 划分30 个依次递增的样本规模， 将其由小到大逐个表示为k1，k2，…，k30. 随机选取对应于样本规模的数据样本作为模型训练集， 根据本文所提方法生成BPA， 将脊椎数据集总体样本作为测试集进行重复实验30 次. 对结果取平均值得到不同样本规模下的识别准确率， 具体结果如表7 所示. 由图4 可知， 本文所提方法在样本规模小于10 的极特殊情况下， 准确率也可以达到75%， 而且随着样本数的不断增加， 本文所提方法的识别率也随之有一定的提升.

4 结语

针对D-S 证据理论在分类应用中BPA 的生成问题， 本文提出结合近邻密度和信息修正的基本概率赋值生成方法， ①利用KNN 密度筛选样本的密度峰值构建特征模型值， 并基于模型值与样本的贴近度生成单焦元BPA， 通过不确定性与可信度对BPA 进行双重信息修正并对全子集事件赋值; ②通过在七个数据集上进行不同算法的准确率比较研究， 本文构建的BPA 生成模型准确性及鲁棒性相对SVM、SVM-RBF、REPTree、MP 和其他四种基本概率赋值方法均有一定优越性; 在不同样本规模上的实验结果表明， 本文所述方法对处理样本量较少或样本分布不均的应用场景有一定的实际意义.

参考文献：

[1] DEMPSTER A P. Upper and lower probabilities induced bya multivalued mapping[M]//YAGER R R， LIU L. ClassicWorks of the Dempster-Shafer Theory of Belief Functions.Berlin， Heidelberg： Springer， 2008.doi：10.1007/978-3-540-44792-4_3.

[2] SUN Y， LI C， LI G， et al. Gesture recognition based on kinectand sEMG signal fusion[J]. Mobile Networks and Applications，2018（23）： 797-805. doi：10.1007/s11036-018-1008-0.

[3] PAN Y， ZHANG L， LI Z W， et al. Improved fuzzy Bayesiannetwork-based risk analysis with interval-valued fuzzy setsand D – S evidence theory[J]. IEEE Transactions on FuzzySystems， 2019， 28（9）： 2063-2077. doi： 10.1109/TFUZZ.2019.2929024.

[4] 尹东亮， 黄晓颖， 吴艳杰， 等. 基于云模型和改进D-S 证据理论的目标识别决策方法[J]. 航空学报， 2021， 42（12）：299-310.

[5] 范晓建， 田建艳， 杨英波， 等. 基于改进D-S 证据理论的滚抛磨块融合决策模型[J]. 表面技术， 2021， 50（4）： 393-401.

[6] 林水生， 卫伯言， 杨海芬， 等. 引入新数据源的D-S 融合检测方法[J]. 电子科技大学学报， 2021， 50（6）： 861-867.

[7] 李伟， 周靖， 杜秀梅， 等. 基于D-S 证据信息融合方法的全地形车行驶工况辨识[J]. 重庆大学学报， 2022， 45（3）： 1-11.

[8] 潘伟豪， 徐赛博， 郭弘扬， 等. 基于D-S 证据理论的高分遥感影像建筑物变化检测[J]. 电子测量与仪器学报， 2022， 36（8）： 194-203.

[9] 李研芳， 黄影平. 基于激光雷达和相机融合的目标检测[J].电子测量技术， 2021， 44（5）： 112-117.

[10] 耿伊雯， 芮逸凡， 范路， 等. 基于D-S 证据多源信息融合与固态光电倍增-UHF 联合检测的GIS 局部放电模式识别[J/OL]. 绝缘材料， 2022，55（11）：109-117.

[11] 徐笑， 黄云志， 韩亮. 基于阵列旋转和改进证据理论的平面EMT 图像融合算法[J]. 仪器仪表学报， 2022， 43（10）：136-144.

[12] ZADEH L A. Fuzzy sets[J]. Information and Control， 1965， 8（3）： 338-353. doi：10.1016/S0019-9958（65）90241-X.

[13] 郭华伟， 施文康， 刘清坤， 等. 一种新的证据组合规则[J]. 上海交通大学学报， 2006（11）： 1895-1900. doi：10.16183/j.cnki.jsjtu.2006.11.018.

[14] QIAO J， ZHANG J， WANG Y. An improved multi-sensorD-S rule for conflict reassignment of failure rate of set[J]. SoftComputing， 2020（24）： 15179-15188. doi： 10.1007/s00500-020-05298-5.

[15] BOGLER P L. Shafer-dempster reasoning with applicationsto multi-sensor target identification systems[J]. IEEE Transac⁃tions on Systems， Man and Cybernetics， 1987， 17（6）： 968-977. doi：10.1109/TSMC.1987.6499307.

[16] 周剑， 马晨昊， 刘林峰， 等. 基于区间证据理论的多传感器数据融合水质判断方法[J]. 通信学报， 2016， 37（9）： 20-29.

[17] 丁腾辉， 冉志红， 林帆， 等. 基于改进的D-S 证据理论的桥梁监测数据融合研究[J]. 公路， 2022， 67（8）： 114-120.

[18] 韩崇昭， 韩德强， 介婧. 从生物感知认知到系统工程方法论[J]. 系统工程理论与实践， 2008， 28（Suppl）： 75-93.

[19] 康兵义， 李娅， 邓勇， 等. 基于区间数的基本概率指派生成方法及应用[J]. 电子学报， 2012， 40（6）： 1092–1096.

[20] WANG S， TANG Y. An improved approach for generationof a basic probability assignment in the evidence theory basedon Gaussian distribution[J]. Arabian Journal for Science andEngineering， 2022（47）： 1595-1607. doi： 10.1007/s13369-021-06011-w.

[21] 崔四芳， 宋慧啟， 李峰， 等. 基于PSO-BP 与D-S 证据的液压泵多源故障信号融合诊断[J]. 机械设计与研究， 2022， 38（2）： 155-157.

[22] 蒋雯， 陈运东， 汤潮， 等. 基于样本差异度的基本概率指派生成方法[J]. 控制与决策， 2015， 30（1）： 71-75.

[23] XU P， DENG Y， SU X， et al. A new method to determinebasic probability assignment from training data[J].Knowledge-Based Systems， 2013（46）： 69-80. doi： 10.1016/j.knosys.2013.03.005.

[24] 陈良臣， 傅德印. 面向小样本数据的机器学习方法研究综述[J]. 计算机工程， 2022， 48（11）： 1-13.

[25] GAO X， XIAO F. An improved belief χ2 divergence forDempster–Shafer theory and its applications in pattern recog⁃nition[J]. Computational and Applied Mathematics， 2022， 41（6）： 277. doi：10.1007/s40314-022-01975-3.

[26] XIAO F. Multi-sensor data fusion based on the belief divergencemeasure of evidences and the belief entropy[J]. InformationFusion， 2019（46）： 23-32. doi：10.1016/j.inffus.2018.04.003.

[27] DENG Y. Uncertainty measure in evidence theory[J]. Sci⁃ence China. Information Sciences， 2020（63）： 210201. doi：10.1007/s11432-020-3006-9.

[28] DENG Y. Deng entropy[J]. Chaos， Solitons amp; Fractals， 2016（91）： 549-553. doi：10.1016/j.chaos.2016.07.014.

【编校：王露】

基金项目：国家自然科学基金项目（61170060）; 安徽省重点教学研究项目（2020jyxm0458）