双粗糙元对高超音速边界层感受性的影响

史明方，徐立丹，唐小军，王振清

（1.内蒙古科技大学 土木工程学院，内蒙古 包头 014000；2.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；3.中国空间技术研究院 北京卫星制造厂有限公司，北京 100094）

高超音速武器以其优越的突防性能和损伤能力引起各国的重点关注［1］。在高超音速武器的设计过程中，高超音速边界层流动状态会直接影响高超音速武器的性能［2］，因为边界层层流转捩湍流会导致边界层内摩擦阻力和壁面加热显著增加。鉴于此，高超音速边界层的转捩控制是高超音速武器设计的关键技术之一。感受性是转捩的第1 个阶段，定义了边界层内扰动波的初始模态和幅值等参数。感受性阶段受到很多因素的影响，简单的可以分为来流扰动和壁面扰动［3］。其中来流扰动对感受性的影响研究较早，并已经取得了一系列的成果。

壁面粗糙元作为壁面扰动的重要组成部分，成为近些年的研究热点。在高超音速飞行器表面不可避免地存在壁面粗糙元，而壁面粗糙元又会对高超音速流场及边界层造成显著的影响，因此开展壁面粗糙元对边界层感受性作用机理的研究是十分必要的。董昊［4］总结了壁面粗糙元对高超音速边界层转捩的影响，指出壁面粗糙元对高超音速边界层感受性的作用机理十分复杂，包括壁面粗糙元和边界层内扰动波的相互作用，涉及瞬态增长和尾迹等现象。Saikishan 等［5］研究了壁面粗糙元造成的压力梯度对边界层转捩的影响。Clark 等［6］利用开源软件SU2 优化了涡流发生器的形状，以达到抑制边界层内Mack 模态演化的目的。壁面粗糙元可以依据相对光滑壁面的位置进行分类，在本文中，将高于光滑壁面的粗糙元称为K型粗糙元，相应的，将低于光滑壁面的粗糙元称为D 型粗糙元，K 型粗糙元的研究相对较早。段志伟等［7］分析了壁面粗糙元形状对转捩模式的影响。Ryota 等［8］结合fhf 直接数值模拟（direct numerical simulation，DNS）和非线性抛物化稳定性方程（nolinear parabolizd stability equations，NPSE）方法分析了三维圆柱状粗糙元高度对边界层转捩的影响，并讨论了边界层转捩时壁面粗糙元的临界高度。Vignes 等［9］分析了涡流发生器对圆柱形粗糙元周围高超音速流场气动特性的影响，发现涡流发生器有助于降低圆柱形粗糙元造成的气动阻力。D型粗糙元（主要集中在矩形腔结构）对高超音速边界层感受性的影响成为研究热点。李闯等［10］采用直接数值模拟方法讨论了空腔结构对6.0 Ma 高超音速边界层内扰动波演化的作用机理，发现空腔深度的增加会改变边界层内第2 模态的演化机理。刘俊等［11］系统地研究了空腔结构内波系的传播规律，讨论了压力振荡反馈模型的异同。李强等［12］利用激波风洞分析了展向凹槽对高超音速平板边界层转捩的影响，发现凹槽会促进转捩，并且随着凹槽深度和宽度的增加而增强。上述学者所分析的壁面粗糙元均为独立粗糙元，与之相对应的分布式粗糙元的研究在独立粗糙元的基础上也在逐步开展。董昊等［13］利用数值模拟和油膜干涉技术分析了壁面粗糙元高度和间距对转捩位置的影响，发现高度的影响要大于间距的影响。Irimpan 等［14］利用分布式粗糙元来表征烧蚀后的热防护系统，发现分布式粗糙元可以降低壁面加热率17%～42%。Zhou 等［15］指出波浪形壁面可以有效地抑制边界层内第2模态不稳定性，并且抑制效应随波浪形壁面的延长、加深和向下游移动而增强。Tong等［16-17］研究了正弦状壁面粗糙元对高超音速边界层转捩的影响。

目前，独立粗糙元和分布式粗糙元的研究都已取得了一定成果，但双粗糙元对高超音速边界层感受性影响的研究相对较少，并且大部分研究集中在分析双粗糙元间距的影响，缺乏双粗糙元组合类型影响的研究。本文对高超音速钝锥绕流流场进行直接数值模拟，讨论了双粗糙元组合类型对高超音速流场及边界层的影响；向流场中引入有效振幅脉冲慢声波，借助快速傅里叶变换方法分析了双粗糙元组合类型对脉冲慢声波作用下边界层内扰动波传播过程的影响，以揭示双粗糙元组合类型对高超音速边界层感受性的作用机理。

1 控制方程及数值方法

为了分析双粗糙元对脉冲有限振幅自由来流扰动作用下高超音速流场及边界层内流动及边界层的影响，本文采用直接数值模拟方法对高超音速流场进行直接数值模拟，揭示双粗糙元的组合类型对高超音速边界层感受性的影响。

对高超音速流场的数值模拟，控制方程为二维N-S方程：

式中：U为解向量；F和G为对流项；Eυ与Fυ为黏性项。解向量的具体表达式为：

对流项的表达式为：

黏性项的表达式为：

式中：ρ、u、v、T和p分别为密度、x方向速度、y方向速度、温度和压强；导热系数k可以通过假设普朗特数为常数获得；E为单位流体的总能，可以表示为单位流体的内能e与动能的和，具体为：

对于量热气体，气体内能e可计算为：

式中：比热比γ=1.4；τ为切应力，一般将空气看作牛顿流体：

式中μ为黏性系数，可以通过Sutherland公式获得：

式中：T0和μ0分别为参考温度和黏性系数；Ts=110.4 K。

本文考虑空气为完全气体，补充状态方程为：

式中：R为通用气体常数，R=286.94 J/(kg·K)。此外，本文将笛卡尔坐标系下控制方程进行坐标变换，转换到曲线坐标系下，以便于对复杂外形下的流场进行数值求解。

为了分析双壁面粗糙元组合形式对高超音速边界层感受性的影响，本文以自由来流扰动作用下高超音速钝锥绕流流场为研究对象，钝锥鼻部半径r=1 mm，半锥角θ=5°。本节以K型粗糙元（上游）和D型粗糙元（下游）的组合为例，给出了本文的计算模型及网格，计算网格分布为801×251，计算模型如图1 所示。K 型粗糙元（上游）和D 型粗糙元（下游）的双壁面粗糙元组合形式表示为Kf Db，下标f和b分别代表上游粗糙元和下游粗糙元，其余3 种组合形式以此类推。壁面粗糙元形状方程（以弧线ABCDE为例）为：

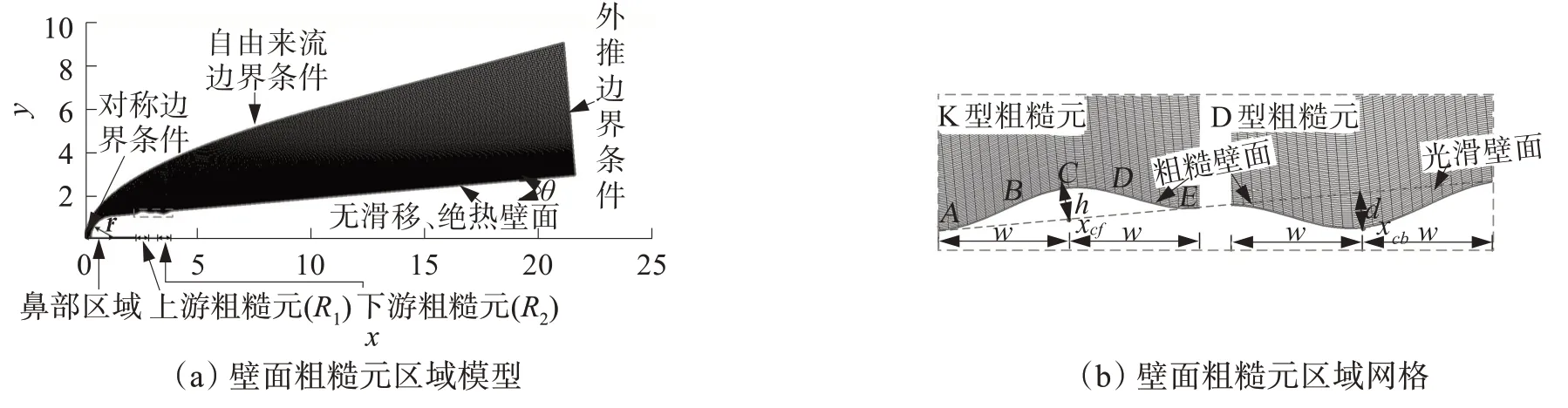
图1 计算模型及网格Fig.1 Computing model and grid

点A和点E分别为壁面粗糙元的起点和终点；点B和点D是壁面粗糙元形状的拐点(xⅠf或xⅠb和xⅡf或xⅡb)，分别称为第1拐点(xⅠf或xⅠb)和第2拐点(xⅡf或xⅡb)；点C为壁面粗糙元中点(xcf或xcb)。需要说明的是，K型粗糙元和D型粗糙元在同一位置处（壁面粗糙元中点相同）关于光滑壁面对称。计算模型的几何参数在表1中给出。本文使用的变量将分别利用头部半径r、来流参数ρ∞、u∞、T∞、p∞，u∞/r，r/u∞、k∞和μ∞对长度、密度、速度、温度、压强、频率、时间、导热系数和黏性系数进行无量纲化处理，自由来流条件在表2中给出。

表1 壁面粗糙元几何参数Table 1 Geometric parameters of roughness element mm

表2 自由来流条件Table 2 Conditions of freestream

自由来流参数，如扰动类型、持续时间等，会显著地改变高超音速边界层感受机理［18-19］。较大幅值的自由来流扰动与边界层的作用更加强烈，导致感受性阶段更复杂，甚至改变转捩路径。扰动波的作用时间也会显著地影响边界层感受性机理，短时间高强度的自由来流扰动又称为有限振幅脉冲扰动，对高超音速边界层感受性的影响机理与长时间低强度的自由来流扰动存在很大的差异。本文在分析壁面粗糙元对高超音速边界层感受性的影响时，向流场中引入脉冲慢声波扰动，其表达式为：

式中：ε、k和f分别为扰动波的幅值、波数和频率，ε=6×10-2,k=3.144 6×10-4和f=50π，因此本文自由来流扰动的周期为4。本文中扰动量是指非稳态高超音速流场的瞬时值与稳态流场值的差值，扰动量利用上标“'”表示，如温度扰动值利用“T'”表示。在分析壁面粗糙元对高超音速边界层感受性的作用机理时向高超音速流场引入脉冲扰动波，即向流场中引入半个周期(Δt=2)的脉冲慢声波扰动。

高阶精度有限差分方法可以稳定准确地对高超音速流场进行数值模拟。本文基于N-S方程采用S-W（steger-warming）通量矢量分裂方法将对流项分裂为正、负2 个流通量矢量。利用五阶加权本质无振荡（weighted essentially non-scillatory，WENO），格式对上述正、负流通量矢量进行离散；对于粘性项采用六阶精度中心差分格式进行离散；时间项利用三步三阶TVD 型Runge-Kutta 格式进行推进。本文采用的数值方法已经广泛使用在高超音速流场及边界层的数值模拟中［20-21］，并已对数值方法和网格独立性进行过验证，结果表明计算过程具有良好的稳定性，并可以保证计算结果的准确性。

2 双粗糙元对稳态高超音速流场的影响

壁面粗糙元会改变高超音速边界层感受性机理，为揭示双粗糙元对高超音速边界层感受性的影响，首先需对双粗糙元作用下稳态高超音速流场进行分析。图2 为壁面粗糙元作用下高超音速流场流向速度分布，可以看出壁面粗糙元显著地改变了流场结构，在流场中形成压缩波和膨胀波。独立K型粗糙元导致流场中形成压缩波-膨胀波-压缩波波系；而独立D 型粗糙元导致流场中形成膨胀波-压缩波-膨胀波波系。双粗糙元会导致流场中形成更复杂的波系，上游粗糙元造成的压缩波或膨胀波会与下游粗糙元造成的压缩波或膨胀波相“融合”，例如KfKb型粗糙元对导致流场中形成压缩波-膨胀波-压缩波-膨胀波-压缩波波系，Kf粗糙元造成的下游压缩波和Kb粗糙元造成的上游压缩波发生了融合；相似的，KfDb型粗糙元则在流场中形成了压缩波-膨胀波-压缩波-膨胀波波系。需要指出的是K型粗糙元形成的波系结构与Xue等［22］分析在前台阶对高超音速流场的影响是相似的，同时也指出前台阶对高超音速流动的影响局限在一定范围内。

图2 稳定高超音速流场流向速度云图Fig.2 Contours of velocity along x-axis in syeady hypersonic flowfield

壁面粗糙元对高超音速流场结构产生了一定影响，壁面粗糙元也会对高超音速边界层内流动状态的影响，图3 给出了壁面双粗糙元对稳态高超音速边界层内壁面压力的影响。可以看出壁面粗糙元对粗糙元附近壁面压力分布产生了显著的影响。以独立K 型粗糙元为例，壁面压力在K 型粗糙元前缘区域显著增加，在第1拐点处达到最大值，之后壁面压力沿流向方向逐渐减小至第2 拐点，在粗糙元中心恢复到光滑壁面水平。在第2拐点至壁面粗糙元后缘区域，壁面压力逐渐增加至光滑壁面状态。壁面压力的变化情况是由壁面曲率变化导致的，本文所采用的壁面粗糙元由3 次多项式控制，并且壁面粗糙元中点处与光滑壁面平行，因此在壁面曲率增大的区域壁面压力增加，并在壁面粗糙元中心处恢复到光滑壁面状态。D型粗糙元对壁面压力的影响情况相似。此外，壁面粗糙元的影响范围有限，仅局限在壁面粗糙元附近，并且K 型粗糙元的影响范围要大于D 型粗糙元。K 型粗糙元的出现导致其上游和下游区域的压强分布产生了变化，该现象在D 型粗糙元中并不明显。对于双粗糙元，虽然壁面粗糙元的影响范围有限，但本文中下游粗糙元均位于上游粗糙元的影响范围之内，因此在K 型粗糙元下游的壁面粗糙元区域的壁面压强均发生了一定程度的减小，而在D 型粗糙元下游的壁面粗糙元区域的壁面压强均发生了一定程度的增长。DfDb型粗糙元在除两粗糙元之间的区域内，壁面压强分布与独立粗糙元相同。

图3 高超音速边界层内壁面压力比较Fig.3 Comparisons of wall pressure in hypersonic bound‐ary layer

壁面摩擦系数表征了边界层内的剪切状态，并且壁面摩擦力会显著地影响高超音速飞行器的性能。鉴于此，对边界层内壁面摩擦系数进行分析是有必要的。图4给出了边界层内壁面摩擦系数沿流向的分布。计算结果表明壁面粗糙元显著地改变了边界层内的流动状态，在K型粗糙元的中心处，壁面摩擦系数到达极大值。这是因为对于稳态流场来说，边界层外边界的速度是相同的，因此壁面摩擦系数与边界层厚度呈反比。在边界层内粘性的作用下，K型粗糙元中心处边界层的厚度最薄，壁面摩擦系数达到极大值。同理，壁面摩擦系数在D型粗糙元的前缘和后远处达到极大值，在D型粗糙元中心处达到了极小值。当壁面摩擦系数小于零时，说明在区域内发生了回流，产生了流动分离。在本文中，独立K型粗糙元并未造成流动分离，而独立D型粗糙元均导致边界层流动分离。这说明D型粗糙元更容易导致流动的分离。在双粗糙元中包含D型粗糙元时，在D型粗糙元区域内边界层都发生了流动分离。

图4 高超音速边界层内壁面摩擦系数比较Fig.4 Comparisons of friction coefficient in hypersonic boundary layer

此外，KfKb型双粗糙元也造成了流动分离，流动分离发生在双粗糙元之间。因为在Kf粗糙元后缘下游至Kb粗糙元上游区域内，压力显著增加，逆压梯度很大，导致流动在该区域内发生分离。流动分离现象会显著地改变边界层内的流动结构，进而影响到边界层内的壁面摩擦力和热流密度。独立粗糙元导致壁面摩擦系数沿流向的减小值要超过增加值，也就是说壁面粗糙元可以起到减小阻力的作用。也有学者得出相似的结论，Brian等［23］指出分布式粗糙元可以在保持边界层内摩擦阻力基本不变的情况下稳定边界层内扰动波。因此合理地布置壁面粗糙元可以在一定程度上达到减阻，甚至降热的目的。结合Zhou 等［15］指出壁面粗糙元可以稳定边界层的作用，壁面粗糙元的合理布置对高超音速飞行器的设计具有一定的指导意义。因此，对双粗糙元作用下高超音速边界层感受性机理的研究是有意义的。

3 双粗糙元对非稳态高超音速流场的影响

为了分析双粗糙元对高超音速边界层感受性的影响，向高超音速流场中引入脉冲慢声波扰动。图5 以KfKb型粗糙元为例给出了脉冲扰动波在高超音速流场中的传播过程。

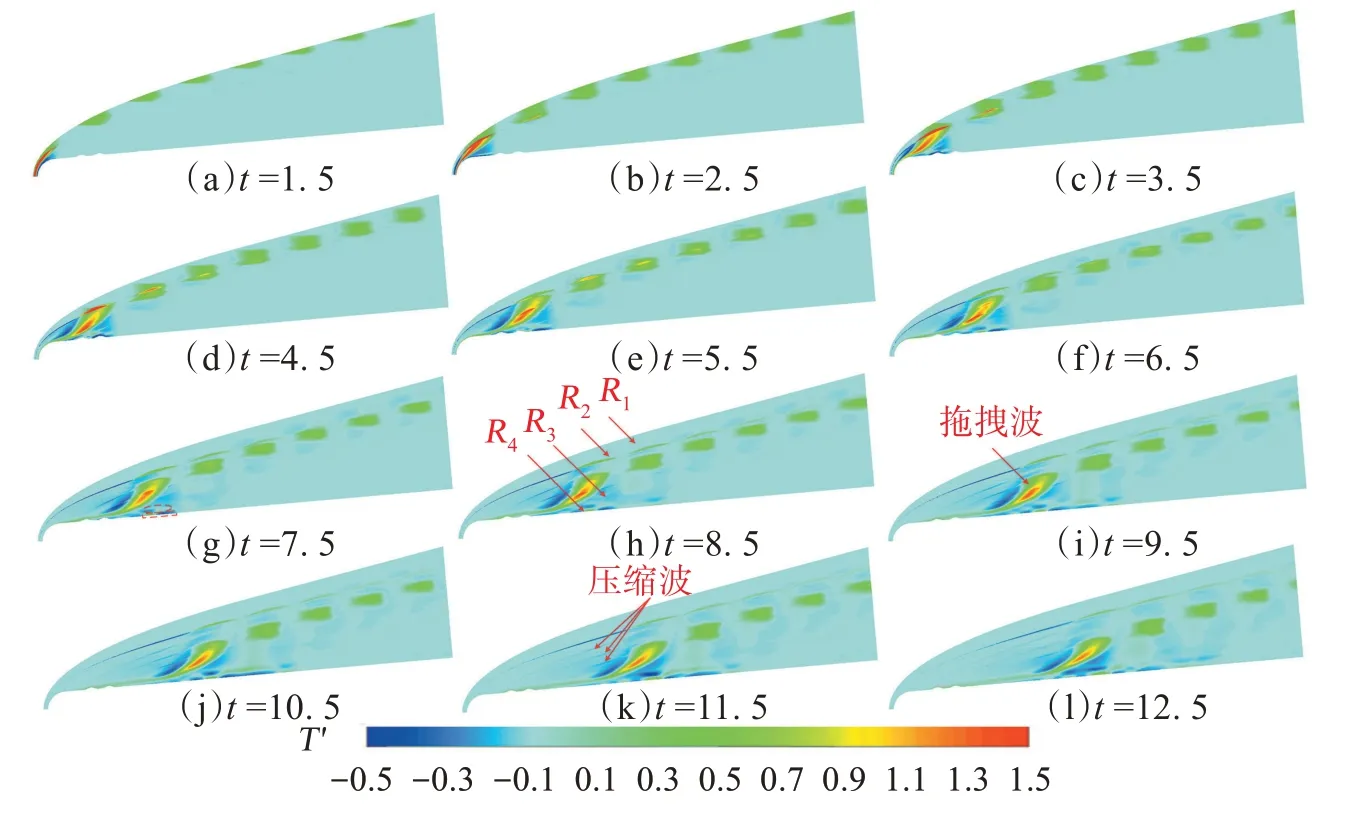
图5 脉冲扰动作用下高超音速温度扰动流场Fig.5 Contours of transient temperature fluctuation at different time

高超音速流场可以分为4 个区域：R1区域-激波外区域；R2区域-激波区域；R3区域-边界层与激波之间的区域；R4区域-边界层区域，如图5(h)所示。脉冲扰动波与弓形激波的作用更加强烈，在脉冲慢声波经过弓形激波后会在高超音速流场中形成“拖拽波”，拖拽波的形成是因为脉冲慢声波在经过激波后的速度不同。脉冲慢声波在与斜激波相互作用时，并未在流场中形成明显的拖拽波，而是在流场中依次形成低温-高温结构。壁面粗糙元影响了脉冲慢声波在高超音速流场中R3和R4区域的传播。

第2 节已经指出壁面粗糙元改变了稳态高超音速流场结构，在流场中形成一组新的波系，并导致边界层发生流动分离。可以看出双粗糙元造成的压缩波和膨胀波波系改变了R3区域内扰动波的传播，在流场中明显的看出3道压缩波对流场内扰动波的放大作用，如图5(k)所示。自由来流扰动在经过KfKb型粗糙元造成的压缩波时被放大，并在离开这3道压缩波时恢复到光滑壁面状态。脉冲慢声波在经过激波后进入到边界层内，激发出边界层内扰动波，导致边界层内依次形成了低温斑和高温斑结构，如图5(g)中矩形区域所示。边界层外边界处形成“绳索”状高温斑-低温斑结构，如图5(g)中椭圆形区域所示，Ma等［24-26］指出这是边界层内慢声波结构的典型结构。边界层内扰动波在向下游传播的过程中逐渐耗散，但在边界层内形成残余反射波，反射波在边界层内进行多次反射，最终在边界层内粘性作用下耗散掉，如图5（l）所示。

为了更清晰地揭示壁面粗糙元对高超音速边界层感受性的影响，图6给出了边界层内不同位置处壁面压强扰动值随时间的变化情况。边界层内越下游区域越晚感受到边界层内扰动波，扰动波在向下游传播过程中，持续时间越长，在x=0.90 处，扰动波持续时间Δt=3.8；而在x=18.89 处，扰动波持续时间Δt=17.9。边界层内扰动波持续时间都超过了自由来流扰动波的时间(Δt=0.5T=2)。说明边界层内反射波在边界层内多次反射后才逐渐耗散消失。此外，扰动波向下游传播过程中幅值逐渐减小，扰动波波形越复杂。边界层内扰动波在进入到高超音速流场后呈现“正弦波”分布，在向下游传播的过程中，在粘性的作用下，扰动波的幅值逐渐减小，波形逐渐变得复杂。边界层内扰动波在通过第1粗糙元(Kf或Df)时，边界层内扰动波在通过Kf粗糙元前缘(x=0.90)处被放大，而Df粗糙元前缘处壁面压强扰动并未受到影响，因为D 型粗糙元的影响范围较小。在Kf粗糙元中点(x=1.39)处，边界层内扰动波稍被放大。边界层扰动波在通过第1粗糙元后缘(x=1.79)处，Kf、Kf Kb和Kf Db粗糙元降低了该处边界层扰动波的幅值，而Df、Df Db和Df Kb粗糙元放大了该处扰动波的幅值。Kb粗糙元也放大了扰动波的幅值，但Db粗糙元并未对该处产生影响。在两粗糙元中点(x=1.91)处，Kf和Db粗糙元抑制了边界层内扰动波的传播，因此，Kf Db粗糙元对边界层内扰动波传播的抑制作用更明显。同理，Df和Kb粗糙元促进了边界层内扰动波的传播，因此，Df Kb粗糙元对边界层内扰动波传播的促进作用更明显。Kf Kb和Df Db双粗糙元对该点扰动波的传播基本没影响，这可以说明同类型的上游粗糙元和下游粗糙元对两粗糙元中点处的影响是相同的，二者的影响相互抵消。下游粗糙元对边界层内扰动波的作用机理与上游粗糙元相同，这里不再赘述。壁面粗糙元影响的局限性导致在两粗糙元下游区域的扰动波的传播并未受到影响。

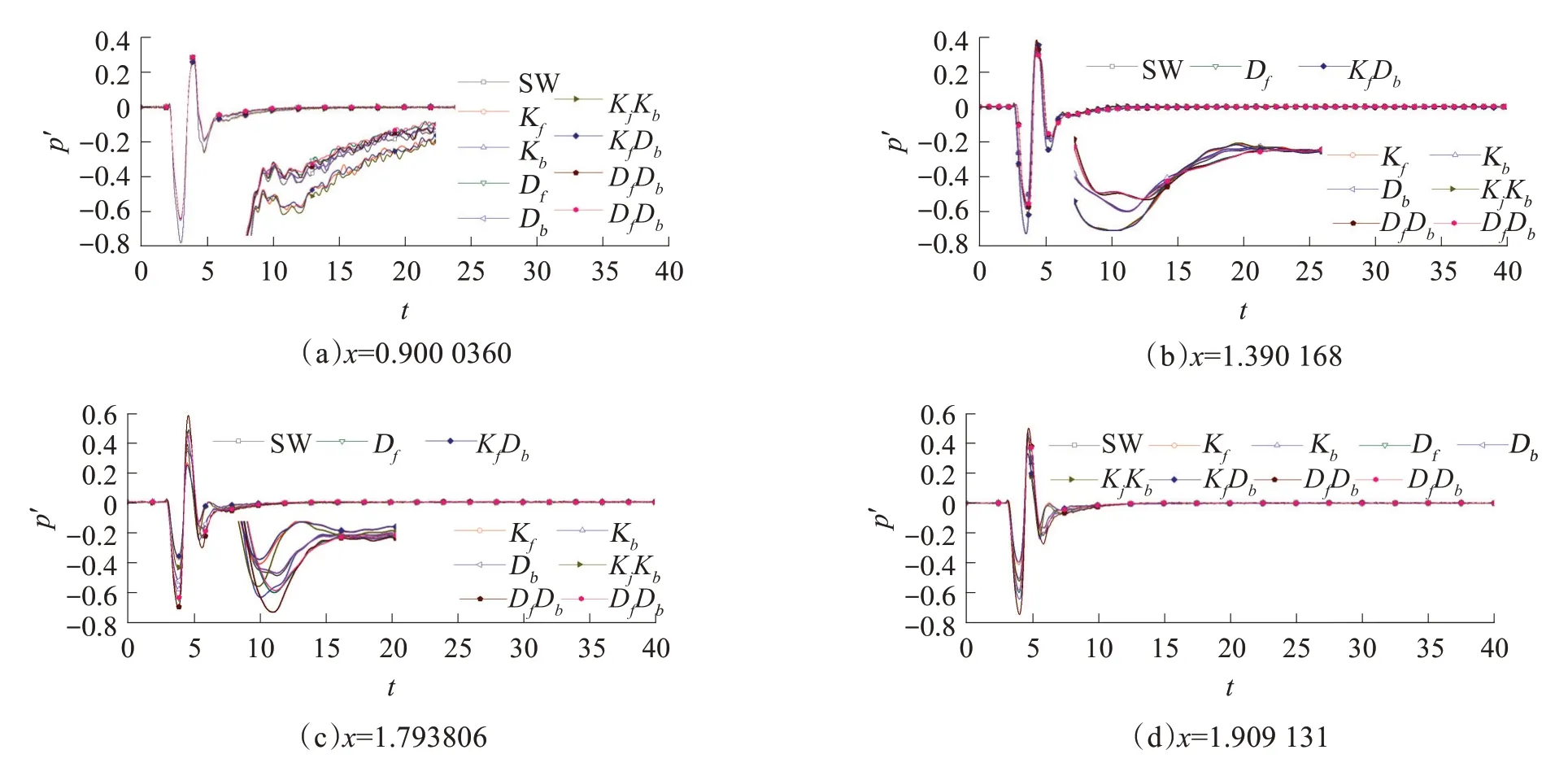
图6 各流向位置处壁面压强扰动幅值-时间对比Fig.6 Time history trace of wall pressure fluctuation at various streamwise locations

为了更准确地分析高超音速边界层内扰动波的传播过程，本文采用快速傅里叶变换方法将边界层内的时域信号转换到频域内，以分析边界层内不同模态扰动波的演化过程。快速傅里叶变换公式为：

式中：f为自由来流扰动波的频率；|p'|为任意瞬时压力扰动；|p'n|和φn分别为局部扰动幅值和相角，下标整数n代表了扰动场的波模态，当n=0代表平均流场变形，n=1代表基频扰动，n=2代表二阶谐频扰动，以此类推。第2节已经指出壁面粗糙元对高超音速流场的影响具有局限性，因此本节仅给出x=0.90～10.01范围内边界层内扰动波的演化情况，如图7所示。可以看出边界层内扰动波在向下游传播过程中扰动波的波形变得越来越复杂，扰动波的幅值在逐渐减小，在x=10.01处稍有增加。此外，边界层内扰动波的主导模态在逐渐增大，如在x=0.90处，主导模态f=0.033；在x=1.79处，主导模态f=0.028；在x=2.40处，主导模态f=0.025，并且主导模态在边界层内扰动波所占比例在逐渐减小。也就是说高超音速边界层内扰动波存在模态竞争现象，主导模态进行了模态迁移。

图7 边界层内扰动波频率振幅Fig.7 Frequency-amplitude diagram of perturbations in boundary layer

壁面粗糙元对边界层内不同模态扰动波传播过程的影响相同，即在K 型粗糙元前缘区域和D 型粗糙元的后缘区域内，边界层内扰动波的幅值被放大；相应的在D型粗糙元前缘区域和K型粗糙元的后缘区域内，边界层内扰动波的传播被抑制。值得注意的是Kf独立粗糙元抑制了其下游区域内扰动的演化。双粗糙元的组合类型对边界层内不同模态扰动波的传播具有一定的影响，Kf Kb型双粗糙元导致壁面粗糙元下游区域内扰动波的主导模态显著降低，而且这种抑制效应还要强于Kf独立粗糙元。下游的Kb粗糙元增强了上游的Kf粗糙元对Kf Kb双粗糙元下游边界层内扰动波的抑制效应。这就证明了K型粗糙元对下游的边界层内扰动波演化的抑制具有协同效应。

4 结论

1）双壁面粗糙元会显著地改变稳态高超音速流场及边界层内的流动状态，导致流场中形成一组新的波系，并导致边界层内出现流动分离。如Kf Kb型粗糙元会导致流场中形成压缩波-膨胀波-压缩波-膨胀波-压缩波波系，并在两粗糙元之间形成流动分离。

2）双壁面粗糙元导致流场中形成新的波系显著地影响了高超音速流场中自由来流扰动的传播过程，使扰动波在压缩波作用下发生了一定的变形；当自由来流扰动离开壁面粗糙元造成的波系后，新的波系影响也随之消失。

3）双壁面粗糙元也改变了边界层内扰动波的演化过程，在K 型粗糙元前缘区域和D 型粗糙元的后缘区域内，边界层内扰动波的幅值被放大；在D型粗糙元前缘区域和K 型粗糙元的后缘区域内，边界层内扰动波的传播被抑制。壁面粗糙元对边界层内扰动波的作用也局限在一定范围内。

4）边界层内扰动波在向下游传播过程中主导模态在逐渐减小，并存在模态竞争现象。双粗糙元的组合类型对边界层内不同模态扰动波的传播具有一定的影响。其中，KfKb型双粗糙元显著抑制了其下游区域内主导模态扰动波的演化，并且2个K型粗糙元对其下游边界层内扰动波演化的抑制具有协同效应。