滑落式救生艇入水阶段运动响应数值预报研究

凌宏杰，钱进，王志东，徐峰

（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

随着国家海洋战略的推进实施以及国际航运事业的迅猛发展，船舶上的人员安全问题越来越受到各国海事组织的高度重视，救生艇及其释放装置已成为国际海上人命安全公约强制要求配备的海上救生设备。将自由滑落式救生艇安放于船艉，由艇内操作人员打开释放钩即可完成释放，具有操作简单、安全性高、降落速度快的优点。因此，自由滑落式救生艇已成为国际上最为安全的船舶救生撤离系统，对于保障海上人员生命安全意义重大［1］。

救生艇从空气中进入水中后，周围介质的突变会引起结构物表面及内部空间产生剧烈的冲击载荷，同时物体与流场之间的相互作用对其运动姿态与入水速度产生影响，因此救生艇入水阶段的运动响应变得异常复杂。自Von［2］的开创性研究以来，研究者采用多种方法研究结构物入水问题。马庆鹏等［3］采用流体体积法多相流模型，引入重叠网格技术分析了锥头圆柱体入水后速度及入水空泡形态的发展规律；Wei等［4］实验研究了三维圆柱体的平移运动和旋转运动规律；王海洋［5］基于建立的重叠网格数值计算方法，分析了初始运动参数对导弹尾罩入水过程的流场特性、运动特性和流体动力特性的影响；Jiang 等［6］试验研究了弹丸体入水过程近水面空腔的流动特性，Gao 等［7］通过求解雷诺平均纳维-斯托克斯方程和六自由度刚体运动方程，研究了高速圆柱弹丸体斜向入水的主要特征。Shentu［8］基于浸湿边界法（boundary data immersion method,BDIM）和流体体积法（volume of fluid method，VOF）分析疏水性物体的入水运动轨迹引起的空腔形状；Cheng［9］采用光滑粒子（smoothed particle hydrodynamics,SPH）方法对船艏入水三维模拟，研究了冲击载荷的变化特征、流动分离以及喷雾射流现象。Xie 等［10］利用模型试验研究船艏入水运动响应以及瞬态砰击等具有强非线性特征的流固耦合现象；余德磊等［11］研究了不同参数下并联运动体的空泡形态及特征尺寸变化、侧向与偏航运动规律。

本文针对滑落式救生艇入水阶段运动响应问题，基于粘性流体理论，建立了一套救生艇入水运动响应数值预报方法，开展了不同垂向初速度、水平初速度和入水角度对救生艇入水运动响应的影响，定量分析了初始条件对救生艇入水垂向和水平加速度及入水深度等参数的影响。

1 救生艇模型建立与计算方法

1.1 救生艇模型及网格划分

选取某一封闭式救生艇为研究对象，救生艇三维模型和主尺度分别如图1，救生艇总长12.5 m，高度4.2 m，型宽5.5 m，空艇重12 850 kg，满载总重37 650 kg。为了节约计算资源、提高计算效率，将救生艇距离液面以上H0=0.5 m 作为入水砰击载荷计算的初始位置，以此时刻抛落速度视为入水初速度。设置初速度及初始纵摇角模拟入水前空中抛落末状态。采用重叠网格技术分别建立嵌套域与背景域，其中嵌套域为3L×2L×2L，背景域为8L×8L×5.5L，L为艇长，计算域网格划分见图2。为了捕获砰击发生、射流和自由液面变形现象，在砰击发生区域、自由液面附近和艇体可能的运动范围处进行网格加密处理，保证嵌套域与背景域在数值插值的地方网格尽量尺寸一致。全局网格数量为910 万，网格最小夹角为23.28°，正交性良好。

图1 救生艇三维模型Fig.1 Three dimensional model of lifeboat

图2 救生艇计算模型网格划分Fig.2 Lifeboat calculation model meshing

1.2 计算工况

滑落式救生艇入水分为轨道滑行、空中自由落体、砰击入水和上浮4 个阶段［12］。入水阶段作为滑落式救生艇入水全过程中最复杂的一个阶段，涉及到固液耦合、自由液面变形等复杂水动力学问题。采用空中自由落体阶段计算结果作为入水阶段的初始条件，保证救生艇入水全过程运动中动能的连续性。本文制定了数值计算工况表（见表1）。表1 中工况A1～A6、B1～B3、C1～C6分别用于探讨不同垂向初速度、水平初速度和不同入水角对救生艇入水阶段运动性能的影响。图3给出了滑落式救生艇入水前的初始状态示意图，水平向右为x正方向，垂直于水面向上为z轴正方向，坐标系满足右手系，艇体中轴线与自由面夹角为纵倾角θ，艇艏最低点距离自由面初始高度H0=0.5 m。

表1 入水运动计算工况表Table 1 Working condition table of water entry movement calculation

图3 滑落式救生艇入水前的初始状态示意Fig.3 Schematic diagram of the initial state of the slidedown lifeboat before entering the water

1.3 计算参数设置

基于粘性流体理论的滑落式救生艇三自由度入水运动响应数值计算的参数设置如下。

1）三维非定常双相流；压力速度耦合求解算法；动量方程采用中心差分格式离散；

2）选用k-ω（SST-Menter）湍流模型，k与ω的值与雷诺数有关；湍流方程采用中心差分格式离散；自由面采用混合自由面捕捉与重构相结合格式离散；

3）艇体表面均采用标准壁面函数，嵌套域外边界采用重叠条件，背景域上下重力方向边界设为指定压力，其他边界设为远场条件；

4）耦合求解前进、垂荡、纵摇3 个自由度，约束另外3个自由度；整个计算采用非定常条件，时间步长Δt=0.000 1 s 保证高精度捕捉艇体入水瞬态过程的运动。

2 计算结果与分析

文中数据为监测艇体重心处的加速度、速度和位移等参数；艇体运动轨迹z值以自由面位置为零点，最大入水深度为运动轨迹最低点为准。

2.1 初始垂向速度对救生艇入水运动影响分析

图4给出了不同初始垂向速度下救生艇入水过程中垂向加速度和速度时历曲线。从图4中可以看出：

图4 不同初始垂向速度下救生艇垂向加速度与速度时历曲线Fig.4 Vertical acceleration and velocity time history curves of lifeboats at different initial vertical velocities

1）艇体接触自由液面前，主要受重力、空气阻力作用的影响，经短暂加速后与水面接触，出现砰击现象，加速度迅速增至最高值，峰值达25.9g，压力释放后，出现快速衰减现象，随着艇体快速入水对水体的高速挤压，间隔约0.08 s 后会出现二次峰值，释放艇体压力后，经过二次减速后，艇体运动速度大幅下降，加速度趋于缓和直至达到平衡状态。

2）垂向加速度随着初始垂向速度增加而增加，救生艇入水瞬间加速度越大产生的冲击力越大；垂向速度从20～35 m/s对应的峰值加速度分别为8.7、12.7、16.2、19.1、20.3、25.9g；当vz≤29 m/s 时，加速度斜率约为1.1g；当vz≥32 m/s时，加速度斜率约为1.8g；当29 m/s＜vz＜32 m/s时，加速度处于转捩区。

图5给出了不同初始垂向速度下救生艇入水过程中水平加速度和速度时历曲线。从图5中可以看出：

图5 不同初始垂向速度下救生艇水平加速度与速度时历曲线Fig.5 Lifeboat horizontal acceleration and speed time history curves at different initial vertical speeds

1）艇体与水面接触前，水平方向不产生加速度；当艇体与水面接触时，艇体艏部下缘产生高压区，艇体产生作用力在水平方向产生一个分量，使艇体产生一个前冲的加速度，进而出现向前的加速运动现象，该作用力为瞬态作用载荷（0.2 s 内完成整个作用过程），与垂向加速度具有同步性，艇体前冲运动中受到水动阻力作用，速度不断减小。瞬态作用载荷产生的水平加速度最大值达6g。

2）水平加速度随着初始垂向速度增加而增加，初始垂向速度从20～35 m/s 对应的水平加速度峰值分别为1.86、2.74、3.41、4.02、4.93、6.0g，近似满足线性关系，斜率约为0.265g；救生艇前冲速度越大，有助于救生艇快速远离母船。

图6给出了不同垂向速度下救生艇入水运动轨迹和纵倾角时历曲线。从图6中可以看出：

图6 不同初始垂向速度下救生艇入水运动轨迹和纵倾角时历曲线Fig.6 Time history curves of the lifeboat entering the water trajectory and trim angle at different initial vertical speeds

1）从艇体艏部接触到自由液面至最大入水深度所需时间约0.7 s（结合图4（b））；不同初始垂向速度下艇体的入水阶段运动轨迹具有相似性；入水深度和前冲距离随着垂向速度的增加而增加。当vz=35 m/s时，最大入水深度为He=7.26 m，此刻前冲距离为9 m。

2）当艇体艏部与水面接触时，出现砰击现象，产生较大抬艏力矩，使艇体迅速从埋艏转化为抬艏所需时间小于0.5 s；纵倾角变化率随初始垂向速度增加而增加。

综上所述，救生艇入水阶段的水平、垂向加速度及纵倾角变化率与初始垂向速度关系密切；由于人员承受瞬时极限加速度为20g，因此初始垂向速度不超过29 m/s。不同初始垂向速度救生艇入水深度和加速度峰值统计值详见表2。

表2 不同初始垂向速度下救生艇入水深度和加速度峰值统计值Table 2 Statistics of lifeboat penetration depth and peak acceleration at different initial vertical velocities

2.2 初始水平速度对救生艇入水运动影响分析

图7～9给出不同初始水平速度下救生艇垂向和水平向加速度和速度时历曲线及运动轨迹与入水纵倾角时历曲线，从图7～9中可以看出，3个初始水平速度下，各条曲线处于重合状态，表明初始水平速度对垂向和水平加速度、入水深度、入水纵倾角的影响不大。

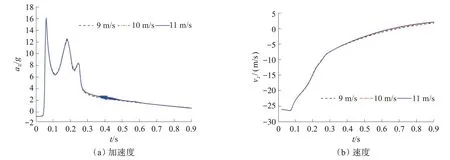
图7 不同初始水平速度下救生艇垂向加速度与速度时历曲线Fig.7 Vertical acceleration and velocity time history curves of lifeboats at different initial horizontal velocities

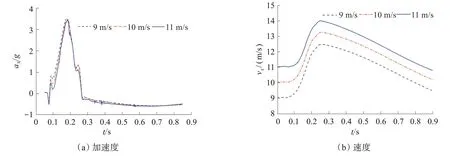
图8 不同初始水平速度下救生艇水平加速度与速度时历曲线Fig.8 Lifeboat horizontal acceleration and speed time history curves at different initial horizontal speeds

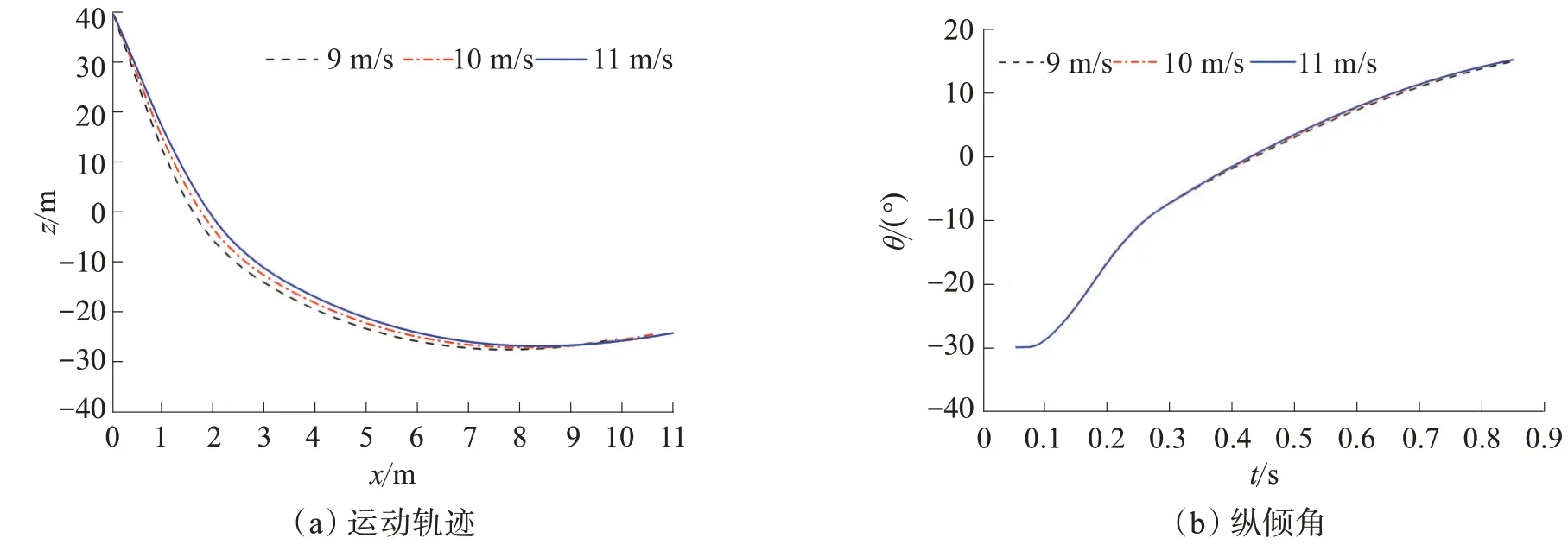
图9 不同初始水平速度下救生艇入水运动轨迹和纵倾角时历曲线Fig.9 Time history curve of the lifeboat entering the water trajectory and trim angle at different initial horizontal speeds

2.3 初始纵倾角对救生艇入水运动影响分析

图10给出了不同初始纵倾角下救生艇入水过程中垂向加速度和速度时历曲线。从图10中可以看出：

图10 不同初始纵倾角下救生艇垂向加速度与速度时历曲线Fig.10 Time-history curves of vertical acceleration and velocity of lifeboats under different initial trim angles

1）艇体不同初始纵倾角入水加速度均出现2次峰值，对应艇体受到2次压力峰值，随着纵倾角的增加，出现第2 次压力峰值的时间后移，且趋于平缓；艇体与水体的接触面随着初始纵倾角的增加而减小，艇体受到水体的水动压力随之减弱，因此出现峰值压力减小现象；艇体入水后，随着初始纵倾角的增加，艇体垂向速度衰减速率减小。

2）垂向加速度随着初始纵倾角增加而减小，初始纵倾角θ从30°～60°对应的峰值加速度分别为16.2、14.7、12.3、11.3、10.9、10.8g和10.7g；当θ≤45°时，加速度斜率约为-0.342g；当θ≥50°时，加速度趋于稳定；当45°＜θ＜50°时，加速度处于转捩区。

图11给出了不同初始纵倾角下救生艇入水过程中水平加速度和速度时历曲线。从图11中可以看出：

图11 不同初始纵倾角下救生艇水平加速度与速度时历曲线Fig.11 Time history curves of horizontal acceleration and velocity of lifeboats at different initial trim angles

1）随着艇体初始纵倾角的增加，艇体艏部与水体接触时，顶部区域面积不断增加，而艏部底部面积减小，水动压力作用于艏部底部面积产生前冲力，而作用于顶部区域产生反冲力，因此入水前期艇体水平加速度出现反冲现象，且随着纵倾角的增加而增加，作用时间极短约为0.1 s；随着时间推移，艇体入水深度增加和纵倾角快速增加，改变艇体的姿态，艇体受到的水动压力合力表现为前冲力，艇体沿水平加速运动，作用时间约为0.4 s；最后前冲运动中艇体受到水动阻力作用，速度不断减小。当θ=30°时，瞬态作用载荷产生的水平加速度最大值达3.41g。

2）水平加速度随着初始纵倾角增加而较小，初始纵倾角θ从30°～60°对应的峰值加速度分别为3.41、3.39、3.35、3.20、3.10、2.63g和2.02g，当θ≤45°时，加速度变化不大；当θ≥50°时，加速度斜率约为-0.108g；当45°＜θ＜50°时，水平加速度处于转捩区。

图12 给出了不同初始纵倾角下救生艇入水运动轨迹和纵倾角时历曲线。从图12中可以看出：

图12 不同初始纵倾角下救生艇入水运动轨迹和纵倾角时历曲线Fig.12 Trajectory of the lifeboat entering the water and the time history curve of the trim angle under different initial trim angles

1）不同初始纵倾角下艇体的入水阶段运动轨迹具有相似性；入水深度随着初始纵倾角的增加而增加。当θ=60°时，最大入水深度为He=7.35 m，此刻前冲距离为8 m。

2）不同初始纵倾角下艇体的入水阶段纵倾角变化具有相似性；艇体达到水平姿态所需时间随着初始纵倾角的增加而增加。

综上所述，救生艇入水阶段的水平、垂向加速度及纵倾角变化率与初始纵倾角关系密切；从人员安全和快速逃离的角度出发，初始纵倾角应不超过45°。不同初始纵倾角救生艇入水深度和加速度峰值统计值详见表3，初始水平速度vx为10 m/s，垂向速度vy为26 m/s。

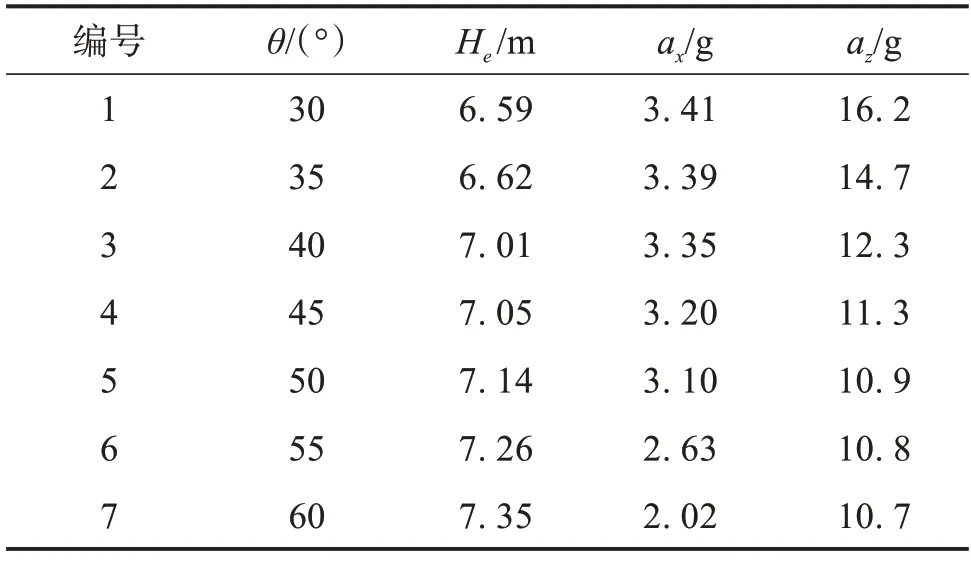
表3 不同初始纵倾角下救生艇入水深度和加速度峰值统计值Table 3 Statistics of lifeboat penetration depth and peak acceleration at different initial trim angles

3 结论

1）救生艇入水前的垂向速度和纵倾角对其入水阶段的加速度、入水深度和前冲距离影响较大，而水平速度影响较小，可忽略不计；

2）救生艇入水纵倾角不超过45°，有助于增加救生艇前冲距离，提高其快速逃离能力。

3) 救生艇入水垂向速度与加速度关系密切，可通过降低救生艇垂向速度，有效降低其入水加速度，提高人员安全性。