基于直线检测算法的矢量波导不变量估计

莫世奇，王博，李韬哲

（1.哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001；3.杭州应用声学研究所，浙江 杭州 310000）

海洋波导的重要特点是在低频声场中存在稳定可观测的干涉结构［1-3］，Kuperman［4］认为近代水声学以及水声信号处理的主要研究方向就是海洋波导中低频声场的干涉结构，随着矢量水听器技术的蓬勃发展，声场中的振速信号受到越来越多人的关注，越来越多的水声工作者投入到对声压信号和振速信号联合处理方法的研究上，共同促使声场干涉结构逐渐成为国内外水声研究的重点。

对声场干涉结构研究的另一个里程碑式的节点是波导不变量理论的提出，通过波导不变量描述海洋波导中的干涉条纹［5-6］，波导不变量的分布情况与波导环境、模态阶数有关，反映到干涉图像上就是其干涉条纹的斜率变化［7］，因此需要借助图像处理技术提取干涉图中干涉条纹的信息。

用于干涉条纹提取的较为常见的图像处理算法为Hough变换和Radon变换［8-10］，二者的原理都是将像素从图像空间映射到参数空间，这2 种变换的提取效果普遍受遍历角度步长设置的影响较大，特别是想区分多条斜率相近的直线时，对遍历角度的步长要求更加严格，会导致需要一个非常庞大的参数空间去承载变换后的结果，而在图像空间中的信息较少时，在参数空间很难形成比较尖锐的峰值。而Hough变换的下一步操作就是通过设置阈值将符合门限要求的点定义为直线，如果无法累积出足量像素点，很容易发生漏检。同时，由于空间变换类算法都需要对整个图像空间进行处理再累积，其处理速度会受图像空间大小的影响，而且结果必然是表征图像空间的整体特性，无法分别表征图像空间中各条直线的特征。此外，Hough 变换要求输入为二值图像，所以在提取干涉条纹斜率前需要对图像进行二值化操作，而且二值化精度对于变换最终结果影响较大；Radon 变换是依靠线积分实现的，虽然不要求输入为二值化矩阵，但是输出结果会受输入图像像素点密度分布影响，而且如果直线结构的强度分布不均匀，其提取结果也将不准确。

因此需要寻找其他算法进行干涉条纹提取。直线检测（line segmen detection,LSD）算法由von 等［11］提出。从图像梯度角度入手，经过精细化处理就能够得到一条线段。它具有不需要额外的参数输入、能够控制自身的误检数、在较短时间内获得较高精度的直线段检测结果等优点。本文提出利用LSD处理算法进行矢量声场干涉条纹的提取，并对典型浅海环境声场的波导不变量进行估计，仿真分析表明LSD直线检测算法的检测效果令人满意。

1 矢量声场和波导不变量理论

1.1 矢量声场干涉结构

理想流体介质中声矢量场涵盖质点位移re-iωt、质点振速ve-iωt、质点加速度ae-iωt等，对于谐和波场，它们之间可以相互导出。声波传播过程必然伴随能量的传递，分析声场能量的干涉特性，从声压谱入手，根据简正波理论［12-13］，得到柱坐标系下声压谱密度函数为：

式中：Δknm(ω)=krn(ω)-krm(ω)为第n阶与第m阶简正波水平波数差；p(r,z,ω)=为有限阶简正波和的形式下，声场中某点声压的表达式，声压谱即为此点声压与其共轭复数的乘积。

在平面波情况下，分层介质中的动能谱密度和势能谱密度相等，声强与声能量密度在水平方向上可看作正比关系，所以声压谱的干涉特性可以推广到振速谱中。

振速自谱为：

式中：第1部分为各阶模态自身作用的非相干项；第2 部分为模态间的相干项，引起谱强度振荡变化，直接导致明暗相间条纹的形成。

1.2 波导不变量表征干涉条纹方程

简正波的相互干涉，浅海波导中的声场会形成稳定的条纹结构，在其距离-频率平面上，如果Δr≪r0，Δω≪ω0，r0和ω0分别为中心距离和中心频率，可认为在此干涉条纹上声强不变，则其全微分为0，可以表示为：

式(2)转化为：

式中vp和vg分别为水平相速度和群速度。

干涉条纹的斜率与声源距离、频率之间的关系用一个参数——波导不变量β来描述，其表达式为：

由式(3)可以求过宽带声源距离-频率域中某点(r0,ω0)的干涉条纹方程为：

即：

可见，干涉条纹上频点与距离的β次方有关，当波导不变量β ≈1 时，此式描述为一族经过频点0 的直线方程。

2 矢量声场干涉条纹提取

2.1 矢量声场干涉结构融合

声压谱和水平振速自谱的干涉条纹虽然在谱强度上存在差异，但是都存在稳定的干涉结构，且条纹具有一致性。声压和振速在时空上具有相关性，不同频率及位置处的干涉条纹强度不同，信息上具有互补性，采用图像融合能在声压、振速干涉结构中相关信息最大合并的基础上减少输出的不确定度和冗余度，扩大干涉图所含有的时间-空间信息，减少不确定性，增加可靠性，使融合后的干涉图对声场干涉结构会有更全面、清晰的描述，从而更有利于干涉条纹的提取。

本文从数据级图像融合入手，并以图像的标准差、平均梯度和平均空间频率为标准，对图像融合结果进行评价。标准差反映图像内像素点的离散程度，数值越大表明图像质量越优良，平均梯度和空间频率反映图像的清晰度，数值越大表示图像越清晰。

选择基于小波变换的图像融合方法，将图像分解为4 层，对各分解层从高到低分别进行融合。常规的融合方式为在高频部分采用加权平均法或基于区域能量的融合准则等方法进行融合，在低频部分采用平均的线性融合方法。但是在许多情况下，单用取平均的方法会影响最终的融合效果，所以本文采用平均与选择相结合的融合规则，融合结果如表1所示。

表1 融合结果Table 1 Fusion results

将2 幅图像的相关性作为选择融合方式的标准时，设定2 幅图像的相似程度系数，当2 幅图像相关性程度较强时，即认为2幅图像的能量相差不大，此时低频部分采用平均的线性融合方法，高频部分采用加权平均法；当2幅图像相关性程度较弱时，则认为2 幅图像局部能量相差较大，此时低频部分仍然采用平均的线性融合方法，高频部分基于区域能量的融合准则，选取局部区域能量较大的小波系数作为融合图像的小波系数。

从融合结果的评价指标中可以看出，将2 幅不同质量的图像进行融合后，平均与选择相结合的融合方法可以保持图像的质量与清晰度不会下降，并能够得到一定的增强效果。

2.2 LSD算法提取干涉条纹

2.2.1 LSD算法原理

LSD 算法是一种直线检测分割算法，它能在线性的时间内得出亚像素级精度的检测结果，并且可以自己控制误检的数量。其算法流程如图1所示。

图1 LSD算法提取直线段流程Fig.1 Flow chart of line segment extraction by LSD algorithm

1)对输入图像各像素点梯度值进行计算。尽可能少使用其他像素，以减少对彼此的依赖性。按照图2 所示选取每个像素点右下的4 个像素点计算梯度，分为x和y方向，并计算相应的梯度幅值，梯度方向的垂直方向构成水平线场（level-line）。

图2 像素点计算范围Fig.2 Calculation range of pixels

2) 对梯度幅值进行排序。在图像中具有较大梯度幅值的像素点往往意味着该像素点表征较强的边缘，而较小梯度幅值的像素点意味着梯度变换缓慢的区域，即图像中平坦的区域。由于像素值的量化问题，利用较小幅值的像素点进行运算会引入误差，采取设置阈值来拒绝此类像素点参与计算，阈值为：

式中τ为角度允许误差，一般选择为π 8。

将过检后的梯度幅值进行降序排列并分配到列表中，从具有最高梯度幅值的像素点入手，依次以列表中的像素作为种子点，进行区域生长。区域生长原则是将种子点邻域内误差小于τ且未被使用的像素点纳入生长区域，再以生长区域内满足条件的像素点为中心向外生长。整个区域的初始角度为种子点的角度，之后每添加一个新的像素到该区域，区域的角度更新为：

当区域中所有新增点的八邻域都不满足偏差条件时，停止生长。

3)对生长区域进行矩形近似。将整个区域当作一个实体，每个像素点的梯度幅值大小作为点的质量，以此计算矩形的重心。则质量为G(j)的点重心为(cx,cy)，该矩形的主惯性轴方向为矩阵M的最小特征值对应的特征向量角度。

4)对矩形近似结果进行评价。评价过程分为2个阶段：第1 阶段的依据为近似矩形内与矩形方向相同的像素点密度是否满足阈值。同向点不满足占全部像素点70%的条件，则需要以矩形的短边为标准裁剪并重新进行区域生长，直到满足阈值条件；第2 阶段为采用文献［17-18］提出的Helmholtz 原理，计算矩形中的误检数量(number of false alarms,NFA)值来确定是否接受或拒绝提取的直线，不满足NFA值则改变矩形R区域使其满足阈值为止。

2.2.2 干涉条纹提取

声压和振速在时空上具有相关性，信息上具有互补性，采用图像融合方法将二者进行融合处理，使干涉图对声场干涉结构具有更全面、清晰、多样性的描述。采用小波变换的方法，从数据级图像融合入手，将声压谱、水平振速谱的干涉图像进行融合处理，并将处理后得到的图像作为LSD算法的输入图像。

仿真环境：声速梯度选取等声速梯度，声源设置位于水下4 m 处，接收器位于水下30 m 处；相应的环境参数设置如图3所示。

图3 等声速梯度下的环境参数Fig.3 Environmental parameters under constant sound velocity gradient

在等声速梯度下，使用LSD 算法对干涉条纹进行提取，结果如图4所示，可以得到较为清晰的干涉条纹线段；采用Hough 变换及Radon 变换对干涉条纹进行提取，参数空间中峰值尖锐，提取效果较好。

图4 等声速梯度LSD算法提取结果Fig.4 Extraction results of LSD algorithm under constant sound velocity gradient

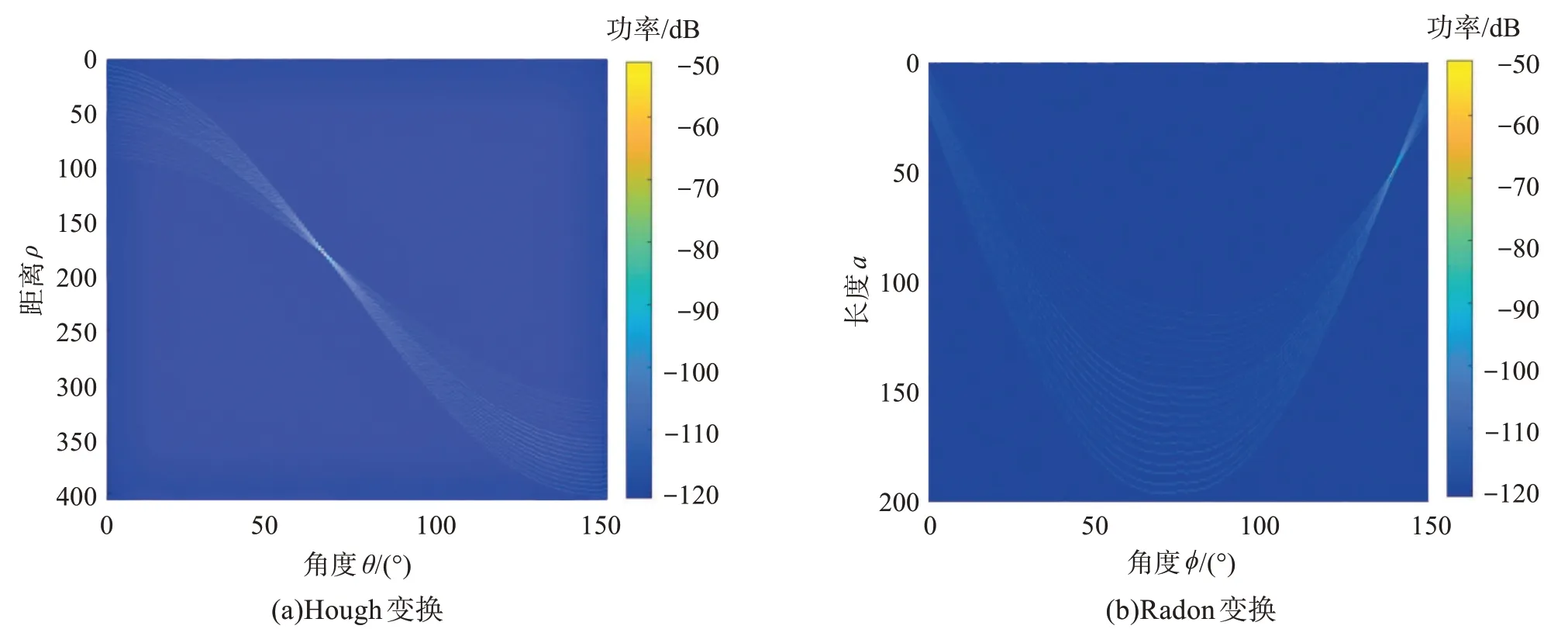
图5 等声速梯度空间变换类算法提取结果Fig.5 Extraction results of spatial transformation algorithm under constant sound velocity gradient

仿真环境：声速梯度选取SWellEx-96 试验实测的声速梯度，其表现为浅海负跃层波导环境，声源设置位于水下4 m 处，接收器位于水下100 m 处，相应的环境参数设置如图6 所示。图7 为LSD 算法提取结果，图8为空间变换类算法提取结果。

图6 SWellEx-96实验声速梯度下的环境参数Fig.6 Environmental parameters in SWellEx-96 experi‐ment under sound velocity gradient

图7 LSD算法提取结果Fig.7 Extraction results of LSD algorithm

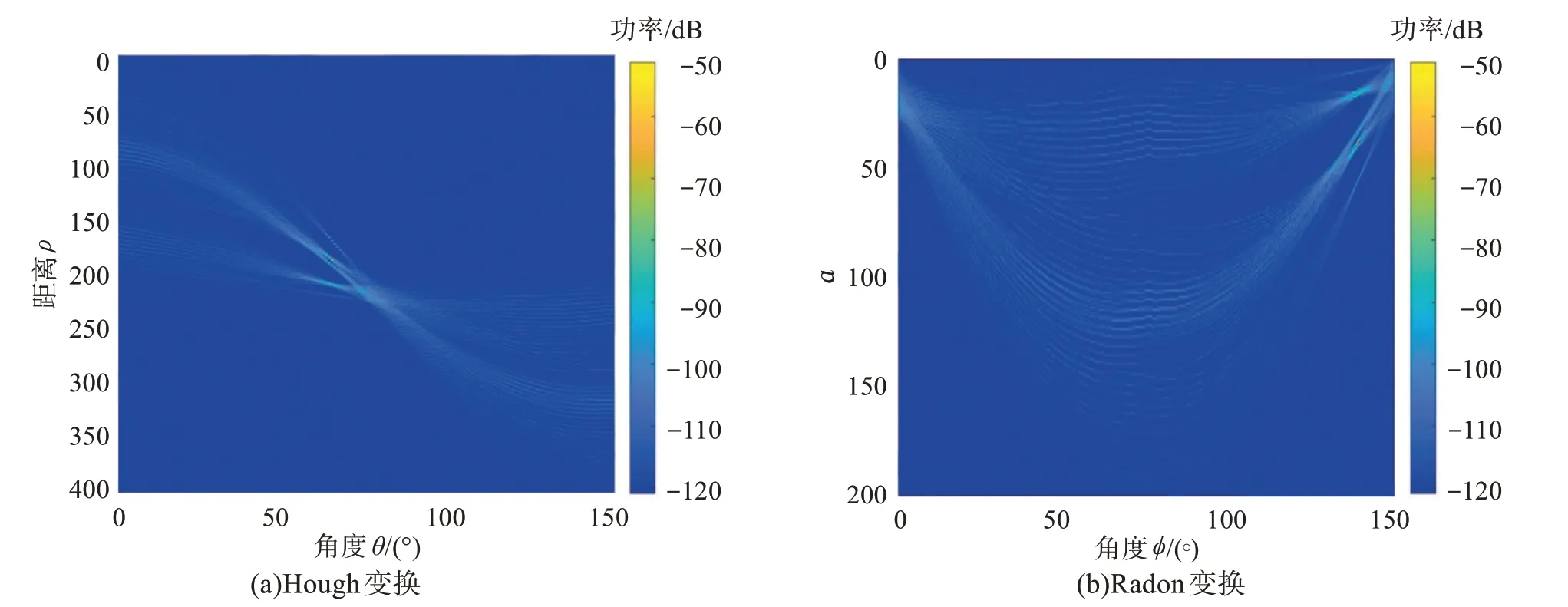
图8 空间变换类算法提取结果Fig.8 Extraction results of spatial transformation algorithm

对比图5和图8的提取结果，当波导环境较为复杂时，空间变换类算法的参数空间中出现多个亮点，峰值出现偏移，因此从参数空间中提取到合适的最值点变得较为困难。

通过比较不同声速梯度下两类算法的提取结果，可见LSD算法检测效果令人满意。并且相较于空间变换类算法有其优势所在：能够分别表征图像空间中各条直线的特征，这是空间变换类算法所没有的。

2.3 融合算法对直线提取的增强

为了更贴合实际的海洋波导环境，设置SWel‐lEx-96实验声速梯度和沉积层等海底环境共同作用下，利用LSD 算法进行干涉条纹提取时，在近程运动部分会出现许多较短的误检线段如图9 所示，为了减少这些较短线段的干扰，先采用图像融合的方式，将声压自谱与水平振速自谱进行融合，再使用LSD算法进行提取。

图9 融合前后干涉条纹提取结果Fig.9 Extraction result of interference fringes before and after fusion

对比图9 与图10，从提取结果中线段长度的统计数量可以看出，采用图像融合的方式，能够在一定程度上减少未融合前的较短检测线段数量，增加检测结果的有效性。

图10 融合前后干涉条纹统计结果Fig.10 Extraction result of interference fringes before and after fusion

3 波导不变量的估计

由式(4)、(5)可以看到，给出了2 种计算波导不变量β的方法，分别为通过建模得到简正波的相速度和群速度，利用相慢度和群慢度计算和利用图像处理方法提取距离-频率域干涉图中的干涉条纹斜率，从而计算β［16］，仿真环境设置与第2节相同。

取观测频带100～500 Hz，设置匀速运动目标速度2.5 m/s，总观测时间为8 000 s，定义目标朝向接收器运动时时间为负，远离接收器运动时时间为正。取其中-4 000～-1 000 s 的中远程运动部分，此时运动方式可以定义为靠近运动，其运动方式示意图及声场干涉结构仿真结果如图11所示。

利用相慢度和群慢度计算各相邻简正波决定的波导不变量结果如图12 所示，其数值维持在1～1.1。在相同环境下，将声压自谱与水平振速自谱进行融合，并利用LSD直线检测算法提取声场干涉结构如图13所示，并将其中所有值计算波导不变量如图14所示。

图12 波导不变量计算结果Fig.12 Computes the result of waveguide invariant

图13 融合后LSD算提取结果Fig.13 LSD algorithm extraction result after fusion

图14 线段特征统计直方图Fig.14 Statistical histogram of line segments features

按照长度排序，选取前100 的直线段计算波导不变量。从图14中可以看出，提取结果中长度小于100 的占所有线段数目中58%以上。这些较短的直线中，有很大一部分是误检结果，如果这部分直线参与到波导不变量的计算中，会拉低最终计算的波导不变量的可信程度。

选择线段提取结果中长度较长的部分进行计算如图15所示，在计算中以长度作为权重有利于降低误差，提高计算结果的可信度。

图15 线段重新排序Fig.15 Line segments are re-ordered

从图16 中可以看出，仿真的波导不变量数值大约在0.92～1.04。以直线长度为权重计算波导不变量的平均值，得到波导不变量值为0.981 4。

图16 波导不变量计算结果Fig.16 Computes the result of waveguide invariant

4 SWellEx-96试验数据处理

4.1 试验环境

试验数据选自SWellEx-96 试验期间的事件S5。在此事件中，大部分声源拖曳海域深度为180～220 m，另一半试验的声源是沿180 m等深线进行拖曳的。试验区域不存在较大的干扰，声源舰船在所有阵列的南侧开始向北航行，航行速度保持在5 kn（2.5 m/s），航行轨迹及接收阵布放情况见图17。

图17 SWellEx-96试验中S5事件情况Fig.17 Experimental situation of S5 event in SWellEx-96

舰船航行区域海深约225 m，共布放有3组声学传感器，分别为垂直阵列（VLA）、倾斜阵列（TLA）和水平阵列（HLA），处理数据选自VLA 的测量记录，21个阵元布放在深度94.124～212.5 m。

舰船牵引了2 个声源，且声源拖曳在一条等深线上，“浅源（J-13）”大约在9 m 深，发射109～385 Hz的9 个频率，编号为C-109-9S；“深源（J-15）”大约在54 m 深，发射49～400 Hz 的多条线谱。

4.2 试验数据处理

选取位于水下139.12 m 处水听器的接收数据进行处理，得到时频图，如图18所示。

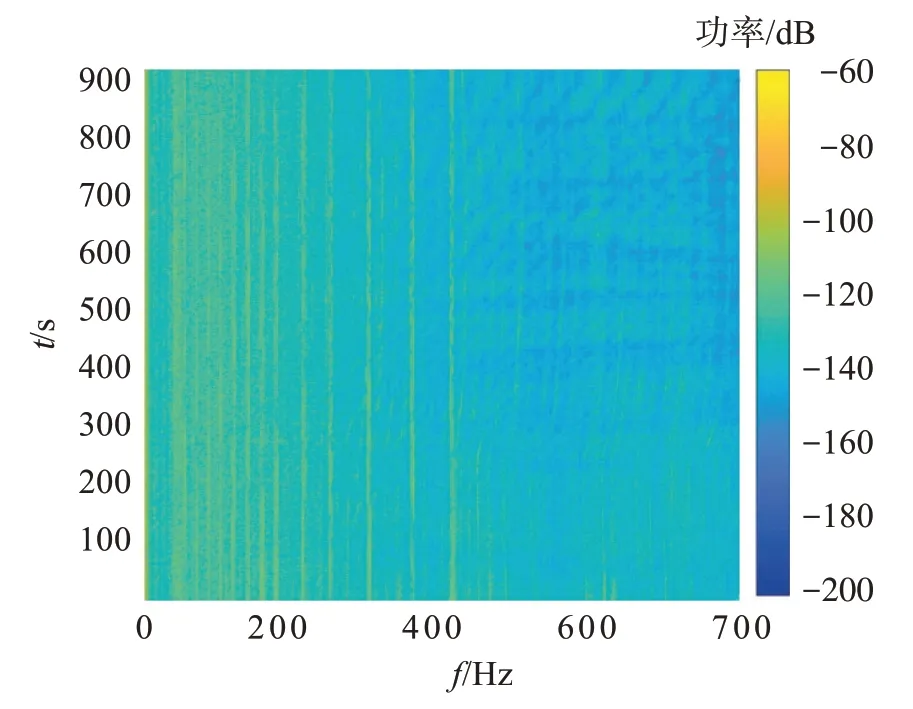
图18 接收阵元LOFARFig.18 LOFAR of receiving element

从处理结果可以看到，此次试验线谱和干涉条纹都很明显。线谱分布在49、64、94、112、130、148、166、201、235、283、338、388 Hz 附近，在400～-700 Hz可以看到清晰的干涉条纹。

选取400～700 Hz、300～900 s 范围进行LSD 算法提取干涉条纹。

4.3 试验数据处理结论

图19 为事件S5 LSD 算法提取结果。干涉条纹进行Hough 变换，如图20 所示会在变换域形成较为宽大的亮斑，无法在参数空间体现图像的细节。同样进行Radon 变换，无法在参数空间中形成可靠的亮斑，不能提取出参考线段的有效角度。使用LSD算法可以检测出较为清晰的线谱线段，剔除线谱可得干涉条纹，但是受到环境干扰等影响，加之水听器接收到的信号强度较弱，导致条纹强度不够，因此检测条纹需要进一步处理。

图19 事件S5 LSD算法提取结果Fig.19 Extraction results of LSD algorithm of S5

图20 事件S5空间变换类算法提取结果Fig.20 Extraction results of spatial transformation algorithm of S5

5 结论

1）对于大多数浅海条件，声场中存在较为稳定的干涉结构，受到声速梯度、声源和接收器深度等因素的影响，空间变换类算法随着干涉条纹偏移，提取结果也发生偏移。使用LSD 算法仍能较为详细地提取干涉条纹。

2）利用干涉条纹斜率计算波导不变量相较于简正波群慢度、相慢度的方法更为直观，在对波导不变量进行估计时可结合二者进行使用。

在本文仿真部分中对于矢量场应用的设计是利用其共有的干涉声场信息进行相同结构增强，但是在实验数据处理中发现声压信号振速信号往往不够强，导致增强效果有限且会引入新的误差，在后续的工作中，考虑研究结合弱信号提取的图像处理技术。