矢量阵自适应零陷强干扰抑制目标方位估计方法

孙纯，方尔正

（1.上海船舶电子设备研究所 水声对抗技术重点实验室，上海 201108；2.哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001）

近年来，随着各类军用装置设备（潜艇、军舰等）减振降噪技术不断进步，其辐射噪声强度不断下降，上述目标更容易被湮没在背景噪声或干扰中，导致声呐探测距离不断减小［1］。另外，由于时间和地理位置不同，舰船等所处的海洋环境在绝大多数情况下是未知且复杂的，尤其是在地理条件复杂的近海，近岸工业、航空活动及海面交通运输等都会对目标信号造成干扰，增加虚警，进而严重影响目标检测与定位。故在目前声隐身等技术不断发展、海洋环境背景干扰不断增强的形势下，如何将弱目标信号从强干扰的背景中提取检测出来十分关键，具有很大的研究意义和挑战性。

目前各类具有空域信号分离特性的技术迅速发展，其中，空域矩阵滤波技术是由Vaccaro［2］提出的对阵列信号预处理的算法，常用来进行干扰抑制，该算法通过对全空间方位划分通阻带，设置最优化问题求解滤波器，将其乘以阵列接收数据矩阵，实现通带中目标信号顺利通过，并抑制阻带中干扰信号。迄今为止，诸多学者对该技术开展了深入研究，给出了多种不同空域特性滤波器的设计求解方法。Ma‐cInnes［3］设计了最小二乘空域滤波器，并首次提出空域预滤波波束形成可获得更高探测性能；鄢社锋［4］利用二阶锥凸优化技术进行滤波器求解，并将其用于匹配场定位；韩东［5］对滤波器设计进行简化，得到各类常规滤波器的闭式解，并提出零点约束滤波器及阻带总体响应约束滤波器等的设计方法。但上述滤波器都需在先验条件下提前设计好。如阻带零点约束滤波器需已知干扰所在的较小方位范围，故无法用于干扰方位完全未知的情况；而阻带响应抑制类滤波器需已知目标方位范围，但它也是非数据依赖的，其阻带衰减幅度需预设且固定，故干扰抑制能力受限，当有强干扰时，滤波后的干扰残余量对后续算法性能有很大影响［6］。

针对感兴趣目标方位范围明确，而干扰方位范围完全未知的情况，为了克服上述常规阻带响应抑制类滤波器干扰抑制能力有限的影响，Hassanies等［7-8］等受到自适应最小方差无失真响应（minimum variance distortionless response，MVDR）算法的启发，类似地对滤波之后的信号输出功率进行约束，让其能自动形成干扰零陷，利用二阶锥规划的方式第1 次求得了数据依赖的声压阵自适应空域矩阵滤波器，进一步加强对干扰的抑制，提升了未知方位强干扰作用下声压阵的方位估计性能。

矢量水听器技术近年来蓬勃发展，矢量信号处理带来的各类性能优势吸引了众多相关领域专家对其开展研究，尝试将原本针对声压阵列的经典算法应用于矢量阵，对这些算法的研究与应用结果表明矢量阵相比声压阵更有优势，如可克服左右舷模糊，主瓣宽度更窄，旁瓣更低，尤其在阵元数不足、信噪比不高的非理想情况下矢量阵展现出了更优异的性能［9］。

基于上述研究背景，考虑结合矢量阵优势及自适应空域滤波器优势，将之前仅在声压阵信号处理中应用的自适应滤波器应用于矢量阵。本文将自适应空域矩阵滤波技术、矢量信号处理技术以及平面波方位估计技术结合，提出了适用于矢量线列阵阵元域数据，能够自适应地抑制远场强干扰的自适应空域矩阵滤波器的设计方法，并给出矢量自适应空域矩阵滤波器的最优解及推导过程。基于MVDR波束形成算法对矢量阵自适应滤波前后的远场弱目标信号进行波达方位（direction of arrival，DOA）估计的仿真，对比分析滤波器性能。并结合海试试验数据进一步验证了将矢量自适应滤波器应用在矢量阵DOA估计算法中的干扰抑制效果，试验结果表明该算法能够自适应抑制远场强干扰，显著提高了多元矢量线阵强干扰背景下弱目标信号的方位估计性能，并且相比声压阵算法效果更优。

1 矢量线阵信号处理模型

对于矢量线阵来说，被探测目标距阵列的距离D≥L2/λ时，满足远场条件，辐射的声信号经过远距离传播到达基阵后能量很小，为远场弱信号。假设有P个水下远场窄带信号，入射方向与y轴正向夹角为θ；Q个远场窄带干扰源信号（点干扰），入射方向与y轴正向夹角为φ。矢量水听器阵是由M个水声换能器构成，各个阵元位于同一水平面且间距均为d，阵的总长度为(M-1)d，建立如图1 所示的二维矢量线阵信号处理模型。

图1 矢量线阵信号处理模型Fig.1 Signal processing model of the vector linear array

接收阵列信号模型可用矩阵形式表示为：

其中：

式中：Ss(t,f)、Sn(t,f)分别为远场目标信号源矩阵和远场干扰源矩阵；As(θ,f)、An(θ,f)分别为阵列流形矩阵；N(t,f) 为加性高斯环境噪声矩阵；θ=[θ1,θ2,…,θP]、φ=[φ1,φ2,…,φQ]分别为目标信号与干扰的入射角度。

式中：c为水下声速，c=1 500 m/s。

由声压与振速的关系：

此时声矢量传感器的阵列流形为：

代入式（1）中得到矢量阵接收信号模型为：

式（6）中的阵列流形矩阵和对应的方向向量变为：

式中⊗为Kronecker 积的运算符。

2 矢量自适应空域矩阵滤波器设计

对于中心频率为f的矢量自适应空域矩阵滤波器Hv(f)3M×3M，矢量线阵滤波后的输出为：

在矢量自适应滤波器的设计上借鉴自适应波束形成算法的设计思路。MVDR 算法的原理是保证阵列在感兴趣方向上正常输出，即输出功率恒定，同时使阵列总输出功率最小，这样波束就能自动形成零陷。同理，将上述思路运用到自适应空域滤波器的设计上，通过约束通带响应和阻带衰减都在某设定范围来保证滤波器性能，同时让滤波后的阵列总输出功率最小，从而滤波器在干扰方位响应处能自适应地形成零陷［10］。具体设计过程如下：

对于矢量阵来说，滤波后信号的输出功率为：

式中：tr{·}为矩阵求迹；Rxv为矢量阵接收数据的协方差矩阵。

当采样快拍数N→∞ 时，可采用极大似然估计下的矢量阵输出数据外积的统计平均值来代替：

滤波器的设计需将全空间划分成通带区域ΘP和阻带区域ΘS，这2 个区域对应的矢量线阵阵列流形矩阵分布为Vpv和Vsv：

式中：a(θp)和a(θs)分别为通、阻带离散化后的方向向量；P和S分别为通、阻带离散化的点数。

自适应滤波器的设计准则为［11-12］：保证滤波器通带响应误差和阻带衰减分别低于设定的约束值μ1和μ2，同时满足空域滤波后的信号输出功率最小。将上述准则设计成最优化问题，表达式为：

式中：μ1为设定的滤波器通带响应误差约束值；μ2为设定的阻带响应误差约束值；Δ是设定的滤波器系数约束值。

式（12）所示的最优化问题能够使滤波器自适应地在强干扰方位放置尖锐的零陷，并保证通带响应误差和阻带约束都低于设定限制值。接下来对式（12）的最优化问题进行求解。

对矢量阵得到的接收数据协方差矩阵Rxv进行Cholesky分解，可以得到：

式（13）代入到式（11）中，可得：

式中ε为非负约束值，则式（12）可以表示为：

其中：

则可以写成二阶锥的标准形式：

之后就可以利用Sedumi 软件包对yv进行求解［14-15］，然后将其第2～((3M)2+1)个元素取出按行重排即可得到矢量阵自适应滤波器Hv。

则最终滤波输出为：

3 自适应干扰抑制算法仿真

为了验证自适应空域矩阵滤波器的干扰零陷特性以及矢量阵滤波器相比声压阵滤波器的优势，仿真对比了声压阵常规空域滤波器（CH）、声压阵自适应空域滤波器（ADH）和矢量阵自适应空域滤波器（ADHv）的空域特性。仿真选用由16个水听器组成的线阵，阵元间距为半波长0.75 m，信号为1 000 Hz的远场窄带信号，入射方位为20°，信噪比为10 dB，干扰信号的入射方位为和-40°，信干比为-50 dB。滤波器通带设置为10°～30°，其他方位均为阻带。仿真结果如图2所示。

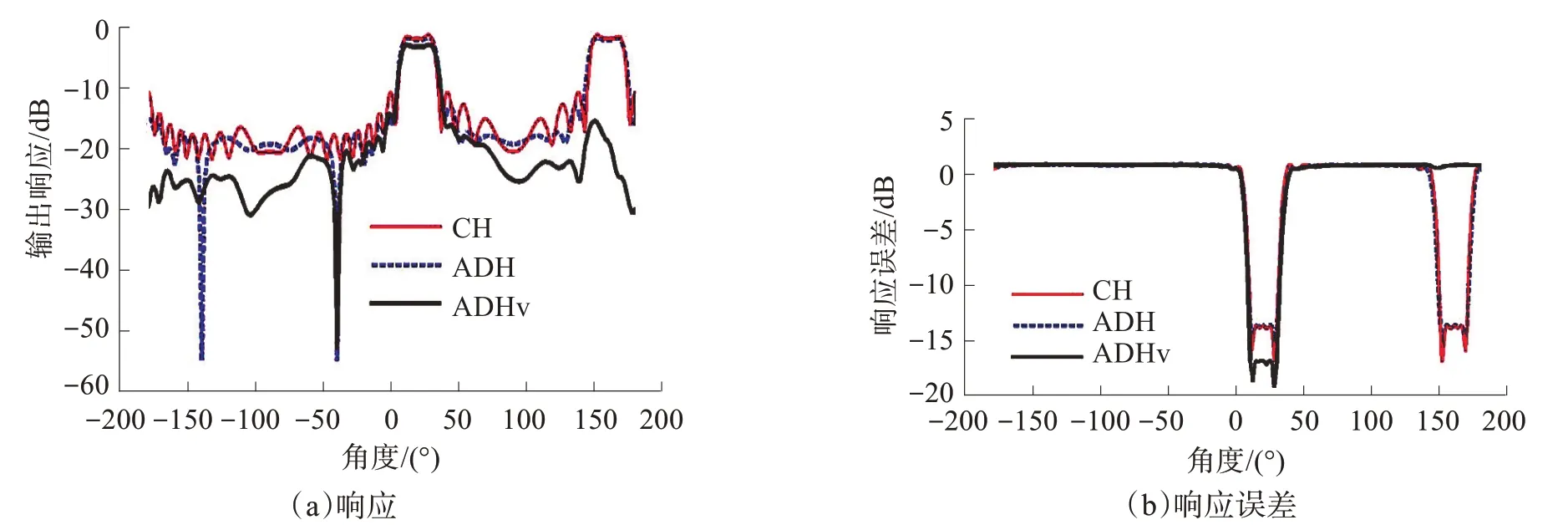
图2 滤波器空域特性对比Fig.2 Comparison of filter spatial characteristics

从图2 可以看出，自适应滤波器由于是数据依赖的，因此在-40°强干扰方位出现很深的零陷，并且总体阻带衰减低于-20 dB，而常规滤波器是非数据依赖的，不能在干扰方位形成零陷。另外，在全空间方位-180°～180°内，声压阵自适应滤波器的空域响应特性是关于90°/-90°对称的，会出现2 个对称的通带区域和2 个干扰零陷；而矢量阵自适应滤波器在全方位范围内只有一个通带区域和一个干扰方位的零陷，没有对称模糊的现象。并且矢量阵自适应滤波器相比声压阵自适应滤波器阻带响应略低、通带响应误差也略低，性能更优。

目前的声呐系统大多数情况下都采用波束形成算法进行信号检测,对于线列阵，MVDR波束形成算法较为常用。由于空域滤波后的数据仍为阵元域，故可直接用于后续MVDR 算法。矢量线阵常规MVDR波束形成器的输出功率谱表达式为：

由于滤波器通带响应与期望响应是有一定误差的，所以滤波之后的方向向量会产生一定的畸变，因此对于空域预滤波MVDR 算法需要对功率谱表达式进行一定的改善，改善后的表达式为：

式中cv(θ)=Hvav(θ)。

仿真比较常规和自适应滤波器对后续方位估计算法性能的影响，分别将它们应用在声压和矢量MVDR算法中，仿真结果如图3所示。

图3 自适应与常规预滤波DOA估计结果对比Fig.3 Comparison of DOA estimation between adaptive and conventional pre-filtering

从图3可以看出，有强干扰存在时，没有经过空域滤波的MVDR 处理结果在目标来波方位和2 个干扰方位均存在很强的峰，无法分辨哪个是真正的信号，而经过空域滤波后的结果很好的抑制了2 个干扰峰，目标方位得以凸显，且由于自适应滤波器在干扰角度有零陷产生，故得到的输出信噪比较常规滤波更高，性能更佳。另外对比矢量阵和声压阵经过自适应空域滤波之后的DOA估计结果，可以很明显地看出后者主瓣更窄，信噪比更高，将矢量自适应空域滤波器应用到矢量阵DOA 估计算法相比较声压阵自适应空域滤波处理结果及矢量阵常规空域滤波处理结果均有5 dB 左右的增益。综上验证了该算法能够较好地结合矢量阵及自适应空域滤波的优势，得到更优的方位估计性能。

4 自适应干扰抑制算法试验验证

为了检验自适应空域滤波器在矢量线列阵信号处理中应用时的方位估计性能，进一步验证第3节中的仿真结果，利用课题组自行研制的矢量水听器于2021年在吉林松花湖上进行了试验，试验过程中将五元矢量线阵通过缆绳悬挂至水下10 m，阵元间距为0.375 m（2 kHz 声波半波长）。采用双声源发射信号。信号源1 频率2 000 Hz，声源级130 dB，距离接收阵约10 m，作为感兴趣目标；信号源2频率2 000 Hz，声源级120 dB，距离接收阵约10 m，作为远场干扰。信号源布放的位置情况如图4所示。采集器设定的采样频率为65 536Hz，分段处理快拍数为1 024点。数据处理结果如图5、6所示。

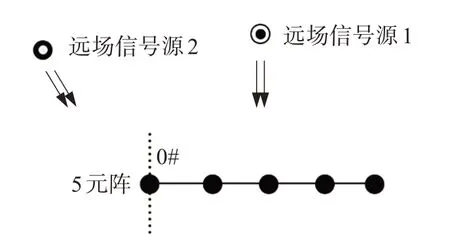
图4 信号源布放位置情况Fig.4 Position diagram of signal sources

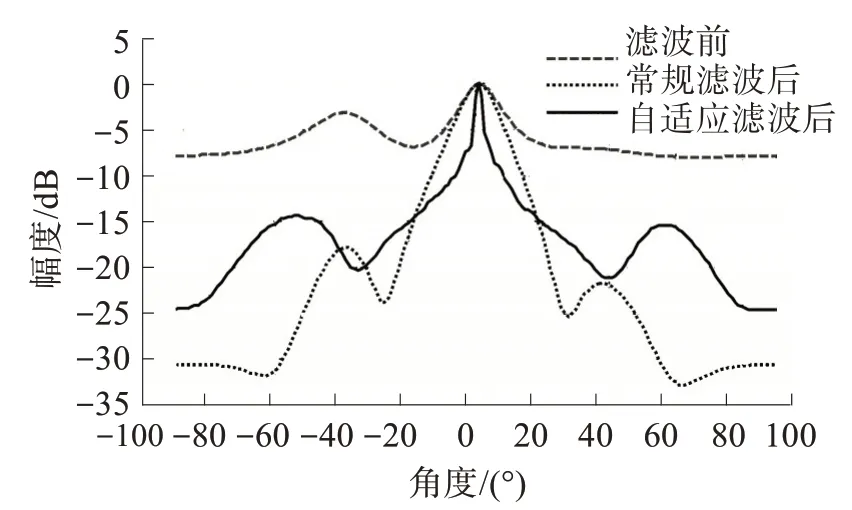
图6 矢量阵DOA估计结果对比Fig.6 Comparison of DOA estimation results

从图5、6 中可以看出，当存在具体方位范围未知的远场干扰的情况下，声压阵和矢量阵常规MV‐DR 处理结果中均存在2个较强目标，矢量阵经过常规空域滤波之后的方位估计性能大幅提升，主瓣变窄，旁瓣变低，输出信噪比增加，且滤波后的时间方位历程明确。在采用数据依赖的矢量自适应空域滤波器后，能更好地自适应抑制远场强干扰，实现对通带范围内目标的有效测向，且滤波后目标方位的主瓣宽度更窄，输出信噪比进一步提高，时间方位历程图中目标运动轨迹也更加明确，进一步验证了矢量自适应空域矩阵滤波处理应用于矢量阵DOA估计算法前的有效性及优势。

5 结论

1）本文设计的矢量自适应空域矩阵滤波器能够较好地应用于矢量线阵信号处理，通过最小化滤波后矢量阵信号总体输出功率以及约束滤波器通带响应误差、阻带衰减，产生了预期的自适应零陷干扰抑制空域特性。

2）仿真及试验结果表明，本文提出的基于矢量自适应零陷空域预滤波的目标方位估计方法，在信号方位范围明确，但干扰方位完全未知的情况下，以及高斯白噪声假设下，能够较好地自适应抑制强干扰信号，相比较声压阵相关处理及常规空域滤波处理，该算法输出信噪比以及时间方位历程图轨迹均得到了改善，验证了该算法能够有效结合矢量阵及自适应空域滤波器的优势。

3）该方法为矢量阵后置信号处理创造了更优异的条件，进而能够提高方位范围未知的强干扰背景中水下航行器矢量声呐系统的目标信号检测能力以及方位估计性能。