多智能体通信中的消息聚合策略多样化研究

庄水管， 庄哲明， 翟远钊， 戴建生

（1.天津大学机械工程学院，天津 300350；2.福建省同安第一中学，福建 厦门 361100；3.国防科技大学计算机学院，长沙 410015）

0 引言

多智能体强化学习（Multi-Agent Reinforcement Learning with Communication，Comm-MARL）在一系列具有挑战性的序列决策任务中取得了广泛的应用［1-2］，如交通控制［3］和多用户策略游戏［4］等。在Comm-MARL中，如何高效地通信仍是一个有待进一步解决的问题，也是多智能体协调的关键技术［5］。智能体可通过通信的方式来交换其本地的观察结果，这些通信的消息由分散的智能体聚合和处理后，可用于增强学习策略和选择行动的单个本地观察，实现智能体共同优化的目标［6］。

如何聚合消息是决定通信效率的关键因素［7］。为模拟智能体之间的相互作用关系，Comm-MARL 普遍使用图形神经网络（Graph Neural Networks，GNN），该方法基于图实现了对多智能体环境的表征。多智能体系统通常被建模为一个完整的图，每个智能体对应其中的一个节点［8］。作为最受欢迎的GNN变体之一，图注意力网络（Graph Attention Networks，GAT）在Comm-MARL的开发中具有巨大的潜力［9-10］。GAT 由节点和边组成，经过注意力加权的消息通过边在节点之间进行消息传递。近年来，GAT在多智能体强化学习中被广泛使用，其中智能体可以被表示为节点，智能体之间的通信可通过GAT中的消息传递来实现。

消息聚合可通过通信图的注意力加权消息传递来实现。尽管GAT在Comm-MARL中被广泛应用，但研究人员发现其获得的消息聚合策略通常缺乏多样性［11-12］。从本质而言，图中大多数节点可能会过度关注某一个节点，并经常受到其的过度影响［13］。究其原因，对于大部分的多智能体场景，同一消息的重要性对于不同状态的智能体而言是不同的。智能体之间采用同构的消息聚合策略将导致大部分的智能体过度关注一部分无意义的消息，导致通信效率低下［14-15］。

为使智能体能够探索不同的消息聚合策略。研究多智能体通信图的邻接矩阵，并提出消息聚合的同质性可通过矩阵的秩和核范数来衡量。基于此提出一种基于核范数的正则化器，用于对邻接矩阵做正则化约束，以主动丰富Comm-MARL 中消息聚合策略的多样性。通过这种方式，不同的智能体可以探索不同的行为，以增大获得最优协调策略的可能性。

1 方法设计

提出了一种即插即用的正则化器，名为“核范数正则化”（Nuclear Norm Regularization，NNR），图1 中说明了如何使用该正则化器。对GAT 中每一层的邻接矩阵做正则化约束。

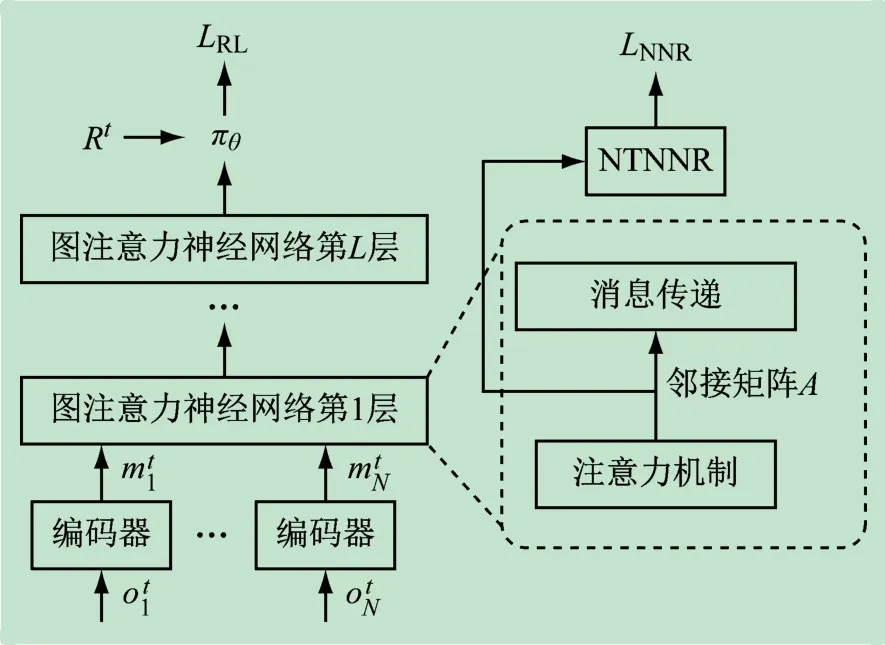
图1 将NNR集成到基于GAT的多智能体通信方法

1.1 用矩阵的秩衡量消息聚合的多样性

对于每个智能体i，GAT 计算中所有邻接节点表示的可被训练的加权平均值

式中：W'和W包含可学习的参数；“‖”为向量的拼接。

邻接矩阵A 的元素是智能体之间互相的注意力得分，使用Softmax 函数在所有邻接节点之间进行归一化

式中：i、j为智能体编号；Ni为智能体i的邻居智能体。邻接矩阵A满足以下属性：

将从邻接矩阵A的第i行和第j行中选择的向量为ai和aj。如果智能体i和j具有同质的消息聚合策略，则ai和aj的区别会比较小。在这种情况下，ai和aj可被视为近似的线性相关。相反，不同的消息聚合策略意味着线性独立的向量。因此，可用邻接矩阵A 的矩阵秩来衡量消息聚合的多样性或同质性。

1.2 核范数正则化

众所周知，矩阵的秩优化问题是多项式复杂程度的非确定性问题（Non-deterministic Polynomial Hard），因此提出一种利用核范数的替代方法。邻接矩阵A的奇异值可表示为σi（i＝1，2，…，N），则邻接矩阵A的核范数

核范数也称为迹范数或Schatten-1 范数。可通过约束最大化邻接矩阵的核范数来增加消息聚合策略的多样性（以下在包含两个智能体的系统中进行分析）。

对于任意二阶矩阵

邻接矩阵A的核范数

将λ记为ATA的特征值，E为单位矩阵，则有：

令‖λE-A‖＝0，则有：

解得：

则有邻接矩阵A的核范数

结合式（3）中给出的邻接矩阵的属性，可得核范数‖A‖*最大的邻接矩阵

可见，NNR可起到增大邻接矩阵中消息聚合时的权重差异，获得更多样性的消息聚合策略，丰富多智能体通信的多样性，促使智能体之间达到更好的任务分工状态。该结论可推广到矩阵阶数更高的情况。

1.3 整体优化目标

在图注意力通信算法中采用NNR 可使消息聚合的策略具有多样性。遵循大多数Comm-MARL 方法，使用共享参数分散化范式（Policy Decentralization with Shared Parameters，PDSP ）的近端策略优化算法（Proximal Policy Optimization，PPO）作为框架。则Comm-MARL原始损失函数的梯度

为发现不同的消息聚合策略，将NNR应用于GAT层的邻接矩阵A。第l层GAT 中NNR 的相应损失函数

式中，θl为用于生成第l个GAT层的邻接矩阵A的图神经网络参数。

通过最小化以下损失函数来更新模型参数θ，即

式中，λl是l层的NNR 的正则化权重。为在训练过程中使λl逐渐衰减，引入新的缩放超参数βl，则

2 实验结果

通过交通路口和星际争霸II 多智能体挑战两个实验，评估NNR 在两种广泛使用的场景中的性能，分别验证NNR对消息多样性和实验成功率的提升作用。

在交通路口的场景中，分析多样化消息聚合的必要性。而星际争霸II 多智能体挑战环境是近年来评估各种强化学习研究成果的常用基准。其中，选择了两种最先进的通信Comm-MARL 方法，分别是博弈抽象通信法（Game Abstraction Communication，GAComm）［16］和深度隐式协调图-集中执行-长短期记忆法（Deep Implicit Coordination Graphs-Centralized Execution-LongShort-TermMemory， DICG-CELSTM）［17］。将NNR与它们集成后进行实验。所有的实验结果均通过3 次运行后取平均值而得出。

2.1 交通路口场景

交通路口场景：边长为18 个网格的正方形实验场，实验场上有双向交叉路线、4 个终点和若干具有1个网格视野的汽车（即智能体）。汽车需要通过通信来避免发生碰撞。将环境中最大的汽车数量设置为20 辆，并设置最大的动作执行次数为50 次，新的汽车被添加到环境中的概率为0.05。实验成功的定义是一定时间内没有汽车之间的碰撞发生。每辆汽车在每个时间步内的可选择的动作是前进或刹车，奖励包括-0.01 的步进成本和-10 的碰撞惩罚。

策略网络包含2 个GAT 层，分别设置GAT 层的NNR的缩放系数β1＝0.01、β2＝0.005。对于目标不同终点的智能体，NNR可鼓励它们获得不同的消息聚合策略。智能体的消息聚合策略在不同时间点都在不断地变化。为分析NNR对消息聚合策略的影响，在图2 时刻中用训练好的策略对2 个智能体的消息聚合策略进行可视化评估。图中的数字为智能体的编号。

图2 交通路口场景中的实验测试帧

如图2 所示，智能体5 号位于左上角，智能体9 号位于右下角。即使它们之间可以通信，这些信息对彼此都是无意义的。图3 为具有代表性的智能体用于消息聚合的注意力分数值的分布。通过使用NNR，智能体5 号和9 号获得了不同的消息聚合策略。实验结果表明可使得多智能体系统中的消息通信更加高效，也减少了不相关的智能体之间的不必要的通信干扰。

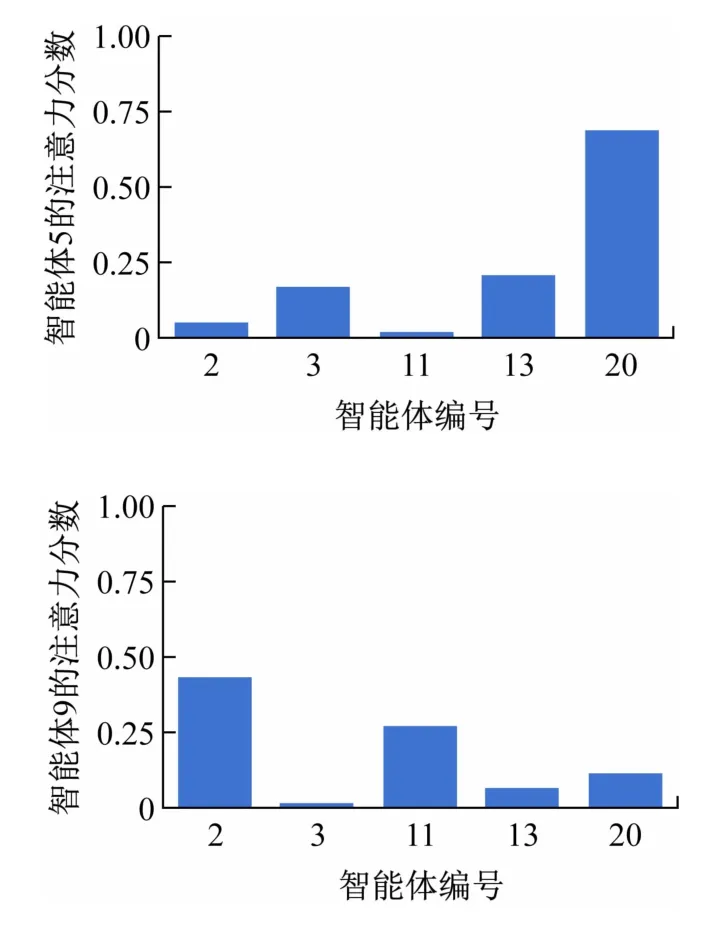
图3 智能体5和9的消息聚合策略

2.2 星际争霸场景

基于前述实验的结论，可在更复杂的星际争霸场景中进行测试，以证明NNR的通用性和有效性。星际争霸II多智能体挑战环境是实时战略游戏《星际争霸II》开发而来，该环境需要使用算法对多个智能体进行微操作。其中，每个智能体都由独立的控制器控制，且必须根据本地观测的数据采取下一步的动作。

NNR通过即插即用的方式，便于和现有的基于图的多智能体通信方法集成。选择多智能体通信强化学习算法中最先进的算法之一DICG-CE-LSTM［17］，并将NNR应用于其中。所有超参数与原方法一致，缩放超参数β1设为0.005。选取星际争霸II 多智能体挑战环境中的实验地图，其初始化状态如图4 所示。

图4 实验地图的初始化状态

在该实验的地图中，双方选手各拥有3 名跟踪者和5 名狂热者。相比于跟踪者，狂热者可以造成更高的伤害，但其速度更慢。该实验的算法将控制左侧选手的跟踪者和狂热者，与右侧选手的队伍进行对战，首先消灭对方所有场上角色的一方获得胜利。

该实验记录的采用NNR 作为正则化器与原算法的平均获胜率如图5 所示。与不采用NNR 的方法相比，加入NNR 正则化项的方法展现了出色的性能，明显拥有更高的胜率。因为多样化的消息聚合策略带来的多样化行为策略，使得群体智能得以涌现。

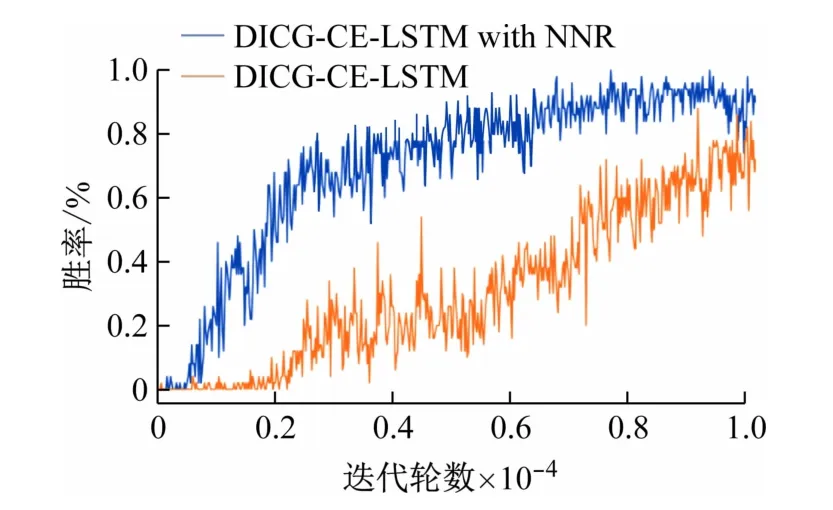
图5 采用NNR作为正则化器时与原算法的性能比较

更进一步可将最终的训练策略可视化如图6 所示。在实验地图中，3 个狂热者具有相同的策略网络参数，且具有相似的局部观测，但可做出不同的行动，最终包围对方的跟踪者进行攻击，获得胜利。复杂的协调策略直接反映了NNR 带来的消息聚合多样化的效果，体现了算法的有效性。

图6 算法训练的最终策略可视化

3 结语

本文提出用矩阵的秩来度量多智能体通信中消息聚合的多样性，使用核范数来量化多样性。即插即用正则化器NNR，可主动丰富消息聚合的多样性。实验结果表明，相比现有的消息聚合方法，加入NNR 正则化项的GAT可达到更高的渐进性能和更好的训练效率。NNR可以很容易地集成到现有的基于图建模的多智能体通信方法，而且可有效提高算法的性能，具有较高的应用价值。