弯扭组合变形实验的改进与探讨

朱飞鹏， 杜宁宇， 雷 冬

（河海大学a.力学与材料学院；b.河海里尔学院，南京 211100）

0 引言

电阻应变测量（电测）技术［1-5］是力学领域十分重要也很实用的一项技术。利用电阻应变效应将待测力学量转化为电学量进行测试，掌握该项技术可以为学生从事与工程监测方面的工作打下坚实的实践基础。当前，我国大多数工科院校开设的基础力学电测实验基本包括梁的纯弯曲正应力实验和薄壁圆管的弯扭组合变形实验［6-12］。梁的纯弯曲正应力实验比较简单，主要利用单臂半桥（1／4 桥）测量纯弯曲段的正应力；弯扭组合变形实验综合性较强，需要学生选择合适的桥路来实现一点主应力、弯曲正应力和扭转切应力的测试。

在弯扭组合变形实验中，粘贴好的应变花由3 个位于不同方向的单个应变片构成。然而，实际上3 个应变片并没有粘贴于构件表面同一点处，从而引入了测量误差，这也正是主应力测量精度不如正应力高、弯曲切应力精度远低于扭转切应力［13-14］的原因。因此，对原有弯扭组合变形实验装置进行改进，粘贴多个由3 个单片叠于一处的应变花，并对主应力、扭转切应力、弯曲切应力测试精度进行分析与讨论。

1 改进的弯扭组合变形实验装置及理论分析

弯扭组合变形实验装置及薄壁圆管的横截面如图1 所示，圆管一端为固定端，另一端固接长a＝200 mm的钢制拐臂。圆管在集中力F作用下产生弯扭组合变形，待测截面I-I到自由端距离l＝300 mm。实验采用逐级等量加载方式，荷载增量ΔF＝100 N。实验参数如表1 所示。

表1 弯扭组合变形实验装置参数

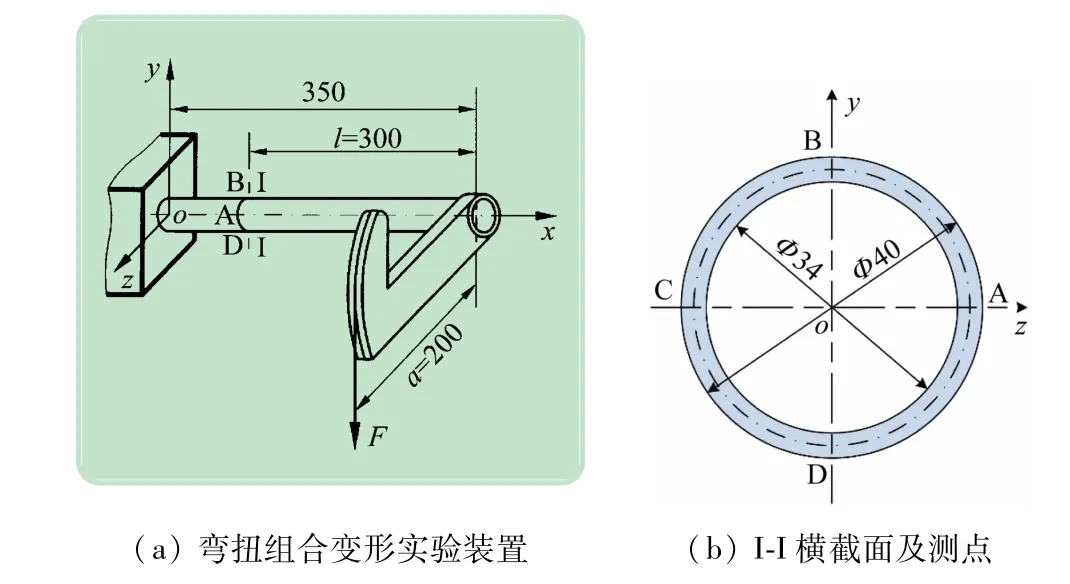
图1 薄壁圆管弯扭组合变形实验装置示意图（单位：mm）

如图2（a）所示，在截面I-I表面前、上、后、下4 个测点A、B、C、D处各布置一枚三轴45°应变花（型号为中航电测BE120-3CB），应变花3 个单片的中心重叠于一点，并与轴向分别成-45°、0°、45°；4 个测点12 个应变片的编号为R1～R12。共点应变花能够测量构件同一点不同方向的线应变，因此更适用于应力分析。图2（b）为弯扭组合变形实验最常见的应变花粘贴方式，应变花3 个单片分别对应构件上不同的测点，一般适用于较大构件（或应力变化不显著）的测点应力分析，对于弯扭组合变形实验中的小构件而言，精度受到影响。

图2 2种应变花贴片方案

当荷载增量ΔF＝100 N 时，I-I 截面弯矩M＝30 N·m，剪力FS＝100 N，扭矩T＝20 N·m，计算得到该截面的最大正应力σmax（B点拉、D点压）、弯曲切应力τS（A点和C点）、扭转切应力τT（表面各点都一样）、B点（二向应力状态）主应力σ1、σ3和方向角α0的理论值，结果如表2 所示。

表2 圆管I-I截面的3 种应力及B点主应力理论值

2 主应力测试

为测试B点主应力，将-45°、0°、45°方向的应变片R4～R6按照1／4 桥路连接到应变仪，得到的应变值（ΔF＝100 N）分别为ε4＝ε-45°＝111 ×10-6，ε5＝ε0°＝141 ×10-6，ε6＝ε45°＝-16 ×10-6。根据下式计算主应变及其方向：

再由广义胡克定律计算得到主应力实验值，即：

式中：εⅠ、εⅡ为测点的2 个主应变；α0为第一主应变εⅠ的方向角；ε4、ε5、ε6分别为测点B处应变片R4～R6的应变测量值。主应力实验值如表3 所示。结合如表2 所示的主应力理论值，得到第一、第三主应力和方向角的测量误差。此外，还利用如图2（b）所示的传统实验装置进行了主应力测量，得到的测量误差如表3 所示。通过对比发现，采用改进装置后，无论主应力还是方向角的精度都得到了有效提高（误差绝对值都小于5%）。原因主要是，改进装置的应变花3 个单片测量了同一点的线应变。

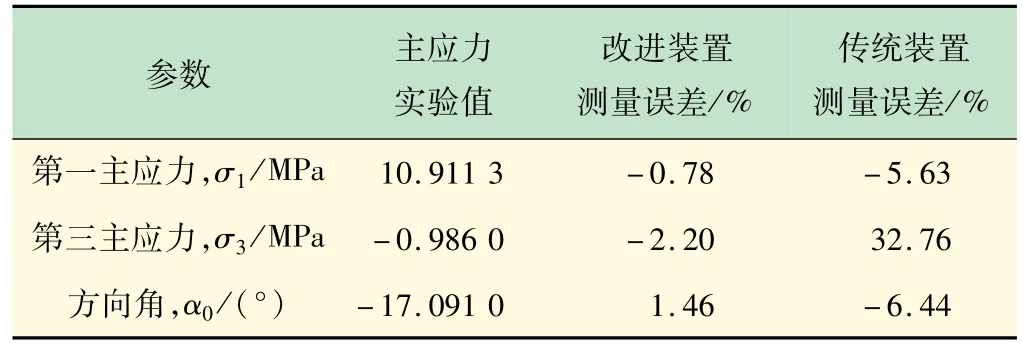
表3 B点主应力测量结果

3 泊松比测试

通常弯扭组合变形实验会给出圆管材料泊松比的值，便于后续应力分析。其实，即使不给出泊松比的值，也可以利用测点应变花的应变测量值进行估算，而估算值是否准确则与测点不同方向应变的测量精度有关。前文已经验证了改进装置具有优异的应变测量精度，因此利用B点应变花测量值来估算材料泊松比。

对于如图1（a）所示的圆管正上方B点（应力状态见图3（a）），沿圆管轴向（即沿图1 中x轴或0°方向）和横向（即沿图1 中z轴或90°方向）的应变计算式为：

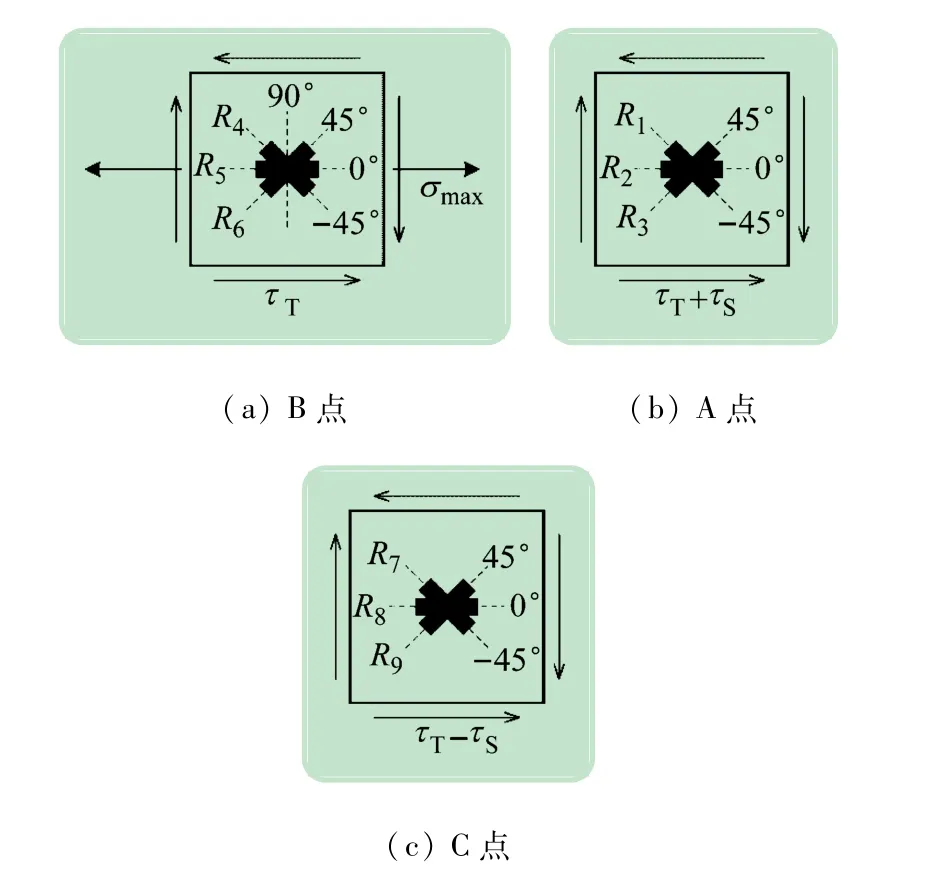
图3 B、A、C点应力状态

只要已知式（3）中的2 个应变值，就可计算出泊松比的值。然而，该点应变花3 个单片都没有沿着横向粘贴。由平面应力状态和广义胡克定律分析［15］（或直接利用平面应变状态分析）得出与圆管轴线成±45°方向的线应变分别为

由式（3）和式（4）易得

将B点-45°、0°、45°方向的3 个应变值代入下式计算泊松比

利用前文中的测试值ε-45°＝111 ×10-6，ε0°＝141 ×10-6，ε45°＝-16 ×10-6，代入式（6），得到泊松比ν ＝0.326 2，该数值与表1 中给出的0.33 仅有1.15%的误差。此外，利用如图2（b）所示的传统装置对泊松比进行了测量，结果为0.361 7，误差为9.61%。弯曲正应力和弹性模量亦可测试，由于比较简单，这里不再赘述。

4 扭转切应力与弯曲切应力测试

在弯扭组合变形实验中，一般只要求测试扭转切应力，这主要是由于弯曲切应力测量精度较差，高达50%以上［13］，实验效果不佳。当应变花±45° 2 个应变片偏离了测点时，将引入附加弯曲正应力，从而严重影响弯曲切应力测量结果。改进装置则不存在该问题，可以较准确地测量出扭转切应力与弯曲切应力。

实验装置上A 点、C 点应力状态如图3（b）、（c）所示，选择±45°方向的应变片，即R1、R3、R7、R94 个应变片，应变组成如下：

式中：εT45°、εS45°分别表示由扭转切应力τT和弯曲切应力τS所引起的45°方向的线应变绝对值；εt为应变片热输出。利用电桥的加减性，得出以下2 个全桥形式：

式中，εd1、εd2表示采用全桥连接得到的应变仪读数。可以发现，±45° 2 个应变片粘贴于同一测点，不存在附加弯曲正应力的影响。根据广义胡克定律得到的扭转切应力τT和弯曲切应力τS计算式为：

对R1、R3、R7、R94 个应变片先后按式（8）中2 个全桥进行测试，得到应变仪读数εd1＝39 ×10-6，εd2＝250 ×10-6，再代入式（9），得到切应力实验值，并与表2 中理论值进行比较，结果如表4 所示。此外，表4 也给出了基于图2（b）传统装置的测量误差。对比可知，改进装置在保证扭转切应力精度的同时，还将弯曲切应力测量误差从47.73%减小至10.50%。

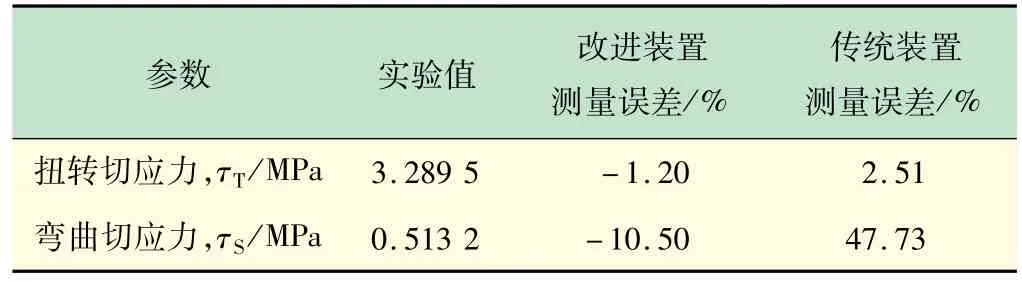
表4 扭转切应力与弯曲切应力测试结果（A、C点）

值得关注的是，弯曲切应力误差10.50%仍然偏大，原因是应变仪的输出读数较小（εd1＝39 ×10-6），1 ×10-6的读数浮动即引起2.5%的差异。一般地，构件的弯曲切应力较小（比正应力小至少一个数量级），所引起的线应变也较小，相应的应变仪读数应变也小，使得测量精度较差（这也是为何组桥时要尽量选择半桥和全桥的原因，可以增大应变仪读数）。因此，可不采用粘贴±45°应变片测量弯曲切应力，而通过测量出的弯矩反算剪力，再计算得到弯曲切应力，这样精度较高。对于薄壁构件，扭转切应力与弯曲正应力相当（3倍关系），因此扭转切应力测量精度可以满足要求。

5 结语

当前大多数高校采用的弯扭组合变形实验装置普遍存在主应力测量精度不高、弯曲切应力测试误差大的问题，主要原因是组成应变花的3 个单片没有严格位于同一测点，而是存在位置偏差，这对于小尺寸薄壁圆管构件而言，带来的误差不容忽视。为了提高实验测试精度，采用3 个单片叠于一处的应变花对弯扭组合变形实验装置进行改进，并将测试结果与理论值进行对比，得到以下结论：①对处于二向应力状态的B点主应力进行了测定，主应力和方向角的测量误差均在3%以下；②提出了一种测试泊松比的方法，与给定值之间的误差为1.15%；③利用A、C测点测试了扭转切应力和弯曲切应力，其中扭转切应力的测量精度基本不变，弯曲切应力测量误差为10.50%（改进前为47.73%）。

·名人名言·

科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种“偶然的机遇”只能给那些有素养的人，给那些善于独立思考的人，给那些具有锲而不舍的精神的人，而不会给懒汉。

——华罗庚