信号失真度测量装置设计

李 岳， 程春雨， 吴振宇

（大连理工大学a.控制科学与工程学院；b.创新创业学院，辽宁 大连 116024）

0 引言

在信号传递的过程中，人们总是希望信号能够完整地传递到目标接收端，但在传播的过程中，信号或多或少会有所损失。随着时代的发展，保证信号的长距离传播俨然已成为对利用信号的基本要求，为了保证信号传播后的质量，信号失真度的精度控制正是现代电信号传播的需求之一。失真有谐波失真、互调失真、相位失真等多种，而总谐波失真（Total Harmonic Distortion，THD）则能够在一定程度上说明信号在传播过程中损失了多少，从而接收端的用户能够采取合理的措施来判断该信号是否能够被利用［1］。谐波失真是由放大器的非线性引起的，失真的结果是使放大器输出产生了原信号中没有的谐波分量，使信号受到噪声干扰，如果输出的是音频信号，严重时会失去原有音色。

近些年来，国内电子技术的快速发展促进了信号处理方法的进步。传统的THD 处理方法有基波抑制法、谐波分析法、模拟法。基波抑制法是一种间接测量法，其无法直接测量出失真定义值；谐波分析法操作计算复杂，在低频段一般不采用此种方法测量失真度；模拟法的失真度测量受于前级电路有源器件的非线性，因此对小信号的测量不够准确。传统方法的局限性需要更有效的方法来改进THD的处理方法，数字化方法则能很好地完成目标，能够得到高精度的THD 测量结果。

本文用数字化方法设计并制作了谐波失真度测量装置，重点研究了低频段的THD数字化测量装置及测试，以达到设计的测量时间、精度等要求。

1 总体设计方案

本装置使用RIGOL DG2052 信号发生器来完成被测信号的模拟输入。信号发生器产生的信号经低通滤波器滤除噪声，电压跟随器隔离前后级电路，自动增益控制电路放大信号，再用电压偏置电路给信号加上直流电压偏置，输入模数转换器进行模数转换。模数转换后，得到微控制器接口允许范围内的离散的电压序列，再输入到微控制器单元（Microcontroller Unit，MCU），进行快速傅里叶变换（Fast Fourier Transform，FFT）运算，并输出THD的计算结果，最终运算结果可在显示设备上观测［2-3］。装置的总体设计原理如图1所示。

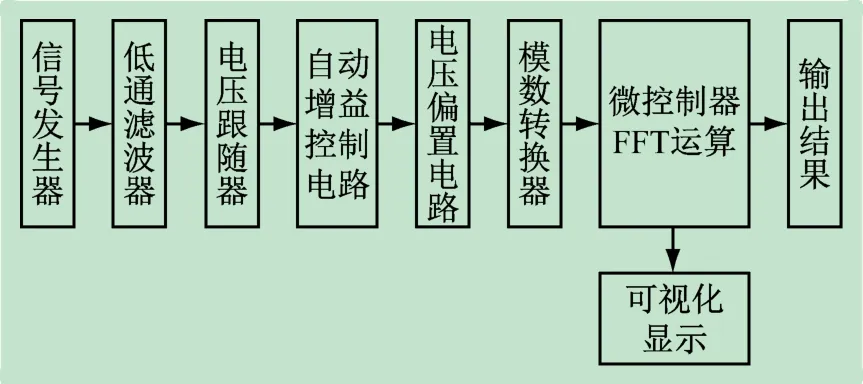
图1 装置总体设计原理图

本文的FFT是利用计算离散傅里叶变换（Discrete Fourier Transformation，DFT）的快速算法［4］，其计算式为

式中：X［n］为离散的采样序列，n＝1，2，…，N；X［k］为其频域的转换结果，k＝1，2，…，N；N为DFT变换区间长度。

在程序设计中，采用ARM Cortex-M4 内核的CMSIS-DSP库的库函数进行1 024 点FFT 运算，则可得到离散采集信号的FFT运算结果［5-6］。将FFT转换后的结果计算为电压值，THD的计算式为

式中，Uox为各次谐波的电压峰峰值。

2 装置的电路设计

2.1 MCU主控制器

MCU 选择了TI 公司的MSP432E401YT 微控制器，控制器内核为ARM Cortex-M4。主频最高可以达到120 MHz。内置高精度数模转换（Analog to Digital，AD）电路，单个通道最高采样频率可达到1 MHz。可以完成中低频段的信号采样要求。

2.2 四阶低通滤波电路

四阶低通滤波电路选用高精度运算放大器TL082来设计，TL082 内部集成了运算放大器，其高转换速率，低偏置输入，低噪声等特点也很好地契合了系统的设计需求［7］。通过2 个二阶滤波器级联来得到四阶滤波器［8］。四阶滤波器倍频程为24 dB。

2.2.1 二阶低通滤波电路分析

采用SALLEN-KEY 型滤波器［9］的二阶低通有源滤波器的电路如图2 所示。阻容网络C1、R1和C2、R2组成二阶低通滤波器，Rf和R3确定电路放大倍数。根据电阻分压，可调增益的SALLEN-KEY 型低通滤波器的通带电压增益

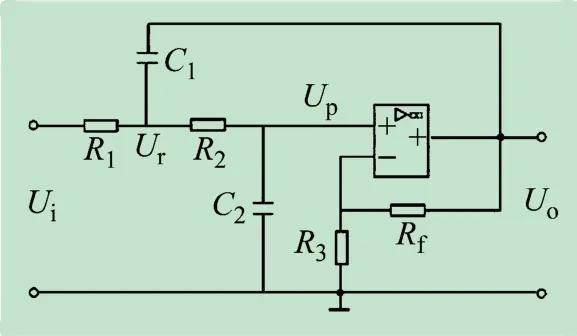
图2 二阶低通有源滤波器电路图

式中：Ui为输入电压；Ur为图中节点电压；Up为运放同相输入电压；Uo为输出电压。先将R3断开，Rf短路，则可由KCL得到如下关系式：

式中：ω为数字频率；t为时间。由拉普拉斯变换可得：

式中，s为复频率。由此，UP、UO与Ur的关系为

联立式（2）和（3）可得传递函数

式中，C2＝m×C1，m为电容比例系数。而二阶振荡系统的标准传递函数［10］为

式中：ω为谐振频率；ξ为阻尼系数。联立式（2）～（5）可得谐振频率和阻尼比，即：

通过截止频率即可算出电容值大小。

由式（6）可计算R1、R2、R3、Rf的电阻值，即：

2.2.2 四阶滤波器电路设计

利用滤波器设计软件Filter ProDT 进行滤波器电路设计，主要设计参数：滤波器阶数为4；电路级联级数为2；阻带频率为2 kHz；通带频率为1.834 kHz；阻带衰减为-3 dB。另外，VCC与GND之间加上滤波电容可消除噪声干扰。经2 个二阶低通滤波器级联后的四阶低通滤波器电路如图3 所示。

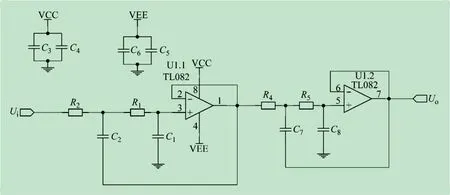
图3 四阶低通滤波器电路图

2.3 AGC自动增益控制电路

AGC自动增益控制电路采用可变增益，可变增益放大器（Variable-Gain Amplifier，VGA）芯片为AD603，可实现以dB 为单位的线性增益控制［11-12］，其工作电路如图4 所示。图中在AD603 芯片的VOUT与FDBK之间接入合适的REXT 值可以获得不同的增益范围值；在FDBK与COMM之间接入电容作频率补偿［13］。当REXT ＝2.15 kΩ 时，增益范围为：-1 ～+41 dB。GNEG和COMM 接地，VOUT 和反馈端FDBK 通过电阻R7相连接，选择最大带宽模式。OPA197 的输出信号UG接到GPOS形成反馈控制。通过调节电位器R14即可改变输出电压UG的大小，从而完成输出电压的自动增益控制，其增益

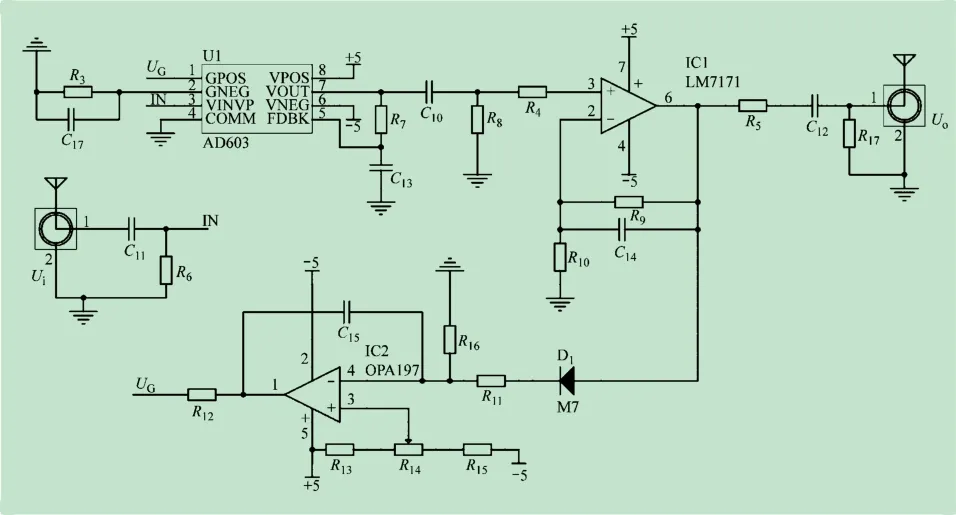
图4 AGC自动增益控制电路图

2.4 电压偏置电路

电压偏置电路给输入的交流信号提供了直流偏置电压，使其满足ADC的采样条件。本文采用无源电路设计，如图5 所示。通过改变Rp的电阻值分压，从而调节直流偏置电压的大小。

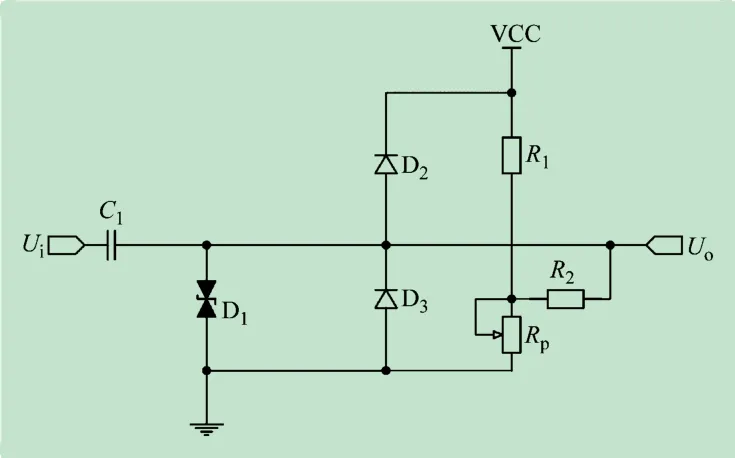
图5 ADC采样偏置电路图

使用瞬态抑制二极管（Transient Voltage Suppressors，TVS）对电路进行保护，一旦瞬时电压超过电路正常工作电压后，TVS二极管便发生雪崩效应，提供给瞬时电流一个超低电阻通路，从而使得后级I／O口避免受到损毁［14］。D2与D3二极管的作用为防止电源反接，提供了一个放电回路，从而保护工作电路在电源反接的情况下不被损坏。

3 程序设计

设计的MCU程序流程如图6 所示，先对MCU 的时钟和通用输入／输出端口（General Purpose Input／

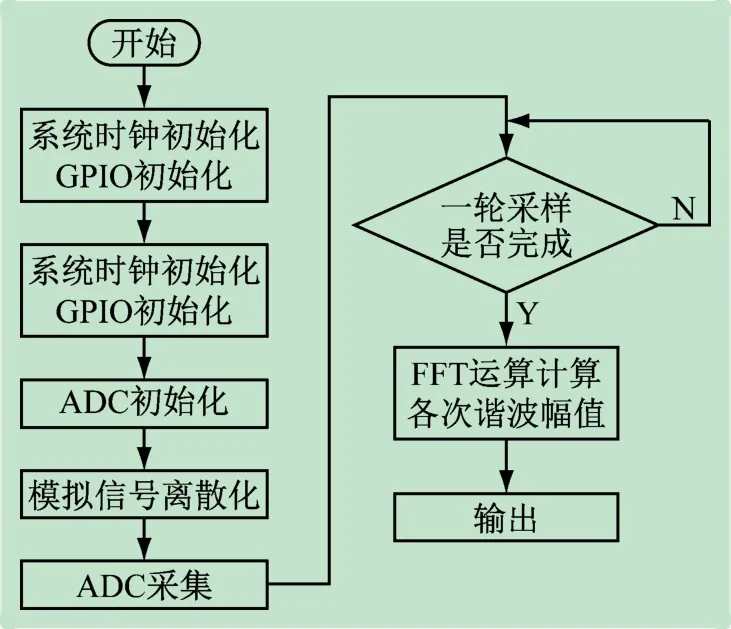
图6 MCU程序流程

Output，GPIO）进行初始化，使系统正常运行，再对ADC进行初始化。初始化完成后，将离散信号输入至MCU，通过MSP432E401YT对离散的序列进行FFT 运算，从而得到各次谐波的电压峰峰值。

4 实验部分

4.1 实验仪器与装置

本实验配套需用信号发生器和直流稳压电源：待测信号由RIGOL DG972 信号发生器产生；系统供电电源采用RIGOL DP832 数字电源。实验装置的实物连接如图7 所示。

图7 实验装置测试实物连接图

4.2 实验步骤

连接好线路的实验装置上电后，装置即自动初始化。待初始化完成后，调节信号发生器为谐波信号发生模式，配置输入信号为五次谐波，基波频率为1 kHz，待测信号的峰峰值分别为30、300、600 mV。具体实验操作步骤如下：

步骤1将输入端连接至RIGOL DG2052 信号发生器；将电路各部分供电端连接至电源；外部电路的输出端连接至MSP432E401YT的ADC采集I／O口。

步骤2检查线路连接无误后，开启电源。

步骤3调节信号发生器输出5 次谐波，基波信号频率设置为1 kHz。

步骤4预置THD分别为0.05、0.25、0.5。

步骤5调节待测信号的电压峰峰值分别为30、300、600 mV，记录液晶显示屏（Liquid Crystal Display，LCD）上的THD显示结果。

步骤6调节待测信号的电压峰峰值分别为30、300、600 mV，基波信号频率分别为1、2、3、4 和5 kHz，随机选取待测信号的失真度进行测量，观察装置显示的测量结果并记录。

5 实验结果与分析

实验信号输入至装置后，经过前级电路对信号进行调理，再输入至MCU 的ADC，最后通过软件处理，计算出THD。测量显示的结果为THD、电压峰峰值经归一化的幅值和THD的最大相对误差，测量所造成的绝对误差与被测量真值之比所得的相对误差［15］

式中：Δ 为绝对误差，L为THD 理论计算值，δ 为相对误差。输入信号频率1 kHz 下THD 实验结果如表1所示。表1 中，基波频率为1 kHz，待测信号电压峰峰值分别为30、300、600 mV，THD计算值为预置值。

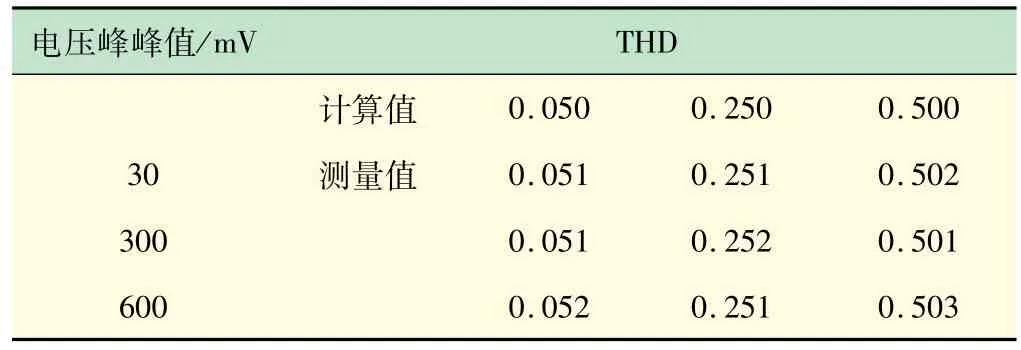
表1 输入信号频率1 kHz下THD实测值

实验中，待测信号的电压峰峰值分别为30、300、600 mV，基波信号频率分别为1、2、3、4 和5 kHz，失真度随机选取，装置在5 s 内完成了单次测量。归一化幅值为各次谐波电压与基波电压之比的理论计算值，THD计算值为所选取信号的理论计算值，THD测量值为实验测得的显示结果，测试结果如表2 所示。

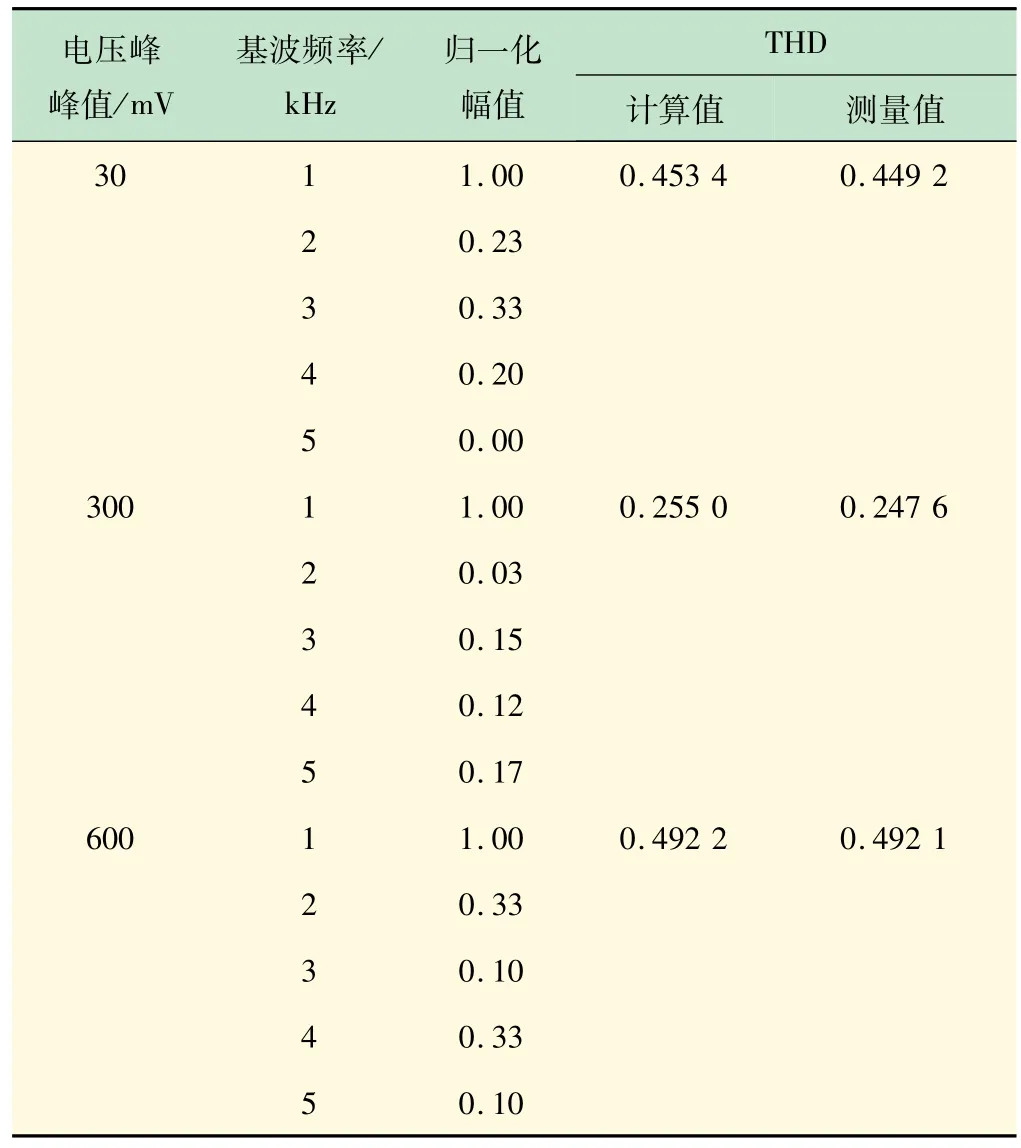
表2 基波频率为1 kHz信号失真度测量比较

在THD预置取值条件下，通过测量数据计算得，最大相对误差为

在THD随机取值条件下，通过测量数据计算得，最大相对误差为

与理论计算值比较表明，测量误差在装置设计的范围内；对比表1、2 可知，装置的THD 实际测量值与理论计算值基本一致。结果表明：装置测量误差小于5%；单次测量完成时间小于5 s。

6 结论

本文以FFT算法、AGC自动增益控制电路为核心设计了THD谐波失真度测量装置，在使用了FFT算法提高了运算效率。通过失真度测量实验，验证了其可行性。结果表明：数字化方法在处理低频段信号方面相较于传统的信号处理方法具有优越性；所设计的装置在处理低频段信号时，具有良好的性能和较高的精度。目前实验装置的信号测量频率范围有限，还需进一步优化。

·名人名言·

只有严格的专业化能使学者在某一时刻，大概也是他一生中唯一的时刻，相信自己取得了一项真正能够传至久远的成就。今天，任何真正明确而有价值的成就，肯定也是一项专业成就。

——马克斯·韦伯