分数阶控制伺服电动机实验演示平台设计

程国扬， 贺名扬

（福州大学电气工程与自动化学院，福州 350108）

0 引言

当前大学工科教育改革的一个核心导向是深化科教融合和产教融合［1-3］。在设置专业课程的教学内容时，要及时纳入学科领域的前沿技术，引导学生把前沿技术付诸实践、解决实际问题，加快先进技术向现实生产力的转化过程，这对促进经济发展、实现科教兴国具有重要的意义［4-6］。

在控制工程领域，最近一个重大进展就是分数阶建模和控制技术［7-9］。这种技术可用于提高伺服系统的跟踪性能［10-11］。分数阶微积分可看成是对整数阶微积分的推广。由于其概念抽象（不像整数阶微积分具有清晰的物理涵义，如：位置、速度、加速度）和计算的复杂性，分数阶微积分的发展一直较为缓慢，且局限在纯数学的领域。一些学者发现采用分数阶导数对一些复杂的过程进行建模，能更准确和细致地描述系统的动态特性，特别是一些具有记忆特性的过程对象；Oustaloup等［12］提出分数阶鲁棒控制的概念与技术，并应用于汽车悬架控制；Podlubny［13］提出分数阶比例-微分-积分（Proportional-integral-derivative，PID）控制器的模型，作为对目前工业控制中广泛应用的PID 控制技术的一个推广。分数阶控制已成为控制领域的一个热门研究方向。由于其算法实现的复杂性，在工程应用方面相对滞后。

为向自动化专业本科生和控制类的研究生介绍分数阶控制技术，设计了一个基于永磁交流伺服电动机的分数阶控制系统实验平台，分别实现了目前主流的几种控制算法，即分数阶PID、分数阶自抗扰控制（Active Disturbance Rejection Control，ADRC）和分数阶滑模控制（Sliding Mode Control，SMC）。通过数字信号处理器（Digital Signal Processor，DSP）的算法编程，对电动机进行速度调节或点位伺服控制。通过实验平台的运行，学习分数阶控制技术的具体应用。鉴于伺服电动机是构成工业自动化系统的核心器件，伺服控制的快速性与准确性对生产效率和产品精度（质量）有直接的影响，在既定的硬件系统之上，引入先进的控制技术，使伺服性能得到显著的提升，充分体现了人的主观能动性和先进理论方法的价值，能给人带来一种成就感。这种实践对提高学生的学习积极性和专业认同感大有益处。

本文将对分数阶控制技术的伺服电动机实验示范平台的具体设计加以介绍，并通过实验测试结果，展示其应用方法和控制效果。

1 分数阶控制器的设计

1.1 分数阶微积分

分数阶微积分算子t0Dαt是对整数阶微积分的扩展［9］

式中：f（t）为自变量t的函数；t0与t分别为自变量的下界（初始值，t0＝0 时可省略不写）和当前值；实数α是微分／积分的阶次。在复频域，分数阶算子可表示为sα。

分数阶微积分的定义（计算法则）有多种形式，在控制领域应用较多的分别是Grunwald-Letnikov（G-L）定义、Riemann-Liouville（R-L）定义和Caputo 定义，这3 种定义在适当的条件下是等价的。本文采用G-L定义：

式中：h为计算的步长；［·］为取最接近的整数；是二项式系数

式中，Γ（·）是Gamma 函数，定义为：Γ（γ）＝。如果计算步长足够小，式（2）的计算可近似为

式中，wk＝，可按以下方式递推计算：

在实时控制中，式（4）的计算只能采用有限项求和（截断），随着时间的推移，可能带来严重的误差。为避免这个问题，可采用Oustaloup提出的整数阶滤波器，在选定的频域区间［ωb，ωh］内用一个N阶线性滤波器来近似拟合分数阶微积分算子t0Dαt的频率响应特性［9］：

1.2 分数阶PID控制

分数阶PID 控制器在控制领域中受到广泛关注［13］。其传递函数

由于此控制律PIλDμ比常规PID多了2 个可调参数，即微分阶次μ和积分阶次λ（0 ＜λ，μ ＜2），因而增强了控制器设计的灵活性，可获得更好的控制性能和鲁棒性。对一阶系统（如电动机速度伺服系统），通常采用分数阶PI控制已足够。考虑如下的一阶系统：

式中，a≥0 和b＞0 是模型参数。采用如下的分数阶PI控制律：

其对应的频域响应

控制系统的开环传递函数为G（s）＝C（s）P（s），对应的频域响应为G（jω）＝C（jω）P（jω）。控制律设计要满足以下准则：相角裕度为φm；在截止频率ωc附近相频曲线平坦（即其导数为0），以保证控制系统的增益鲁棒性。于是得到［8］：

由式（11）可解得：

由式（12）可得：

联立式（14）、（15）可确定ki和λ 的值，但因为它们是非线性耦合方程，难以得到解析解，可借助Matlab采用图解法来得到其数值解。

最后，由式（13）可解得：

1.3 分数阶自抗扰控制

自抗扰控制（ADRC）在各种实际控制系统中得到成功应用［14］。自抗扰控制的核心思想是把系统模型不确定性和外部扰动归结为一个等效总扰动，利用扩展状态观测器（Extended State Observer，ESO）对系统状态和总扰动进行实时估计，并采用状态误差非线性反馈与扰动补偿来构成控制律。应用ADRC 的难点是参数较多、参数值选择较复杂。

考虑典型位置伺服系统，其传递函数

为设计ADRC控制律使系统输出量y准确跟踪给定目标r，针对上述模型设计一个非线性ESO

式中：z1、z2和z3为观测器的内部状态量；ε ＝z1-y；δ为正参数，通常可取δ ＝5Ts，其中Ts为离散采样周期；β01、β02和β03为观测器增益（正标量）。可根据选定的观测器带宽ωo来整定［15］：

非线性函数fal（·）定义如下：

式中，sign（·）是标准的符号函数。常规的自抗扰控制律如下：

式中：β1、β2、α1，α2为正参数；e1＝r-z1，e2＝˙r-z2。

式（18）、（20）是ADRC 控制器的核心部分，必要时还可引入一个微分跟踪器（或滤波器）来安排瞬态过程。控制律（20）包含了对状态跟踪误差的非线性PD反馈，其参数对控制性能影响很大，但参数值与性能指标之间的关系并不明朗，导致参数整定很困难。文献［16］中提出把式（20）中的PD反馈律改为分数阶PD控制律，利用分数阶控制的灵活性来提高控制性能，但文献中未给出参数整定方法。借鉴上一节的思想，推导出分数阶参数的计算公式。

考虑如下的分数阶PD控制律

其对应的频域响应为

由系统（17）和控制律（21）构成的开环系统频域响应为G（jω）＝C（jω）P（jω）。类似于上一节的设计思路：选择相角裕度φm，并保证相频曲线在截止频率ωc附近平坦（导数为0），可得到与式（11）～（13）类似的联立方程，从中可解得：

由于难以直接从式（23）和（24）得出kd和μ的解析解，此处仍需采用图解法来确定其数值。相应地，可确定参数kp如下：

最后，分数阶ADRC控制律

1.4 分数阶滑模控制

滑模控制是一种常用的鲁棒控制技术，本节在非奇异终端滑模控制的框架中引入分数阶微积分，以进一步提高控制系统的性能。

针对系统模型（17），考虑系统的模型不确定性和扰动，可把模型改写如下：

式中：y、v分别为伺服系统的位置输出量（可量测）和速度；u为控制量（转矩电流）；d为由负载扰动、摩擦力矩和其他不确定因素折合而成的总扰动。

考虑目标信号r，定义跟踪误差为e＝y-r，则有：以及

定义滑模变量

式中：β ＞0，α∈（1，2）；fs（˙e，α）＝sign（˙e）·｜˙e｜α。求σ对时间的一阶导数，得：

为使σ→0，选取如下的滑模控制律：

式中：β1＞0，β2＞0，这里包含一个分数阶积分算子D-γ，参数γ∈［0，1］。

在控制律（30）中用到速度和扰动信号，需利用观测器来估计其值。这里将直接借用1.3 节的扩展状态观测器（18），最终的控制律

2 伺服电动机实验系统及控制流程

式中：θr为电动机的机械转角，rad；ωr为机械角速度，rad／s；J为电动机的转动惯量，kg·m2；kf为黏性摩擦系数，Nm·s／rad；TL为负载转矩，Nm；kt为电磁转矩系数，Nm／A；iq为q轴电流（转矩电流），A。

实验中采用42JSF630AS-1000 交流伺服电动机，其额定电压和电流为24 V 和4.2A，额定功率为64 W，额定转矩和转速为0.2 Nm和3 000 r／min，极对数是4，配置了1 000CPR 的增量式光电编码器。采用TMS320F28335 作为主控芯片以及基于智能功率模块FSBB30CH060 的驱动电路，构成电动机控制系统，如图1 所示。

图1 伺服电动机控制实验系统

系统采用双环控制结构。其中内环对转矩电流iq和励磁电流id进行闭环调节，外环则对转角θr或转速ωr进行控制，控制信号是内环电流iq的给定值。当角位置θr作为系统的受控输出量时，电动机的运动模型可转化为式（27）的形式，其中，a＝和b＝为系统参数。若仅考虑速度调节，则可得到式（8）所示的一阶模型。为数值处理方便，这里的角位置以圈（Revolution，简写为rev）为单位，速度单位为r／s。通过系统辨识，确定模型参数值：a＝3，b＝700。

采用Code Composer Studio 软件对电动机的控制算法进行编程，设置一个频率为10 kHz的ePWM中断程序来执行电流内环控制（采用抗饱和PI 控制律）；外环（位置或转速）采用本文介绍的控制律，其控制周期为Ts＝2 ms，即每20 个内环周期执行一次外环控制，并限定外环控制信号（转矩电流命令）的饱和限幅值为4 A。在主程序中，循环刷新数据显示，并根据按键来处理电动机的启、停和给定变化。控制系统的程序流程如图2 所示。

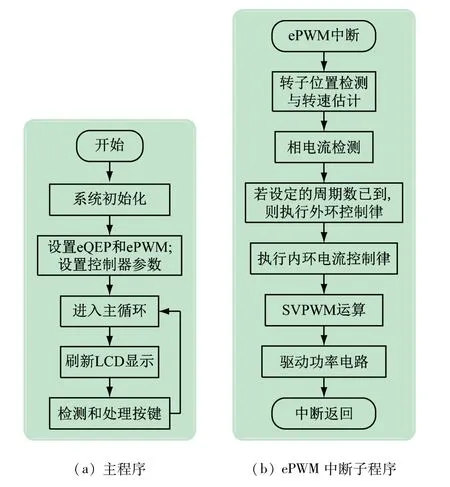
图2 交流伺服电动机控制流程

3 实验测试

在永磁交流伺服电动机试验台上进行实验测试。采用分数阶PI 控制进行速度调节。选择相角裕度φm＝65°和截止频率ωc＝100 rad／s，得到分数阶PI控制律的参数见表1。

表1 控制律参数值

其中分数阶算子采用Oustaloup滤波器来逼近，对应的参数：ωb＝0.000 1 rad／s；ωh＝1 000 rad／s；N＝10。滤波器采用双线性变换来离散化（其他控制律中的分数阶算子也采用相同的滤波器参数）。图3 给出了目标转速为10 r／s的实验结果，其速度响应较快、超调约为10%、无稳态误差。

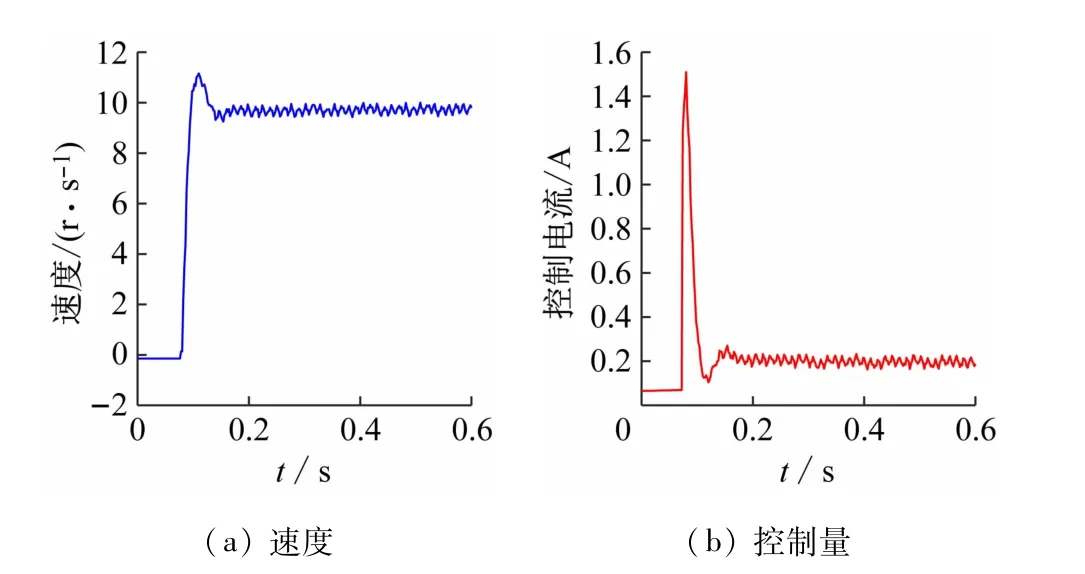
图3 分数阶PI控制的实验结果（速度给定＝10 r／s）

利用分数阶ADRC 进行位置控制。选择相角裕度φm＝65°和截止频率ωc＝100 rad／s，可得到分数阶ADRC控制律的相应参数，选取观测器带宽参数ωo＝100 rad／s，整个控制律的参数见表1。分别进行了目标位置为1 圈（r＝1 rev）和2 圈（r＝2 rev）的位置控制实验，其结果在图4、5 中显示，分别给出了位置、速度（估计值）、控制量（转矩电流给定）和等效扰动（折合到输入通道的扰动值，即z3／b）的波形，其中位置和速度信号由于其数值范围不同，分别在同一子图的左右两侧纵轴标示其刻度。可见，位置控制的稳态性能较好，瞬态过程有一些超调，控制律的参数有待进一步优化。

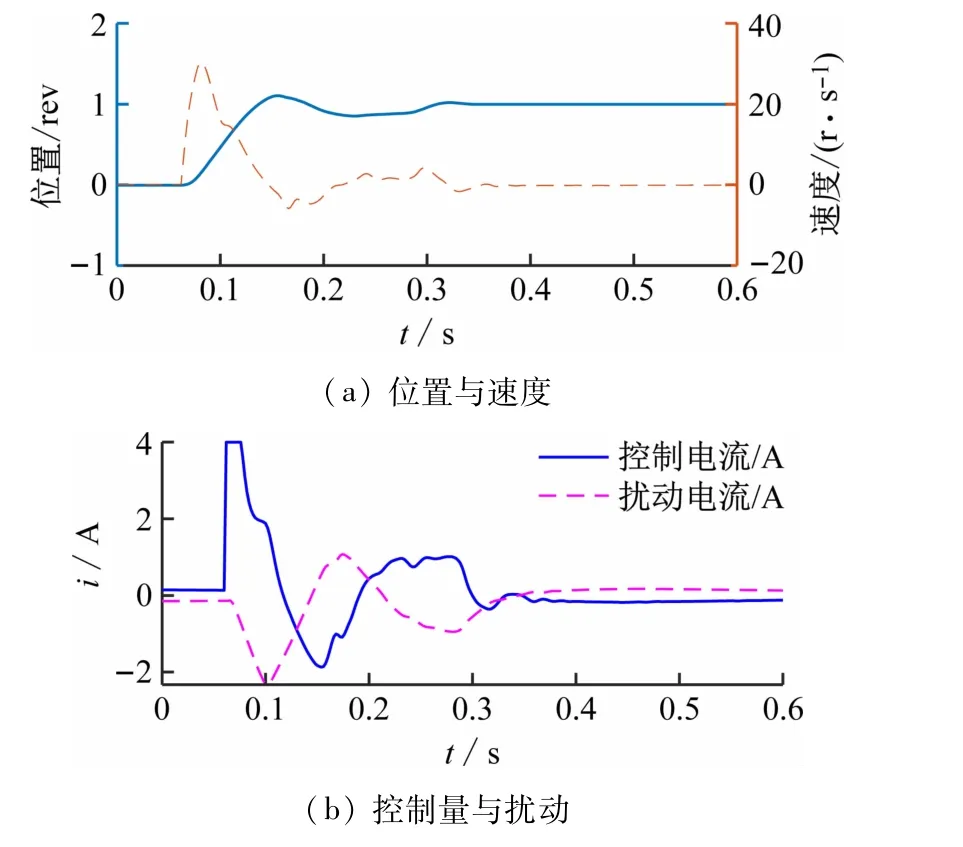
图4 分数阶ADRC控制的实验结果（位置给定＝1 rev）

图5 分数阶ADRC控制的实验结果（位置给定＝2 rev）

测试分数阶滑模控制器，选取的参数值见表1，它与分数阶ADRC 共用一个状态观测器。分别设置目标为1 圈（r＝1 rev）和2 圈（r＝2 rev），相应的位置控制实验结果在图6、7 中显示。显然，在这2 种情况下，位置响应曲线都具有快速平稳的瞬态性能，而且稳态误差可忽略。但分数阶滑模控制的参数较多，参数调优需要一定的耐心和技巧。

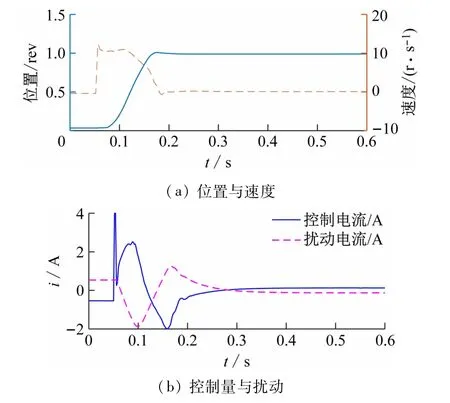
图6 分数阶滑模控制的实验结果（位置给定＝1 rev）

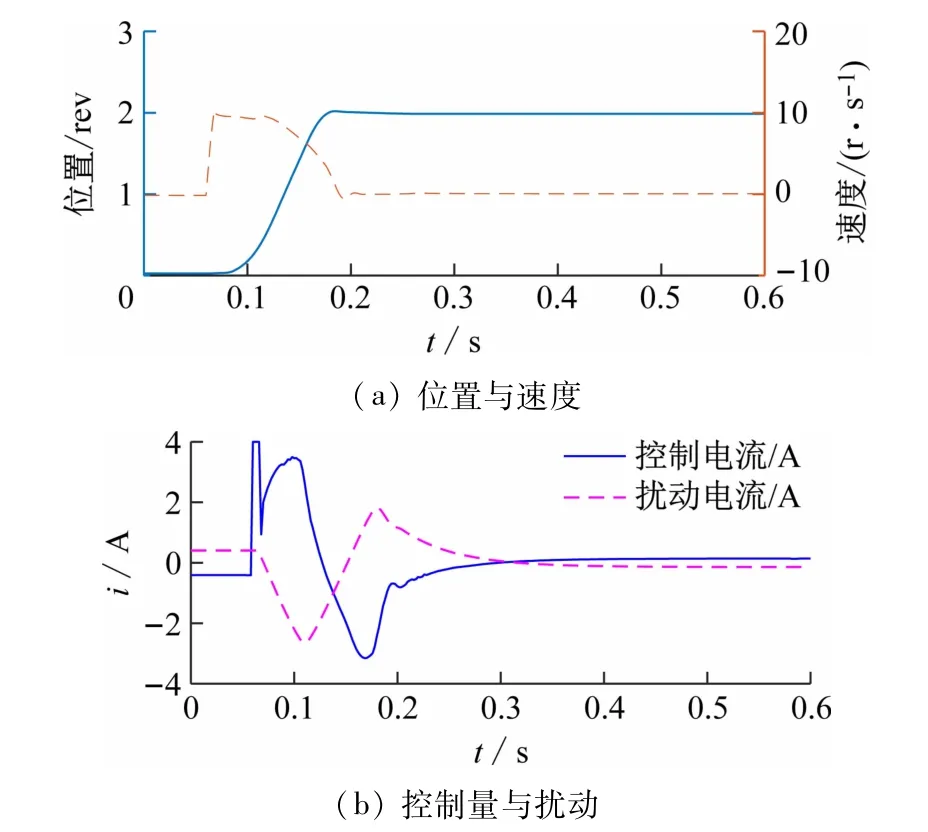
图7 分数阶滑模控制的实验结果（位置给定＝2 rev）

4 结语

本文介绍了一个适用于自动化本科、控制学科研究生的交流伺服电动机分数阶控制实验示范平台，给出了分数阶PID控制、分数阶自抗扰控制和分数阶滑模控制律的具体设计。通过基于TMS320F 28 335的实时控制实验，展示了控制方案的有效性。分数阶控制作为一项新技术，要用于实际系统，需经过技术理解、问题建模、方案设计、软硬件实现和调试优化这几个主要步骤，设计这个实验示范平台就是为了加快应用流程，帮助学生快速掌握分数阶控制的相关技术和伺服控制系统的实时编程和实验调试方法，培养学生的工程实践技能。下一步，将探索分数阶控制系统的参数自校正、自整定技术，使这个实验平台更完善、更具实用性。