多特征的灰度反转和旋转不变直方图

何骥鸣， 廖福林， 林远长， 高 明， 曾维信

（1.重庆城市管理职业学院智能工程学院，重庆 401331；2.中国科学院重庆绿色智能技术研究院电子信息技术研究所，重庆 400714）

0 引言

纹理特征包含了物体表面的结构组织信息，反映了图像中的同质现象，在基于内容的图像检索中得到了广泛的应用，对模式识别和计算机视觉等领域有着重要意义。在图像处理领域提出了多种纹理描述符用于纹理分割、纹理分类和场景识别，其目标是用纹理区分图像或物体。但这一目标会受到许多因素的影响，且当图像受到旋转、尺度、光照等干扰时，分类任务的难度会显著加大。

经典的局部二值模式（Local Binary Pattern，LBP）［1］是较早提出的基于灰度差分编码的纹理描述符，为了捕捉更微妙的图像纹理特征提高图像分类性能，研究者们基于LBP 提出了更多改进的纹理描述符。其中，完整局部二值模式（Completed LBP，CLBP）［2］通过CLBP-C、CLBP-S、CLBP-M 等3 种描述符，将中心像素与近邻像素间差分的幅值和符号分开考虑，获得了更细微的纹理特征。完整的局部二值计数（Completed Local Binary Count，CLBC）［3］通过统计LBP模式中1 的个数提取特征，局部三值模式（Local Ternary Pattern，LTP）［4］使用软阈值将像素局部差分编码为三值，局部编码变换特征直方图（Locally Encoded Transform Feature Histogram，LETRIST）［5］显式地对图像特征空间和尺度空间中的局部结构信息进行联合编码，局部空频模式联合编码（Joint Coding of Local Space-Frequency Pattern，JCLSFP）［6］利用局部量化的空频模式刻画纹理，并保留了特征表达的判别性。

当图像灰度发生反转时会干扰生成的二值码，导致二值码部分或全部反转，降低图像分类精度。为此，有研究者提出了一些方法抵消这种变化所导致的分类精度下降，如梯度局部二值模式（Gradient Local Binary Pattern，GLBP）［7］、局部梯度模式（Local gradient Pattern，LGP）［8］利用梯度与差分编码来克服灰度反转，利用LBP等价模式克服图像旋转，因此特征本身对图像旋转变化不具有鲁棒性。非冗余局部二值模式（Nonredundant Local Binary Pattern，NRLBP）［9］使用补码提取特征，使其具有灰度反转不变性，但没有考虑旋转不变性。排序的局部梯度模式（Sorted Local Gradient Pattern，SLGP）［10］利用主导强度顺序度量和LBP标准模式克服灰度反转与旋转，特征本身仍然不具有旋转不变性。局部分组不变序模式（Local grouped invariant order pattern，LGIOP）采用强度和距离顺序进行编码，使特征同时具有反转及旋转不变性。

为了捕捉更微妙的图像纹理特征，进一步提高图像分类精度，同时克服图像发生灰度反转时分类性能下降的问题，设计了一种改进的不变性灰度反转和旋转不变直方图（Grayscale-Inversion and Rotation Invariant Histogram，GIRIH）：①捕捉更微妙的图像纹理特征；②构建对线性灰度反转变化具有鲁棒性的多种互补特征；③采用联合编码克服灰度反转变化。以期使提出的GIRIH能够在提高图像分类性能的同时，克服灰度反转导致分类精度下降的问题。

1 GIRIH特征分析与方法

GIRIH的主要原理是先对图像滤波获得图像微分最大值和最小值；再基于微分信息构建对线性灰度反转变化具有鲁棒性的多种互补特征；最后对不同的特征进行联合编码，进一步克服反转时灰度值的正负变化，从而具有旋转不变性。与以往的纹理描述符相比，所提的GIRIH特征在编码过程中加入了多种互补特征，具有灰度反转和旋转不变性，在联合编码中，每一个特征都采用了合适的量化阈值。

1.1 高斯导数滤波

由于图像自身含有丰富的结构信息，而各种滤波器能可控地提取图像局部或全局的结构信息，因此可以利用一阶、二阶高斯导数滤波器得到图像的一阶、二阶微分结构信息［5］。

假设给定图像I，利用高斯一阶、二阶导数对图像进行滤波，得到沿x、y轴的一阶、二阶图像导数，即

式中：Gx和Gxx分别为尺度归一化的沿x轴的一阶、二阶高斯导数；Gy和Gyy分别为尺度归一化的沿y轴的一阶、二阶高斯导数；*为卷积。

图像I在滤波器所有方向上一阶、二阶响应的极值［4］，即一阶响应的最大值为

二阶响应的最大值和最小值分别为

这些值经过滤波后得到的微分信息不会随图像的旋转而改变，因而具有旋转不变性。

1.2 6 种微分结构特征

基于得到的图像微分最大值和最小值，构建了6种对线性灰度反转变化具有鲁棒性的特征。

（1）局部二阶曲率的形状指数

（2）图像微分结构信息的混合极值比

（3）一阶图像微分梯度幅值的最大值

（4）二阶图像微分极值的最大最小值差分

（5）Log滤波特征

（6）二阶导数不变量

其中，Log滤波特征log，由式（3）相互加后取绝对值得到。二阶导数不变量c由式（7）和（8）求平方和推导得到。根据可控滤波理论［5］，基于式（2）、（3）的特征具有旋转不变性，进一步对其进行线性和非线性变换或者组合后得到的特征log、c 仍具有旋转不变性。

根据实验测试，以上6 种特征具有互补性，当对其联合编码后，可有效提高图像在旋转和灰度反转下的分类精度。

1.3 多尺度联合编码

在进行联合编码之前，采用高斯滤波器σ ＝1、σ ＝2 和σ ＝3 尺度对图像进行滤波，σ 的不同取值对图像进行不同程度的平滑，取值越大平滑效果越好。得到6 种带有图像微分结构信息的特征后，对其进行基于主导思想的联合编码［10］。

图像线性灰度变化的数学模型为

式中：Y为变换后的图像灰度矩阵；X为变换前的图像灰度矩阵；l、h分别为当图像灰度反转时像素点对比度及亮度的变化，h可以通过加减和微分消去，但是l带来的变化会进一步保留，并且l的正负变化会给编码带来极大干扰。针对这个问题，采用主导编码克服l变化所带来灰度值的正负变化。

受SLGP的主导强度顺序度量［10］的启发，在主导编码中，首先对整幅图像求取一个均值t，再与所有像素点的值进行比较。图像中值大于t的像素点数量

式中：n为像素点的数量；pi为像素点的值。则可定义另一个量m2＝n-m1为值小于或等于t的像素点的数量。定义第i个像素点的编码表达式为：

式中：Pi为第i个像素；φm1为图像中值大于t的像素的集合，属于φm1的像素编码为1，否则编码为0。大于t的像素的数量不会随l符号的改变而改变。因此，主导编码具有灰度反转不变性。

图1所示为生成GIRIH方法的主体框架，其利用一种滤波图像可以得到6 位比特中的一位，编码方法采用主导思想编码，得到不变特征GIRIH。

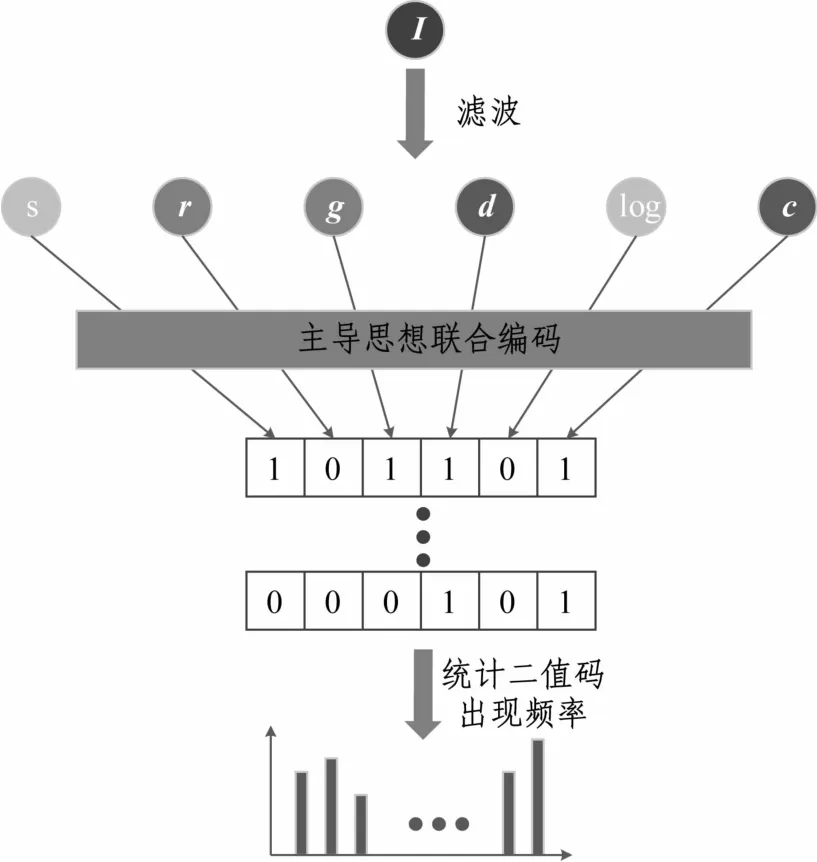
图1 生成GIRIH的方法主体框架

高斯导数滤波已用于提取有效的纹理特征，如LETRIST［5］，但这些特征本身对于光照反转通常比较敏感。为此，需要对具有判别力的特征作进一步处理，如取绝对值，构造出新的特征二阶导数不变量，以及基于主导思想的二值量化和联合编码，实现一种对光照反转具有鲁棒性的特征提取方法。

2 实验结果与分析

本文采用Intel i7-7700 和8 GB 内存的PC 和Matlab 2019a 作为实验工具，用Outex［1］、CUReT［12］及KTH-TIPS［13］3 个基准数据库验证GIRIH 特征的有效性。对比LBP［1］、 LTP［2］、 CLBP［3］、 CLBC［4］、LETRIST［5］、JCLSFP［6］、GLBP［7］、LGP［8］、NRLBP［9］、SLGP［10］、LGIOP［11］共11 种纹理特征提取方法。

2.1 数据集划分方法

对于Outex数据库，选用TC10 和TC12 两个子库进行实验，使用其自带的训练集与测试集文件进行实验，TC10 子库本身含有旋转变化，用来测试旋转不变性，TC12 子库含有光照变化，用来测试光照不变性。CUReT数据库包含61 类纹理，每类有92 幅图像，从每类中随机选取46 幅图像作为训练集，其余的图像作为测试集。KTH-TIPS 数据库包含10 类纹理，每类有81幅图像，从每类中随机选取40 幅图像作为训练集，其余作为测试集。CUReT和KTH-TIPS数据库没有固定的训练集和测试集划分，因此，需要进行多次分类实验，计算平均的分类精度。

2.2 灰度反转与分类方法

实验中，将所有图像转换为灰度图像，并将灰度值限制在［0，255］。对于线性灰度反转模型，对待分类的测试图像执行线性变化I'＝-I+255；对于非线性模型，对待分类的测试图像执行非线性变化I'＝+255。

采用卡方距离作为图像分类的标准，其表达式为

式中：A为训练集图像生产的特征向量；T为测试集图像生成的特征向量。取卡方距离最小的类别为测试图像所属的类别。

2.3 与其他算法比较

考虑GIRIH特征具有灰度反转不变性，在对比其他方法时对使用的数据集进行了灰度反转处理。表1对比了不同方法在线性灰度反转的数据集上的分类精度。LBP等变体描述符的参数含有半径，实验中半径取值为1、2、3 以及3 种半径联合条件下，对LBP、LTP、CLBP、LGP、GLBP和NRLBP分别进行实验，取这些描述符在4 种条件下性能最好的数据与GIRIH 方法的数据进行对比。

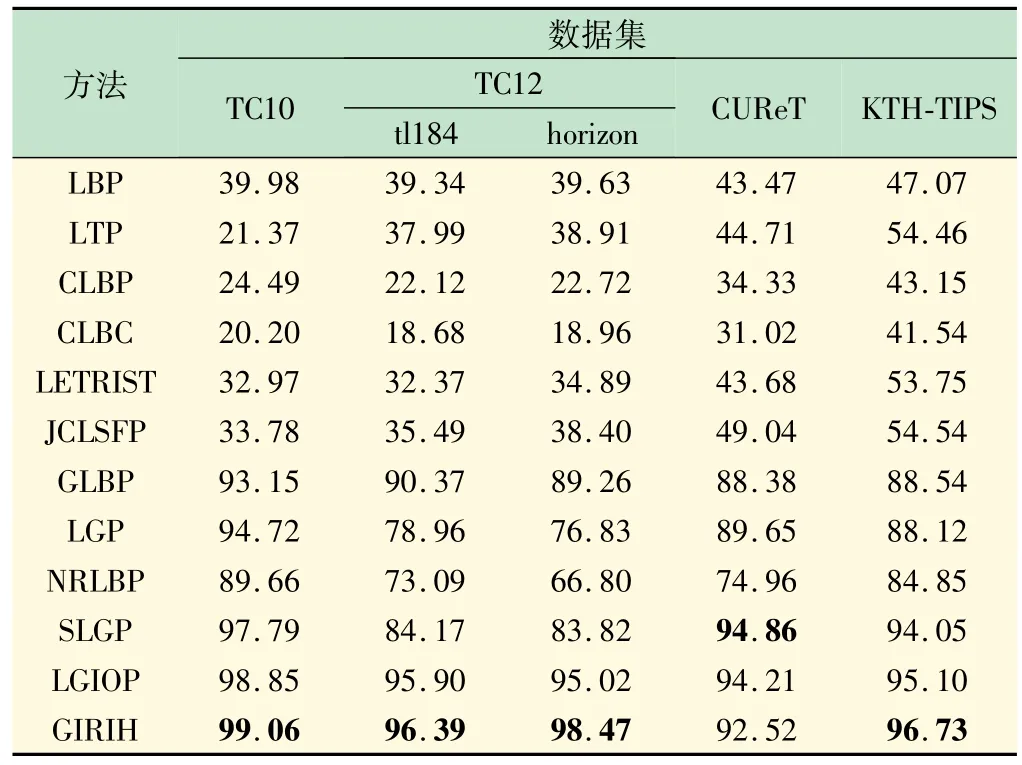
表1 当σ ＝1、2 和3 时多尺度GIRIH与其他方法在线性灰度反转下的分类精度%

由表1 可见，灰度的反转变化会使基于传统LBP的描述符的分类性能急剧下降。原因在于灰度值的巨大变化会影响近邻像素与中心像素间的灰度差分，从而使基于灰度差分生成的二值码与原图像的二值码不再相同。在用直方图进行对比时，图像与原本所属类的距离就会变大，最终造成图像分类错误。NRLBP特征本身没有旋转不变性方法，分类性能均不理想，LTP、GLBP和SLGP采用LBP标准模式具有旋转不变性，总体分类性能有较大提升。其中GLBP 在含有光照变化的TC12 中效果更佳，SLGP在本身含有旋转变化的TC1O中效果更佳。LGIOP与GIRIH特征本身均具有旋转与反转不变性，综合分类性能更优。所提GIRIH方法在本身含有旋转变化的TC10 数据库与含有光照变化的TC12 数据库皆有更高的分类性能，说明GIRIH的特征能有效抵抗图像旋转和光照带来的变化。

图2 所示为几种典型直方图比较。本文选择Outex数据库TC10 子库本身45°旋转图片做线性反转［见图2（a）］，同与其卡方距离最近的图片进行直方图对比。由图2（b）～（e）可见，LBP直方图之间距离较大，造成图像分类错误，NRLBP 直方图之间也存在一定距离，分类正确，但卡方距离最近图片的灰度及纹理不及GLBP 准确。GLBP、SLGP 直方图之间距离较小，性能更优。由图2（d）～（f）可见，GIRIH直方图之间距离比SLGP小，编码数量比GLBP 更多，因此包含的纹理信息更加准确丰富，性能更优。

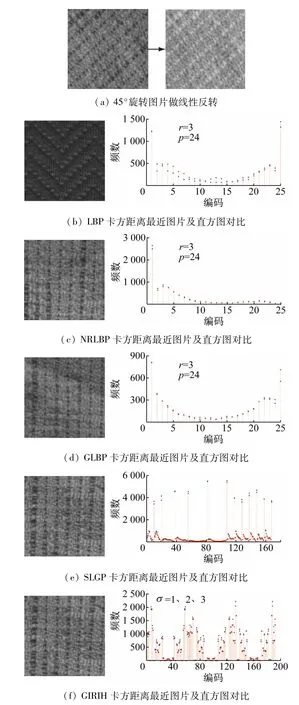
图2 几种典型直方图比较

表2 对非线性光照变化也进行了验证，对比表1和2 中GIRIH的性能，GIRIH 在各数据库下性能的下滑并没有其他方法严重，说明GIRIH 对非线性光照变化也具有一定的鲁棒性。

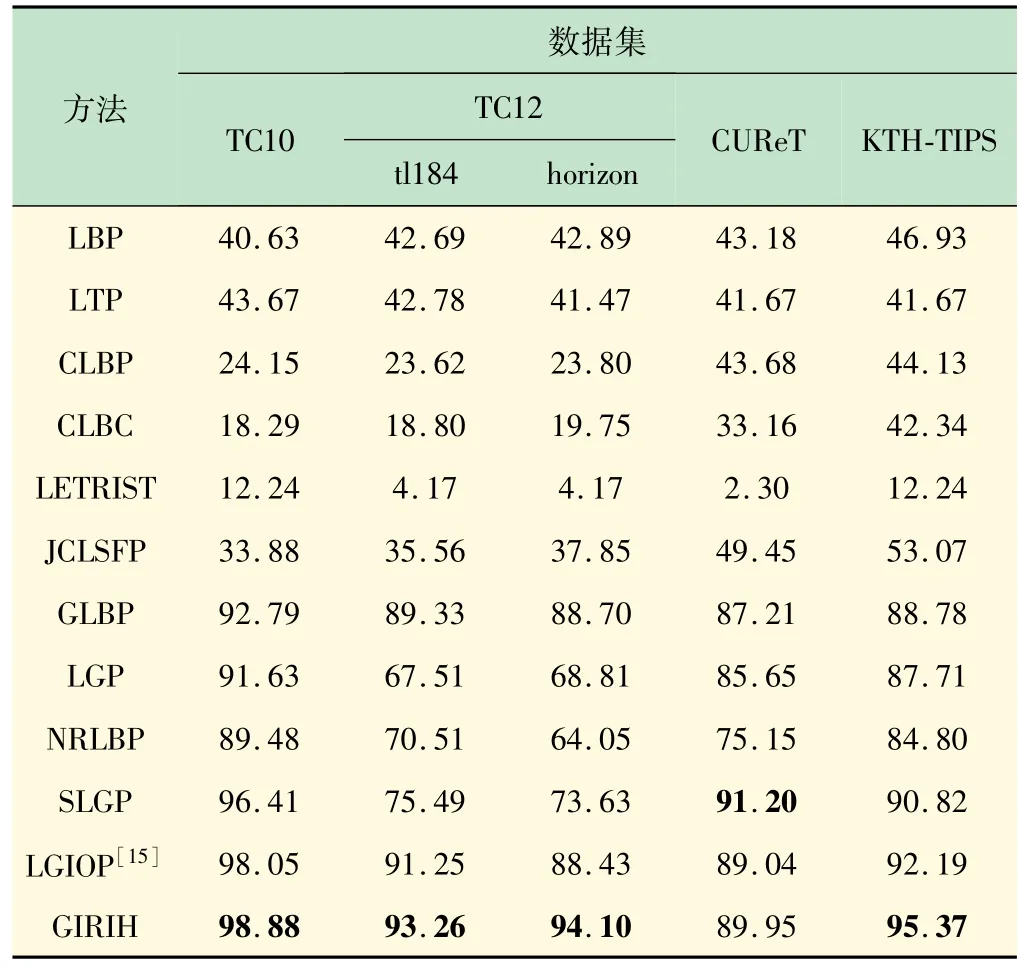
表2 当σ ＝1、2 和3 时多尺度GIRIH与其他方法在非线性灰度反转下的分类精度%

2.4 尺度分析

GIRIH特征在线性和非线性灰度反转条件下都能取得不错的分类性能（见表1 和2），其中GIRIH 的尺度σ取1、2、3 多尺度联合。实验测试了尺度对GIRIH性能的影响，可以看到单尺度下σ ＝2 的性能最好，随着尺度的变大GIRIH 的性能有所下降，对于联合尺度，联合的尺度越多性能越好。但是当联合到σ ＝4时，GIRIH的性能提升不大，且在有些数据库下的性能有所下降。因此，在与其他方法对比时，采用σ 取1、2、3 的多尺度GIRIH，不同尺度GIRIH 在线性灰度反转下的分类精度如表3 所示。

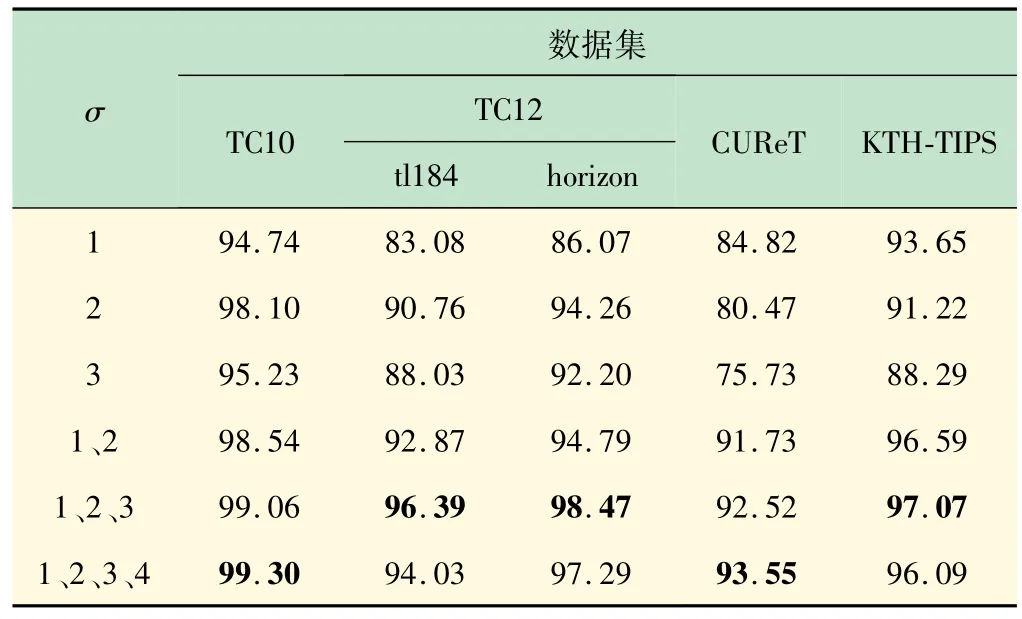
表3 不同尺度GIRIH在线性灰度反转下的分类精度%

2.5 特征有效性分析

采用了6 种图像微分特征，为验证每种特征的有效性，对特征进行线性叠加实验，在实验中，GIRIH 的尺度σ取1 和2 两种尺度联合。当σ ＝1 和2 时，多尺度GIRIH中的多种特征在线性灰度反转下的分类精度如表4 所示。

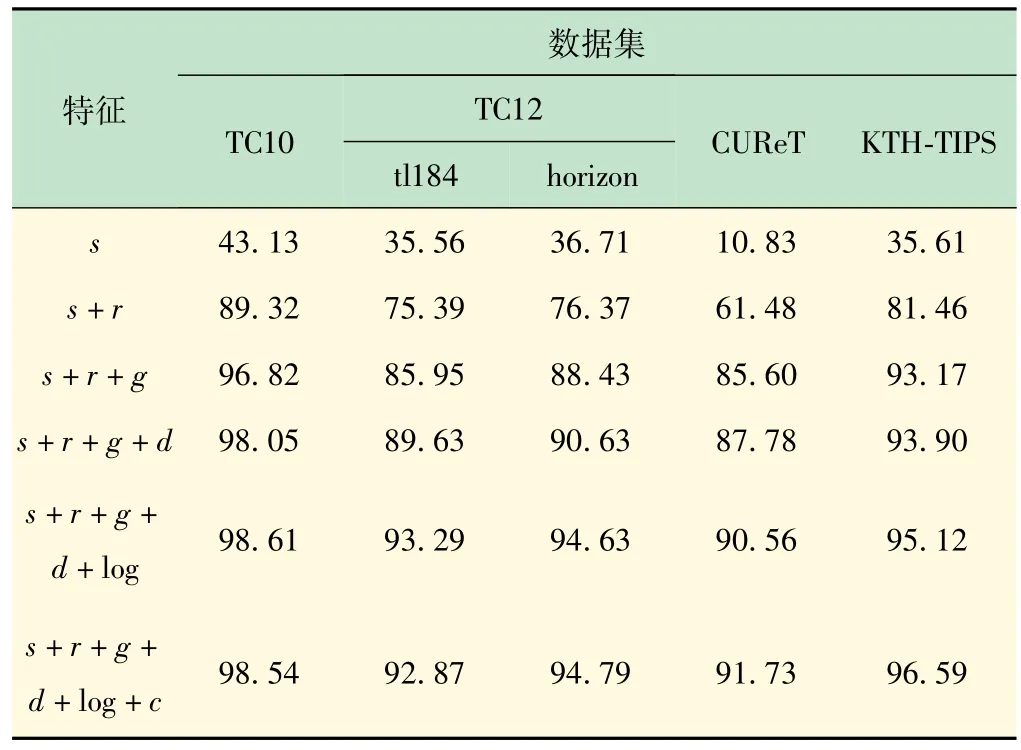
表4 当σ ＝1 和2 时多尺度GIRIH中多种特征在线性灰度反转下的分类精度%

由表4 可见，随着一种新特征的加入，GIRIH在所有数据库的性能都有所提升，其在GIRIH 性能较低时尤其明显。随着特征达到5 种以上时，GIRIH 的性能提升不再明显，且有些数据库下的性能出现了轻微的下降，说明GIRIH 的特征开始出现了冗余。因此，最终选择了6 种特征作为GIRIH 的底层特征。实验表明，GIRIH在旋转及光照变化下的分类任务中表现良好。

2.6 算法复杂度分析

针对所提算法，图像特征计算的时间复杂度可表示为

式中：w与z表示图片的长与宽；常数C1、C2和C3分别表示用3 种尺度的滤波核计算一个像素的时间；常数C4表示对一种特征进行主导编码的时间；k是特征数；b为计算6 种特征的时间。

选择数据库Outex TC_10 和KTH_TIPS aluminium各一张图片如图3 所示，运行不同算法，所需运行时间如表5 所示。

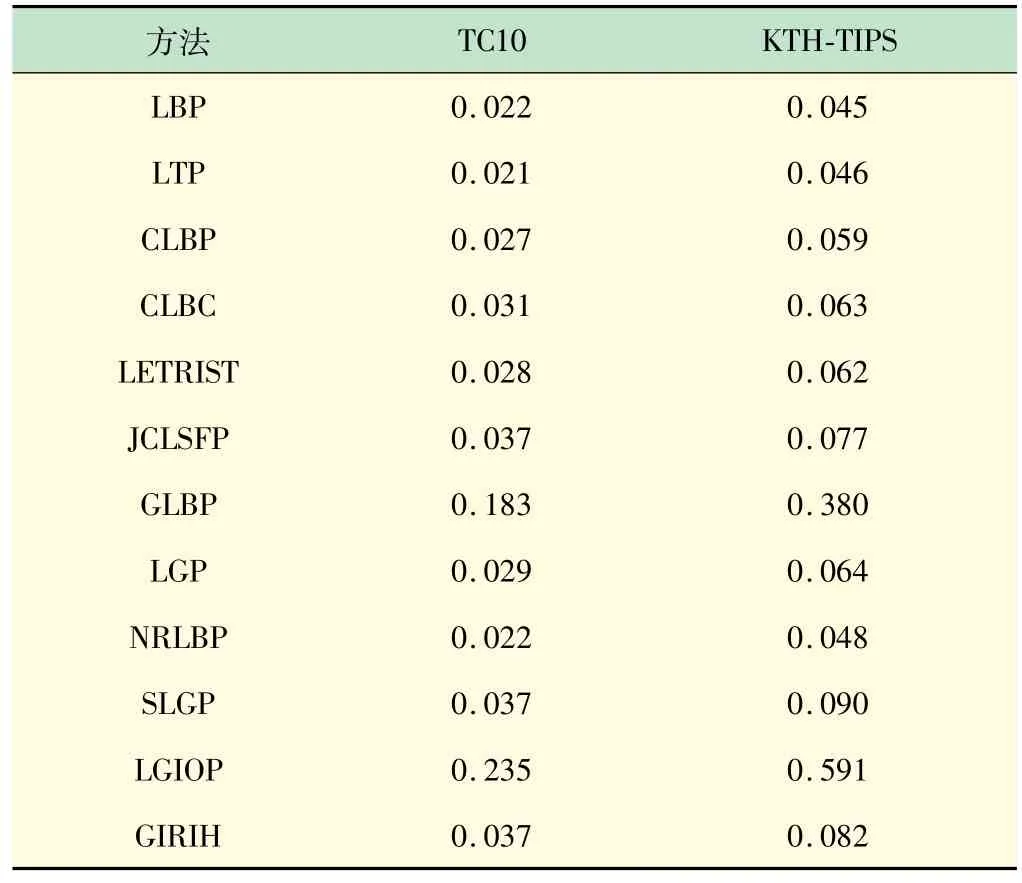
表5 不同方法提取单张图片所需时间s

图3 选择数据库的图片

由表5 可见，LGIOP 运行时间最长，LBP、LTP 和NRLBP运行时间比较短。所提的GIRIH 运行时间中等，而其分类精度整体最好。

3 结语

针对传统局部二值模式及其派生的纹理描述符分类性能明显下降的问题，提出了一种GIRIH 特征表示方法。通过对3 个纹理图片数据库进行光照反转与旋转分类实验测试，结果表明，所提的GIRIH 方法能有效改善灰度反转问题；并对图像的旋转变化具有一定的鲁棒性。进一步，所构造的6 种特征还存在冗余的信息，可以进一步优化；同时，6 种特征并没有完全利用图像信息，还可以增加新的特征继续进行实验。